基于多卡GPU的随机炮分配相位编码全波形反演

宋　鹏,王修田

(1.中国海洋大学海洋地球科学学院,山东青岛266100;2.青岛国家海洋科学与技术实验室,山东青岛266100;3.海底科学与探测技术教育部重点实验室,山东青岛266100)



基于多卡GPU的随机炮分配相位编码全波形反演

宋鹏1,2,3,王修田1,2,3

(1.中国海洋大学海洋地球科学学院,山东青岛266100;2.青岛国家海洋科学与技术实验室,山东青岛266100;3.海底科学与探测技术教育部重点实验室,山东青岛266100)

摘要:针对传统时间域相位编码全波形反演的炮间串扰问题,提出了一种基于随机炮分配的相位编码时间域全波形反演策略,并实现了基于多卡GPU的加速。基于四卡GPU加速的模型反演实验表明：在GPU和相位编码技术的共同加速下,时间域全波形反演的计算效率可得到显著提升,同时由于各卡间的随机炮分配,基于随机炮分配的相位编码时间域全波形反演策略能更有效地压制串扰噪声,因此其比传统的相位编码全波形反演具有更高的反演精度和收敛效率。

关键词：全波形反演;相位编码;串扰;多卡GPU

时间域全波形反演方法由TARANTOLA首先提出[1-2],其基于波动方程理论,充分利用实测地震记录的整体信息(走时、振幅、相位等)来重建地下介质速度结构。对于理想观测系统,理论上全波形反演的分辨率可达到波长数量级[3-5]。

近20年来,时间域全波形反演方法获得了长足的发展。BUNKS等[6]提出了时间域的多尺度全波形反演策略,有效避免了局部极值,提高了全波形反演的精度和稳定性；MAO等[7]和ZHANG等[8]采用边界存储策略显著降低了全波形反演的内存消耗；BROSSIER等[9]、张生强等[10]以及苗永康[11]实现了基于L-BFGS算法的全波形反演；WANG等[12]提出并实现了基于混合迭代优化方法的全波形反演,大大提高了反演的收敛效率和深部地层的反演精度；ZHANG等[13-14]提出了一种基于地震波能量的梯度预处理方法,其应用声波方程模拟的波场信息对梯度进行预处理,可在有效提高深层反演精度的同时避开Hessian矩阵或其逆矩阵的计算和存储。针对由于低频缺失而导致的反演初始模型难以获得的问题,WU等[15]提出了一种基于地震包络的反演方法,其应用地震数据的包络替代低频信息来反演速度模型的长波长结构,为全波形反演提供了一个较为精确的初始模型。

时间域全波形反演技术已逐渐由理论模型研究向实际数据应用方向发展,然而超大计算量制约了该技术在实际生产中的广泛应用。针对全波形反演的大计算量问题,DIAZ等[16]提出了一种基于随机炮抽取的时间域全波形反演策略,在每次迭代时仅随机抽取部分炮参与反演,而不是让全部炮集参与计算;HA等[17]提出了一种基于循环炮采样的时间域全波形反演,同样在每次迭代时不对所有炮进行反演计算,而是通过循环采样模式选取部分炮参与反演。以上两种方法均减少了每次迭代时参与计算的炮数,能够在一定程度上提高反演的计算效率,但其显然仅能适应于覆盖次数较高的观测系统,且难以从根本上解决全波形反演的大计算量问题。2009年,KREBS等[18]基于多炮同时反演的思想,提出了一种基于相位编码技术的多炮同时反演方法(以下简称为相位编码全波形反演),将所有炮的震源褶积上一个随机产生的相位编码函数,生成一个超级震源,并应用相同的编码函数对实际地震记录进行褶积,生成超级炮集记录,这样对于所有炮的反演计算即可转换成对一个超级炮集记录进行反演,大幅度提高了全波形反演的计算效率(计算效率约可提高炮数倍)。但相位编码全波形反演在提高计算效率的同时,也由于多炮的同时反演(即仅对一个超级炮集记录进行反演)而产生大量的炮间串扰噪声,从而影响整个全波形反演的计算精度和收敛效率。

GPU凭借其优异的浮点运算能力和更快的访存速度已成为新一代的高性能计算工具。为方便开发者编程以实现算法的GPU加速,NVIDIA公司于2007年推出了统一计算设备架构(CUDA)平台,大大简化了基于GPU的算法研发过程。自CUDA推出后,GPU的高性能计算在地球物理界得到广泛应用[19-21],并且目前已有学者对于时间域全波形反演的GPU加速进行了研究和探讨[7,22-23],其研究成果表明,即使是采用单卡GPU,时间域全波形反演也能获得几十倍的加速比;而当前多卡GPU集群系统已逐渐普及,因此发展基于多卡GPU的全波形反演算法,以借助于多卡GPU集群的高性能并行计算能力来提高全波形反演的计算效率将是未来的发展趋势。

本文提出了一种基于多卡GPU的随机炮分配相位编码时间域全波形反演策略,在每次迭代时，首先根据GPU的卡数将所有炮随机分成若干组,再将每组炮进行相位编码形成独立的超级炮集参与反演计算,最后将各个独立超级炮集的计算结果合成总梯度和总目标函数。实验表明,这种对随机生成的多个独立超级炮集的反演技术可有效压制炮间串扰的影响,提高迭代精度和收敛效率;同时在GPU和相位编码技术的共同加速下,时间域全波形反演的计算效率也得到大幅度提升。

1基于随机炮分配的相位编码全波形反演

1.1随机炮分配相位编码全波形反演目标函数

设在一个计算平台中能够应用的GPU卡数为M,随机分配到第m个卡(组)的炮集数为Nm,则最小平方意义下的随机炮分配相位编码全波形反演的目标函数可写为：

(1)

式中：c表示速度模型;sn为第m组中第n炮的震源子波;p为相应的合成地震记录;dn表示第m组中第n炮的观测地震记录;en表示第m组中第n炮的编码函数序列(其与常规的相位编码序列[18]类似,为保证各组中的炮间串扰得到有效压制,en需随机给出,一般情况下,当j≠k时,ej≠ek);“⊗”表示褶积。

当p(c,sn)是震源的线性函数时,(1)式可写为：

(2)

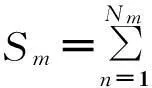
由(2)式可知,基于随机炮分配的相位编码全波形反演将所有炮的反演计算转换成由随机分配形成的M个超级震源与M个超级记录的反演,通过随机炮的分配减少了参与编码的实际炮数,降低了串扰产生的几率,如果在每次迭代时均重新随机分配各组中的炮号(数)则还能避免相同的串扰作用于每次迭代中,因此基于随机炮分配的相位编码全波形反演比传统的相位编码全波形反演有更高的反演精度和收敛效率。显然,当M=1时(即所有炮仅为1组),基于随机炮分配的相位编码全波形反演即转化为常规的相位编码全波形反演。

1.2随机炮分配相位编码全波形反演实现步骤

基于多卡GPU的随机炮分配相位编码全波形反演的具体实现步骤如下。

1) 根据GPU卡数将所有炮随机分为若干组(每次迭代时均重新随机分配各卡对应的炮号(数))。

2) 将每组炮分别与一个随机的编码函数序列褶积,生成若干个超级炮集,并将其对应的震源子波分别与相同的编码函数序列褶积,生成若干个超级震源。

3) 在每一个GPU卡上,分别以一个超级震源作为正时扰动进行正演模拟得到正时波场u(x,t,Si)(这里x表示空间坐标,t表示时间,i表示卡号)和模拟记录,并进一步得到目标函数和超级记录残差,然后以该超级记录残差作为逆时扰动计算得到逆时波场ψ(x,t,Si),并按(3)式计算得出各个超级记录对应的梯度值：

(3)

式中：di表示第i个GPU卡计算得到的梯度;c(x)表示速度模型;“·”表示时间的一阶微分;T表示最大时间。

4) 将各个GPU卡计算得出的梯度值合成总梯度同时得到总目标函数,并进一步计算得到迭代步长,然后修改模型,即完成本次迭代。

5) 重复步骤1)到步骤4),直到目标函数满足要求或达到最大迭代次数。

基于多卡GPU的随机炮分配相位编码全波形反演的具体反演流程见图1(以四卡为例)。

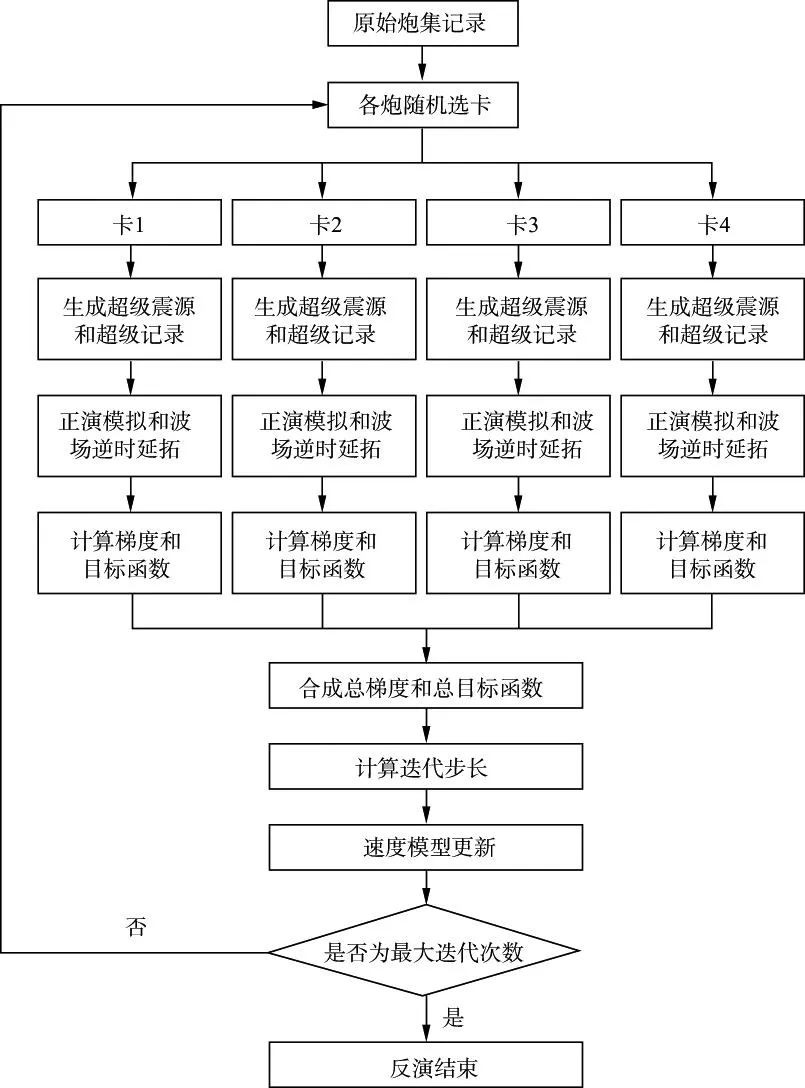
图1　基于四卡GPU的随机炮分配相位编码反演流程

2相位编码全波形反演的GPU加速

本文首先基于消息传递接口(MPI),根据卡数启动相应数目的进程,并将每个进程与对应的GPU卡绑定;而在每个GPU卡内则基于CUDA,实现相位编码全波形反演的GPU加速,这样基于多卡GPU的随机炮分配相位编码全波形反演的计算效率与基于单卡加速的传统相位编码全波形反演相当。

基于CUDA进行编程时,CPU作为主机,GPU被视作设备。主机上运行的函数称为主机函数,设备上运行的函数称为内核函数。主机函数负责串行部分,并负责将数据由内存复制到显存中以供GPU使用。内核函数负责执行高度线程化的并行处理任务,并以线程网格(grid)的形式组织。每个线程网格又可分为若干个线程块(block),每个线程块包含若干个线程(thread)。通过这样的组织形式,内核函数可同时启动成千上万个线程。内核函数执行完毕后需将处理完的数据由显存复制到内存中。

本文根据相位编码时间域全波形反演的计算模式和CUDA特点,创建了相关的主机函数和核函数(具体名称和功能见表1,其中核函数前缀为“__global__”),实现了相位编码全波形反演的GPU加速。

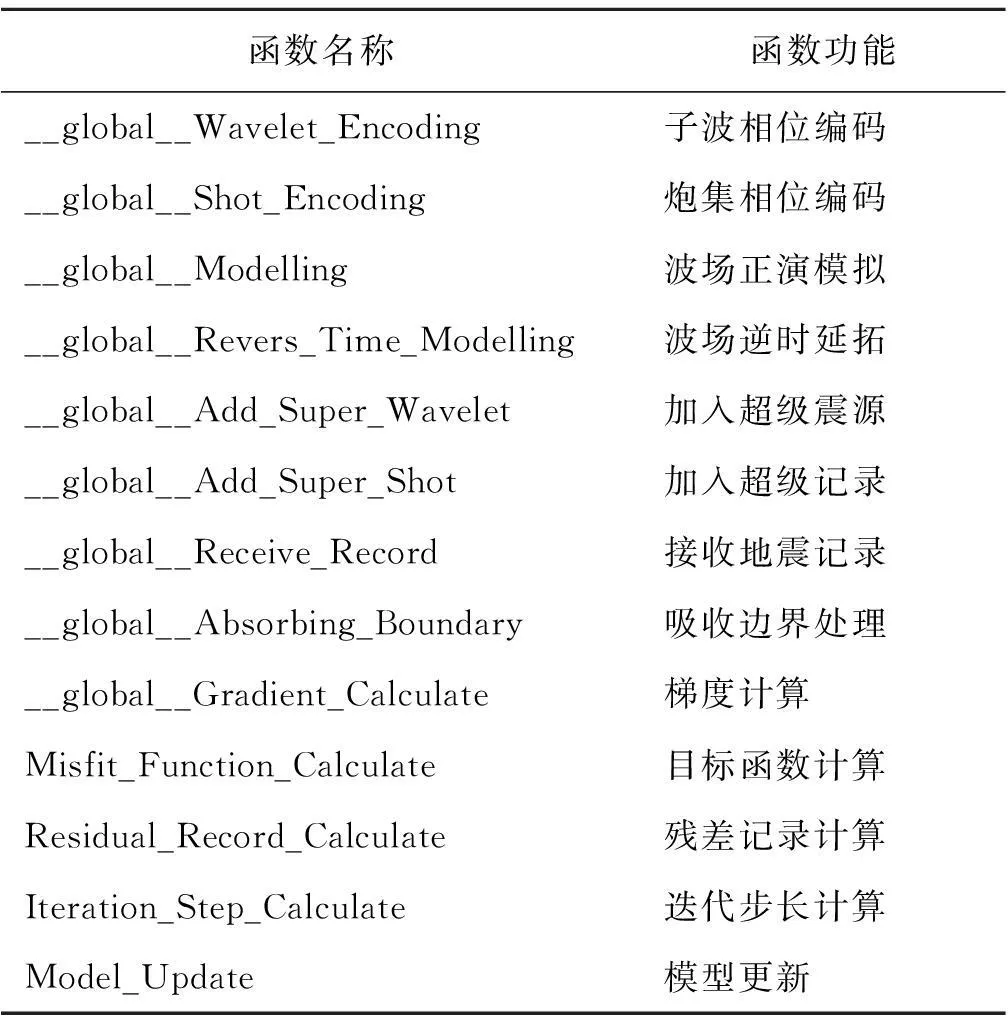
表1　主机函数及核函数

应用表1中的函数,基于CUDA的相位编码时间域全波形反演的一段伪码如图2所示。其中,“P”为内存中的波场数组,“P_GPU”为显存中的波场数组,“V”为内存中的模型数组,“V_GPU”为显存中的模型数组,“=>”表示由内存复制到显存,“<=”表示由显存复制到内存。

图2　基于CUDA的相位编码全波形反演伪码

3模型反演效果分析

3.1层状断块速度模型反演效果分析

层状断块速度模型见图3,该模型横向距离为6000m,深度为1800m,共5层,其速度从上到下依次为2700,3200,3900,5000,5500m/s。基于该模型建立道固定、炮移动的观测系统,炮间距为25m,共241炮,道间距也为25m,共241道。

本文基于BUNKS等[6]提出的多尺度分频反演策略,共分5个频段(高截频分别为5.0,9.0,16.3,29.6,50.0Hz)进行反演,每个频段各25次迭代,初始速度模型如图4所示。

基于一个含4个卡的GPU工作站测试反演计算效率(GPU型号为NVIDIA Tesla K20)。测试结果显示,基于单卡的传统相位编码反演(以下简称单卡反演)和基于四卡的随机炮分配相位编码反演(以下简称四卡反演)的单次迭代时间均仅为6.5s。

图5为原始炮集记录和超级炮记录(包括单卡反演第1次迭代时合成的超级记录、四卡反演时第1个卡第1次和第2次迭代时所合成的超级记录);单卡反演和四卡反演每个频带各25次迭代的反演结果分别见图6和图7。

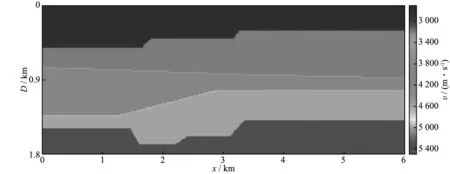
图3　层状断块速度模型

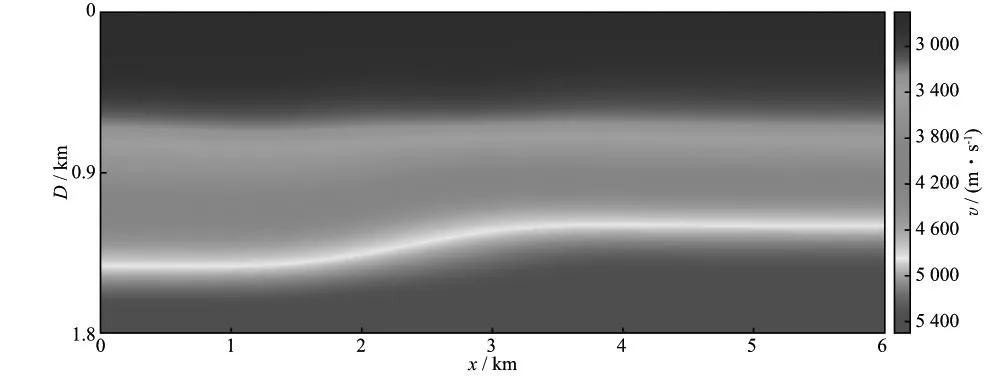
图4　层状断块初始速度模型

图5　原始炮集记录及超级炮记录a 原始单炮记录(炮号=120); b 单卡反演第1次迭代时的超级记录; c 四卡反演中第1个卡第1次迭代时的超级记录;d 四卡反演中第1个卡第2次迭代时的超级记录

由图5可知,四卡反演时每卡参与编码的炮数要远远小于单卡反演,且每次迭代所参与编码的炮都为随机产生,这最大限度地降低了炮间串扰对于反演的影响。对比图6和图7可知,在同样迭代次数下,四卡反演的精度明显高于单卡反演,串扰噪声大幅减少。

3.2逆掩断层二维模型反演效果分析

图6　层状断块速度模型单卡25次迭代反演结果

图7　层状断块速度模型四卡25次迭代反演结果

图8　逆掩断层二维速度模型

本文采用的逆掩断层二维模型(图8)长度为10km,深为2.325km,横、纵向网格步长均为12.5m。设计接收道固定、炮移动的观测方式,每炮接收道相同,自左向右等间隔排放,共401道,道间距为25m,检波点深度为25m;炮间距也为25m,炮点深度为25m,共401炮。基于BUNKS等[6]提出的多尺度分频反演策略和图9所示的初始模型分4个频段(高截频分别为5.0,11.0,23.7和47.5Hz)进行反演,每个频段各25次迭代。此外,还采用了ZHANG等[14]提出的基于地震波能量的梯度预处理方法以提高深层的反演精度。

反演同样基于型号为Tesla K20的四卡GPU工作站,单卡与四卡反演的单次迭代时间均仅为13s。

图9　逆掩断层二维初始速度模型

图10　逆掩断层二维速度模型单卡25次迭代反演结果

图11　逆掩断层二维速度模型四卡25次迭代反演结果

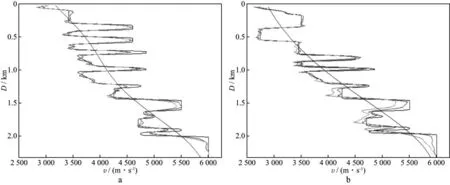
图12　逆掩断层二维速度模型在x=4000m(a)与x=6525m(b)处25次迭代反演速度曲线(黑线代表真实速度,蓝线代表初始模型速度,绿线代表单卡反演结果,红线代表四卡反演结果)

图10和图11分别为单卡反演和四卡反演每频带各25次迭代的反演结果;图12为水平方向4000和6525m处单卡和四卡反演的速度曲线。对比图10和图11以及图12中单卡和四卡反演的速度曲线可知,25次迭代后四卡反演的结果明显优于单卡反演结果。

图13　逆掩断层二维速度模型单卡50次迭代反演结果

图14　逆掩断层二维速度模型四卡50次迭代反演结果

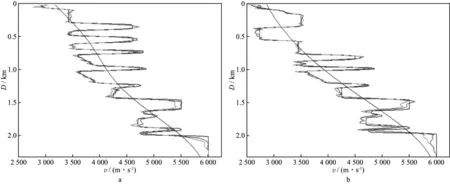
图15　逆掩断层二维速度模型在x=4000m(a)与x=6525m(b)处50次迭代反演速度曲线(黑线代表真实速度,蓝线代表初始模型速度,绿线代表单卡反演结果,红线代表四卡反演结果)

图13和图14分别为单卡反演和四卡反演每频段各50次迭代后的反演结果;图15为4000m和6525m处的反演速度曲线。对比图13和图14以及图15中的单卡和四卡反演速度曲线可知,50次迭代后四卡反演的精度也明显高于单卡反演结果。

本文应用BEN-HADJ-ALI等[24]定义的一个反演精度评估因子来评估反演结果和真实模型的误差,反演精度评估因子的表达式为：

(4)

式中：mresult表示最终反演结果;mreal表示真实速度。根据(4)式计算得到单卡反演25次迭代、四卡反演25次迭代、单卡反演50次迭代以及四卡反演50次迭代的Eres值见表2。

表2　逆掩断层二维模型反演结果的Eres值

由表2可知,对于相同的迭代次数,四卡反演的精度总是高于单卡反演,甚至四卡25次迭代的反演精度都要高于单卡50次迭代的反演结果,因此逆掩断层二维模型基于四卡GPU的随机炮分配相位编码反演的收敛效率和反演精度都远远超过单卡相位编码反演。

4结论与展望

本文提出并实现了基于多卡GPU的随机炮分配相位编码全波形反演,理论分析和模型实验得出如下结论：

1) 基于多卡GPU的随机炮分配相位编码全波形反演可通过卡间随机炮的选取进一步压制炮间的串扰,从而获得更高的反演精度和收敛效率。理论上讲,所用的GPU卡数目越多,对炮间串扰的压制效果越好,相应的反演精度和收敛效率越高。

2) 基于多卡GPU的随机炮分配相位编码全波形反演在相位编码技术的基础上,借助于多卡GPU的加速能力,大幅度提高时间域全波形反演的计算效率。

显然,当GPU卡数达到实际炮数时,随机炮分配相位编码全波形反演即转化为通常意义下的全波形反演,此时各卡仅处理其中一个炮集数据,也就不存在炮间串扰问题。但在当前(甚至今后相当长的一段时间内)的计算环境下,海量的地震数据使得“GPU卡数等于实际炮数”的条件在实际生产应用中很难满足。因此,基于多卡GPU的随机炮分配相位编码全波形反演不失为一种较为理想的能适合于大规模数据的反演策略。

参考文献

[1]TARANTOLA A.Inversion of seismic reflection data in the acoustic approximation[J].Geophysics,1984,49(8):1259-1266

[2]TARANTOLA A.A strategy for nonlinear elastic inversion of seismic reflection data[J].Geophysics,1986,51(10):1893-1903

[3]WU R S,TOKSOZ M N.Diffraction tomography and multisource holography applied to seismic imaging[J].Geophysics,1987,52(1):11-25

[4]PRATT R G,SHIPP R M.Seismic waveform inversion in the frequency domain.part2:fault delineation in sediments using crosshole data[J].Geophysics,1999,64(3):902-914

[5]卞爱飞,於文辉,周华伟.频率域全波形反演方法研究进展[J].地球物理学进展,2010,25(3):982-993

BIAN A F,YU W H,ZHOU H W.Progress in the frequency-domain full waveform inversion method[J].Progress in Geophysics,2010,25(3):982-993

[6]BUNKS C,SALECK F M,ZALESKI S,et al.Multiscale seismic waveform inversion[J].Geophysics,1995,60(5):1457-1473

[7]MAO J,Wu R S,Wang B L.Multiscale full waveform inversion using GPU[J].Expanded Abstracts of 82ndAnnual Internat SEG Mtg,2012:1-7

[8]ZHANG Q C,ZHOU H,WANG J.Efficient boundary storage strategy for three-dimensional elastic full-waveform inversion in time domain[J].Expanded Abstracts of 84thAnnual Internat SEG Mtg,2014:1142-1146

[9]BROSSIER R,OPERTO S,VIRIEUX J.Seismic imaging of complex onshore structures by 2D elastic frequency-domain full-waveform inversion[J].Geophysics,2009,74(6):WCC105-WCC118

[10]张生强,刘春成,韩立国,等.基于L-BFGS算法和同时激发震源的频率多尺度全波形反演[J].吉林大学学报(地球科学版),2013,43(3):1004-1012

ZHANG S Q,LIU C C,HAN L G,et al.Frequency multi-scale full waveform inversion based on L-BFGS algorithm simultaneous sources approach[J].Journal of Jilin University(Earth Science Edition),2013,43(3):1004-1012

[11]苗永康.基于L-BFGS算法的时间域全波形反演[J].石油地球物理勘探,2015,50(3):469-474

MIAO Y K.The time-domain full waveform inversion based on L-BFGS algorithm[J].Oil Geophysical Prospecting,2015,50(3):469-474

[12]WANG Y,DONG L G,LIU Y Z.Improved hybrid iterative optimization method for seismic full waveform inversion[J].Applied Geophysics,2013,10(3):265-277

[13]ZHANG Z G,LIN Y Z,HUANG L J.Full-waveform inversion in the time domain with an energy-weighted gradient[J].Expanded Abstracts of 81stAnnual Internat SEG Mtg,2011:2772-2776

[14]ZHANG Z G,HUANG L J,LIN Y Z.A wave-energy-based precondition approach to full-waveform inversion in the time domain[J].Expanded Abstracts of 82ndAnnual Internat SEG Mtg,2012:1-5

[15]WU R S,LUO J R,WU B Y.Seismic envelope inversion and modulation signal model[J].Geophysics,2014,79(3):WA13-WA24

[16]DIAZ E,GUITTON A.Fast full waveform inversion with random shot decimation[J].Expanded Abstracts of 81stAnnual Internat SEG Mtg,2011:2804-2808

[17]HA W,SHIN C.Efficient full waveform inversion using a cyclic shot sampling method[J].Expanded Abstracts of 82ndAnnual Internat SEG Mtg,2012:1-6

[18]KREBS J R,ANDERSON J E,HINKLEY D,et al.Fast full-wavefield seismic inversion using encoded sources[J].Geophysics,2009,74(6):WCC177-WCC188

[19]李博,刘国峰,刘洪.地震叠前时间偏移的一种图形处理器提速实现方法[J].地球物理学报,2009,52(1):245-252

LI B,LIU G F,LIU H.A method of using GPU to accelerate seismic pre-stack time migration[J].Chinese Journal of Geophysics,2009,52(1):245-252

[20]刘红伟,李博,刘洪,等.地震叠前逆时偏移高阶有限差分算法及GPU实现[J].地球物理学报,2010,53(7):1725-1733

LIU H W,LI B,LIU H,et al.The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation[J].Chinese Journal of Geophysics,2010,53(7):1725-1733

[21]刘国峰,刘洪,李博,等.山地地震资料叠前时间偏移方法及其GPU实现[J].地球物理学报,2009,52(12):3101-3108

LIU G F,LIU H,LI B,et al.Method of prestack time migration of seismic data of mountainous regions and its GPU implementation[J].Chinese Journal of Geophysics,2009,52(12):3101-3108

[22]WANG B L,GAO J H,ZHANG H L,et al.CUDA-base acceleration of full waveform inversion on GPU[J].Expanded Abstracts of 81stAnnual Internat SEG Mtg,2011:2528-2533

[23]张猛,王华忠,任浩然,等.基于CPU/GPU异构平台的全波形反演及其实用化分析[J].石油物探,2014,53(4):461-467

ZHANG M,WANG H Z,REN H R,et al.Full waveform inversion on the CPU/GPU heterogeneous platform and its application analysis[J].Geophysical Prospecting for Petroleum,2014,53(4):461-467

[24]BEN-HADJ-ALI H,OPERTO S,VINEUX J.An efficient frequency-domain full waveform inversion method using simultaneous encoded sources[J].Geophysics,2011,76(4):R109-R124

(编辑：陈杰)

The phase-encoding full waveform inversion with random shots allocation based on the acceleration of multi-card GPU

SONG Peng1,2,3,WANG Xiutian1,2,3

(1.CollegeofMarineGeo-science,OceanUniversityofChina,Qingdao266100,China;2.QingdaoNationalLaboratoryforMarineScienceandTechnology,Qingdao266100,China;3.KeyLabofSubmarineGeosciencesandProspectingTechniquesMinistryofEducation,Qingdao266100,China)

Abstract:To deal with the crosstalk problem of the traditional time-domain,a strategy of phase-encoded full waveform inversion (FWI) with random shots allocation is proposed and implemented based on the acceleration of multi-card GPU in the paper.Numerical experiments based on a four-card GPU show that,under the acceleration of phase encoding technique and GPU,the computational efficiency of time-domain FWI can be improved greatly.Meanwhile,by the random allocation of shots in each card,this strategy can suppress the crosstalk more effectively.Thus,the time-domain phase-encoding FWI with random shots allocation has higher inversion precision and convergent rate than the traditional method.

Keywords:full waveform inversion,phase-encoding,crosstalk,multi-card GPU

文章编号：1000-1441(2016)02-0251-10

DOI:10.3969/j.issn.1000-1441.2016.02.011

中图分类号：P631

文献标识码：A

基金项目：国家自然科学基金项目(41574105)资助。

作者简介：宋鹏(1979—),男,讲师,主要从事波动方程成像及反演方法研究工作。通讯作者：王修田(1961—),男,教授,主要从事地震数据处理方法研究与软件系统研发工作。

收稿日期：2014-12-05;改回日期：2015-08-15。

This research is financially supported by the National Natural Science Foundation of China (Grant No.41574105).