基于GPU的三维起伏地表单程波叠前深度偏移

段心标,王华忠,白英哲,王立歆,张慧宇,何　英

(1.同济大学海洋与地球科学学院波现象与反演成像研究组,上海 200092;2.中国石油化工股份有限公司石油物探技术研究院,江苏南京 211103)



基于GPU的三维起伏地表单程波叠前深度偏移

段心标1,2,王华忠1,白英哲2,王立歆2,张慧宇2,何英2

(1.同济大学海洋与地球科学学院波现象与反演成像研究组,上海 200092;2.中国石油化工股份有限公司石油物探技术研究院,江苏南京 211103)

摘要:相对于双程波逆时偏移,单程波叠前深度偏移具有计算效率高、高频信息保持好且易于提取成像道集等优势,适用于我国陆上高陡构造不甚发育探区。为满足陆上复杂地表三维探区海量地震数据成像的需求,发展了基于GPU平台的三维起伏地表裂步傅里叶(Split-Step Fourier,SSF)叠前深度偏移技术,并引入了单程波偏移的相位校正技术以及基于分布式炮域成像结果的偏移距域道集并行提取技术。陆上复杂断块及缝洞探区实际资料成像试处理表明：基于GPU的三维起伏地表单程波叠前深度偏移成像方法不仅计算效率高,而且能较为准确地刻画复杂断块及缝洞储集体,在横向变速不太剧烈及陡倾构造不甚发育的探区具有很高的应用价值。

关键词：单程波偏移;共偏移距道集;裂步傅里叶算子;叠前深度偏移

单程波偏移自20世纪60年代以来发展了一系列方法,如裂步傅里叶法(SSF)[1-2]、相移法、相移加内插法(PSPI)、傅里叶有限差分法(FFD)、广义屏法(GSP)等[3-14],成为叠前深度偏移的一个重要分支。与Kirchhoff积分偏移相比,单程波偏移无高频近似假设,能够处理多值走时和焦散问题,在复杂介质成像方面具有较高的精度。与逆时偏移相比,单程波偏移虽然存在陡倾角限制,但具有计算效率高、高频信息保持好、成像道集易于提取等优势。然而,单程波偏移受制于计算量大、高陡构造成像效果不佳等因素,应用范围并不很广,Kirchhoff偏移和逆时偏移则在生产中得到了广泛应用。实际上,我国陆上许多探区高陡构造并不发育,单程波偏移基本能够满足构造成像的需求。

为了提高单程波偏移的计算效率,张兵等[15]基于CUDA语言实现了二维SSF单程波叠前深度偏移,其加速比是CPU(单核)的10倍左右。刘奇琳等[16]结合二维SSF,FFD,GSP等不同单程波偏移的特点设计了不同的GPU算法,并利用Marmousi数据综合比较了不同方法的GPU加速比。LIU等[17]将二维GPU单程波偏移技术拓展到三维情况,并在吉林油田某三维探区应用中获得高分辨率的成像剖面。关于起伏地表单程波偏移,RESHEF[18]提出“逐步外推,逐步累加”法;BEASLEY[19]提出高程静校正加“零速层”偏移法;何英等[20]提出利用波动方程基准面校正数据进行叠前深度偏移的“波场上延”法。其中,“逐步外推,逐步累加”法思路简单,容易实现,并且稳定性好。王成祥等[21]、田文辉等[22]、卢宝坤等[23]分别利用逐步累加波场的思想实现了不同单程波算子的二维起伏地表偏移。然而,截至目前,尚未有公开文献论述三维起伏地表单程波偏移方法。本文基于GPU计算平台,采用直接下延逐步累加波场的思路,实现了三维起伏地表SSF单程波叠前深度偏移，通过起伏地表探区实际资料试处理,验证了方法对复杂断块及缝洞储集体的成像效果。

1SSF叠前深度偏移原理

根据声波介质波动方程,炮点或检波点波场外推表达式为：

(1)

(1)式“±”中,“-”号表示检波点波场向下外推,“+”号表示炮点波场向上外推。下文仅讨论检波点波场向下外推的情况。

对(1)式中的慢度场(速度场的倒数)进行分解,即将每一外推层中的慢度分解为背景慢度和慢度摄动量。在一个外推层内,背景慢度是常数,取其为该层慢度的平均值。

(2)

其中,S0(z)为背景慢度,ΔS(x,y,z)为慢度摄动量。将公式(2)代入外推关系式(1)中,并舍弃慢度摄动的二阶项(要求慢度扰动量比较小),有：

(3)

对(3)式中的第二个根式项作Taylor展开,并整理得:

(4)

(5)

对(5)式进行分裂,得：

(6)

U(ω,x,y,z)]

(7)

式中:Fx,y表示二维傅里叶变换。公式(5)指出,每一外推层的波场由两部分组成,一是在背景速度场中传播的波场,二是由二次震源引起的散射波场。波场在背景介质中的传播由相移公式(6)描述,二次震源引起的散射波场由公式(7)描述。当垂直波数趋于0时,方程(7)有一个奇点。为了避免出现这个问题,将1/kz展开为Taylor级数：

(8)

将(8)式代入(7)式,有：

Fx,y[iωΔS(x,y,z)U(ω,x,y,z)]

=Fx,y[iωΔS(x,y,z)U(ω,x,y,z)]+

(9)

(9)式可进一步分裂为：

U(ω,x,y,z)]

(10)

Fx,y[iωΔS(x,y,z)U(ω,x,y,z)]

(11)

在窄传播角的情况下,1/kz≈1成立,可以由(6)式和(10)式组成裂步傅里叶偏移方法。在宽传播角情况下,可以由(6)式、(10)式和(11)式组成广义屏偏移方法。由于傅里叶变换没有局部性,而速度摄动是横向变化的,具有很强的局部性,因此必须将(10)式变换回频率-空间域：

(12)

本文在仅考虑窄传播角的情况下,由(6)式和(12)式组成裂步傅里叶偏移方法,即在频率-波数域和频率-空间域中交替进行以下计算：①在频率-波数域中进行相移偏移,收敛绕射波;②在频率-空间域中校正由于横向速度变化引起的时差。

2基于GPU的三维起伏地表单程波叠前深度偏移实现

本文基于SSF偏移原理,在炮域进行三维单程波叠前深度偏移,沿着深度方向逐层延拓成像。每层成像包括以下5步：①二维傅里叶正变换,将频率-空间域的上行波场和下行波场转换到频率-波数域;②对频率-波数域上行波场和下行波场分别进行相移计算;③二维傅里叶反变换,将相移后的频率-波数域上行波场和下行波场变回到频率-空间域;④对频率-空间域上行波场和下行波场分别进行时移计算;⑤进行上行波场和下行波场相关成像,并对各频率成像值进行积分,获得偏移值。

三维起伏地表单程波偏移的GPU实现主要包括基于GPU的偏移计算和起伏地表偏移。为了提高算法的实用性,我们开发了相位校正和共成像点道集快速提取技术。

2.1GPU单程波偏移算法

在SSF单程波偏移每层5步的计算中,包括4次傅里叶变换和2次相移、2次时移、2次相关求和。分析可知,傅里叶变换的计算耗时最长,因此GPU偏移算法的重点是调用GPU版本的傅里叶变换。GPU运算平台CUDA提供了专门用于傅里叶变换的函数库cuFFT,包含了一系列的快速傅里叶变换函数,主要有cufftPlanMany,cufftExecC2C,cufftExecR2C,cufftExecC2R,cufftDestroy等。其中,cufftPlanMany函数是在傅里叶变换前创建一个计划(plan),cufftDestroy函数是在傅里叶变换后销毁这个计划;cufftExecC2C,cufftExecR2C,cufftExecC2R函数分别用于执行单精度复数域到复数域的傅里叶变换、单精度实数域到复数域的傅里叶变换和单精度复数域到实数域的傅里叶变换。在CUDA上进行傅里叶变换包括3步：①应用cufftPlanMany函数创建一个计划;②使用cufftExecC2C,cufftExecR2C或cufftExecC2R等函数执行计划,单程波偏移FFT是将单精度浮点数从复数域变换到复数域,因而调用的是cufftExecC2C函数;③调用cufftDestroy函数销毁上述计划以及为其分配的计算资源。cuFFT对信号长度比较敏感,当信号的长度为奇数时,运算速度较慢;当信号的长度为偶数时,运算速度较快;当信号长度为2的幂次时,运算速度最快。因此,执行cuFFT之前需要对二维空间网格进行镶边,使得x,y方向的空间网格数为2的幂次,或者2的幂次的倍数,达到快速实现傅里叶变换的目的。相移、时移、相关求和这3个运算具有相似的程序结构,都包括x方向、y方向和频率三重循环,可通过GPU多线程计算,达到并行加速的目的。

基于GPU的单程波叠前深度偏移单炮流程如图1,其中橙红色范围为GPU计算部分。

2.2起伏地表偏移

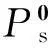
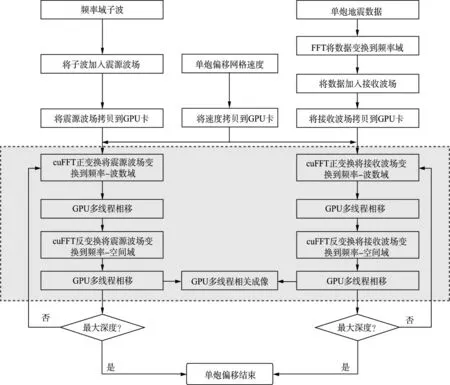
图1　单程波叠前深度偏移单炮流程

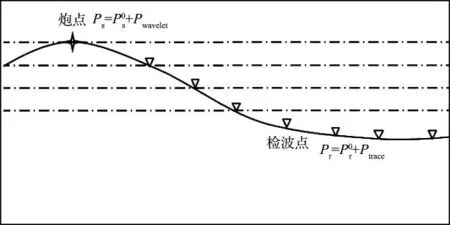
图2　起伏地表单程波偏移

2.3相位校正

假设炮点和检波点波场都是脉冲,炮点位于(x0,y0),检波点位于(x0+2hx,y0+2hy),hx和hy为x,y方向的偏移距,则炮点脉冲波场为：

(13)

检波点脉冲波场为：

r(t,x,y)=w(t)⊗δ(t-tδ)δ(x-x0-2hx)·

(y-y0-2hy)

(14)

其中,w(t)是脉冲子波,tδ为脉冲的走时。

按照单程波偏移原理,炮检点波场延拓到深度z并进行互相关成像的结果为：

(15)

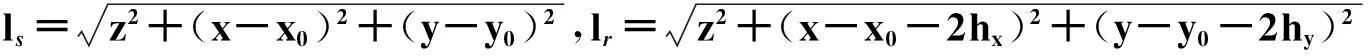
对于叠前偏移而言,一炮偏移的结果是所有偏移距检波点成像值的积分,叠加结果相对于原始子波相移了90°[17],因此,单程波偏移后有必要对成像结果进行相位校正[24]。本文采用希尔伯特变换实现90°相位校正。假设成像剖面中一道地震信号为s(t),希尔伯特变换后为：

(16)

图3a是某实际资料单程波偏移结果,图3b是相位校正后的结果,对比可见相位校正后波形更接近于零相位子波,与输入地震数据一致。

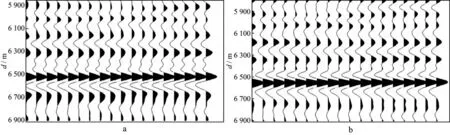
图3　某实际资料单程波偏移结果a 相位校正前; b相位校正后

2.4偏移距域共成像点道集提取

偏移距域共成像点道集提取是一个投影过程。对偏移结果中每一道数据,首先由成像点位置和炮点位置确定成像点和偏移距,然后将炮偏移数据体中该道数据投影叠加到共成像点道集数据体的相应道上。这种道集提取方式需要在偏移过程中将每一炮的偏移结果记录到磁盘。通常三维工区有数万炮采集数据,全部偏移结果大致有10～20TB,数据量非常大。另外,一般三维工区要生成的共成像点道集有100GB以上,超过计算机内存大小,如果把道集数据体存到磁盘上,则会出现频繁的磁盘IO操作,效率非常低。针对这两个问

题,本文在每个计算节点上将炮域偏移结果保存到节点的本地磁盘,偏移后基于MPI,采取数据索引的方式逐块进行共成像点道集的并行提取。具体实现步骤如下：

1) 按节点最大可使用内存对共成像点道集数据体进行分块,确定每块包含多少线数;

2) 每个节点逐道读取本地磁盘的单程波偏移数据道头信息,由炮点坐标和成像点坐标确定该道数据要投影的道集位置,包括块序号、线号、CDP号和一个道集内的道号,创建数据索引信息;

3) 逐块按照数据索引提取共成像点道集,主节点负责每块共成像点道集数据体的归约和写入,最终得到工区的偏移距域共成像点道集。

图4是某实际资料采用Kirchhoff叠前深度偏移方法和单程波叠前深度偏移方法得到的成像道集,偏移距范围为100～7000m。对比可见,单程波偏移方法在连续性、分辨率方面均好于Kirchhoff偏移方法,尤其是深度6500m以下的目的层段,Kirchhoff偏移结果存在明显的低频能量,而单程波偏移结果则具有较高的分辨率。

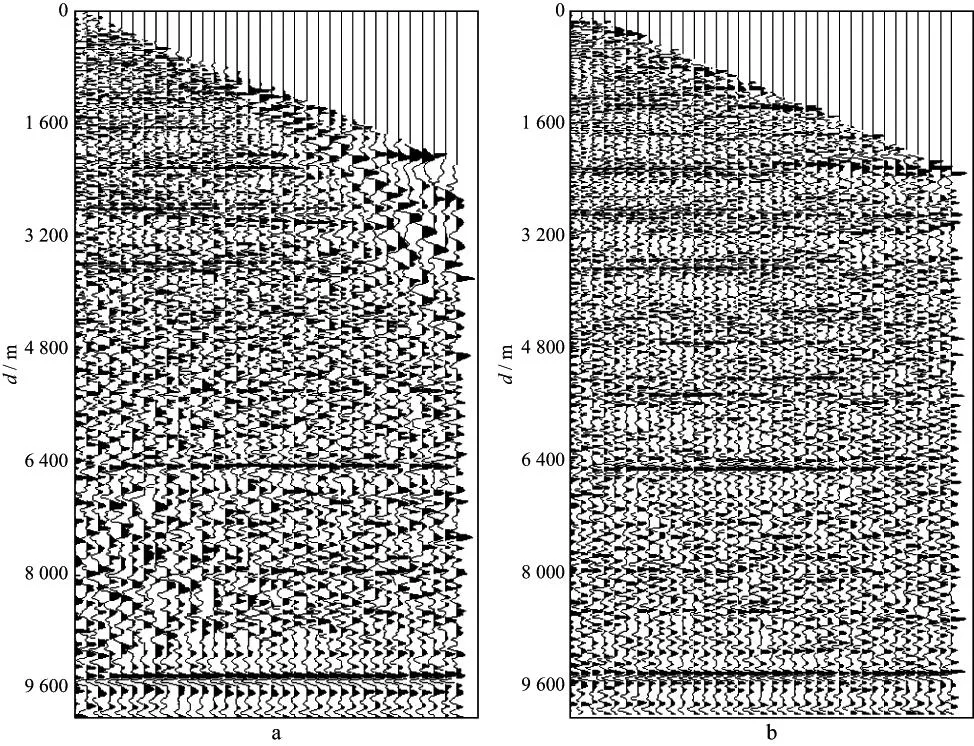
图4　某实际资料成像道集对比a Kirchhoff叠前深度偏移; b 单程波叠前深度偏移

3应用实例

3.1断块成像

中原油田某探区属典型高原沙化戈壁地貌,冲沟密布,海拔高差约300m。尽管地表起伏不是很大,但低降速带变化较为剧烈,横向岩性变化较大,影响静校正处理的精度。同时,地下构造断层十分发育,勘探目标层位破碎,且火成岩广泛分布,厚度变化剧烈,属于构造-岩性复合油气藏。获得较宽有效频带和断层清晰的成像剖面是落实该区断块圈闭、断层+岩性圈闭形态的必要条件。采用本文单程波叠前深度偏移方法对该探区42222炮资料进行了试处理,成像面积为570km2,计算网格大小为12.5m×25.0m,成像深度是11.5km,成

像频率为2～60Hz。采用84个GPU节点(每节点2块Tesla K10 GPU卡)共耗时25h。图5是单程波固定面叠前深度偏移和起伏地表叠前深度偏移剖面,可见单程波偏移方法能够较好地实现该探区断块成像,剖面整体分辨率高,波组特征清晰。对比图5中绿色圈内部分可见,起伏地表偏移对断层的刻画略好于固定面偏移。

3.2缝洞成像

我国西部某探区勘探目标为奥陶系碳酸盐岩古岩溶缝洞储层,具有埋藏深度大,发育规模小,非均质性强等特点。含油气层发育在风化壳的顶部,由于风化壳界面两侧较大的波阻抗差异,地震剖面上表现为强反射,掩盖了风化壳顶部储层发育的反射特征变化。采用本文单程波叠前深度偏移方法对该探区65445炮资料进行了处理,成像面积为1650km2,计算网格大小为25m×25m,成像深度是12km,成像频率为2～60Hz。采用84个GPU节点(每节点2块Tesla K10 GPU卡)共耗时65h。采用相同的计算资源和计算参数,利用GPU逆时偏移软件处理该资料总耗时为389h。图6是西部探区某测线单程波叠前深度偏移和逆时偏移剖面的浅层部分对比,可见两者基本一致,单程波叠前深度偏移剖面上浅层同相轴连续性略好。图7是目标层范围单程波叠前深度偏移和逆时偏移成像剖面,绿色圈内部分为“串珠”反射,对比可见单程波叠前深度偏移结果和逆时偏移结果基本一致。

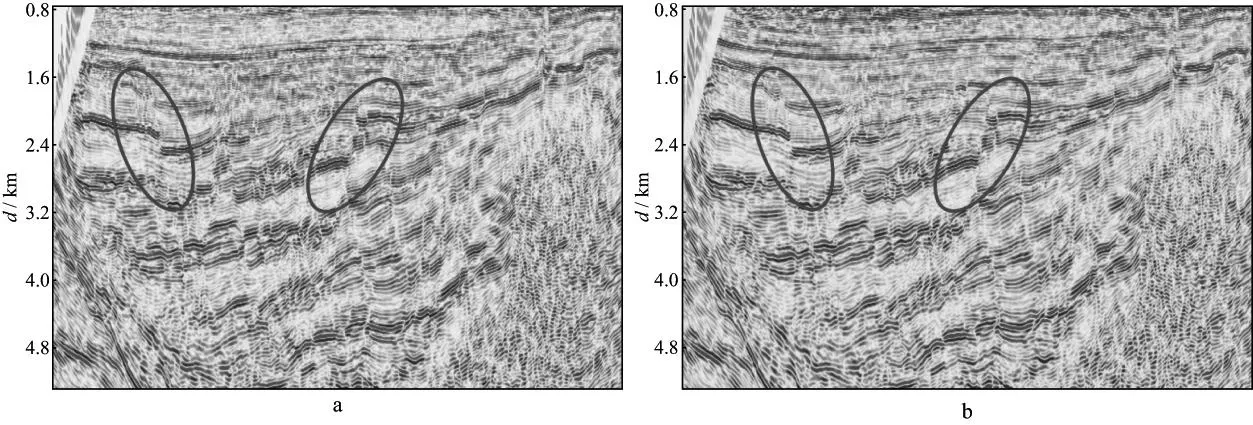
图5　中原油田某探区单程波叠前深度偏移剖面a 固定面偏移; b 起伏地表偏移

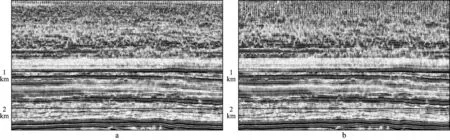
图6　西部探区某测线偏移剖面浅层部分a 单程波叠前深度偏移; b 逆时偏移

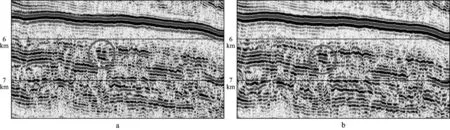
图7　西部探区某测线偏移剖面目标层部分a 单程波叠前深度偏移; b 逆时偏移

4结束语

本文在SSF单程波偏移原理基础上研究了GPU加速计算、起伏地表偏移、相位校正和偏移距共成像点道集提取等技术,取得以下成果：①利用GPU版本的傅里叶变换函数库提高了三维SSF偏移算法的计算效率。②采用逐步累加波场的思想提高了单程波偏移对复杂地表探区资料的适应性。③利用希尔伯特变换对偏移后数据进行相位校正,提高了成像结果与输入地震数据的相位一致性。④开发了基于分布式炮域成像结果的偏移距域道集并行提取技术,实现了单程波偏移道集的快速提取。实际资料应用结果表明,本文研究成果在复杂断块成像和缝洞成像方面具有较好的应用价值。

参考文献

[1]黄建平,孙陨松,李振春,等.一种基于分频编码的最小二乘裂步偏移方法[J].石油地球物理勘探,2014,49(4):702-707

HUANG J P,SUN Y S,LI Z C,et al.Least-squares split-step migration based on frequency-division encoding[J].Oil Geophysical Prospecting,2014,49(4):702-707

[2]黄建平,薛志广,步长城,等.基于裂步DSR的最小二乘偏移方法研究[J].吉林大学学报(地球科学版),2014,44(1):369-374

HUANG J P,XUE Z G,BU C C,et al.The study of least-squares migration method based on split-step DSR[J].Journal of Jilin University:Earth Science Edition,2014,44(1):369-374

[3]GAZDAG J.Wave-equation migration with the phase-shift method[J].Geophysics,1978,43(7):1342-1347

[4]STOH R H.Migration by Fourier transform[J].Geophysics,1978,43(1):23-48

[5]CLAERBOUT J F.Imaging the earth’s interior[M].Oxford：Blaekwell Scientific Publications,1985:4-30

[6]STOFA P L,FOKKEMA J T,LUNA F,et al.Split-step Fourier migration[J].Geophysics,1990,55(2):410-421

[7]RISTOW D,RUHL T.Fourier finite-difference migration[J].Geophysics,1994,59(12):1882-1893

[8]BERKHOUT A J.Wave field extrapolation techniques in seismic migration[J].Geophysics,1981,46(11):1638-1656

[9]DE HOOP M V,LO ROUSSEAU J H,WU R S.Generalization of the phase-screen approximation for the scattering of acoustic waves[J].Wave Motion,2000,31(1):43-48

[10]丁伟,李振春,刘玉莲.基于Born/Rytov近似的联合叠前深度偏移方法[J].石油物探,2003,42(1):29-34

DING W,LI Z C,LIU Y L.The prestack depth migration method based on Born/Rytov approximations[J].Geophysical Prospecting for Petroleum,2003,42(1):29-34

[11]方伍宝,孙建国,赵改善,等.波动方程叠前深度偏移成像软件系统的研制及应用[J].石油物探,2005,44(5):486-460

FANG W B,SUN J G,ZHAO G S,et al.The imaging software system of wave equation prestack migration[J].Geophysical Prospecting for Petroleum,2005,44(5):486-460

[12]张宇,徐升,张关泉,等.真振幅全倾角单程波方程偏移方法[J].石油物探,2007,46(6):582-587

ZHANG Y,XU S,ZHANG G Q,et al.True amplitude turning-wave one-way wave equation migration[J].Geophysical Prospecting for Petroleum,2007,46(6):582-587

[13]方伍宝,张兵.单程波外推高陡倾角反射成像技术的应用研究[J].石油物探,2009,48(5):488-452

FANG W B,ZHANG B.Application of reflection imaging technology with one-way wave extrapolation in high and steep structure[J].Geophysical Prospecting for Petroleum,2009,48(5):488-452

[14]王立歆,马方正.基于改进的时移成像条件的保幅叠前深度偏移研究[J].石油物探,2010,49(3):222-226

WANG L X,MA F Z.Amplitude-preserved prestack depth migration based on modified time-lapse imaging condition[J].Geophysical Prospecting for Petroleum,2010,49(3):222-226

[15]张兵,赵改善,黄俊,等.地震叠前深度偏移在CUDA平台上的实现[J].勘探地球物理进展,2008,31(6):427-432

ZHANG B,ZHAO G S,HUANG J,et al.Seismic prestack depth migration on the CUDA platform[J].Progress in Exploaration Geophysics,2008,31(6):427-432

[16]刘奇琳,黄跃,唐建明,等.波动方程叠前深度偏移的GPU技术[J].物探化探计算技术,2010,32(4):386-391

LIU Q L,HUANG Y,TANG J M,et al.Wave equation pre-stack depth migration with GPU[J].Computing Techniques for Geophysical and Geochemical Exploration,2010,32(4):386-391

[17]LIU H W,LIU H,SHI X D.GPU based PSPS one-way high resolution migration[J] Expanded Abstracts of 82ndAnnual Internat SEG Mtg,2012:1-5

[18]RESHEF M.Depth migration from irregutar surfaces with the depth extrapolation methods[J].Geophysics,1991,56(1):119-122

[19]BEASLEY L W.The zero velocity layer:migration from irregular surfaces[J].Geophysics,1992,57(11):1435-1443

[20]何英,王华忠,马在田.复杂地形条件下波动方程叠前深度成像[J].勘探地球物理进展,2002,25(3):13-19

HE Y,WANG H Z,MA Z T.Pre-stack wave equation depth migration for irregular topography[J].Progress in Exploaration Geophysics,2002,25(3):13-19

[21]王成祥,赵波,张关泉.基于起伏地表的混合法叠前深度偏移[J].石油地球物理勘探,2002,37(1):219-223

WANG C X,ZHAO B,ZHANG G Q.Rugged surface oriented hybrid pre-stack depth migration[J].Oil Geophysical Prospecting,2002,37(3):219-223

[22]田文辉,李振春,张辉.直接下延法波动方程叠前深度偏移[J].石油物探,2006,45(5):447-451

TIAN W H,LI Z C,ZHANG H.Direct continuation method based on wave equation for prestack depth migration[J].Geophysical Prospecting for Petroleum,2006,45(5):447-451

[23]卢宝坤,时维成,王立业.基于单程波波动方程的起伏地表叠前深度偏移技术[J].煤田地质与勘探,2012,40(6):71-74

LU B K,SHI W C,WANG L Y.One-way wave equation pre-stack depth migration from irregular surface[J].Coal Geology & Exploration,2012,40(6):71-74

[24]刘法启,单国健,MORTON S,等.单程波方程偏移算法的相位问题研究[J].石油物探,2007,46(6):598-603

LIU F Q,SHAN G J,MORTON S,et al.Study of phases in one way wave equation migration methods[J].Geophysical Prospecting for Petroleum,2007,46(6):598-603

(编辑：戴春秋)

3D one-way wave equation prestack depth migration from topography based on the acceleration of GPU

DUAN Xinbiao1,2,WANG Huazhong1,BAI Yingzhe2,WANG Lixin2,ZHANG Huiyu2,HE Ying2

(1.WavePhenomenaandInversionImagingGroup(WPI),TongjiUniversity,Shanghai200092,China;2.SinopecGeophysicalResearchInstitute,Nanjing211103,China)

Abstract:Compared with two-way wave equation reverse time migration,One-way wave equation migration possesses several attractive features such as higher computational efficiency,better bandwidth imaging result (particularly rich in high-frequency signals) and more flexible to obtain common imaging gathers (CIGs).It is adaptable for many domestic land seismic exploration areas without high-dip structures.Aiming at huge 3-D land seismic data of complex surface exploration areas,we present 3D one-way wave equation prestack depth migration from topography based on the acceleration of GPU,using split-step Fourier (SSF) operator.In addition,we introduce a phase correction technique for one-way wave equation migration result and an offset domain CIGs extraction technique based on distributed shot images.Two typical land data examples of complex fault imaging and fracture-cavity reservoirs imaging illustrate that our method can describe these reservoirs relatively precisely with high computational efficiency,so it has a high value of practical application to the exploration areas without strong lateral velocity variation and high-dip structures.

Keywords:one-way wave equation migration,common-offset gathers,split-step Fourier (SSF) operator,prestack depth migration

文章编号：1000-1441(2016)02-0223-08

DOI:10.3969/j.issn.1000-1441.2016.02.008

中图分类号：P631

文献标识码：A

基金项目：国家科技重大专项(2011ZX05014)资助。

作者简介：段心标(1982—),男,博士在读,现从事地震偏移成像方法研究工作。

收稿日期：2015-04-22;改回日期：2015-10-28。

This research is financially supported by the National Science and Technology Major Project of China (Grant No.2011ZX05014).