导电围岩对井中三维瞬变电磁响应的影响规律研究

杨怀杰,潘和平,孟庆鑫,郭　博

(1.中国地质大学(武汉)地球物理与空间信息学院,湖北武汉430074;2.河北地质大学勘查技术与工程学院,河北石家庄050031)



导电围岩对井中三维瞬变电磁响应的影响规律研究

杨怀杰1,潘和平1,孟庆鑫2,郭博1

(1.中国地质大学(武汉)地球物理与空间信息学院,湖北武汉430074;2.河北地质大学勘查技术与工程学院,河北石家庄050031)

摘要:简要设计地质模型,应用时域有限差分法对模型空间进行非均匀网格剖分,选取磁偶源和不同阶廖氏边界条件,实现了井中均匀全空间和含低阻体的三维瞬变电磁场数值模拟,获得了不同电阻率目标体在导电围岩内电磁场的传播特征以及不同导电围岩对瞬变电磁响应的影响规律。数值模拟结果表明:围岩电阻率越大,电磁总场的极大值出现的时刻越早,随时间衰减越快,且衰减到后期,总场不受围岩电阻率的影响,衰减值几乎相同。

关键词：瞬变电磁法;有限差分;导电围岩;异常场;廖氏吸收边界

井中瞬变电磁法是将发射线圈和接收线圈置于同一口井中激发并接收电磁场信号、探测地下目标体的地球物理勘探方法。发射线圈和接收线圈的组合有多种方式,如同点装置、偶极装置、中心回线装置等[1]。受地面地震勘探的启发,我们采用发射线圈和接收线圈阵列组合装置,一个线圈发射信号,多个线圈接收信号,这种装置能提高电磁场信号的采集率。

国外关于瞬变电磁法的研究已经取得了许多成果,如WOODS[2]和DYCK[3]研究了均匀全空间内三维瞬变电磁法的数值模拟方法，但是早期的研究结果存在计算速度慢、计算精度低等问题。1984年,MCNEILL等[4]以激励源为初始条件,模拟了导电围岩内三维板状体的瞬变电磁场。1988年,RICHARD等[5]利用积分方程法分析了地-井方式导电半空间内三维水平断裂带的瞬变电磁响应特征，该方法只需将异常体离散化,未知量少,计算精度高,但难以适用于复杂地质体。

国内井中瞬变电磁法的研究工作起步较晚。2007年,岳建华等[6]提出了矿井全空间瞬变电磁场的时域有限差分法,选择Mur吸收边界条件,将激励源作为初始条件,模拟了均匀介质中巷道底部、岩层内部和层状介质中三维低阻异常体的电磁场传播规律;2010年,杨海燕等[7]推导了全区视电阻率公式,并在矿井瞬变电磁法资料处理与解释中取得了较好的效果;2011年,宋汐瑾等[8]采用Gaver-Stehfest逆拉氏变换方法,正演计算了瞬变信号激励下接收线圈上的电磁场响应;2013年,孟庆鑫等[9]应用时域有限差分法,采用显式差分方程,选取磁偶极子源作为初始条件和不同阶Mur吸收边界条件,对包含低阻异常体的均质全空间电磁场进行了三维数值模拟。

本文应用时域有限差分法和廖氏吸收边界条件,对磁偶源产生的瞬变电磁场进行三维数值模拟,研究了井中均匀全空间背景场和含低阻薄板全空间异常场的传播规律、不同电阻率目标体在导电围岩内电磁场的传播规律,以及不同导电围岩对瞬变电磁响应的影响规律。

1基本原理

1.1差分方程

忽略位移电流,无源且均匀各向同性线性介质中电磁场的麦克斯韦方程为:

(1)

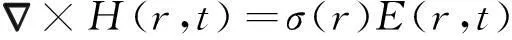
(2)

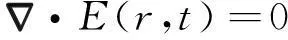
(3)

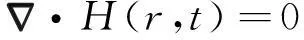
(4)由公式(1)至(4)可以推导出电磁场的无源扩散方程:

(5)

(6)式中:E(r,t)为电场强度,H(r,t)为磁场强度;μ和σ(r)分别为磁导率和电导率。

在直角坐标系下,采用非均匀网格将有限计算区域剖分成若干个长方体单元,使方程(5)和方程(6)的无限大区域求解转化为各小长方体单元节点的求解,相邻网格边长的步长按指数递增。在剖分好的网格内利用Dufort-Frankel法离散电场和磁场强度的无源扩散方程,将连续的电磁场值转化为网格节点上的离散值,得到总场扩散方程的七点差分格式[10-11]:

(7)

其中,

(8)式中:An(i,j,k)表示n时刻点(i,j,k)处的瞬变电场强度或者磁场强度;Δxi,Δyj和Δzk为直角坐标系下3个方向的空间步长;Δt为计算区域内的时间步长。对计算区域进行非均匀网格剖分,在直角坐标系下以发射源所在的位置为中心,3个方向的空间步长按指数关系增长(图1),初始步长为0.5m,底数为1.2。

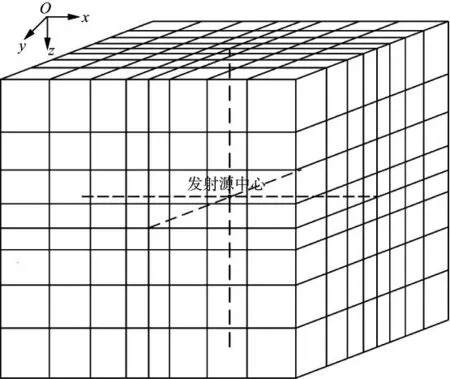
图1　非均匀网格剖分数值计算区域

1.2场源与初始条件

三维时域有限差分算法中,激励源选择均匀全空间中磁偶源的解析式作为初始条件,与目标体在深度上要存在一定距离。均匀全空间中磁偶源产生的磁场垂直分量解析式为[10]:

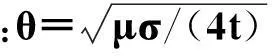
1.3边界条件

数值计算区域边界电磁场的吸收采用廖氏吸收边界条件,采用这种方法可以进行高阶校正,对边界角点处理效果较好,计算精度较高。N阶廖氏边界条件在6个截断边界面上的方程为[11]:

(10)

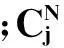
(11)

六面体计算区域的12个棱和8个角边界采用2阶廖氏边界条件,6个面边界采用3阶廖氏边界条件。

2均匀全空间瞬变电磁场数值模拟

2.1地质模型及井下瞬变电磁装置

在直角坐标系下对磁偶源产生的瞬变电磁场进行三维数值模拟,设计地质模型如图2a所示,W1,W2和W3为3口钻井。数值计算区域为100m×100m×100m,坐标原点O为钻井与计算区域上表面的交点。地质模型中目标体的大小为20m×20m×2m,W1井穿过目标体,距目标体右端的距离为5m,W2和W3井没有穿过目标体,距目标体右端的距离分别为5m和10m。

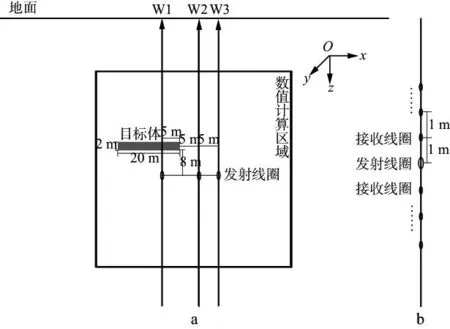
图2　井中三维地质模型(a)与发射、接收排列方式(b)

发射线圈和接收线圈采用阵列组合排列方式(图2b)在井轴上发射和接收信号,中心位置的发射线圈和接收线圈采用重叠回线装置,发射线圈上下各排列25个接收线圈,相距均为1m。发射线圈半径为0.1m,匝数为40,电流强度为10A,断开电流后,51个接收线圈接收各个时刻的瞬变响应信号。

2.2均匀全空间电磁场扩散规律

采用图2a所示W2井地质模型,分析数值模拟结果的准确性,模型空间内不含异常体。图3是井中全空间坐标点(5,0,50)在0.2～3.2μs时刻总电场强度的解析解与数值模拟结果对比图,可见两者测试数据点吻合,曲线走势相似。根据对比分析,文中选择小于3.2μs时刻的数值模拟结果。

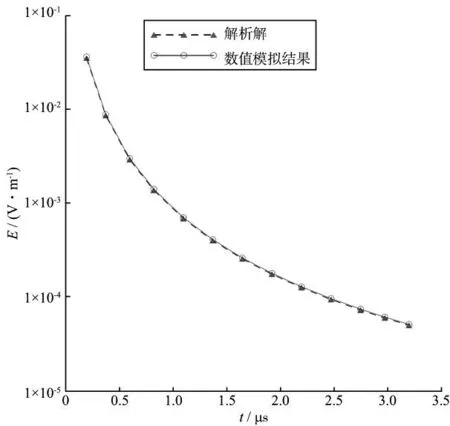
图3　井中全空间点解析解与数值模拟结果对比

为了节约计算时间,数值计算区域设置为40m×40m×40m,目标体设置为10m×10m×2m,接收线圈位于目标体之下,垂直深度距离为8m,围岩电阻率为100Ω·m,目标体电阻率为10Ω·m。

全空间不含异常体时,接收线圈接收的信号为总场(记为H或者E),也可以看作是背景场。全空间中含有异常体时,发射线圈断开电流的瞬间异常场为零,此时接收线圈接收的总场也是背景场[12]。随着时间的推移,感应电流传播到异常体时,忽略电流彼此之间的互感影响,接收线圈接收的总场可以看作是背景场(记为H′或者E′)和异常场(记为ΔH或者ΔE)响应的叠加[1,5,13]。图4a和图4b分别为0.2μs和0.9μs时刻均匀全空间不含异常体电场的等值线图。可以看出,此时的总场是背景场,以发射源为中心,逐渐向外扩散。图5a 和图5b分别为0.2μs和0.9μs时刻含异常体均匀全空间异常电场等值线图。可以看出,排除背景电场的影响,异常电场的传播以低阻体为中心逐渐向外扩散。

由图4a和图5a可见,在较早的时刻,背景场和异常场以相反的方向传播,此时的总场小于背景场。由图4b和图5b可见,随着时间推移到一定时刻,异常场最大值主要集中在异常体附近,异常体附近的背景场逐渐衰减,此时的总场通常大于背景场。然而异常场衰减速度比背景场衰减速度快,所以衰减到后期总场几乎等于背景场。

2.3异常体对瞬变电磁响应的影响

采用图2a所示地质模型,模拟了W1,W2和W3三口井情况下不同电阻率异常体对瞬变电磁响应的影响规律。围岩电阻率保持不变,为100Ω·m,目标体电阻率分别取1,5,10,15,20,30,40,50,60,70,80,90,100Ω·m。图6是0.45μs时刻3口钻井(W1,W2和W3)的目标体异常磁场垂直分量随薄板电阻率变化的曲线。

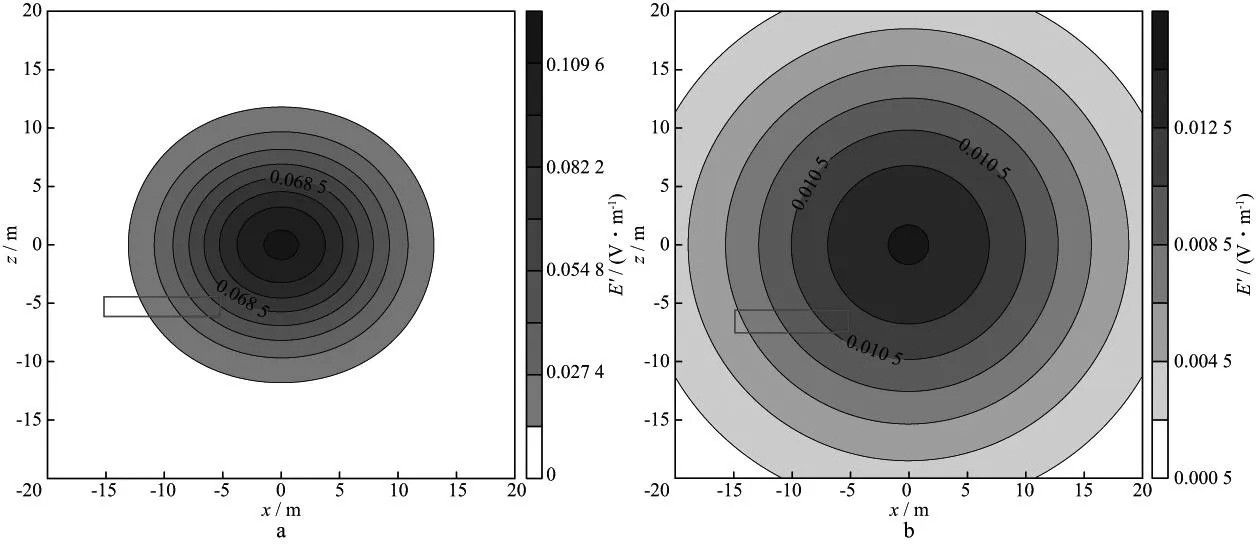
图4　xoz切面背景电场等值线(围岩电阻率100Ω·m,目标体电阻率10Ω·m)a t=0.2μs; b t=0.9μs

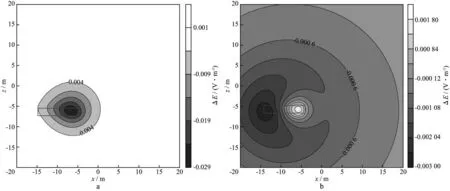
图5　xoz切面异常电场等值线(围岩电阻率100Ω·m,目标体电阻率10Ω·m)a t=0.2μs; b t=0.9μs

由图6可见,当钻孔穿过目标体时(W1井),目标体异常场大小随电阻率的增加而增加,当电阻率增大到40Ω·m时,异常场增速变缓,响应逐渐趋于稳定。当钻孔与目标体在横向上存在一定距离后(W2井和W3井),目标体电阻率分别在达到30Ω·m和20Ω·m时,异常场增速变缓,响应逐渐趋于稳定。地质模型3口钻井情况下,随着目标体电阻率的增加,异常场由不同的低值增加到相同的值,其中W1井的起始值最低,说明发射线圈与目标体越近,目标体的异常场出现的时间越早,衰减越快。

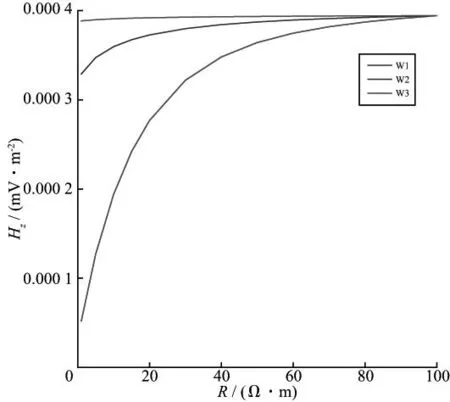
图6　井中异常磁场垂直分量随目标体电阻率变化的曲线

2.4导电围岩对瞬变电磁响应的影响

采用图2a所示地质模型,模拟了W1,W2和W3三口井情况下不同导电围岩对瞬变电磁响应的影响规律。目标体电阻率保持不变,为1Ω·m,围岩电阻率分别取10,20,30,40,50,60,70,80,90,100,200,300,400,500Ω·m。图7展示了0.45μs时刻3口钻井(W1,W2和W3)的目标体异常磁场垂直分量随围岩电阻率变化的曲线。由图7可见,目标体的异常场随着围岩电阻率的增大先增大后减小,极大值出现在围岩电阻率偏小的时候,出现极大值后异常场则随围岩电阻率的增大而减小,瞬变电磁响应逐渐趋于稳定。

在图2a所示W1井情况下,随着围岩电阻率的增大,目标体异常磁场在围岩电阻率较小时出现极大值。在图2a所示W2和W3井情况下,目标体异常磁场出现极大值时的围岩电阻率大于W1井出现极大值时的围岩电阻率,说明围岩电阻率越大,目标体与围岩的相互作用越强,产生的异常场越大。W1井钻孔穿过目标体,异常场的极大值最小;W2井和W3井钻孔与目标体在横向上存在一定距离,异常场的极大值变大,距离越大,异常场的极大值越大。由此可见,发射线圈与目标体的横向距离越远,异常场极大值出现的时刻越晚,衰减越慢。

图8是W1井中不同电阻率的导电围岩引起的磁场垂直分量变化曲线,导电围岩的电阻率分别为40,60,80,100,120,140,160,180Ω·m,目标体的电阻率为1Ω·m。由图8可见,随着导电围岩电阻率的减小,总场的极大值逐渐增大,且出现极大值的时间逐渐向后推迟;围岩电阻率越大,总场衰减越快,衰减到后期,水平薄板的异常场不受导电围岩的影响,衰减值几乎相同。

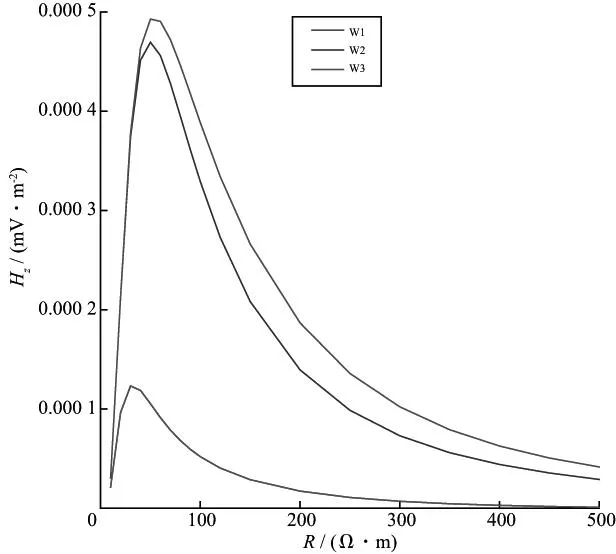
图7　井中异常磁场垂直分量随围岩电阻率变化曲线

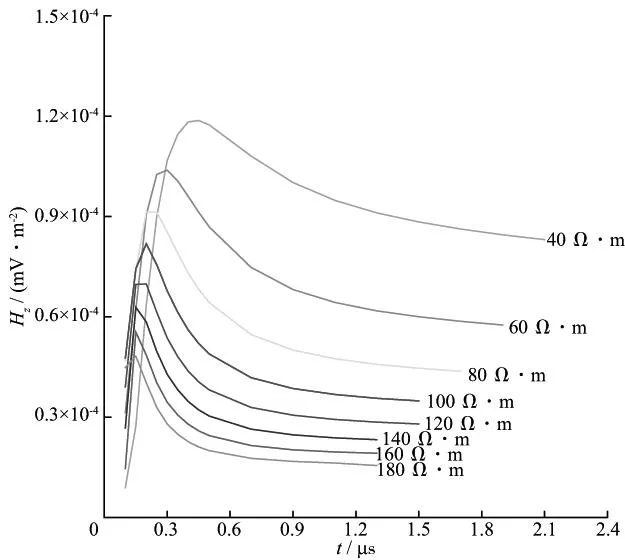
图8　井中受不同电阻率导电围岩影响的薄板磁场垂直分量变化曲线

3结论与认识

本文应用时域有限差分法和廖氏吸收边界条件对磁偶源产生的瞬变电磁场进行了三维数值模拟研究,获得了井中均匀全空间背景场和含低阻薄板全空间异常场的传播规律、不同电阻率异常体在导电围岩内电磁场的传播规律,以及不同导电围岩对瞬变电磁响应的影响规律。通过分析各种情况下电磁场的传播特征,取得以下认识:

1) 均匀全空间总电磁场可以看作是背景场,以发射源为中心,逐渐向外扩散;异常电场的传播以低阻体为中心逐渐向外扩散。

2) 在较早时刻,背景场和异常场以相反的方向传播,总场小于背景场;随着时间的推移,异常场最大值主要集中在异常体附近,异常体附近的背景场逐渐衰减,此时总场大于背景场。

3) 相同时刻、相同电阻率围岩,目标体异常场随着电阻率的增大而增大,当电阻率增大到一定值时,异常场增速变缓,响应趋于稳定状态。当钻孔穿过目标体时,异常场由最低值逐渐增加,随着钻孔与目标体距离的增加,异常场从不同的低值逐渐增加到相同的值。

4) 相同时刻、相同电阻率目标体,异常场随着围岩电阻率的增大先增大后减小,响应逐渐趋于稳定状态。极大值在围岩电阻率较小时出现,且钻孔穿过目标体时异常场最小,钻孔与目标体距离越大,异常场的极大值越大。

5) 随着导电围岩电阻率的减小,异常体总场的极大值逐渐增大,且出现极大值的时刻逐渐向后推迟;围岩电阻率越大,总场衰减越快,衰减到后期,水平薄板的总场不受导电围岩的影响,衰减值几乎相同。

需要指出的是,井中瞬变电磁响应特征复杂,本文为了采集足够的数据,设置接收线圈之间间隔为1m,忽略了线圈之间的相互感应作用。此外,模拟轴对称介质中的瞬变电磁响应时,采用柱坐标系比较合适。

参考文献

[1]牛之琏.时间域电磁法原理[M].湖南长沙:中南大学出版社,2007:249-267

NIU Z L.The principle of time domain electromagnetic method[M].Changsha:Central South University Press,2007:249-267

[2]WOODS D Y.A model study of the Crone borehole pulse electromagnetic (PEM) system[D].Kingston,Ontario:Queen’s University,1975

[3]DYCK A Y.A method for quantitative interpretation of wideband drill-hole EM surveys in mineral exploration[D].Toronto:University of Toronto,1981

[4]MCNEILL L D,EDWARDS R N,LEVY G M.Approximate calculations of the transient electromagnetic response from buried conductors in a conductive half-space[J].Geophysics,1984,49(7):918-924

[5]RICHARD C W,STANLEY H W.The borehole transient electromagnetic response of a three-dimensional fracture zone in a conductive half-space[J].Geophysics,1988,53 (11):1469-1478

[6]岳建华,杨海燕.矿井瞬变电磁法三维时域有限差分数值模拟[J].地球物理学进展,2007,22(6):1904-1909

YUE J H,YANG H Y.3D finite difference time domain numerical simulation for in-time TEM[J].Progress in Geophysics,2007,22(6):1904-1909

[7]杨海燕,邓居智,张华,等.矿井瞬变电磁法全空间视电阻率解释方法研究[J].地球物理学报,2010,53(3):651-656

YANG H Y,DENG J Z,ZHANG H,et a1.Research on full-space apparent resistivity interpretation technique in mine transient electromagnetic method[J].Chinese Journal of Geophysics,2010,53(3):651-656

[8]宋汐瑾,党瑞荣,郭宝龙,等.井中磁源瞬变电磁响应特征研究[J].地球物理学报,2011,54(4):1122-1129

SONG X J,DANG R R,GUO B L,et al.Research on transient electromagnetic response of magnetic source in borehole[J].Chinese Journal of Geophysics,2011,54(4):1122-1129

[9]孟庆鑫,潘和平.井中磁源瞬变电磁三维时域有限差分数值模拟[J].中南大学学报,2013,44(2):649-655

MENG Q X,PAN H P.3D FDTD numerical simulation for transient for transient electromagnetic of magnetic source in borehole[J].Journal of Central South University,2013,44(2):649-655

[10]纳比吉安.勘查地球物理电磁法[M].北京:地质出版社,1992:155-351

NABIGHIAN M N.Electromagnetic methods in applied geophysics[M].Beijing:Geological Publishing House,1992:155-351

[11]杨海燕.矿用多匝小回线源瞬变电磁法数值模拟与分布规律研究[D].江苏徐州:中国矿业大学,2009

YANG H Y.Study on numerical simulation and distribution regularity of transient electromagnetic field with mine-used multi small loop[D].Xuzhou:China University of Mining and Technology,2009

[12]KAUFMANN A A.Frequency and transient responses of electromagnetic fields created by currents in conductors[J].Geophysics,1978,43(5):1002-1010

[13]李建慧,朱自强,鲁光银,等.回线源瞬变法的三维正演研究[J].地球物理学进展,2013,28(2):754-765

LI J H,ZHU Z Q,LU G Y,et al.Study on three-dimensional forward of transient electromagnetic method excited by loop source[J].Progress in Geophysics,2013,28(2):754-765

(编辑：戴春秋)

Influence laws of conductive host on borehole 3D transient electromagnetic responses

YANG Huaijie1,PAN Heping1,MENG Qingxin2,GUO Bo1

(1.InstituteofGeophysics&Geomatics,ChinaUniversityofGeosciences,Wuhan430074,China; 2.SchoolofProspectingTechnologyandEngineering,HebeiUniversityofGeosciences,Shijiazhuang050031,China)

Abstract:The geological model is designed simply and is non-uniform meshed by using the finite difference in time domain,the magnetic dipole source and different-order Liao absorbing boundary are selected,to simulate the 3-D transient electromagnetic field in borehole uniform whole space with a low resistivity body.Meanwhile,the propagation characteristics of the electromagnetic field,which contain different resistivity targets in the surrounding rock,are simulated; and the rules of influence of different conductive surrounding rock on the transient electromagnetic response are analyzed.Numerical simulation results show that when the host is more conductive,appearing time of the total field is earlier and the attenuation is faster along with time.The total field of target body appears to be independent from the conductivity of the host at the later period,and the decay value is almost the same.

Keywords:transient electromagnetic method,finite difference,conductive host,anomaly field,Liao absorbing boundary

文章编号：1000-1441(2016)02-0288-06

DOI:10.3969/j.issn.1000-1441.2016.02.015

中图分类号：P631

文献标识码：A

基金项目：国家自然科学基金项目(4107408)资助。

作者简介：杨怀杰(1987—),男,博士在读,主要从事地球物理测井与井中电磁法理论研究。

收稿日期：2015-04-30;改回日期：2015-07-13。

This research is financially supported by the National Natural Science Foundation of China (Grant No.4107408).