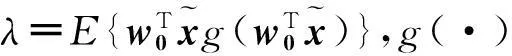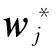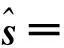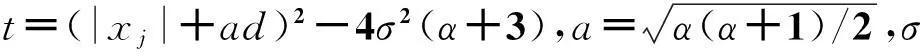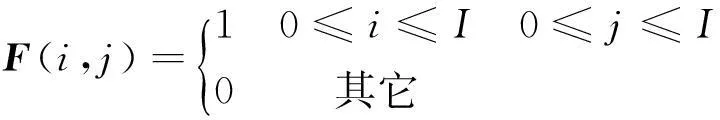基于独立分量分析基的地震随机噪声压制

孙成禹,邵　婕,蓝　阳,唐　杰

(中国石油大学(华东)地球科学与技术学院,山东青岛266580)



基于独立分量分析基的地震随机噪声压制

孙成禹,邵婕,蓝阳,唐杰

(中国石油大学(华东)地球科学与技术学院,山东青岛266580)

摘要:传统的独立分量分析(Independent Component Analysis,ICA)去噪方法假设地震记录的相邻道含有相同的随机噪声,仅适用于同相轴较平的地震记录,去噪效果并不显著。为了改善ICA方法对高斯随机噪声的压制效果,首先通过构造度量数据非高斯性的目标函数求取地震数据的ICA基,将数据转换至ICA域;然后通过贝叶斯方法构造出满足非高斯分布的阈值函数,进行阈值法去噪处理。为了满足独立分量分析的假设条件,将地震数据进行分块处理,并假设每个数据块与整体的数据含有相似的数据结构。理论模型及实际资料试算结果表明,该方法可以有效地压制剖面中的高斯随机噪声,对含复杂界面的数据也十分有效,具有较好的应用价值。

关键词：独立分量分析;ICA基;高斯随机噪声压制;贝叶斯阈值函数

压制随机噪声的方法有很多,如均值滤波、中值滤波、基于小波变换或曲波变换的阈值去噪方法以及基于独立分量分析(ICA)的去噪方法等。但随着地震勘探程度的不断提高及勘探目标的日益复杂,对去噪技术的要求也越来越高。独立分量分析技术是实现盲源分离的有效手段,它考虑了数据的高阶统计特性,因而能更加全面地表达数据的本质特征[1]。刘喜武等[2]假设地震记录中的有效信号和随机噪声具有统计意义的相互独立性质且服从非高斯分布,利用某道记录的多次观测结果或邻近多道记录,通过独立分量分析算法直接从地震记录中分离出有效信号及非高斯随机噪声[3]。此后很多学者对独立分量分析的算法进行了改进,如李大卫等[4]提出了模拟退火独立分量分析方法,并将其应用于共反射点道集中有效信号和干扰信号的分离,提高了分离信号的质量。张银雪等[5]为了改善常规固定步长独立分量分析算法在叠前资料中的去噪效果,提出了基于混沌粒子群优化(Particle Swarm Optimization,PSO)的改进ICA算法。这些改进的独立分量分析方法能有效地压制地震数据中的高斯随机噪声,但通常假设输入的相邻道记录中包含相同的随机噪声,这在实际生产中很难得到满足。为了改善ICA技术压制加性高斯随机噪声的效果,吕文彪等[6]先应用两步特征值分解法去除部分加性噪声的影响,再利用ICA算法成功地分离出原信号。郭科等[7]利用改进的ICA预处理算法去除加性高斯噪声,采用特征矩阵联合对角化(Joint Approximate Diagonalization of Eigenmatrices)盲分离算法分离出有效信号和非高斯分布的随机噪声。王维强等[8]利用经验模态分解(Empirical Mode Decomposition,EMD)能将信号自适应分解为不同尺度振动模态的优点及独立分量分析能提取独立源信号的优势,提出了一种EMD和ICA相结合的去噪算法,很好地实现了地震有效信号和随机噪声的分离。

上述方法虽然改善了ICA算法的去噪效果,但通常只适用于同相轴较平的叠后记录,且运算效率比较低。本文通过构造度量数据非高斯性的目标函数及寻优算法确定输入数据的ICA基,将地震记录转换至ICA域进行去噪处理,以进一步改善ICA方法对高斯随机噪声的压制效果。

1独立分量分析(ICA)

1.1基函数

在信号处理领域,为了有效地分析数据的本征结构,人们通常将其表述为一系列基向量的线性组合,提出了各种不同的基函数,如傅里叶变换中的正弦、余弦基,以及小波基、曲波基等。这些基函数通常有确定的表达式,可以将数据变换到不同的域中进行分析。由于不同数据所隐含的数据结构并不相同,确定的基函数无法突出信号的某些特征,因此,我们定义包含基函数所需性质的目标函数,对输入数据进行训练,通过优化算法确定适用于任意输入数据的基函数。

设数据x(k,l)的大小为M×N,k=1,2,…,M,l=1,2,…,N,可表示为K个基向量pj(k,l)的线性组合:

(1)

式中:yj为对应基向量pj(k,l)的表示系数,yT=[y1,…,yK],P=[p1(k,l),…,pK(k,l)]。通过(1)式,观测信号被投影到一组基向量张成的空间内。由此看来,确定一组能够捕捉输入数据大部分结构的基函数是有效描述信号特征问题的关键,可以通过独立分量分析的方法来获得基向量pj(k,l)及其对应的表示系数yj。

1.2ICA基

独立分量分析本质上也是一种优化算法,它可以确定统计意义上相互独立的基向量[9]。中心极限定理表明,如果观测信号可以表示为一组基向量的组合,且具有最小的高斯性,信号便是独立的。因此,统计独立和非高斯性是等价的,构造ICA目标函数的关键便是度量分离结果的非高斯性[6]。当(1)式中表示系数yj的非高斯性达到最大时,所确定的基向量相互独立。

度量非高斯性的方法有很多,如高阶累积量、熵及互信息等[10]。本文选用负熵的方法,其定义如下:

(2)

其中,yG是均值为0、与y具有相同方差的高斯随机变量,H(y)是随机变量的熵,其定义式为:

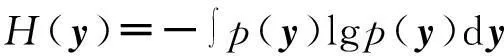
(3)

式中,p(y)为y的概率密度函数。由(2)式可知,当y服从高斯分布时,J(y)=0;非高斯变量的熵H(y)为非负值,非高斯性越强,其值越大。

(4)

其中,E{·}为随机变量的均值;G(·)是非二次函数,其表达形式有很多[12],本文选用的公式为:

(5)

式中:a,b为常数;c为取值较小、控制数值稳定性的常数(c≈0.1)。

为了求取J(y)的最大值,HYVRINEN[11]提出了固定点算法,又称为FastICA方法。该算法首先对原始数据x进行预处理,主要是进行零均值化及白化,其中白化可通过主成分分析(Principal Component Analysis,PCA)方法实现。用主成分分析法对零均值化处理后的数据的协方差矩阵进行特征值分解，可实现数据的降维处理。这一过程用线性变换V来表示,则有:

(6)

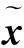
(7)

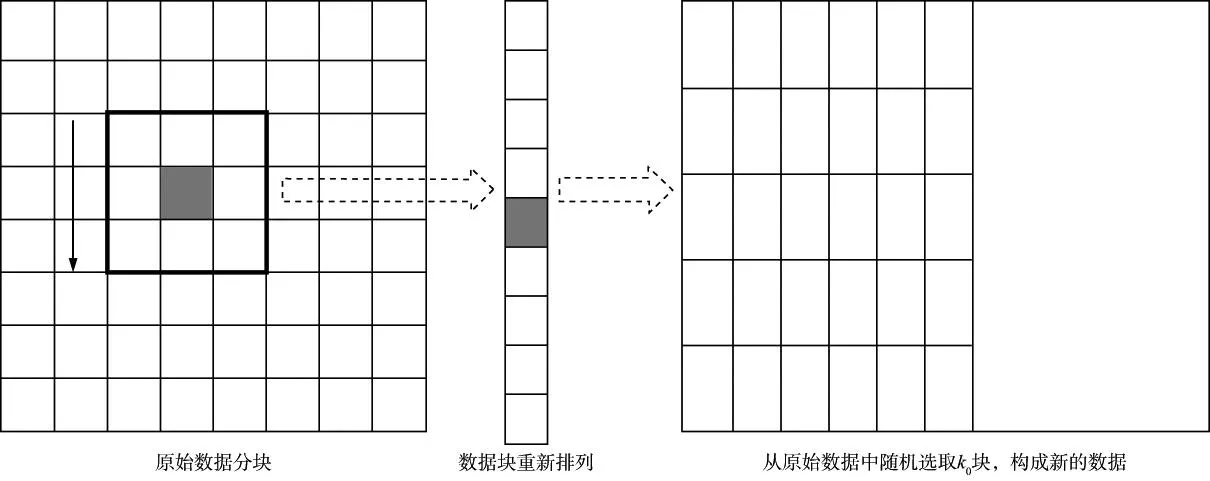
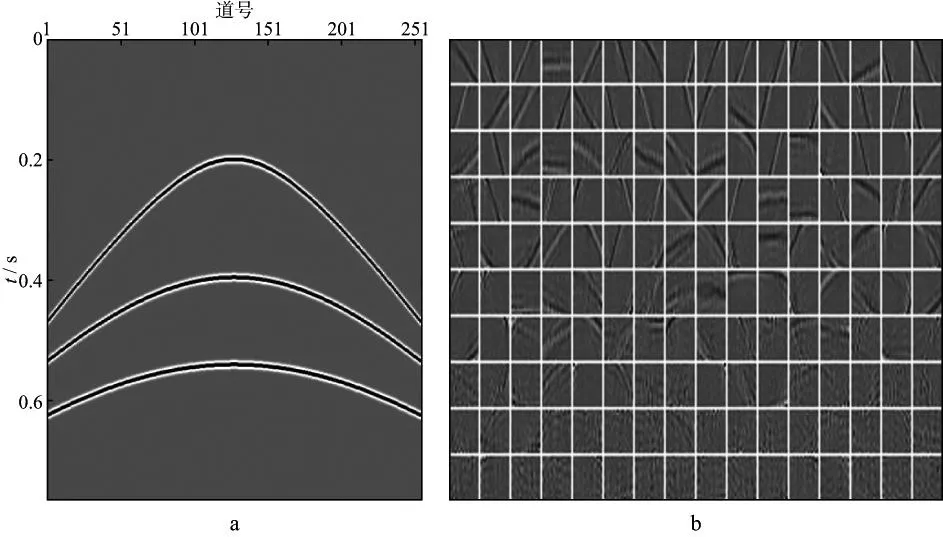
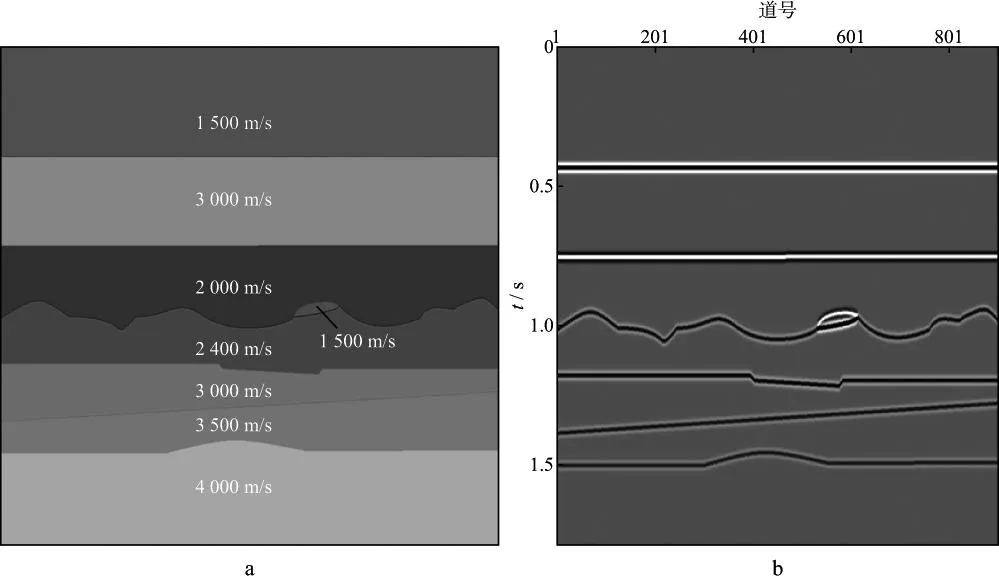
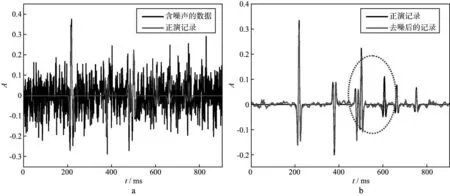
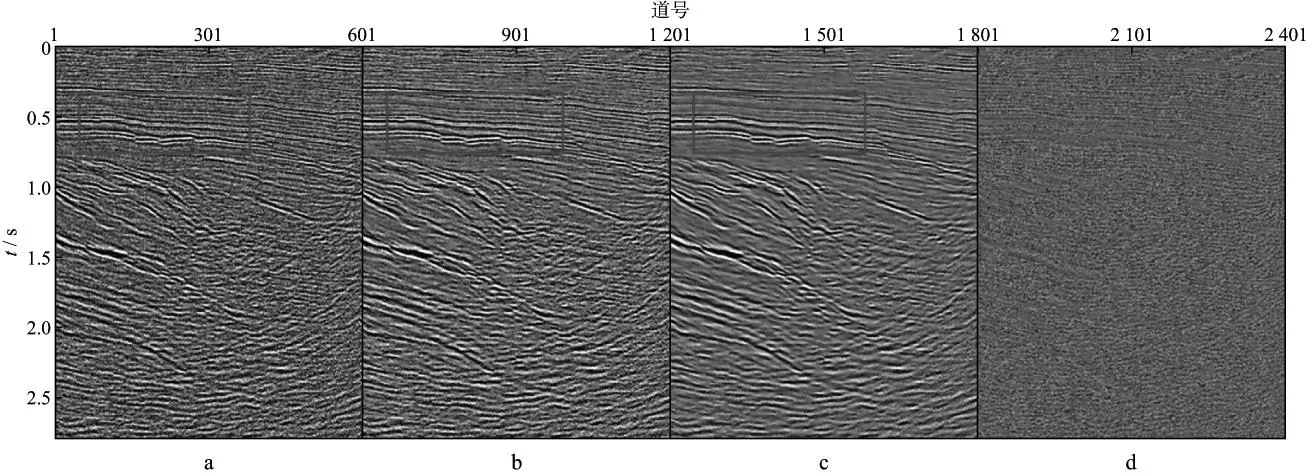
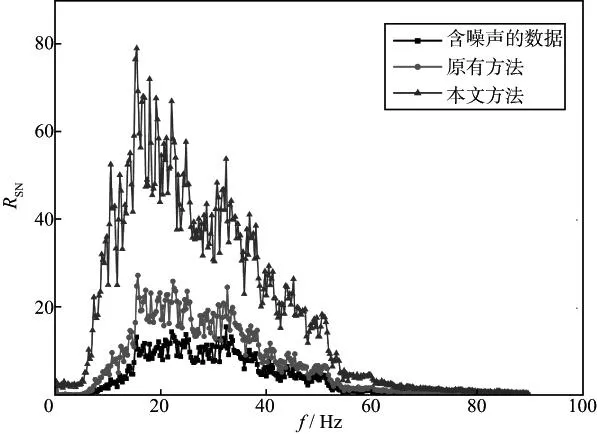
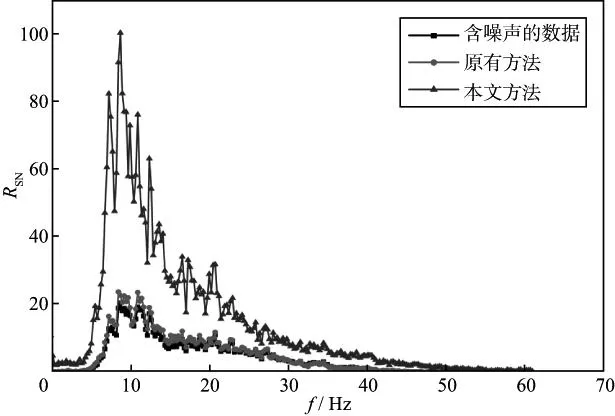
通常将V称作为PCA基(由主成分分析算法求得)[13]。从公式(7)中选取L

(8)

通过牛顿迭代法求解方程(8),最终得到FastICA算法的迭代公式为:

(9)

(10)

将求得的ICA基及其逆矩阵作用于相应的数据,便可以实现空间域与ICA域间的相互映射。

图1　地震记录分块及重排列

由ICA的约束条件可知,观测信号的个数应不少于源信号的个数,但对于地震数据而言,通常只有一个观测结果。传统的ICA方法通常选取某道记录邻近的几道记录作为输入,并假设其含有相同的随机噪声。但这种假设并不符合实际情况,去噪效果也不显著。本文借鉴图像处理中的分块处理方式[15-16],将地震记录进行分块处理,得到相同大小的子剖面。假设这些子剖面包含的数据结构与原始剖面相似,将每一子剖面作为观测信号进行ICA处理,便可以得到反映地震记录整体性质的基函数。在实际处理中,为了简化运算过程,通常将分块得到的二维子剖面按一定的顺序(图1中实线箭头所示)转化为一维数组。此外,为了节省运算时间,并不对所有的一维子块进行处理,而是随机地选取k0块(k0≥1000)构成一个新的输入矩阵,如图1所示。将此输入矩阵作为上述ICA算法的输入,求出分离矩阵W及混合矩阵W-1,进而求出ICA基。图2为模拟的正演记录以及通过上述方法得到的ICA基。在计算过程中,地震数据被划分为16×16(样点数)大小的子块。为了提高运算效率,从划分的数据块中随机地选取1500块作为ICA算法的输入。为了形象地显示基函数,将求得的基函数(长度n=256)变换为16×16的矩阵。

图2　正演记录(a)和ICA基(b)

2基于ICA基的阈值法去噪

野外观测的含噪声地震记录如下:z=s+n

在实际应用中,有效信号合理的概率密度估计

p(s)及其参数选取问题是去噪技术的关键,但对于各接收道而言,数据之间存在着复杂的统计依赖性,难以确定统一的p(s)函数。为此,借助独立分量分析的特有性质,使原始数据变换后各分量间的统计依赖性更小(即相互独立),且使分离后各信号的非高斯性达到最大。即:Pz=Ps+Pn

(13)其中,P为上述ICA算法确定的变换算子,它将数据由空间域映射到ICA域。对于任意的P,Pn仍服从高斯分布,因此,可以选取具有非高斯分布特点的概率密度函数作为先验信息,并通过(12)式中的贝叶斯方法实现对随机噪声的压制。

服从非高斯分布的概率密度函数有多种不同的形式,本文选用的形式如

(14)其中,d为向量s的标准差,α为控制p(sj)形式的参数,其表达式如下:

(15)其中,k=d2p(0)2。当α→∞时,公式(14)为拉普拉斯分布。

将公式(14)代入公式(12)中,并求其最大值,推导后得:

(16)

图3　基于ICA基的去噪处理算法流程

除了上述阈值函数外,我们也可以考虑其它形式的概率分布,从而得到不同的阈值算法[19]。图3为基于ICA基的去噪处理算法流程,其主要包括如下步骤。1) 将大小为M×N的地震数据进行分块,即选取大小为I×I的窗函数对原始记录从左到右或从上到下做重叠分块,并按照其存储位置将其转化成I×I×1的向量(按列顺序)。所选用的窗函数如下:

(17)

2) 从分块处理得到的数据块中随机选取k0块(k0≥1000)作为FastICA算法的输入,求出ICA域的分离矩阵W及混合矩阵W-1,进而求出将数据由空间域映射至ICA域的基向量P-1。

3) 利用求得的ICA基将地震数据映射到ICA域,并采用蒙特卡罗方法[20]求取噪声的方差估算值σ,然后通过阈值方法压制随机噪声。

4) 通过P将处理后的数据由ICA域映射到空间域,并按照先前的分块顺序对数据进行重新组合。

5) 由于ICA算法固有的不确定性,处理后数据的振幅值相对于原始数据整体相差一个倍数,因此需要对处理后的数据进行重构,但这并不改变数据间振幅的相对关系。

3模型测试及实际资料处理

3.1理论模型测试

为了验证上述算法的去噪效果,建立如图4a所示的速度模型,并通过正演模拟得到图4b所示的地震剖面。该模型既包含了常见的水平及倾斜界面,又包含了复杂的弯曲界面、断层及透镜体。在原始剖面中加入信噪比为1.08的高斯随机噪声(图5a),图5b为采用传统的独立分量分析方法去除随机噪声后的剖面；图5c为采用本文方法去噪后的剖面,去噪前数据被划分为10×10大小的子块,并随机地选取1000块数据作为ICA算法的输入。

对比图5b和图5c可知,本文方法的去噪效果要明显好于传统方法,剖面中的大部分随机噪声都得到了有效压制,且有效信号的损失较少,即使是那些弯曲程度较大的复杂同相轴,有效信号的损失也比较少，相比之下,传统方法在复杂同相轴处的有效信号损失较为严重。图5d为含噪声的地震剖面与本文方法去噪后的地震剖面差值,可以看出差值剖面中残留的有效信号较少。

图4　理论速度模型(a)和正演地震剖面(b)

图5　理论模型的去噪效果a 含噪声的原始剖面; b 传统方法去噪后的剖面; c 本文方法去噪后的剖面; d 本文方法去除的随机噪声

对图5c中虚线处(CDP2400)的地震道进行波形分析,结果如图6所示。图6a为上述地震道正演模拟的波形及加噪后的波形对比图,可以看出,深层的弱信号完全淹没在噪声中,无法得到有效识别。图6b为该地震道正演模拟的波形及去噪后的波形对比图,可以看出深层的弱信号得到了有效恢复,虚线圈内所示透镜体处的信号几乎没有损失,但断层处的信号略有损失，这主要是在去噪过程中直接将小于阈值的幅值赋零造成的。

图6　图5c中虚线处(CDP2400)地震道去噪效果分析a 有效信号及含噪声数据的波形分析; b 有效信号及去噪后数据的波形分析

3.2实际资料处理

选取A地区实际地震资料,利用本文独立分量分析方法对其进行去噪处理。数据被划分为10×10大小的子块,并随机地选取1500块数据作为ICA算法的输入。去噪结果如图7所示,其中,图7a为含噪声的原始地震剖面,图7b为采用传统独立分量分析方法去噪后的剖面,图7c为采用本文方法去噪后的剖面。对比图7a至图7c可以看出,两种方法都能使原始剖面中的随机噪声得到有效压制,但本文方法的去噪效果要好于传统方法,整个剖面上的同相轴变得更加连续、光滑,如图中红线框内所示。图7d为本文方法去除的随机噪声,即图7a和图7c两图的差值剖面,可以看出,本文方法去噪后损失的有效信号比较少。

为了精确地显示去噪处理对原始数据信噪比的改善情况,计算了两种方法去噪前后地震剖面的信噪比谱[21],结果如图8所示。可以看出,两种方法去噪后各个频带内的信噪比都得到了改善,但本文方法去噪后的信噪比要大于传统方法去噪后的信噪比。计算信噪比谱的公式如下:

(18)

图7　A地区实际资料去噪效果a 含噪声的地震剖面; b 原有方法去噪后的剖面; c 本文方法去噪后的剖面; d 本文方法去除的随机噪声

式中:Ps(f)为有效信号的功率谱,即第i道记录与第i+1道记录的互相关;Pz(f)为n道记录的平均功率谱。

(19)

(20)

其中，Zi(f)为第i(i=1,2,…,n)道原始记录的振幅谱。

图9a为B地区含噪声的地震剖面,该剖面同相轴较为倾斜,且含有断点现象,随机噪声使剖面中的断点不清晰,无法有效地追踪整个断层的延伸情况,如图9a中红色箭头所示。图9b为采用本文方法去噪后的剖面,同相轴变得光滑、连续,随机噪声得到了有效的压制,断点清晰可见,更加有利于小断层的追踪。图9c为采用传统方法去噪后的剖面,虽然随机噪声得到了一定程度的压制,但与图9b 相比,去噪效果较差。图9d为本文方法去除的随机噪声。

图8　A地区实际资料去噪前后的信噪比谱

为了进一步分析本文方法的去噪效果,截取图9a 中虚线框内的断层区域进行局部显示,如图10所示。由图10可见，去噪前虚线框内蓝色箭头所示的断点位置无法进行有效识别(图10a)，采用本文方法去噪后不仅可以准确地确定虚线框内断点的位置,实线框内的断点也更加清晰(图10b),而原有方法去噪后部分断点处仍较为模糊,如图10c中虚线框内箭头所示。求取图9中两种方法去噪前后地震剖面的信噪比谱,如图11所示。由图11可以看出,对于较为复杂的地震剖面,原有方法去噪后的结果信噪比改善不大,而本文方法去噪后各个频带内的信噪比都得到大大提升。

图9　B地区实际资料去噪效果a 含噪声的地震剖面; b 本文方法去噪后的剖面; c 原有方法去噪后的剖面; d 本文方法去除的随机噪声

图10　B地区实际资料去噪前后的局部显示a 含噪声的地震剖面; b 本文方法去噪后的剖面; c 原有方法去噪后的剖面

图11　B地区实际资料去噪前后的信噪比谱

4结束语

本文通过构造度量数据非高斯性的目标函数,利用寻优算法确定适应数据自身特点的ICA基,将数据转换至ICA域进行去噪处理，获得以下结论与认识:

1) 通过独立分量分析使分离后有效信号的非高斯性最大,随机噪声仍满足高斯分布,根据贝叶斯理论推导出满足该分布情况下的阈值函数,结合阈值法去噪技术,可以压制剖面中的高斯随机噪声。

2) 与传统的基于独立分量分析的去噪算法不同在于,本文方法对数据进行分块处理,假设每一个数据块所含的基函数与整体数据的基函数相同,仅选取部分数据块进行训练,运算效率得以提高。

3) 通过构造的基函数将数据转换至ICA域进行去噪处理,可以有效地避免传统独立分量分析方法仅适用于较平同相轴的问题,使其适用于复杂剖面。

需要注意的是,本文选用的阈值函数简单、实用性强,但其直接将小于阈值的幅值赋零,会损害地震数据中的部分弱信号。因此,下一步研究目标是推导出更加符合地震数据特征的概率分布函数,得到更加复杂的阈值函数,用于含弱信号地震数据的随机噪声压制。

参考文献

[1]COMMON P.Independent component analysis,a new concept?[J].Signal Processing,1994,36(3):287-314

[2]刘喜武,刘洪,李幼铭.快速独立分量变换与去噪初探[J].中国科学院研究生院学报,2003,20(4):488-492

LIU X W,LIU H,LI Y M.Independent component transform and its testing application on seismic noise elimation[J].Journal of the Graduate School of the Chinese Academy of Sciences,2003,20(4):488-492

[3]彭才,朱仕军,孙建库,等.基于独立成分分析的地震数据去噪[J].勘探地球物理进展,2007,30(1):30-33

PENG C,ZHU S J,SUN J K,et al.Seismic denoising based on independent component analysis method[J].Progress in Exploration Geophysics,2007,30(1):30-33

[4]李大卫,尹成,谢兵.模拟退火独立分量分析方法及其应用[J].石油物探,2007,46(1):24-27

LI D W,YIN C,XIE B.Simulated annealing independent component analysis method and its application[J].Geophysical Prospecting for Petroleum,2007,46(1):24-27

[5]张银雪,田学民.基于改进PSO-ICA的地震信号去噪方法[J].石油地球物理勘探,2012,47(1):56-62

ZHANG Y X,TIAN X M.Seismic denoising based on improved PSO-ICA method[J].Oil Geophysical Prospecting,2012,47(1):56-62

[6]吕文彪,尹成,张白林,等.利用独立分量分析法去除地震噪声[J].石油地球物理勘探,2007,42(2):132-136

LV W B,YIN C,ZHANG B L,et al.Seismic denoising using independent component analysis method[J].Oil Geophysical Prospecting,2007,42(2):132-136

[7]郭科,陈聆,陈辉,等.基于JADE算法的地震资料随机噪音盲分离方法研究[J].地学前缘,2011,18(3):302-309

GUO K,CHEN L,CHEN H,et al.The method of seismic random noise blind separation based on JADE[J].Earth Science Frontiers,2011,18(3):302-309

[8]王维强,杨国权.基于EMD与ICA的地震信号去噪技术研究[J].石油物探,2012,51(1):19-29

WANG W Q,YANG G Q.The study of seismic denoising based on EMD and ICA[J].Geophysical Prospecting for Petroleum,2012,51(1):19-29

[10]刘杰.基于独立分量分析的地震盲反褶积方法及应用研究[D].山东东营:中国石油大学(华东),2008

LIU J.Study on independent component analysis- based seismic blind deconvolution method and its application[D].Dongying:China University of Petroleum (East China),2008

[13]芮挺,沈春林,TIAN Q,等.ICA与PCA特征提取能力的比较分析[J].模式识别与人工智能,2005,18(1):124-128

RUI T,SHEN C L,TIAN Q,et al.Comparison and analysis on ICA & PCA's ability in feature extraction[J].Pattern Recognition and Artificial Intelligence,2005,18(1):124-128

[14]HANSON M A.Invexity and the Kuhn-Tucker theorem[J].Journal of Mathematical Analysis and Application,1999,236(2):594-604

[15]刘琚,孙健德,徐宏吉.盲信号处理理论与应用[M].北京:科学出版社,2013:203-208

LIU J,SUN J D,XU H J.Theory and application of blind signal processing[M].Beijing:Science Press,2013:203-208

[16]NIKOLAOS M,STANTHAKI T.Optimal contrast correction for ICA-based fusion of multimodal images[J].IEEE Sensors Journal,2008,6(1):1-21

[17]SANCHIS C,HANSSEN A.Sparse code shrinkage for signal enhancement of seismic data[J].Geophysics,2011,76(6):V151-V167

[18]HOYER P.Independent compent analysis in image denoising[D].Espoo:Helsinki University of Technology,1999

[19]SENDUR,SELESNICK I W.Bivariate shrinkage functions for wavelet-based denoising exploiting interscale dependency[J].IEEE Transactions on Signal Processing,2002,50(11):2744-2756

[20]张恒磊,刘天佑.Curvelet 域蒙特卡罗估计的随机噪声衰减[J].西南石油大学学报(自然科学版),2011,33(4):64-68

ZHANG H L,LIU T Y.Seismic random noise attenuation via Monte Carlo estimator in curvelet domain[J].Journal of Southwest Petroleum University(Science & Technology Edition),2011,33(4):64-68

[21]张军华,藏胜涛,周振晓,等.地震资料信噪比定量计算及方法比较[J].石油地球物理勘探,2009,44(4):481-486

ZHANG J H,ZANG S T,ZHOU Z X,et al.Quantitative computation and comparison of S/N ratio in seismic data[J].Oil Geophysical Prospecting,2009,44(4):481-486

(编辑：戴春秋)

Seismic random noise suppression based on independent component analysis basis functions

SUN Chengyu,SHAO Jie,LAN Yang,TANG Jie

(SchoolofGeosciences,ChinaUniversityofPetroleum,Qingdao266580,China)

Abstract:Traditional seismic denoising methods based on independent component analysis (ICA) assume that adjacent traces in seismic record contain the same random noise.The denoising effect based on this assumption is not significant,and it is only suitable for seismic records with flat event.Therefore,we convert the seismic data to ICA domain by constructing an ICA basis according to the objective function measuring the non-Gaussianity and set a threshold to reduce the random noise.This threshold function is obtained by Bayesian method.In order to satisfy the assumption of independent component analysis,we carried out the partition processing on the seismic data and supposed that each data block has the similar structures with the whole data.The processing results of theoretical and real data show that this method can suppress the random noise effectively and it is suitable for seismic data with complex interface.So the denoising method based on independent component analysis has the obvious advantage and good application value for Gaussian random noise suppression.

Keywords:independent component analysis,independent component analysis (ICA) basis,Gaussian random noise suppression,Bayesian threshold function

文章编号：1000-1441(2016)02-0196-09

DOI:10.3969/j.issn.1000-1441.2016.02.005

中图分类号：P631

文献标识码：A

基金项目：国家自然科学基金(41374123)和国家科技重大专项(2011ZX05006-002)项目共同资助。

作者简介：孙成禹(1968—),男,教授,主要从事地震勘探理论和方法研究。

收稿日期：2015-06-03;改回日期：2015-08-10。

This research is financially supported by the National Science Foundation of China (Grant No.41374123) and the National Science and Technology Major Project of China (Grant No.2011ZX05006-002).