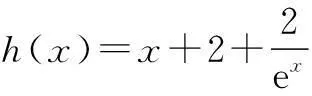深化知识理解 完善认知结构——一道试题的错解分析及其教学启示



深化知识理解完善认知结构
——一道试题的错解分析及其教学启示

刘永良

(广东省广州市玉岩中学,510530)

一、题目与错解

题目已知函数f(x)=(x2-ax+a)ex-x2,a∈R.若函数f(x)在x=0处取得极小值,求a的取值范围.

这是高三数学复习导数的应用时,学生作业中的一道题目,由于经验型思维错误及思维不严谨,学生中出现了以下两种错解.

错解1因为f′(x)=(x2-ax+2x)ex-2x,而f(x)在x=0处取得极小值,于是f′(0)=0,所以a∈R.

错解2由于函数f(x)在x=0处取得极小值,所以当x∈(-∞,0)时,f′(x)<0;当x∈(0,+∞)时,f′(x)>0.

因为f′(x)=(x2-ax+2x)ex-2x=x[(x-a+2)ex-2]，所以

(x-a+2)ex-2>0,

其中x∈(-∞,0)∪(0,+∞),

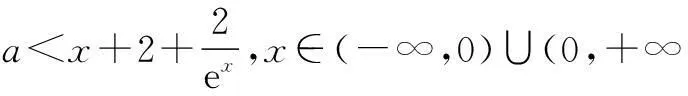
a

令h′(x)=0,得x=ln 2.

所以a的取值范围(-∞,3+ln 2).

二、剖析与正解

这两种错解对帮助学生理解函数极值存在的条件是很好的材料,我们将以上解法展示给学生,请学生进行判断.很快有学生提出质疑,认为两种解法均是错误的.他们是用特殊值法验证的:

若a=2,则f(x)=(x2-2x+2)ex-x2,

f′(x)=x2ex-2x=x(xex-2).

当x∈(-∞,0)时,f′(x)>0,当x∈(0,ln 2)时,f′(x)<0,从而当x=0时,函数f(x)取得极大值,因此x=0不是函数f(x)的极小值点.

因此前面两种解法均是错误的.于是笔者请学生进一步思考.错误出在哪一步呢?

函数f(x)在x=0处取得极小值,除了f′(0)=0外,是否一定要满足条件.当x∈(-∞,0)时,f′(x)<0;当x∈(0,+∞)时,f′(x)>0吗?

其实，函数f(x)在x=0处取得极小值,除了f′(0)=0外,不一定要x∈(-∞,0)时,f′(x)<0;x∈(0,+∞)时,f′(x)>0.而应该是函数f(x)在x=0的左右两侧的区间内,左边是减函数,右边是增函数就可以了.

学生们似有所悟!一会儿有学生给出了如下正确解法.

正解f′(x)=(x2-ax+2x)ex-2x=x[(x-a+2)ex-2],显然f′(0)=0,因此要使函数f(x)在x=0处取得极小值,需使f′(x)在x=0的左侧为负,右侧为正.

令h(x)=(x-a+2)ex-2,则只需h(x)在x=0的左、右两侧均为正.

h′(x)=(x-a+3)ex.

由h′(x)=0,得x=a-3，所以a≠3.

这时h(x)在(-∞,a-3)上是减函数,在(a-3,+∞)上是增函数,从而h(x)在x=a-3处取得最小值,且h(a-3)=-ea-3-2<0,

因此,要函数f(x)在x=0处取得极小值,只要h(0)=-a>0,即a<0.

所以a的取值范围是(-∞,0).

三、教学反思

1. 解题中的经验型思维错误值得反思

由于求解这类题目“已知函数f(x)=ex-ln(x+m),设x=0是f(x)的极值点,求m”时，学生常常采用的就是利用f′(0)=0,从而求出m=1,而教师也未明确地指出其问题,因此形成了学生的解题经验化,他们很快将新信息同化到原有的信息中,没有作精确分化,于是形成了错解1.这种由于受已有的数学知识和以往的解题经验影响而造成的思维障碍就是经验型思维错误,在教学中尤其值得反思.学生的这种解题错误往往是基于经验而产生的不正确的迁移,其根源还是在平时的学习中,对函数极值存在的充分与必要条件理解不准确.

2. 解题中思维不严谨导致的错误值得反思

对于错解2的形成,则是由于平时教学时把知识分解成了一个一个的小模块,从而导致学生局部地看问题,在思维的严谨性上有缺陷,这也是教学中值得思考的一个问题.错解2中有两处值得注意的问题.一是函数f(x)取得极小值的充分条件学生没有弄清楚.二是函数只有一个导数为0的值时,它是不是函数的最值,这些都是学生容易出错的地方.教学时要对知识结构精心组织,赋予知识点更多的信息,使它与其他知识发生一些外显的或内隐的联系,让学生在知识和经验之间建立起丰富的联系,形成良好的知识结构,从而使学生在解决问题的过程中形成全面严谨的思维.

3. 解题教学要在如何完善学生的认知结构上展开反思

学生解题中折射出的解题错误尤其值得深思,函数与导数渗透的主要数学思想方法是数形结合思想,这需要教师通过各种问题对学生进行经验的积累.除了定性研究,也必须开展定量研究,在定性与定量上适时切换.在解题中引导学生自觉地对“数”与“形”进行观察与化归,往往可以突破数学解题中的思维受阻状况.而学生得出的正确解法就得益于学生对函数与导数解题中的数形结合思想理解较为深刻,对函数极值存在的充分与必要条件理解得较好.数学学习是一个建立、扩展、精致认知结构的过程.“精致”或者是对原有认知结构的重组,或者是对原有认知结构缺陷的修补.高三数学复习要在完善学生的认知结构上开展教学,使学生已学的知识得到完整的理解,只有当知识结构得以概括化和系统化而形成高度整合时,知识技能才能转化为能力,这是发展学生数学能力和提高学生数学素质的必然途径.(本文系广州市教育科学“十二五”规划课题“基于知识心理发生的数学教学研究与实践”(课题编号2013B385)阶段研究成果之一.)