矩阵反可交换的研究
2016-04-22刘佳琦哈尔滨商业大学基础科学学院哈尔滨150028
袁 笛,刘佳琦(哈尔滨商业大学 基础科学学院, 哈尔滨 150028)
矩阵反可交换的研究
袁笛,刘佳琦(哈尔滨商业大学 基础科学学院, 哈尔滨 150028)
摘要:给出反可交换矩阵的一些性质,并给出一些矩阵反可交换的充分必要条件.
关键词:矩阵;反可交换;可逆矩阵
矩阵理论不单单是一种数学理论,且在医学、工程等领域发挥着重要作用.矩阵的运算不同于一般数的运算.数的运算满足的运算公式,矩阵运算并非成立.在矩阵运算中,如果AB=-BA,称A,B为反可交换矩阵.目前的研究状况下,对这类反可交换矩阵研究的相对较少[1-3],所以本文基于反可交换的定义[4],给出一些反可交换矩阵的一些性质、定理.以丰富矩阵反可交换理论部分的相关结果.本文的矩阵均指n阶实方阵.
定义1[5]:如果n阶矩阵A,B满足AB=-BA,则称矩阵A与B反可交换.
定理1设阶矩阵A与B反可交换,则:

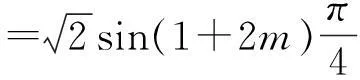
证明:使用数学归纳法证
首先当m=1时,有:
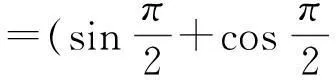

等式成立;
假设当m=k时等式成立,即:


下证当m=k+1时等式也成立.
当m=k+1时有:
(AB)k+1=(AB)k(AB)

即当m=k+1时等式仍然成立.
综上所述,可知定理得证.
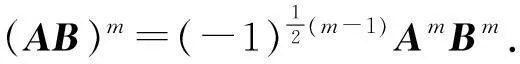
证明 由于矩阵A与B反可交换,所以有AB=-BA成立
(AB)m=(AB)(AB)…(AB)(m个AB)
=(-1)m-1A2B(AB)…(AB)B(m-2个AB)
=(-1)m-1+m-2A3B(AB)…(AB)B2(m-3个AB)
……
=(-1)(m-1)+(m-2)+…+AmBm
定理得证.
推论1[1]设阶矩阵A与B反可交换,
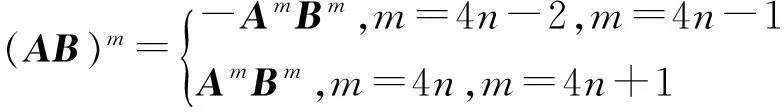
n=1,2,…
证明 当m=4n-2,m=4n-1时,
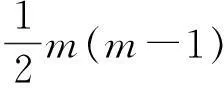
当m=4n,m=4n+1时,

所以有:
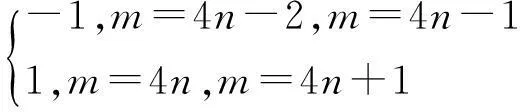
n=1,2,……
从而有:

n=1,2,…
故推论得证.
定理3设n阶矩阵A与B反可交换,若A与B均为幂零矩阵,则AB,A+B均为幂零矩阵.[6]
证明 已知n阶矩阵A与B反可交换,则AB=-BA显然成立.若A与B均为幂零矩阵,即∃m,n∈N使得Am=0,Bn=0 可以得知(AB)k=(-1)k(k-1)/2AkBk=0,所以当m≤k或n≤k或者两者同时成立时,(AB)k=0成立,故AB是幂零矩阵.
由于A,B反可交换,所以AB+BA=0.同时由
A2B2=AABB=A(-BA)B
=BAAB=BA(-BA)=B2A2
可知A2,B2可交换.于是有:
(A+B)2k=[(A+B)2]k
=(A2+aB+BA+B2)k
=(A2+B2)k

故由Am=0,Bn=0,当mn≤k时,(A+B)2k=0,故A+B也是幂零矩阵,定理得证.
定理4若n阶矩阵A与B反可交换,则当n为奇数时,|A|=0或者|B|=0.
证明由矩阵A与B反可交换知AB=-BA,
|AB|=|A||B|,
|AB|=(-1)n|BA|=(-1)n|B||A|.
故当n为奇数时,有|A||B|=-|B||A|,即|A|=0或者|B|=0,定理得证.
定理5设矩阵A可逆,若矩阵A与B反可交换等价于矩阵A*与B反可交换.
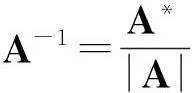
同理可证充分性,故定理得证.
下例表明:若矩阵A与B反可交换,则未必有矩阵A*与B反可交换.
例1 设

下例表明:设A与B为同阶矩阵,若A*与B反可交换,则未必有A与B反可交换.
例2 设
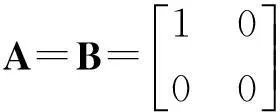
上面两个例子说明定理5中矩阵A可逆这个条件不能去掉.
定理6 设A,B为同阶可逆矩阵,则A,B反可交换的充要条件是(AB)*=-A*B*.
证明必要性:由A,B均为可逆矩阵可以得到均为可逆AB,BA,且(BA)-1=A-1B-1.再由A,B反可交换得:
(AB)-1=(-BA)-1=-A-1B-1,
从而由
得:
所以有(AB)*=-A*B*.
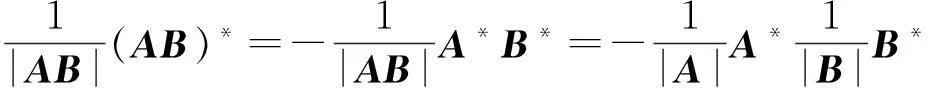
故A,B反可交换.
定理7 设A,B为同阶可逆矩阵,则A,B反可交换的充要条件是A*,B*反可交换.
证明 必要性:由A,B反可交换可得AB=-BA,再由A,B均可逆得A-1B-1=-B-1A-1.
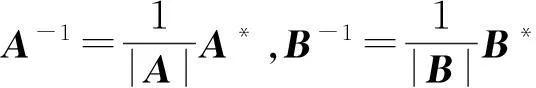

所以A*B*=-B*A*,故A*,B*反可交换.
充分性:由A*,B*反可交换得A*B*=-B*A*.
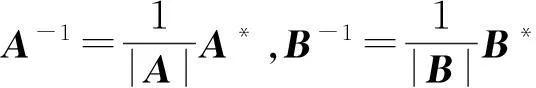
即A-1B-1=-B-1A-1.
从而得:(A-1B-1)-1=(-B-1A-1)-1,
故有BA=-AB,A,B,反可交换.
不妨假设矩阵A,B为同阶矩阵,显然(AB)T=(-BA)T是A,B反可交换的充要条件,当A,B均可逆时,(AB)-1=(-BA)-1是A,B反可交换的充要条件.下面讨论(AB)*=(-BA)*是否也为矩阵A,B反可交换的充要条件.
必要性显然成立.下面讨论充分性是否成立:
例3设矩阵

则(AB)*=(-BA)*,但是矩阵A,B不是反可交换的.因此,(AB)*=(-BA)*不是矩阵A,B反可交换的充分条件.
上例中A,B均不可逆,下例表明当矩阵A,B中有一个为可逆阵,另一个为不可逆阵时,(AB)*=(-BA)*也不是矩阵A,B反可交换的充分条件.
例4 设矩阵
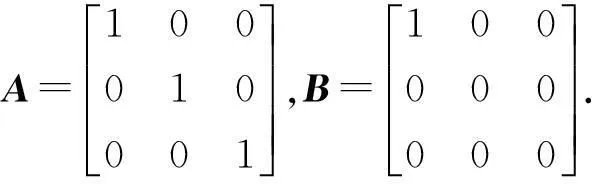
则有(AB)*=(-BA)*,但是矩阵A,B不是反可交换的.
下面考虑矩阵A,B均可逆时的情形.
例5 设矩阵
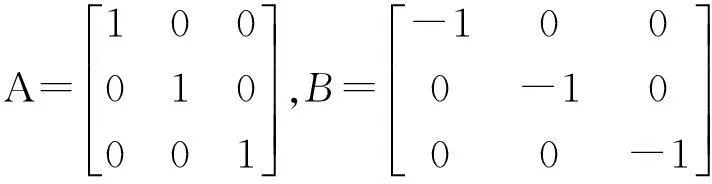
这说明当矩阵A,B均为可逆矩阵的时候,(AB)*=(-BA)*不是矩阵A,B反可交换的充分条件,但是当矩阵A,B均可逆且为偶数阶时,(AB)*=(-BA)*是矩阵A,B反可交换的充分条件:
定理8 设A,B为同阶可逆矩阵且阶数为偶数时,则A,B反可交换的充要条件是(AB)*=(-BA)*.
证明必要性显然,下证充分性.
充分性:由矩阵A,B为同阶可逆矩阵,并且阶数为偶数时有|AB|=|-BA|≠0,且有,
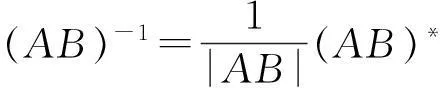
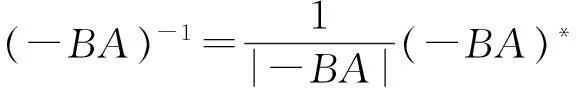
于是由(AB)*=(-BA)*有:
故有:
所以AB=-BA,即矩阵A,B为反可交换矩阵.
设A,B为n阶矩阵,可知:
(A-B)(A+B)=A2+2AB-B2A2-2BA-B2
或(A±B)2=A2+B2等均为A,B反可交换的充要条件.下面我们考虑(AB)2=-A2B2或(AB)2=(BA)2时,矩阵A,B是否反可交换问题.
显然A,B反可交换时有(AB)2=-A2B2,(AB)2=(BA)2,下面例子表明它们均不是A,B反可交换的充分条件.
例6 设

则AB=B,BA=0.
从而(AB)2=B2=O=-A2B2,
(AB)2=B2=O=(-BA)2.
而AB≠-BA,故有:
(AB)2=-A2B2,(AB)2=(BA)2,
但A,B不可反交换. 显然上述例子中矩阵A,B均不可逆.
下面考虑矩阵A,B恰有一个为可逆矩阵.
例7 设
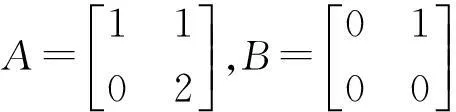
则有:
(AB)2=-A2B2=O,(AB)2=(BA)2=O
而AB≠-BA.这表明设A,B为同阶矩阵且恰有一个为可逆矩阵,则(AB)2=-A2B2不是A,B反可交换的充分条件,(AB)2=(BA)2也不是A,B反可交换的充分条件.
当A,B为同阶可逆矩阵时,若(AB)2=-A2B2,则有A-1(AB)2B-1=A-1(-A2B2)B-1,从而有BA=-AB,于是这时(AB)2=-A2B2是A,B反可交换的充分条件,于是有:
定理9 设A,B为同阶可逆矩阵,则反A,B可交换的充分必要条件是(AB)2=-A2B2.
例8 设

则A,B均可逆,且有:
(AB)2=(BA)2=-E,
AB=-BA,A,B反可交换.
例9 设

则A,B均可逆,且有(AB)2=(BA)2,但是AB=BA≠-BA,所以A,B不反可交换.
上例表明,当A,B均可逆时,(AB)2=(BA)2也不是A,B反可交换的充分条件.
参考文献:
[1]蔡晓静. 矩阵反可交换的条件及性质[J]. 高师理科学刊, 2012, 32(4): 22-24.
[2]戴立辉, 颜七笙, 刘龙章. 矩阵可交换的条件及可交换矩阵的性质[J]. 华东地质学院学报, 2002, 04: 353-355.
[3]唐建国. 与A可换矩阵空间的维数[J]. 河北师范大学学报:自然科学版, 1997, 21(1): 23-25.
[4]张禾瑞, 郝邴新. 高等代数[M].3版.北京: 高等教育出版社, 1983.
[5]唐建国, 杨振新. 与A反可换矩阵空间的维数[J]. 甘肃科学学报, 2006, 18 (1): 14-16.

Research on skew commutative matrix
YUAN Di, LIU Jia-qi
(School of Basic Science, Harbin University of Commerce, Harbin 150028, China)
Abstract:Some nature of the skew commutative matrix was given in this paper. And some necessary and sufficient conditions about some skew commutative matrixes were given.
Key words:matrix; skew commutative; invertible matrix
中图分类号:O211
文献标识码:A
文章编号:1672-0946(2016)01-0091-04
作者简介:袁笛(1991-),男,硕士,研究方向:微分方程反问题.
收稿日期:2015-06-14.
