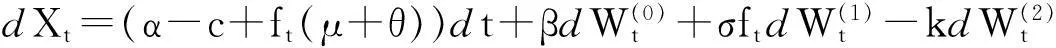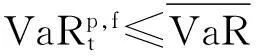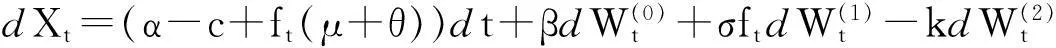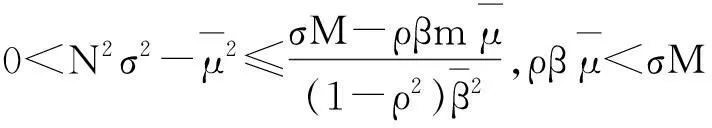保险公司VaR约束下的最优投资问题

王　珊(天津大学 理学院，天津 300072)



保险公司VaR约束下的最优投资问题

王珊(天津大学 理学院，天津 300072)

摘要：研究VaR约束下的具有随机现金流的保险公司投资问题.假设一个连续时间的金融市场存在一种无风险资产和一种风险资产.分别研究在仅有一种风险资产下的投资和在一种风险资产和无风险资产之间投资的问题.针对指数效用函数，在终端财富最大化的目标下，结合相应的VaR约束，通过建立和求解相应的HJB方程，得到相应问题的最优投资策略.

关键词：VaR约束；HJB方程；最优投资策略

如何合理运用暂时闲置的大量准备金是保险基金经营运作的重要的一个环节.投资能增加保险公司的收益，增强其赔付能力，减弱保险公司因巨额赔付而破产的可能性.

Browne[1]用连续的几何布朗运动模拟出保险公司的盈余过程，最早研究了指数效用函数最大化以及破产概率最小化目标下的最优投资策略问题.Hipp和Taskar[2]用复合Poisson模型模拟盈余过程，得到以最小化破产概率为目标的保险人的最优投资策略.Hipp和Plum[3]运用经典的Cramer-Lundberg模型刻画了保险盈余过程，假设保险基金仅投资于风险资产，当赔付分布是指数分布时，得到最优投资策略的显性表示.Liu和Yang[4]对该模型进行了改进，引入无风险资产，得到不同赔付分布下以最大化生存概率为目标的保险人最优投资策略的数值解.Yang和Zhang[5]将目标函数一般化，假设赔付过程是跳跃-扩散过程，用HJB方程研究了使保险人期望效用最大化的投资策略.Wang[6]利用不同方法将其推广到赔付过程是一般的单增纯跳跃过程，并指出最优投资策略与赔付过程无关.但上述研究多数仅考虑一种风险资产.Bai和Guo[7]将一种风险资产的投资推广到多个风险资产上，用HJB方程研究了最优比例再保险和投资的关系.

然而如果只考虑投资者的终端财富最大化，得出的投资决策往往会导致终端财富相当大的概率出现在取值较小的区域，这意味着最佳的终端财富可能会出现大的缺口风险.为了防止极端局面出现给投资者造成重大损失，本文考虑引入风险测量工具―在险价值(VaR)，限制暴露于市场中的风险.

VaR方法已为各领域的风险评估者所广泛使用，其是指在正常的市场条件和一定的置信水平下，某一证券组合在未来特定的一段时间内的最大可能损失.VaR衡量风险简单易操作，可事前计算风险，其易于计算组合风险的特点使得其在众多金融机构与监管机构中被广泛使用.

认识到限制风险通常不是一个投资者的主要目的， 投资者想限制他们的风险但希望预期效用最大化.这引出了在风险约束下的最优随机控制问题.Alexander和Baptista[8-9]研究了静态(单阶段)VaR与CVaR约束下的最优组合决策问题.Basak和Shapiro[10]通过加入在一个时间点上的约束限制研究了效用最大时的最优投资策略.Yiu[11]在全部资产上运用约束得到了最优交易策略. Pirvu[12]研究了约束下对数和指数效用下的最优投资和消费问题.

Cuoco[13]研究了风险约束下的投资者的动态连续情况下的投资策略.他假设投资者要满足连续的风险限制.Chen[14]研究了VaR约束下以最小破产概率为目标的保险公司的最优投资与再保险策略.Ye和Li[15]考虑了VaR约束下的最小均值―方差模型下的保险公司的最优投资问题.假设风险市场中只有一种风险资产可供投资者选择投资.而实际上，为使保险公司安全运行，往往要求其必须将部分资金投资于无风险资产上.

本文在Ye和Li的研究的基础上，扩充了资本市场资产的种类，考虑了当市场中拥有一种风险资产和无风险资产时的投资策略.同时考虑了两种特殊情形时的投资问题，包括Ye和Li的研究的仅投资于一种风险资产的情形，以及投资于一种风险资产与无风险资产时的情形.本文选择指数效用函数研究最大化财富终端问题.最大化财富终端效用满足投资者的收益最大的需求，VaR约束又限制了风险使其在投资者可接受的风险范围内.

1投资于一种风险资产和无风险资产时的投资模型

1.1连续时间投资模型

本文假设所有的随机过程都适应于过滤空间(Ω，F，Ft,P)，这里Ft是通常概率空间中的过滤.

本文假设市场中仅有一种风险资产和一种无风险资产可供选择，其中无风险资产包括债券或银行账户，风险资产包括股票或基金.假设初始时刻为0，终止时刻为T.无风险资产价格为Bt，且满足如下方程：

dBt=r0Btdt

(1)

这里r0是无风险利率.

风险资产价格分别为St，服从几何布朗模型：

(2)

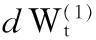
将公司的资产看成一个随机现金流，相应的问题简化为在随机现金流的基础上的投资问题.假设公司在t时刻的资产(即随机现金流)为Vt，它可以用带漂移率α，扩散系

(3)

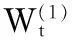
将保险公司的消费也同样看成一个随机过程，记为：

(4)

这里c>0；k>0.假设消费过程与盈余过程和投资问题之间没有联系.

(5)

1.2在险价值(VaR)

(6)

为了得到Xt+τ-Xt，将式(6)改写为积分形式

(7)

这里x > 0为资产的最初价值，由式(7)有

(8)

假设投资策略在[t,t+τ]内为固定的，即投资于风险资产fs≡f.

由式(8)得，在给定[t,t+τ]固定的投资策略f和时刻t的资产价值Xt=X的情况下，

(9)

命题1(VaR的计算)

(10)

这里Φ和Φ-1(.)为标准正态分布及其逆分布.

命题的证明：

P(Xt+τ-Xt≤L|Ft)

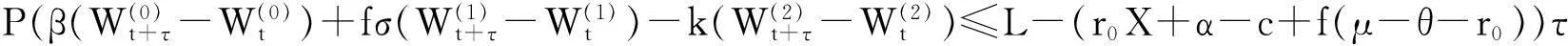
这里

Z=

经整理有，

1.3问题的阐述

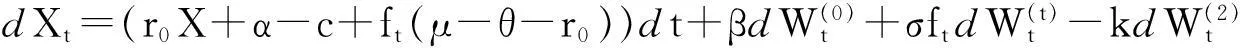
(11)

取效应函数为保险数学中常用的指数函数

(12)

命题2(VaR约束的计算)满足式(11)中VaR约束的f为：

(13)

命题的证明：

要计算出满足以下VaR约束的f：

等价于计算

将方程改写为

(14)

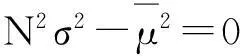
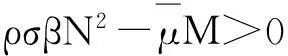
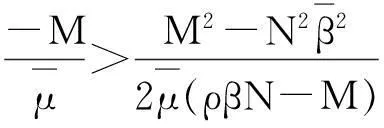
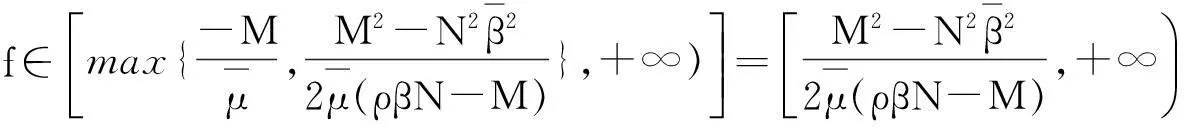
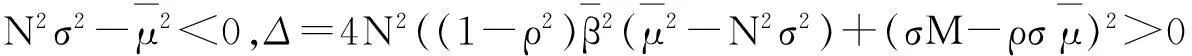
方程有两个相异的解，分别为

1.4无约束时的投资策略

在无VaR约束时，只需解决

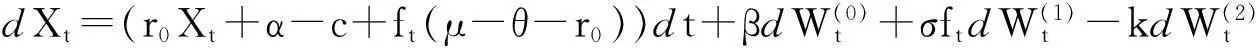
(15)

定理1在没有VaR约束情况下，t时刻终端财富最大的最优策略为

(16)

公司最优价值为

(17)

其中

(18)

定理的证明：由Fleming和Rishel，相应的HJB方程可写为：

(19)

为求解最优投资策略f*，可对f求一阶偏导，

(20)

将式(20)代入式(1)，有

(21)

积分，并考虑初值h(0)=0.可得式(18).再将Vx，Vxx代入f*，得到最优投资策略.

1.5带有VaR约束的最优投资问题

(22)

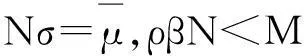
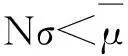
(23)

由于情况1)概率较小，且与情况2)、3)具有相似性，所以我们仅求解情况2)、3).由上述分析可知，当f*∈[f2,+∞)时，最优投资策略仍为f*，计算不用重复.现只需将时f

将f2代入式(19)有，

其中，λ>0,γ>0,θ>0.分别对其求关于x,t的偏导数，代入上述方程有：

(at+r0a(t))x+ht+F1a(t)-G1θa2(t)=0

由分立变量法，对任意x等式都成立，将等式分解成两部分，解出

同理可求得情况3)的解.所以情况2)、3)的投资价值方程为：

V(t,x)=

V(t,x)=

2仅有一种风险资产的投资模型

2.1连续时间投资模型

假设市场中只有一项风险资产可供选择，其中风险资产包括股票或基金.假设初始时刻为0，终止时刻为T.因此投资者的财富过程为：

(24)

2.2在险价值(VaR)

命题1(VaR的计算)

(25)

这里Φ(·)和Φ-1为标准正态分布及其逆分布.

2.3问题的阐述

可以将问题描述为：

(26)

取效应函数为指数函数，形式如式(12).

命题2(VaR约束的计算)满足(26)中VaR约束的f为：

(27)

2.4无VaR约束时的投资策略

在无约束时，只需解决

(28)

定理3使得中观财富最大的t时刻最优策略为

(29)

公司最有价值为

(30)

其中

(31)

2.5带有VaR约束的最优投资问题

(32)

由于情况一概率较小，且与情况二三具有相似性，所以我们仅求解情况二三.由上述分析可知，当f*∈[f2,+∞)时，最优投资策略仍为f*，计算不用重复.现只需将f

整理方程，有

应用傅里叶变换，将终端财富化为初始财富，有：

假设解的形式为V(t,x)=(x-a)2+Axt+Bt2+Ct，分别求关于x,t的偏导数，解出

同理可求得情况3)的解.所以最优投资方程为

V(t,x)=

V(t,x)=

其中h(T-t)形式如式(31).

3结语

现有对保险公司的研究多集中于投资与再保险策略的研究，但是多数仅以终端财富效应最大化为目标函数，很少考虑到将最小化风险作为选择最优投资策略的必要条件.本文在最小化VaR风险下约束下，针对指数效用, 在最大化终端财富目标下，探讨了保险公司最优投资策略，还有进一步改进的地方， 比如用其他风险测度方法表示风险，如CVaR，TCE条件下的最优投资策略.还可以同时考虑再保险政策，分红政策等，使研究更为丰富，更贴近实际.

参考文献：

[1]BROWNES.OptimalInvestmentPoliciesforaFirmwithaRandomRiskProcess:ExponentialUtilityandMinimizingtheProbabilityofRuin[J].MathematicsofOperationsResearch, 1995, 20: 937-958.

[2]HIPP C, TASKAR M. Stochastic control for optimal new business [J]. Insurance: Mathematics and Economics, 2000, 26: 185-192.

[3]HIPP C, PLUM M. Optimal Investment for Insurers [J]. Insurance: Mathematics and Economics, 2000, 27: 215-228.

[4]LIU C S, YANG H. Optimal Investment for an Insurer to Minimize its Probability of Ruin [J]. North American Actuarial Journal, 2004, 8: 11-31.

[5]YANG H, ZHANG L. Optimal Investment for Insurer with Jump-diffusion Risk Process [J]. Insurance: Mathematics and Economics, 2005, 37: 615-634.

[6]WANG N. Optimal Investment for an Insurer with Exponential Utility Preference [J]. Insurance: Mathematics and Economics, 2007, 40: 77-84.

[7]BAI L H, GUO J Y. Optimal proportional reinsurance and investment with multiple risky assets and no-shorting constraint [J]. Insurance: Mathematics and Economics, 2008, 42: 968-975.

[8]ALEXANDER G J, BAPTISTA A M. A comparison of VaR and CVaR constraints on portfolio selection with the mean-variance model [J]. Management Science, 2004, 50(9): 1261-1273.

[9]ALEXANDER G J, BAPTISTA A M, YAN S. Mean-variance portfolio selection with ‘at-risk’ constraints and discrete distributions [J]. Journal of Banking & Finance, 2007, 31(12): 3761-3781.

[10]BASAK S, SHAPIRO A. Value-at-risk-based risk management: optimal policies and asset prices [J]. Review of Financial studies, 2001, 14(2): 371-405.

[11]YIU K F C. Optimal portfolios under a value-at-risk constraint [J]. Journal of Economic Dynamics and Control, 2004, 28(7): 1317-1334.

[12]PIRVU T A. Portfolio optimization under the value-at-risk constraint [J]. Quantitative Finance, 2007, 7(2): 125-136.

[13]CUOCO D, HE H, ISAENKO S. Optimal dynamic trading strategies with risk limits [J]. Operations Research, 2008, 56(2): 358-368.

[14]WANG Z R, CHEN X H, JIN Y B,etal. Estimating risk of foreign exchange portfolio: Using VaR and CVaR based on GARCH-EVT-Copula model[J]. Physica A: Statistical Mechanics and its Applications, 2010, 389(21): 4918-4928.

[15]YE Y, LI T. The optimal mean-variance investment strategy under value-at-risk constraints [J]. Insurance: Mathematics and Economics, 2012, 51(2): 344-351.

Optional investment problem of insurance company underVaRconstraints

WANG Shan

(School of Science, Tianjin University, Tianjin 300072, China)

Abstract：In this paper, the investment problem of the insurance company which has stochastic cash flow under the VaR constraints was studied. Assumed that there was a riskless asset and a risky asset in the financial market and the financial market was a continuing market.In this paper the problem of investment were studied in two cases. One was that there was only one risky asset in the market and the other was that there was a riskless asset and a risky asset in the market. According to the exponential utility function and the goal of maximizing the terminal wealth,get the optimal investment strategy by establishing and solving the corresponding HJB equation under the corresponding VaR constraints.

Key words：VaR constraints; HJB equation;optional investment strategy

中图分类号：O29

文献标识码：A

文章编号：1672-0946(2016)01-0112-07

作者简介：王珊(1989-)，女，硕士，研究方向：金融数学.

收稿日期：2014-12-23.