面向空间信息传输的骨干网络容量模型

张　平，秦智超，陆　洲

(中国电子科学研究院，北京　100041)

张　平(1981—)，男，浙江临海人，博士，主要研究方向为空间信息网络、天地一体化网络：

E-mail：zhangping1224@gmail.com

秦智超(1981—)，男，河北沧州人，博士，主要研究方向为无线网络；

陆　洲(1970—)，男，河北人，研究员级高级工程师，主要研究方向为宽带卫星通信、天基网络。



工程与应用

面向空间信息传输的骨干网络容量模型

张平，秦智超，陆洲

(中国电子科学研究院，北京100041)

摘要：空间骨干网络是空间网络的核心，本文面向空间信息传输的应用场景，提出了空间骨干网络容量的理论分析模型。基于空间骨干节点是否与地面站直接相连，该模型区分了空间两类不同的节点：普通节点和枢纽节点，并据此分析网络容量的关键瓶颈和理论上限。通过将该模型应用到具体网络拓扑中，可以计算网络容量、找出网络关键链路并给出拓扑优化方案。计算结果表明，对于6个节点的空间骨干网络，经过拓扑优化之后，在两种不同假设条件下网络容量可以分别提升33.3%和100%。

关键词：空间信息传输；空间骨干网络；网络容量；拓扑优化

0引言

空间网络是由各种空间节点(包括同步轨道、中低轨道航天器以及临近空间飞行器等)以及相应的地面设施构成的一张立体化网络。相比地面网络，空间网络在覆盖范围、网络生存性等方面都有独特的优势，在空间信息传输、应急救援、航空运输、远洋航行、空间探索等领域发挥不可或缺的作用。

空间信息传输是空间网络的重要应用之一。根据美国UCS网站上的统计数据[1]，截止2015年8月底，我国在轨卫星有142颗，其中对地观测类(包括遥感、气象、海洋、环境、资源等系列)卫星有70颗，占了将近一半。这些卫星在运行的每时每刻都会生成大量的信息，因为星上在轨信息处理能力有限，大部分空间信息需要传回地面处理，这对空间网络尤其是空间骨干网络的传输能力带来了很大的挑战。

在空间信息传输中，空间骨干网起到了核心的作用，一般由比较稳定的同步轨道卫星组成[2]，通过星间和星地高速链路提供空间宽带传输。对于骨干网络来说，网络容量是其重要的性能评价指标。本文主要面向空间信息传输的应用场景，提出了一种空间骨干网络容量的理论分析模型，根据该模型计算网络容量的上限，并且给出网络拓扑优化的方案。

1相关工作

通常所说的容量有两类：链路容量和网络容量，其中链路容量只是对点对点链路传输性能的描述，而网络容量描述的是整个网络的性能，即网络能够承载的最大业务量，本文主要关注网络容量的研究。

地面网络的网络容量研究已经比较充分，包括无线网络和有线网络。在地面无线网络中[3,4]，受无线信道的广播特性和传输距离的限制，网络容量与节点的数量和位置分布密切相关。在地面有线网络中[5]，网络容量与网络结构和路由策略有关。网络容量的计算基本采用数值模拟的方式[6,7]，通过不断增加网络输入的业务量，直至网络中某条链路达到满载。

空间骨干网络研究主要集中在链路技术和组网技术。其中链路技术主要是高速空间激光传输技术[8-10]，包括星间和星地激光通信，经过一系列在轨试验之后，技术上趋于成熟，是构建空间骨干网络的基础。空间组网技术包括星座设计和网络拓扑优化[11-13]，基于网络容量、时延、生存性进行多目标优化设计，计算复杂度高。

本文的主要工作是针对空间信息传输的具体应用场景，并根据空间骨干节点是否与地面站直接相连把所有节点区分为普通节点和枢纽节点两大类，从而简化网络模型，并在此基础上提出了网络容量的理论分析模型。

2空间骨干网络容量模型

同步轨道(Geosynchronous Earth Orbit，GEO)卫星距离地面约3.6万公里，轨道周期与地球自转周期恰好相同，所以与地面保持相对静止，并且覆盖范围广，是空间骨干网络的理想选择。如图1所示，空间骨干网络由数颗GEO骨干卫星组成，相互之间通过星间链路组网，实现全球范围内的空间信息传输。同时在地面布设卫星地面站，通过星地链路接收位于其上方的GEO卫星传输的空间信息。

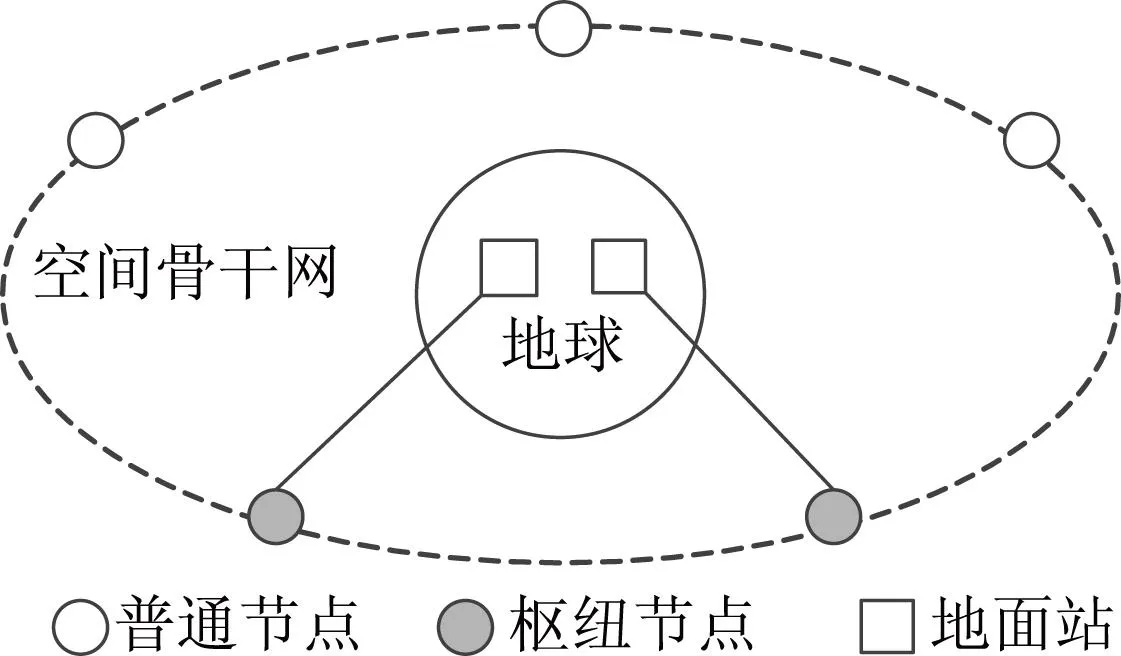
图1　空间骨干网络示意图

受地理条件和成本限制，一般没法做到每一颗GEO骨干卫星都对应一个地面站，只有一部分GEO卫星可以与地面站建立直接的传输通道，剩余部分的GEO卫星必须要经过前者的中转才能把信息传回地面。为了便于区分，将前者称为枢纽节点，后者称为普通节点。

假设整个空间骨干网络有N个骨干卫星节点，其中普通节点和枢纽节点个数分别为No和Ns，分别记为O1，O2，…，ONo以及S1，S2，…，SNs。另外，地面上有Ns个地面站，与天上的Ns枢纽节点一一对应，记为G1，G2，…，GNs。

空间骨干节点中，节点i(1≤i≤N)需要传输的空间信息业务量为ci，定义总容量C=c1+c2+…+cN，其中各节点业务量比例系数λi=ci/C。

空间骨干节点间的星间链路容量矩阵为R={rij}，1≤i,j≤N，其中rij代表从节点i到节点j的星间链路容量。针对普通节点和枢纽节点的区别，可以将容量矩阵细分为三个子矩阵：①普通节点内部的容量矩阵R1={rij}，1≤i,j≤No；②普通节点到枢纽节点的容量矩阵R2={rij}，1≤i≤No，No+1≤j≤N；③枢纽节点内部的容量矩阵R3={rij}，No+1≤i,j≤N，用矩阵形式表示如下：

(1)

因为不存在从枢纽节点到普通节点的空间信息流向，所以对应的链路容量矩阵为0。

枢纽节点与地面站之间是一对一的星地链路，链路容量Q={qi}，1≤i≤Ns，其中qi代表从枢纽节点Si到地面站Gi的星地链路容量。

整个网络的信息流向如图2所示，枢纽节点的业务可以直接传给地面站，但普通节点的业务必须经过枢纽节点中转才能传回地面。

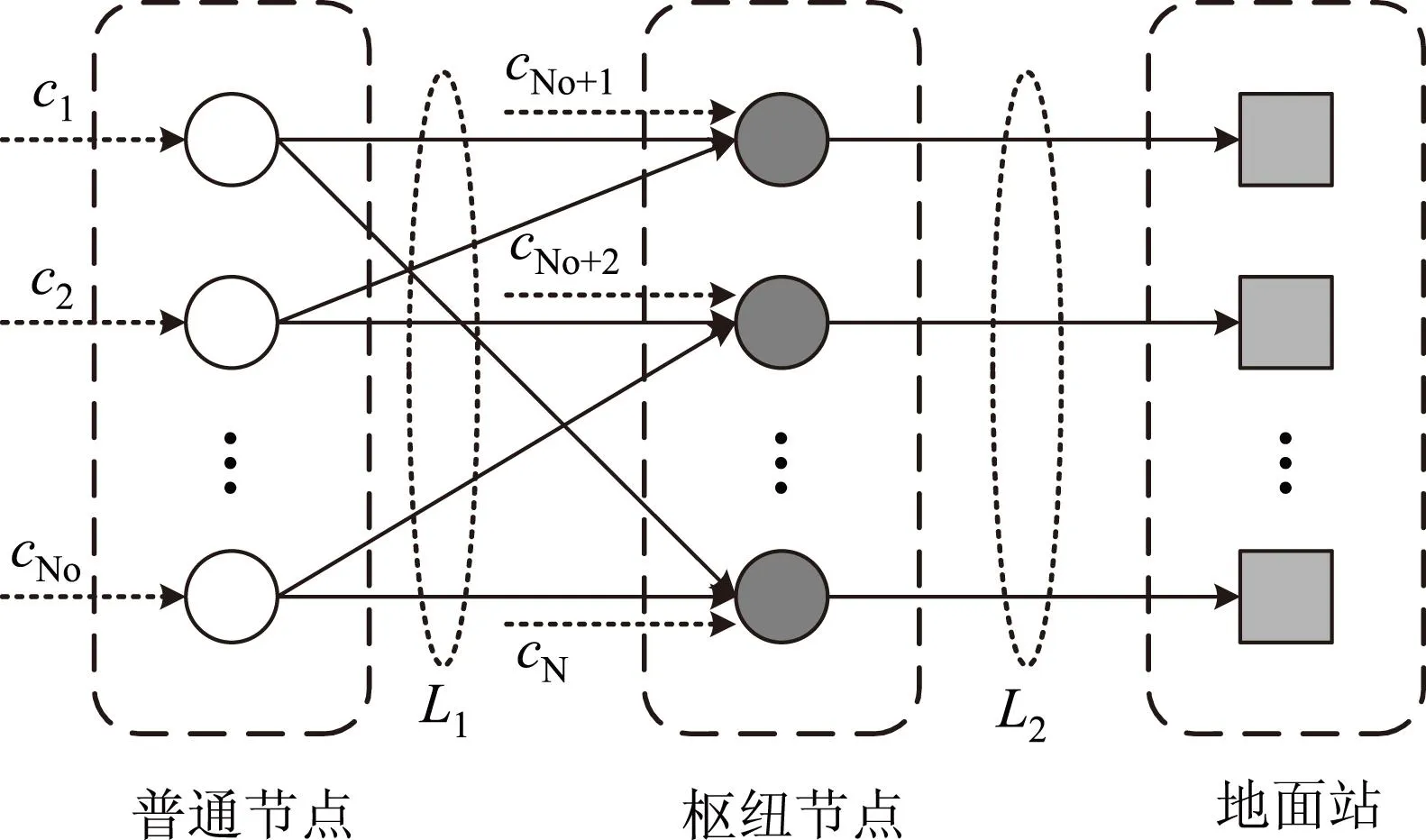
图2　空间骨干网络拓扑结构图

通过对图2所示的网络拓扑结构分析，可以发现有两个关键的网络瓶颈限制了整个网络的总容量，分别是普通节点到枢纽节点之间的所有链路总容量L1，枢纽节点到地面站之间的链路总容量L2。给定星间链路容量矩阵R和星地链路容量Q之后，可以计算出L1和L2的值：

(2)

(3)

从信息流的角度可以得出，普通节点能够传输到枢纽节点的业务量不会超过L1，枢纽节点能够传输到地面站的业务量不会超过L2，即：

(4)

(5)

由以上两式可以得到网络容量C的上限：

(6)

可以看到，要提高网络容量C，需要尽可能提高L1和L2的值，并使得两者的比值与业务量比例相符，下面两小节将分别就这两部分的容量展开分析。

2.1普通节点到枢纽节点的容量分析

问题描述：网络中有No个普通节点和Ns个枢纽节点，分别记为：O1，O2，…，ONo和S1，S2，…，SNs，已知普通节点输入的业务量C1={c1，c2，…，cNo}，普通节点内部链路容量矩阵R1和普通节点到枢纽节点链路容量矩阵R2，目标是使得普通节点到枢纽节点传输的业务总容量达到最大，即：

(7)

受节点间物理距离和收发器数量等因素的制约，有些普通节点跟枢纽节点间没有直连的链路，并且不同普通节点到枢纽节点间的链路能力也不同，所以在普通节点内部需要有一个交换网络来完成业务量在网络内部各节点的再分配，如图3所示。

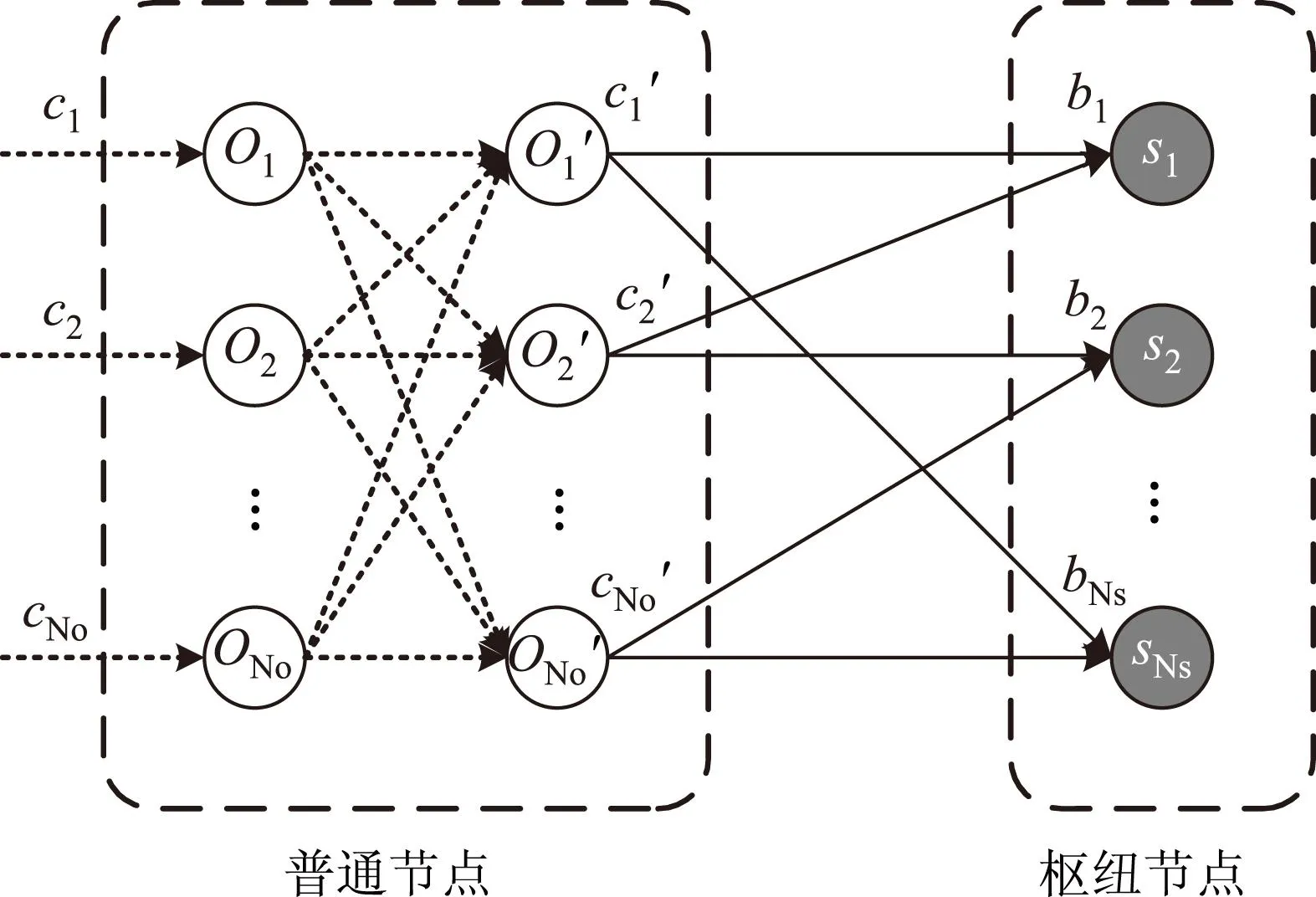
图3　普通节点到枢纽节点连接拓扑图

为了清楚区分起见，分别用O1，O2，…，ONo和O1′，O2′，…，ONo′代表交换前后的节点，经过内部网络交换之后的业务量为C1′={c1′，c2′，…，cNo′}，把交换前后的业务量C1和C1′分成共同部分和差异部分：其中共同部分不需要交换，记为C0={c0,1，c0,2，…，c0,No}，计算如下：

(8)

差异部分才是真正需要在内部交换的业务，记为D1={d1，d2，…，dNo}和D1′={d1′，d2′，…，dNo′}，计算如下：

(9)

(10)

交换前后总业务量保持不变，即：

(11)

另外，在网络中传输的业务量不能超过链路的容量，即：

(12)

(13)

内部交换完成之后的普通节点业务再经过矩阵交换传输到枢纽节点，输入到枢纽节点的业务量为B1={b1，b2，…，bNs}，C1’和B1的关系如下：

(14)

(15)

2.2枢纽节点到地面站的容量分析

问题描述：网络中有Ns个枢纽节点以及与之相对应的Ns个地面站，分别记为：S1，S2，…，SNs和G1，G2，…，GNs，已知枢纽节点的输入业务量E1={e1，e2，…，eNs}，枢纽节点内部链路容量矩阵R3和枢纽节点到地面站链路容量Q，目标是使得枢纽节点到地面站传输的业务总容量达到最大，即：

(16)

枢纽节点的业务量E1包括两部分：自身需要传输的业务量C2={cNo+1，cNo+2，…，cN}和来自普通节点输入的业务量B1={b1，b2，…，bNs}，即：

(17)

跟上一节的分析一样，枢纽节点先在内部之间完成业务量的再分配，使得每个枢纽节点的业务量与它跟地面站的链路能力相匹配，如图4所示。

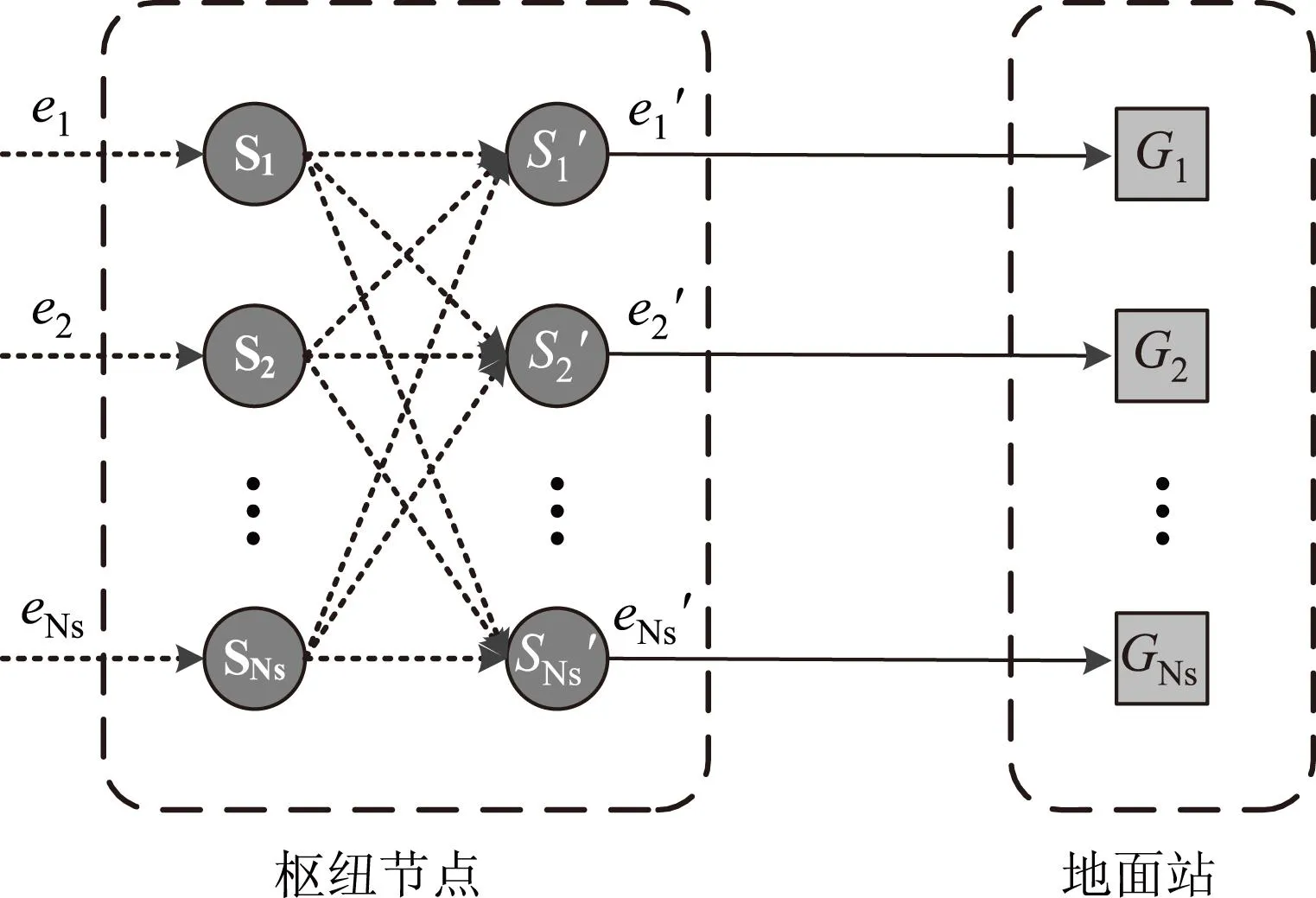
图4　枢纽节点到地面站连接拓扑图

为了清楚区分起见，分别用S1，S2，…，SNs和S1′，S2′，…，SNs′代表交换前后的节点，经过内部网络交换之后的业务量为E1′={e1′，e2′，…，eNs′}，把交换前后的业务量E1和E1’分成共同部分和差异部分：其中共同部分不需要交换，记为E0={e0,1，e0,2，…，e0,Ns}，计算如下：

(18)

差异部分才是真正需要在内部交换的业务，记为F1={f1，f2，…，fNo}和F1′={f1′，f2′，…，fNo′}，计算如下：

(19)

(20)

交换前后总业务量保持不变，即：

(21)

另外，在网络中传输的业务量不能超过链路的容量，即：

(22)

(23)

内部交换完成之后的枢纽节点将业务发给对应的地面站，满足如下关系：

(24)

3空间骨干网络容量计算及拓扑优化

根据上面的容量模型，本节将针对具体的网络实例进行网络容量的计算以及拓扑的优化。

3.1网络容量计算

假设有一个由6个节点的空间骨干网络，其中普通节点三个(O1,O2,O3)，枢纽节点三个(S1,S2,S3)，与之对应的地面站有三个(G1,G2,G3)，有6条星间链路和3条星地链路，网络拓扑如图5所示。

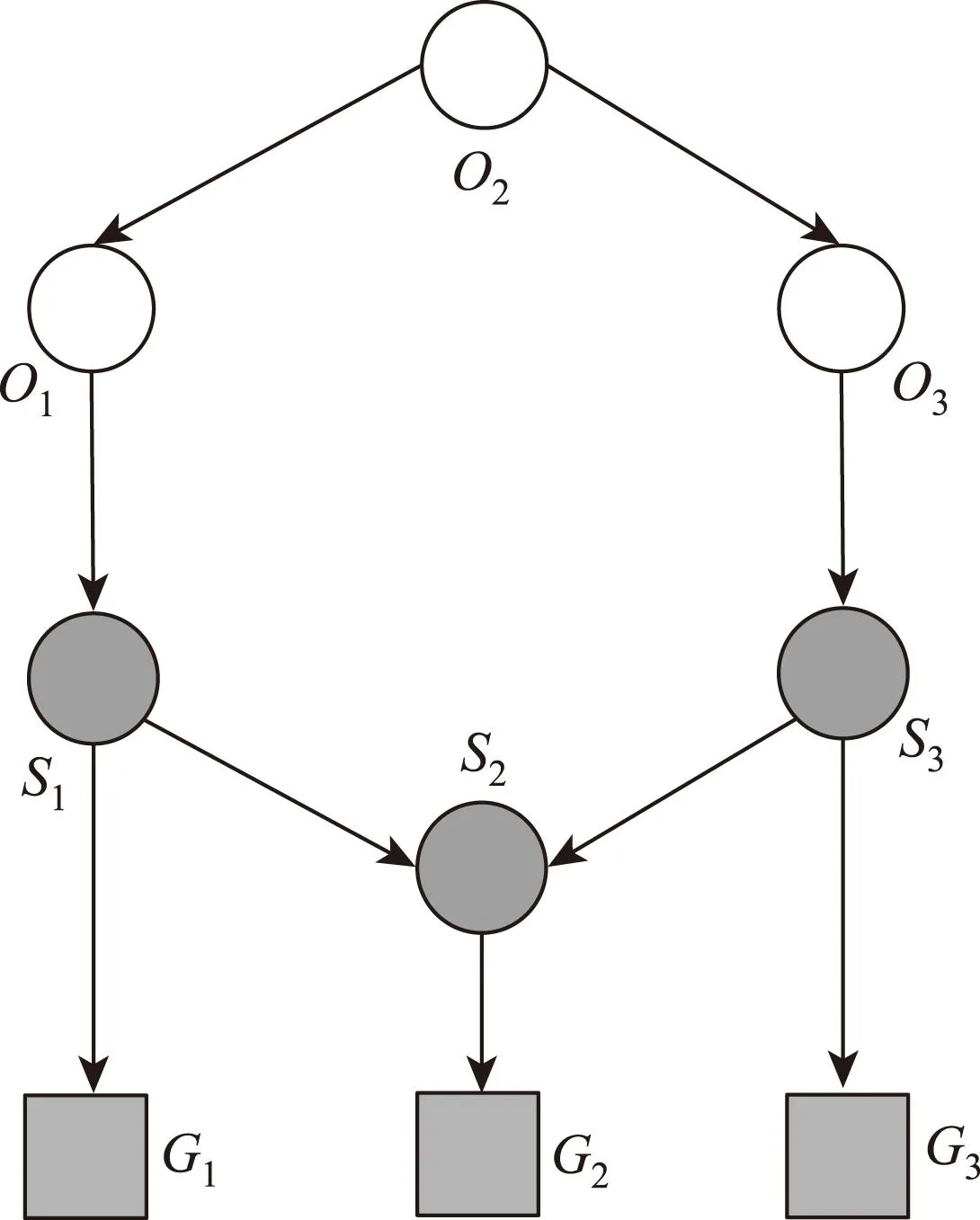
图5　空间骨干网络示例

不失一般性，假设所有星间和星地链路的容量均为1个单位，由此可以得到链路容量矩阵R和Q：

(25)

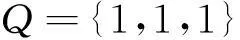
(26)

再根据公式(2)和(3)，可以计算出L1和L2的值：

L1=2

(27)

L2=3

(28)

假设每个空间节点的业务量相同，即：

(29)

代入公式(6)可以得出网络容量C的上限：

C≤3

(30)

公式(30)表示在图5所示的网络拓扑下，网络容量最大为3个单位，下面将计算如何分配业务流量使得网络容量达到其最大值。

首先，网络总容量为3个单位，可以计算出每个节点的业务量为：

(31)

普通节点和枢纽节点的业务量分别为：

(32)

(33)

根据公式(24)，每个枢纽节点输出到地面站的业务量不超过链路容量(1个单位)，为了实现容量最大，每条链路的容量都需占满，即：

(34)

在枢纽节点的输入端，每个枢纽节点自身都有业务量1/2单位，同时枢纽节点S1和S3还有来自普通节点的总计为3/2单位(3个节点)的业务量，均分到两个节点，可以得到：

(35)

(36)

(37)

(38)

分别都满足公式(22)和(23)的要求。

从公式(35)，再结合公式(14)和(15)，可以得到普通节点输出到枢纽节点的业务量：

(39)

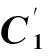
(40)

(41)

分别都满足公式(12)和(13)的要求。

图6给出了网络总容量为3个单位(即每个节点业务量为1/2单位)时，整个网络的业务分配和每条链路上的业务负载情况。可以发现，不同链路的负载很不均衡，有些链路(比如星地链路)已经达到满载，但也有些链路(比如节点O2到O1)的负载很小，表明整个网络拓扑有进一步优化的空间，从而实现网络容量的整体提升。

图6　网络业务负载情况

3.2网络拓扑优化

本小节针对上面的网络实例(如图5所示)进行拓扑优化，以提高网络的总容量，优化过程中以下基本假设条件保持不变：

● 空间6个节点：3个普通节点和3个枢纽节点，每个节点业务量相同；

● 地面3个地面站与枢纽节点一一对应；

● 总共9条星间或星地链路。

其中星地链路容量设为1个单位，而对于星间链路容量，根据链路容量是否与距离相关作了两种不同的假设，并分别展开优化设计：

(1)星间链路容量固定

假设所有的星间链路容量都固定为1个单位，在这种情况下调整网络中9条星间或星地链路的位置，使得整个网络的容量达到最大。

优化的方法是尽可能的提高L1和L2的值，也就是减少普通节点内部以及枢纽节点内部的链路数量，增加普通节点到枢纽节点以及枢纽节点到地面站之间的链路数量，同时调整L1和L2的比例与业务量相匹配，使得每条链路上的业务负载量尽可能均衡。

理想情况下，普通节点内部和枢纽节点内部无链路相连，所有链路都用于普通节点到枢纽节点(L1)以及枢纽节点到地面站(L2)之间，即

L1+L2=9

(42)

另一方面，根据公式(6)，L1和L2的比值要与业务量匹配，即

(43)

由公式(42)和(43)可以得出：

L1=3

(44)

L2=6

(45)

也就是说经过优化之后，9条链路有3条位于普通节点到枢纽节点之间，有6条位于是枢纽节点到地面站之间。

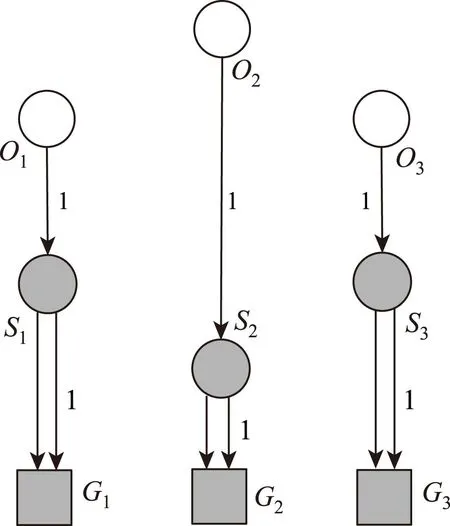
图7　优化后的网络拓扑图及业务负载情况(假设1)

图7给出了一个优化后的网络拓扑以及每条链路上的业务负载情况，其中每个普通节点与1个枢纽节点建立1条一对一的星间链路，负责传输来自普通节点的业务，而每个枢纽节点与对应地面站则有2条星地链路，负责传输枢纽节点自身以及来自普通节点的总计两个节点的业务量。经过优化后，每个节点最大可传输业务量为1个单位，整个网络的总容量为6个单位，比优化前的网络容量提升了一倍(100%)。

(2)星间链路容量与距离相关

在实际系统中，链路的容量与传输距离密切相关，在自由空间传输的损耗与距离的平方成反比，因此在发射功率和接收灵敏度给定的条件下，链路容量(最大传输速率)与传输距离的平方成反比。假设6个节点在同步轨道上均匀分布，相邻两个节点(比如O1和O2)的链路容量为1个单位，其它节点间的链路容量可根据对应距离计算出来，具体每条星间链路的容量如表1所示。

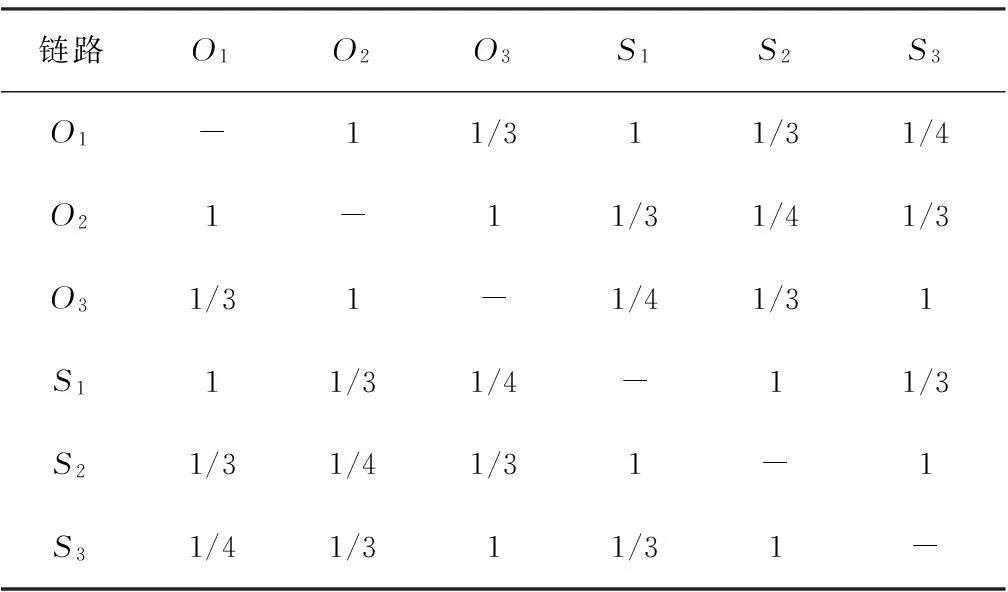
表1　不同节点间的星间链路容量

在这种情况下，图7就不是最优的网络拓扑了，由于链路O2到S2的容量只有1/4单位，导致整个网络的容量只有3/2单位，甚至还不如优化前图5所示的网络。

由于链路容量与距离的平方成反比，网络传输的瓶颈处于距离枢纽节点最远的节点(即O2)，在距离远的情况下传输同样的业务就需要多分配链路资源。从表1可以看到，普通节点O2到三个枢纽节点S1、S2、S3的链路容量分别为1/3、1/4、1/3单位，最大才1/3单位，而O1到S1、O3到S3的容量为1单位，要满足各个节点传输业务的均衡，至少要给O2分配两条以上的链路与枢纽节点相连。

最终优化后的网络拓扑和业务负载情况如图8所示，其中普通节点O2有2条星间链路，分别连接到枢纽节点S1和S3，每个节点的最大可传输业务量为2/3单位，整个网络容量为4个单位，比优化前的网络容量提升了1/3(33.3%)。

图8　优化后的网络拓扑图及业务负载情况(假设2)

4结语

针对空间信息传输的网络应用场景，本文提出了空间骨干网络容量的分析模型。通过该模型可以计算任意网络拓扑的网络容量上限，并给出具体的网络流量分配以达到该上限值。同时，该模型也可用于指导网络拓扑的优化设计，在保持链路数不变的情况下提高网络的容量。对于空间6个节点的骨干网络，在两种假设情况下，经过拓扑优化之后网络容量都得到了显著提升，提升幅度分别达到33.3%和100%。

参考文献：

[1]http://www.ucsusa.org/nuclear_weapons_and_global_security/solutions/space-weapons/ucs-satellite-database.html, 2015/9/1.

[2]张乃通, 赵康僆, 刘功亮. 对建设我国“天地一体化信息网络”的思考[J]. 中国电子科学研究院学报, 2015, 10(3): 223-230.

[3]P. Gupta and P. R. Kumar, “The capacity of wireless network”, IEEE Transaction on Information Theory, vol. IT-46, no. 2, pp. 388-404, 2000.

[4]L. Pan, Z. Chi and F. Yuguang, “Capacity and delay of hybrid wireless broadband access networks”, IEEE Journal on Selected Areas in Communication, vol. 27, pp. 117-125, 2009.

[5]Z. Y. Chen and X. F. Wang, “Effects of structure and routing strategy on network capacity”, Physical Review E., vol.73, pp. 100-107, 2006.

[6]Q. Yingzhen and P. K. Verma, “Limits on the traffic carrying capacity of optical networks with an arbitrary to-pology”, IEEE Communications Letters, vol. 8, pp. 641-643, 2004.

[7]Z. Jingjing and N. Ansari, “On the capacity of WDM Passive Optical Network”, IEEE Transaction on Communications, vol. 59, pp. 552-559, 2011.

[8]Vincent W. S. Chan,“Free-Space Optical Communications”, Journal of Lightwave Technology, vol. 24, no. 12, pp.4750-4762, 2006.

[9]P. Hopman, P.W. Boettcher, L.M. Candell, J. B. Glettler, and R. C. Shoup,“An end-to-end demonstration of a receiver array based free-space photoncounting communications link,” in SPIE Free Space Laser Commun. VI.Bellingham, WA: SPIE, Aug. 2006.

[10]S. Seel, H. Kampfner, F. Heine, D. Dallmann, G. Muhlnikel, M. Gregory, M. Reinhardt, K. Saucke, J. Muckherjee, U. Sterr, B. Wandernoth, R. Meyer, and R. Czichy, “Space-to-ground bidirectional optical communications link at 5.6 Gbps and EDRS connectivity outlook,” paper 1111, IEEE Aerospace Conf. Proc., Big Sky, MT, Mar. 5-12, 2011.

[11]Jason H. Bau,“Topologies for Satellite Constellationsin a Cross-Linked Space BackboneNetwork”,Thesis, Massachusetts Institute of Technology, 2002.

[12]Serena Chan, and Vincent W.S. Chan,“ConstellationTopologies for a Space-Based Information Network Backbone Using Optical Intersatellite Links”, MILCOMM 2004, pp 812-821, 2004.

[13]Mark D. Johnston, “An EvolutionaryAlgorithm Approach to Multi-Objective Scheduling of Space Network Communications”, Intelligent Automation and Soft Computing, Vol. 14, No. 3, pp. 367-376, 2008.

张平(1981—)，男，浙江临海人，博士，主要研究方向为空间信息网络、天地一体化网络：

E-mail：zhangping1224@gmail.com

秦智超(1981—)，男，河北沧州人，博士，主要研究方向为无线网络；

陆洲(1970—)，男，河北人，研究员级高级工程师，主要研究方向为宽带卫星通信、天基网络。

An Analytical Model of Space Backbone Network Capacity for Space Information Transmission

ZHANG Ping, QIN Zhi-chao, LU Zhou

(China Academy of Electronics and Information Technology, Beijing 100041, China)

Abstract:The space backbone network is the core of space networks, concerning the application scenario of space information transmission, an analytic model of space backbone network capacity was proposed in this paper. The analytic model discloses the bottle neck and upper bound of the network capacity, by distinguishing two different types of the space nodes: the ordinary nodes and the key nodes, based on whether the space backbone node is directly connected with the earth station. By applying the model to some-concrete network topology,we could calculate the network capacity,find out the critical path sand propose topology optimization solutions. Numerical results show that,for a space-based backbone network with six nodes,after the topology optimization with two different assumptions, the network capacity can be improved by 33.3% and 100% respectively.

Key words:space information transmission; space backbone network; network capacity; topology optimization

作者简介

中图分类号：TP393

文献标识码：A

文章编号：1673-5692(2016)01-066-07

基金项目：国家自然科学基金资助项目(91338201)，国家863计划资助项目(2015AA015701)

收稿日期：2015-11-30

修订日期：2016-01-11

doi:10.3969/j.issn.1673-5692.2016.01.013