浮标布阵投放航线实验与误差分析

蔡爱华，何建伟，王　鹏

(中国电子科学研究院，北京　100041)

蔡爱华(1962—)，男，江苏盐城人，中国电子科技集团公司首席专家，研究员级高工，主要研究方向为机载电子信息系统；

E-mail：caiaihua62@163.com

何建伟(1982—)，男，海南儋州人，工学博士，高级工程师，主要研究方向为机载电子信息系统总体技术；

王　鹏(1990—)，男，陕西富平人，硕士，助理工程师，主要研究方向为机载电子信息系统总体技术。



工程与应用

浮标布阵投放航线实验与误差分析

蔡爱华，何建伟，王鹏

(中国电子科学研究院，北京100041)

摘要：针对航空反潜声呐浮标布阵精度问题，提出一种减小浮标布阵误差的航线实验和分析方法。根据浮标布阵精度需求，设计浮标方形阵投放航线；进行飞行实验，分析浮标投放误差；分析风对浮标投放误差的影响。实验表明，通过合理的航线设计及误差控制，可改善浮标阵型的布阵误差。

关键词：航空反潜；浮标阵型；投放航线；投放误差

0引言

空投浮标布阵反潜是航空反潜的重要手段[1]，控制浮标投放精度是提升浮标阵反潜效率的有效措施，规划浮标投放航线是实现浮标高精度布阵投放的关键。规划浮标布阵航线目的是选择满足浮标布阵性能指标要求且满足飞机飞行性能的合理航线[2]。目前国内该领域主要开展了提高浮标阵搜索概率的声纳浮标布放阵型仿真研究[3-6]，关于浮标投放误差对阵型搜潜效能影响的研究未见报道。而在实际工程应用中，我们发现浮标投放误差对浮标阵效能发挥的影响是不可忽视的。投放误差过大可能导致阵型搜潜效能下降，甚至会使阵型中出现大的间隙而造成漏警。本文从工程实践角度提出一种减小浮标布阵误差的航线实验与误差分析方法，可以实现有效控制浮标布阵误差的目的。

1浮标阵型最大投放误差需求

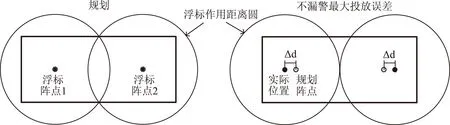
图1　浮标阵型不漏警最大投放误差示意

在规划浮标搜潜阵型时，通常要使两浮标作用区域有一定的重叠。浮标布阵允许的最大误差应满足浮标阵不漏警覆盖条件，即阵型内两枚浮标间不应产生覆盖空白，导致潜艇可能穿过浮标之间的空白而不被探测到。如图1所示。图1中，Δd为两浮标作用距离圆相切时，浮标实际位置与规划阵点位置之间的偏离距离。为避免出现漏警情况，将两浮标作用距离圆正好相切时的误差Δd定义为最大投放误差。

假设浮标作用距离为3 km，规划的浮标间距为4.8 km，由几何关系可知，浮标阵不漏警最大投放误差为600 m。在随机投放过程中，以正态分布模型描述误差分布，则要求±3σ范围为(-600 m,600 m)，即误差分布标准差要求3σ<600 m、 1σ<200 m。以此为例进行分析实验。

2航线实验与误差分析

浮标阵投放误差来源，一是采用自动导航飞行时产生的偏离航线误差，由偏航距描述，可称为横向误差(以航线方向为纵向)；二是浮标前飞投放时产生的偏离目标点误差，由投放射表描述，可称为纵向误差；三是风速风向的影响。

2.1横向误差

为分析横向误差，对方形浮标阵，针对某型直升飞机，设计两种飞行航线,如图2所示。

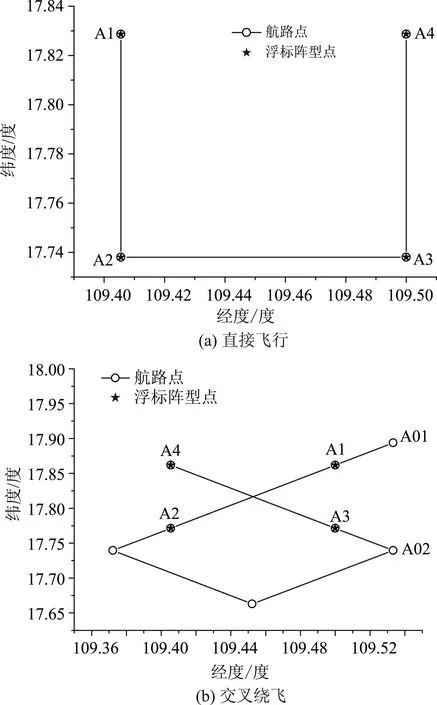
图2　方形阵飞行航线

直接飞行的轨迹如图3所示。

图3　直接飞行轨迹

用偏航距描述横向误差，偏航距分布如图4所示。

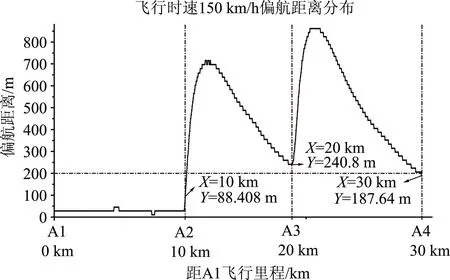
图4　直接飞行偏航距分布

由图4，在方形阵转弯点(A2、A3)，偏航距先迅速变大再逐渐收敛。对时速150 km/h，A2转弯点后飞行10 km，偏航距收敛至241 m；A3转弯点后飞行10 km，偏航距收敛<200 m。A3偏航距超过阵型最大投放误差需求。

交叉绕飞的飞行轨迹如图5所示。

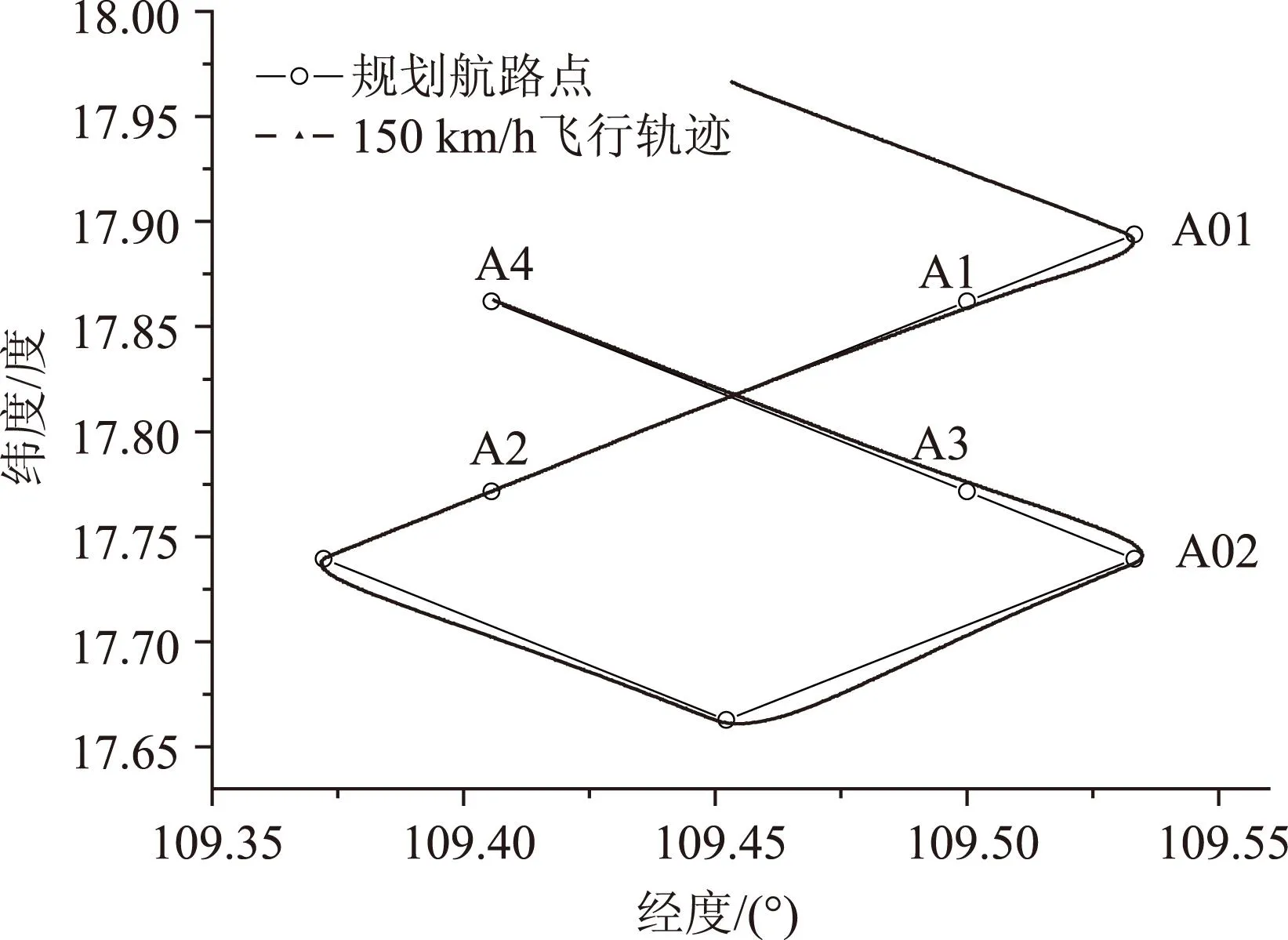
图5　交叉绕飞轨迹

偏航距分布如图6所示。

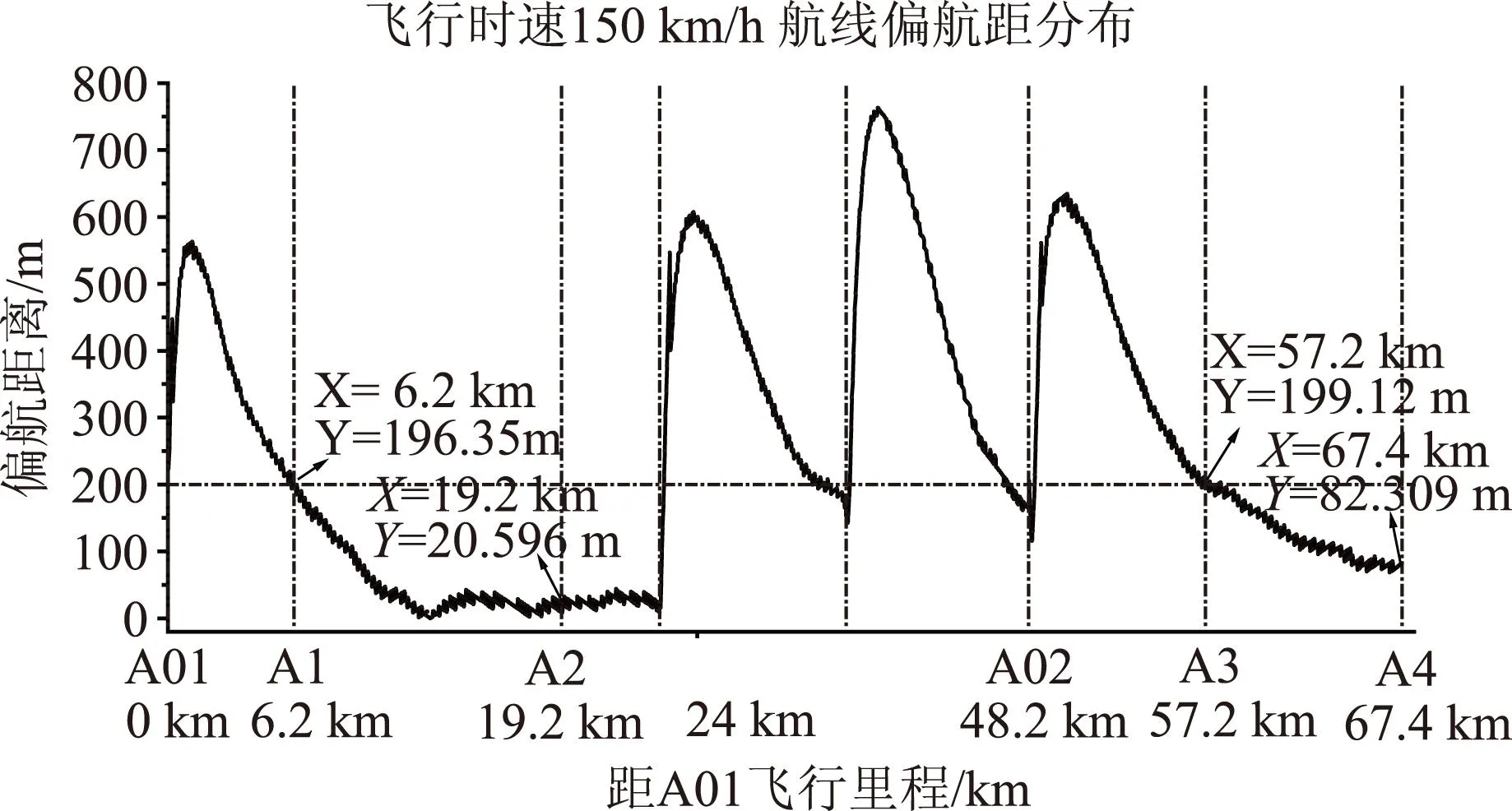
图6　交叉绕飞偏航距分布

由图6，通过增加导引点，使所有方形阵点(A1~A4)均在飞行直线。对飞行时速150 km/h，导引点A01与A1间距大于6.2 km、导引点A02与A3间距大于9 km时，可使阵点(A1-A4)偏航距均<200 m。

通过前述分析，为满足浮标阵型最大投放误差需求，设计投放航线时，可在阵型航线转弯点前增加航线导引点，导引点距离航线转弯点大于9 km。

2.2纵向误差

纵向误差是飞机沿航线方向前飞投放时，浮标实际入水点与规划阵点间偏离的距离，可通过计算浮标投放射表，按射表进行投放来控制纵向误差。

不考虑风影响时，浮标离机后，在垂直方向上自由落体、开伞入水；在水平方向上进行匀速运动、开伞减速。各时间段如图7所示。

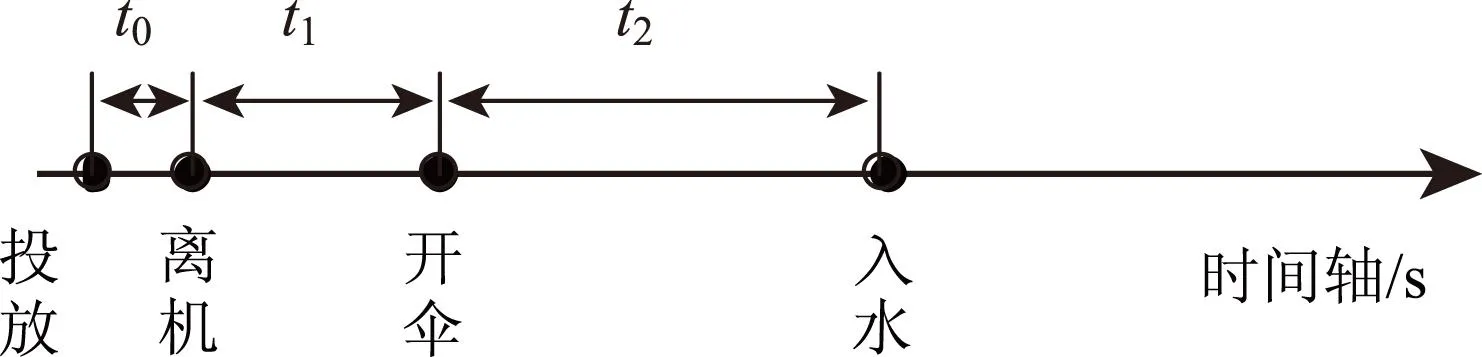
图7　浮标投放时间段示意

图7中，t0为投放按钮按下至浮标离机时间，即响应滞后时间；t1为浮标离机至浮标开伞时间；t2为浮标开伞后至浮标入水时间。

开伞后至入水浮标的运动模型如下：

浮标出舱后约1 s降落伞打开，在不考虑风速影响下，浮标运动受重力G和阻力Fs共同作用，如图8所示。

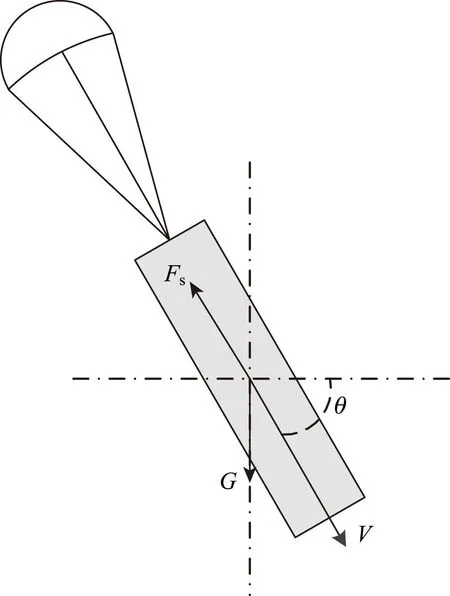
图8　浮标空中运动示意

图8中，Fs为降落伞阻力，G为重力，θ为速度方向与水平方向之间的夹角。开伞后浮标空中运动用以下方程组表示[7]：

(1)

式中,v为浮标空中运动速度;g为重力加速度;Cd为降落伞阻力系数;S为伞阻力面积;ρ为空气密度，一般为1.225 kg/m3;m为浮标质量。

纵向位移L及高度H与时间T的关系为：

(2)

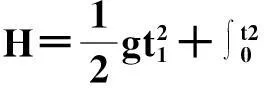
(3)

(4)

式中,v载机为载机飞行速度;t1为开伞时间;g为重力加速度;t2为浮标开伞后入水时间;v、θ由公式(1)确定，T为浮标入水时间。

由上述模型计算典型投放条件100 m投放高度、150 km/h投放速度下的浮标射表如表1。

表1　浮标投放射表

纵向误差σL主要来源是投放时刻载机位置误差σD、投放按钮响应滞后时间误差产生的位移st0、浮标出舱后开伞时间误差产生的位移st1、开伞后至浮标运动稳定状态产生的纵向位移误差ss，风的影响sw。

由各误差源可得到：

(5)

不考虑风的影响时，纵向误差为

(6)

假设各参数取值为：

载机位置误差为载机导航误差，设为σD=30 m；投放按钮响应滞后时间产生的位移误差为σt0=v载机Δt0,v载机为载机速度；Δt0为响应滞后时间误差，设为Δt0=0.5 s；浮标出舱后开伞时间产生的位移误差为σt1=v载机Δt1，v载机为载机速度；Δt1为出舱后开伞时间误差，设为Δt1=1 s；开伞后至浮标运动稳定状态产生的位移误差σs，设为σs=20 m。

在上述假设参数下，对典型投放条件(高度100 m和时速150 km/h)，浮标入水纵向误差为58.9 m。

在投放浮标时，根据浮标射表控制纵向偏移，可以实现对投放误差的控制。

2.3风的影响

实际投放时，除了浮标射表，还应考虑风的影响。

风的影响是风速风向对开伞后浮标运动状态产生影响，导致浮标投放位移偏差。浮标运动模型如下：

(7)

式中，v风为风速;φ为风向与载机航向间夹角(顺时针为正);L为离机浮标在航向纵向上的位移距离;θ为浮标速度方向与水平方向之间的夹角。

风的影响还导致浮标运动过程中在风向方向上发生整体偏移，偏移量为：

(8)

式中，L0，纵、L0，横为浮标在纵向和横向上发生的整体偏移。

假设载机在100 m高度，150 km/h速度的条件下投放，对5级风，风速在8 m/s~10.7 m/s范围，浮标投放纵向位移的变化情况如图9所示。

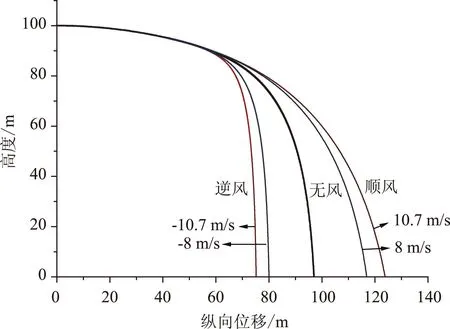
图9　风速起伏对纵向位移的影响(载机速度150 km/h)

由图9可见，5级风力(平均风速10 m/s)，投放高度100 m，载机速度150 km/h条件下，风速起伏带来的误差为5~7 m。

投放时，风的影响可通过计算风偏移量进行实时校正进行消除，但风速起伏造成的误差无法消除。

2.4总投放误差

通过前述分析，不同横向误差条件下，浮标投放误差如表2。

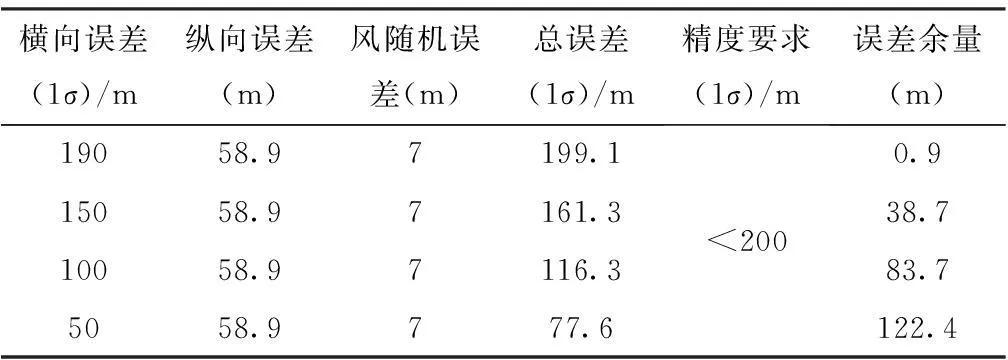
表2　浮标投放误差(载机速度150 km/h，投放高度100 m)

从表2可知，减小横向误差(偏航距小于190 m)，可使总误差满足浮标阵型最大投放误差需求，确保不漏警。对浮标方形阵投放航线，通过增加转弯导引点减小偏航距，控制横向误差，使总误差满足要求。

如进一步提升投放精度，还可采取按投放射表

提前或延后投放来控制纵向误差，或对风偏移量进行补偿修正等措施来减小总误差，提升精度。

3结语

本文从工程实践角度提出一种减小浮标布阵误差的航线实验与误差分析方法。依据浮标阵不产生漏警间隙条件确定最大投放误差需求；由最大投放误差需求设计投放航线进行实验，分析了横向误差、纵向误差及风的影响，形成浮标投放误差控制依据。提出利用导引点控制浮标布阵误差的方法，能够有效控制浮标阵型误差。

参考文献：

[1]康乐. 反潜直升机武器挂载方案研究与仿真[J]. 中国电子科学研究院学报， 2014，9(1)：70-74.

[2]陈芳，夏炜. 浮标布阵航路规划算法仿真研究[J]. 计算机仿真，2011,28(12):20-23.

[3]曾海燕，杨日杰，周旭. 声纳浮标搜潜优化布放技术研究[J]. 指挥控制与仿真， 2012， 34(1)：82-85.

[4]王磊，吴福初，陈钰宁. 基于声纳浮标的反潜直升机应召搜潜仿真研究[J]. 指挥控制与仿真， 2010，32(2):84-88.

[5]杨日杰，周旭，曾海燕. 被动全向声纳浮标跟踪潜艇的优化布放方法[J]. 指挥控制与仿真， 2011，33(5)：80-83.

[6]周旭，杨日杰，高学强，韩建辉. 基于遗传算法的被动浮标阵优化布放技术研究[J]. 电子与信息学报，2008,30(10)：2533-2536.

[7]张颜岭，赵洪，赵海潮. 声呐浮标空中运动曲线计算分析[J]. 声学与电子工程，2012,1：4-7.

蔡爱华(1962—)，男，江苏盐城人，中国电子科技集团公司首席专家，研究员级高工，主要研究方向为机载电子信息系统；

E-mail：caiaihua62@163.com

何建伟(1982—)，男，海南儋州人，工学博士，高级工程师，主要研究方向为机载电子信息系统总体技术；

王鹏(1990—)，男，陕西富平人，硕士，助理工程师，主要研究方向为机载电子信息系统总体技术。

Experiment and Error Analysis of Path Planning for Sonobuoy Array Deployment

CAI Ai-hua, HE Jian-wei, WANG peng

(Academy of Electronics and Information Technology, Beijing 100041, China)

Abstract:An Experiment and error analysis of path planning for sonobuoy array deployment was presented to improve the precision of sonobuoy array deployment for airborne anti-submarine. A deploying path of sonobuoy square array was designed according to the precision demand of array deployment. On the basis of flight experimental data, the deploying error was analyzed, and then the optimal design was applied by adding the introductory way point. Influence of wind during the deployment was also analyzed theoretically. The experiment results indicated that with the rational design and error control, the precision of sonobuoy array deployment could improve.

Key words:airborne anti-submarine; sonobuoy array; deploying path; deploying error

作者简介

中图分类号：TP202.2

文献标识码：A

文章编号：1673-5692(2016)01-021-05

基金项目：国家重大工程项目

收稿日期：2015-12-10

修订日期：2016-01-10

doi:10.3969/j.issn.1673-5692.2016.01.004