基于时频差测量的双机无源定位的线性解析方法

郁　涛

(中国电子科技集团第五十一所，上海　201802)

郁　涛(1957—)，男，上海人，高级工程师，主要研究领域为无源定位；

E-mail:18001648180@163.com



工程与应用

基于时频差测量的双机无源定位的线性解析方法

郁涛

(中国电子科技集团第五十一所，上海201802)

摘要：先将多普勒频移方程中的三角函数同时用直角坐标系和极坐标系的变量表示，然后通过联解对应于双机位置处的两个多普勒频移方程，消去多普勒频移方程中所包含的直角坐标系分量，可得到一个仅包含未知径向距离的方程。在此基础上，利用基于极坐标系的时差方程，即可直接解得目标的距离。更进一步，利用多普勒频移与时差之间的关系可消去方程中所包含的多普勒频移。由此得到仅基于时差和频差测量的无模糊测距解析解。

关键词：多普勒定位；时差；频差；测距；机载无源定位

0引言

利用双平台测量目标的TDOA-FDOA信息，理论上进行单次测量即可实现对目标的二维定位，现有的关于时差和频差的组合定位算法是在单一的直角坐标系中进行分析的，由此将涉及高阶非线性方程，不仅得不到显式解[1-3]，而且在求解中还会出现多值即模糊的现象，无法实现单次实时定位[4]。本文的分析表明，如直接在极坐标系中对时差和多普勒频移方程进行分析求解，且利用时差与多普勒频移间的关系，就能得到与多普勒频移无关的、仅基于时差和频差测量的单值解析解。

1频移的时差检测

如图1所示，设双机A和B同向同速沿x轴直线移动，且限定双机之间距离的量级，则根据几何关系，近似有时差测向公式：

(1)

由此可得到基于角度测量的近似时差检测公式：

(2)

式中：Δt为时差；θ目标的到达角；vc为光速；d为短基线的长度。

进一步设目标为固定或低速运动，通过利用多普勒频移：

λfd=vsinθ

(3)

即可得到时差与频移间的关系：

(4)

式中：λ为信号波长；fd是多普勒频移；v为探测平台的飞行速度。

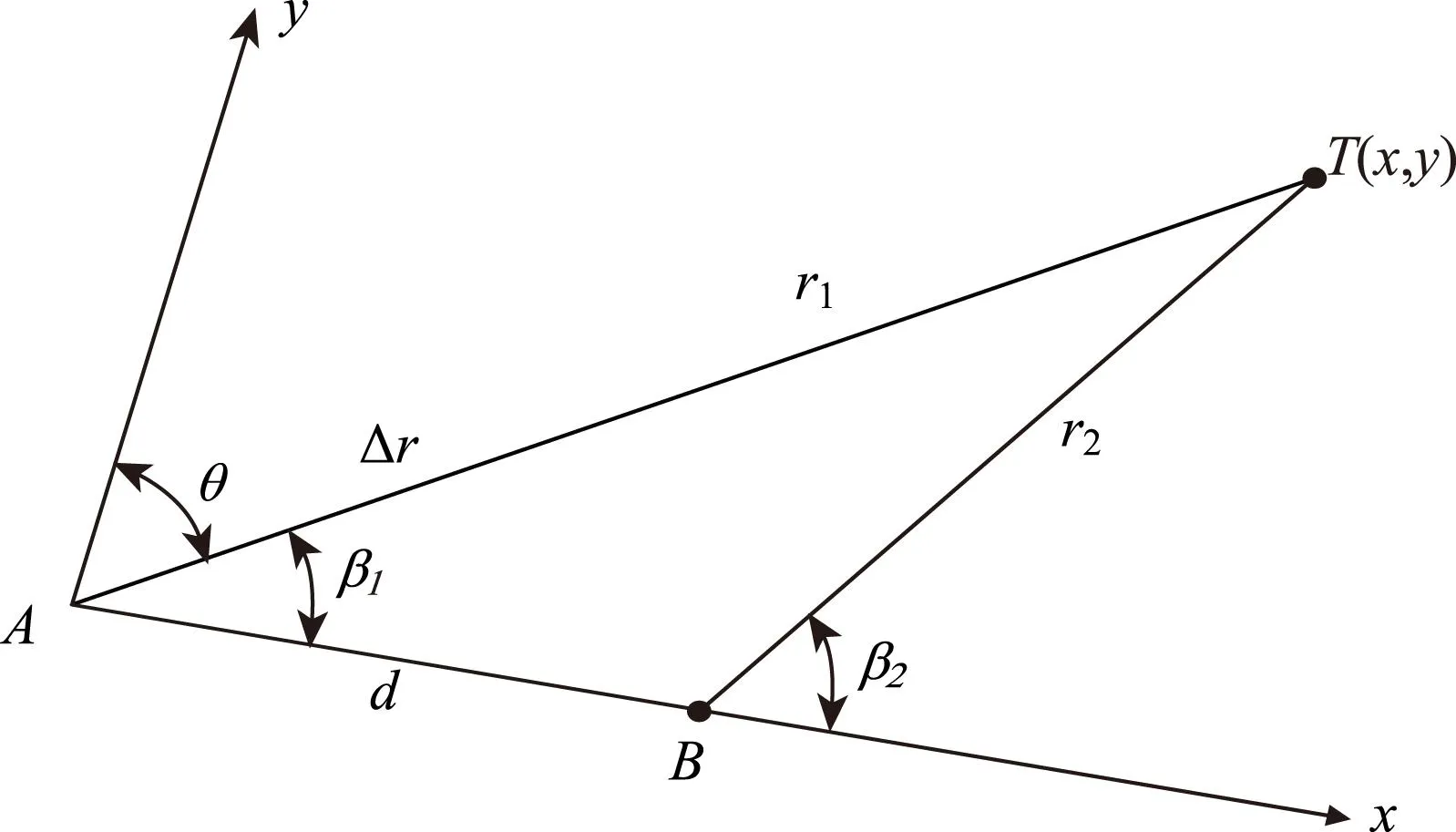
图1　基于时频差的双机无源定位

2线性测距解

2.1对频移方程的变量变换

根据图1所示的几何关系，由三角函数的定义，将多普勒频移方程中的三角函数同时用直角坐标系和极坐标系的变量来表示，对应于两次测量的频移值可列出如下方程：

(5)

(6)

式中：x为直角坐标系中的横坐标；ri为极坐标系中的径向距离；d为机载平台的移动距离。

移项整理后有：

(7)

(8)

两式相减，消去未知的直角横坐标分量后可得到仅和未知径向距离相关的方程：

(9)

2.2与频移无关的测距式

一旦将时差方程：

r1-r2=vcΔt

(10)

代入频移-距离方程(9)，可直接解出在机载平台B处的径向距离：

(11)

式中：Δfd=fd1-fd2为多普勒频差，可以用实测的信号频率的差值取代。

如将频移与时差之间的关系式(4)代入，即可得到与多普勒频移无关、仅基于时差和频差测量的无源测距式：

(12)

2.3相对计算误差

图2给出了在不同基线长度时，相对测距计算误差随目标到达角的变化曲线，且目标到达角是以机载平台B位置处为基准的。由于在推导过程中利用了近似时差测向方法，所以测距计算准确度有所降低，模拟计算表明，相对测距计算误差和基线长度成正比，对300 km远的目标，在基线长度小于30 km 时，相对计算误差可小于5%。

图2　不同站距时的相对测距计算误差

3误差分析

用全微分方法分析由频移、时差、速度以及平台运动距离的测量误差所产生的相对测距误差，当各观察量的误差都是零均值，相互独立而标准差分别为σΔf、σΔt、σv和σd时，相对测距误差公式为：

(13)

式中：σΔf、σΔt、σv和σd分别为频差、时差、速度和基线距离的测量误差均方根值。

径向距离对各个变量的偏微分是：

(14)

(15)

(16)

(17)

图3给出了在不同测频均方根值时的相对测距误差。模拟计算表明，频差测量误差是相对测距误差的主要因素，且仅在频差测量误差小于100 Hz时，才能实现小于5%R的技术要求。

模拟计算式所用的各个变量的测量误差的均方根值为：σΔt=100 ns，σv=0.1 m/s，σd=20 m，其余的参量有：r1=300 km，v=100 m/s，d=3 km，λ=0.03 m。

图4计算结果说明增大两探测平台之间的距离能降低测距误差，计算所用的频差测量误差均方根值为1000 Hz。

图3　不同频差测量误差时的相对测距误差

图4　不同站距时的相对测距误差

4结语

本文的分析表明，如对多普勒频移方程采用变量变换，恰当的消除直角坐标系的变量，则就能在极坐标系中直接获得目标距离的无模糊解析解。且误差分析表明，只要频差测量的误差能控制在100 Hz之内，则在基线长度较短的情况就能满足5%R的技术要求。如频差测量精度较低，则可通过加大两探测平台之间的距离来提升对目标的测距精度。

参考文献：

[1]陆安南. 双机TDOA/DD无源定位方法[J]. 电子科技大学学报, 2006,35(1):17-20.

[2]冯天军. 双机时差-频差组合定位研究[D]. 长沙：国防科学技术大学研究生院，2008:18-44.

[3]侯燕. 无源时差频差定位方法的研究[D].南京：南京理工大学, 2007:39-44.

[4]崔弘珂,王玉林. 三机时差频差联合定位精度分析[J].无线电工程, 2011,41(7): 21-23.

郁涛(1957—)，男，上海人，高级工程师，主要研究领域为无源定位；

E-mail:18001648180@163.com

Linear Analytic Method for Double-plane Passive LocationBased on TDOA and FDOA

YU Tao

(The 51th Research Institute of CETC, Shanghai 201802 China )

Abstract:If the circular function in Doppler shift equation can be expressed concurrently as the variable in rectangular coordinate system and polar coordinate system, an equation only containing unknown radial distance can be obtained by expunging the variable in rectangular coordinate system making use of simultaneous inference for two Doppler shift equations corresponding to the location of two airplanes. On this basis, the object distance can be derived by using time difference equation based on polar coordinate system. What’s more, by expunging the Doppler shift in equation making use of the relationship between Doppler shift and time difference, we can obtain an unambiguous analytic solution of passive ranging which is only associated with time difference and frequency difference.

Key words:Doppler location; time difference; frequency difference; ranging; airborne passive location

作者简介

中图分类号：TN953

文献标识码：A

文章编号：1673-5692(2016)01-029-03

收稿日期：2015-10-29

修订日期：2015-12-29

doi:10.3969/j.issn.1673-5692.2016.01.006