基于EMD和SVD的在线手写签名特征提取方法

李成华，龚良慧，江小平，孙　婧

(中南民族大学 电子信息工程学院，武汉 430074)



基于EMD和SVD的在线手写签名特征提取方法

李成华，龚良慧*，江小平，孙婧

(中南民族大学 电子信息工程学院，武汉 430074)

摘要为使在线手写签名认证的使用更具实用性，提出了一种基于经验模态分解(EMD)和奇异值分解(SVD)的在线手写签名特征提取方法.针对在线签名数据的坐标信息，以EMD分解所得的本征模态函数(IMF)分量为初始矩阵，并进行矩阵奇异值分解，以奇异值的能量值作为样本数据的特征分量构成用户特征向量，建立了基于支持向量数据描述(SVDD)的一类认证模型验证该方法效果.在SVC2004签名数据库上的实验结果表明：该方法提取的签名特征区分明显，使用少量的单类真实签名作为训练样本，得到FAR=3.38%，取得了较好的认证识别效果.

关键词在线手写签名；特征提取方法；经验模态分解；奇异值分解

Feature Extraction Method for On-Line Handwriting Signature Based on EMD and SVD

LiChenghua,GongLianghui,JiangXiaoping,SunJing

(College of Electronics and Information Engineering, South-central University for Nationalities, Wuhan 430074, China)

AbstractIn order to make the use of on-line handwriting signature verification more practical, this paper presents a feature extraction method based on Empirical Mode Decomposition (EMD) and Singular Value Decomposition (SVD). With the help of signatures′ coordinate information, the initial feature matrix of Intrinsic Mode Function (IMF) components decomposed by EMD is SVD transformed, and use the energy value of the first two singular values as the characteristic component of the signature data, then the certification model of one-class identification is established based on Support Vector Data Description (SVDD) with a small amount of real signature to validate the effect. Experimental results from the SVC2004 signature database show that the characteristics extracted by this method distinguished clearly, and use a small number of one class real signatures as training samples, achieved a better recognition result with FAR=3.38%.

Keywordson-line handwriting signature; feature extraction method; empirical mode decomposition (EMD); singular value decomposition (SVD)

每个人在签名时的运笔压力、运笔速度、行笔顺序等方面都具备各自的特点，承载着表征签名者身份的固有特征[1]，虽然伪造者可以模仿字形，但是这些动态特征是模仿者难以伪造的.目前，基于动态特征的在线签名特征提取方法大多针对签名设备采集的坐标信息、力信息、旋转角度、接触面积等一系列动态信息进行特征提取[2-6].例如，文献[2]针对手写触摸屏设备获得的签名数据，提取签名信息中的压力信息作为签名特征.但是考虑到目前绝大多数的移动计算设备易于采集触点的坐标信息，对于触屏压力、接触面积等信息却并非都能准确获得，因此选择针对签名触点的坐标信息开展特征提取研究更为实际.

此外，有关利用小波变换方法进行在线手写签名特征提取的报道较多，例如，文献[3]和[4]提出利用小波包分解和单支重构来构造能量特征向量的方法, 直接利用各频段成分能量的变化来反映签名的动态特征.小波变换在一定程度上弥补了傅里叶变换的缺陷[7]，但归根到底还是以傅里叶变换为基础的，小波基选择困难，小波基一经选定就无法改变，不具有自适应性.经验模态分解(EMD)的出现，提供了一种较好的自适应分解方法.它既具有小波变换多分辨的优势，又克服了小波变换使用中小波基选取的难题[8-10].目前EMD已经在许多领域得到应用，例如，文献[11]提出了一种在EGG 中识别梭形波的新方法，通过对EEG信号作EMD自适应分解，并根据Hilbert谱自动识别梭形波；文献[12]使用基于EMD和SVD的方法提取虹膜特征，提取的特征向量维数少，识别率高，具有较好的应用价值.因此，本文尝试将EMD引入到在线签名的特征提取方面.

在认证过程，大多数的签名认证方法都把其作为二类分类来处理，同时在注册阶段使用的训练样本数过多，例如，文献[4]取10个真实签名和10个伪造签名进行训练.但是，根据签名样本分布的特点(注册阶段，真实签名样本少，而且伪造签名样本难以获取)来看，认为把在线签名认证看作一类分类问题来处理更为合理恰当[13]，而且为提高实用性应当使用尽可能少的真实样本作为训练样本.

基于以上考虑，为使在线手写签名认证的使用更具实用性，本文设计了一种基于经验模态分解和奇异值分解(SVD)的在线手写签名特征提取自适应方法，使用签名触点的坐标信息，以EMD分解所得的本征模态函数(IMF)分量为初始矩阵，并进行SVD分解，以奇异值的能量值作为样本数据的特征分量构成用户特征向量.鉴于支持向量数据描述(SVDD)在小样本、一类分类问题上的优越性，通过建立基于SVDD的一类认证模型验证本文方法效果.

1经验模态分解

1998年N.E. Huang等人提出了一种新的信号处理方法——经验模态分解.该方法从本质上讲是对一个信号进行平稳化处理，其结果是将信号中存在的不同尺度下的波动或趋势逐级分解开来，产生一系列具有不同特征尺度的数据序列，每个序列称为一个IMF.IMF必须满足以下两个条件.

(1) 信号的极值点(极大值或极小值)数目和过零点数目相等或最多相差一个；

(2) 由局部极大值构成的上包络线和由局部极小值构成的下包络线的平均值为零，即信号关于时间轴局部对称.

对任一给定的信号X(t)的EMD过程如下.

(1) 首先确定X(t)的所有极值点，用三次样条曲线连接所有极大值点形成上包络线eup(t)，同样的方法形成下包络线elow(t).计算上下包络线的均值m1(t) =[eup(t) + elow(t)] / 2.

(2) 将X(t)与m1(t)的差记为h1(t)，即h1(t) = X(t) - m1(t)，若h1(t)不满足IMF条件，则将其视为新的X(t)，重复上述步骤k次，直到hk(t) = hk-1(t)- mk(t)满足“筛选停止准则”，即：

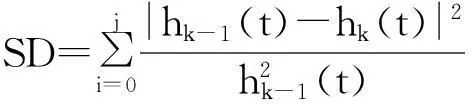
(1)

其中，hk(t)和hk-1(t)是在筛选IMF分量的过程中两个连续的处理结果，l是分解信号的长度，SD的值一般在0.2到0.3之间.这样就得到从原始信号分离出的第一个IMF分量C1(t)，记C1(t) = hk(t).

(3) 可得到剩余分量r1(t) = X(t) - C1(t)，由于r1(t)仍然包含周期的分量信息，仍可作为“新”信号.重复上述过程，依次分解得到C2(t)，C3(t)，…，Cn(t)，直到rn(t)成为单调函数或常数，不能再筛分出IMF分量，则停止EMD分解，此时残余信号rn(t) = rn-1(t) - Cn(t)，即有：

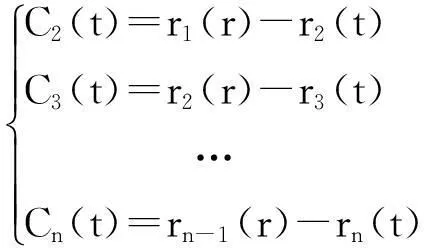
(2)

(4)至此，信号X(t)可表示为n个IMF分量和一个残余项之和的形式，即

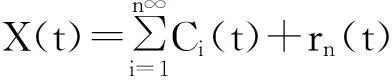
(3)

式中，rn(t)为残余项，代表信号中的平均趋势；Ci(t)为依次分解得到各个IMF分量，分别代表信号从高到低不同频率段的成分.

2基于EMD和SVD的特征提取方法

2.1签名数据预处理

本文使用签名数据的触点坐标信息，并针对其所形成的速度时间序列和加速度时间序列提取签名特征.首先，对原始触点坐标数据进行预处理工作，包括去除签名数据中的重采样点、错误时间间隔点(时间间隔为负数或间隔明显过于相近)以及归一化处理.然后，通过计算可以得到坐标的多种速度时间序列和加速度时间序列，本文选择速度时间序列(v,t)、速度在横轴方向的时间序列(vx,t)、速度在纵轴方向的时间序列(vy,t)、加速度时间序列(a,t)、加速度在横轴方向的时间序列(ax,t)、加速度在纵轴方向的时间序列(ay,t)等共6个时间序列数据进行时频域特征提取.

2.2基于EMD和SVD的特征提取方法

按前述方法，对上述6个时间序列进行EMD自适应分解，获得多个IMF数据，(对不同时间序列和不同用户数据，分解得到的IMF数目并不完全一致，一般为5～7个).IMF数据量大，不宜直接表征用户特征.矩阵的奇异值在反映矩阵的固有特征上具有良好的稳健性.本文对所得的IMF分量构成的初始特征矩阵进行SVD分解，获得一维的奇异值向量，向量的数据长度与其EMD分解所得的IMF分量的个数相同.奇异值反映了有用信号和噪声的能量集中情况，前几个较大的奇异值主要反映有用信号，而较小的奇异值主要反映噪声[14]，本文仅使用前两个奇异值.对比了方差、平均值、能量值的实验效果之后，发现前两个奇异值的能量值作为签名数据的特征量更能稳定表征用户的个性特征.

本文方法的示意图如图1所示，其主要步骤描述如下.

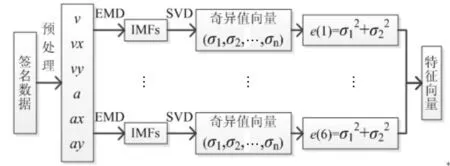
图1　基于EMD和SVD的特征提取方法示意图Fig.1　Molecular structure of feature extraction methodbased on SVD and EMD

(1) 对签名过程中形成的触点坐标数据进行预处理后，计算得到3个速度时间序列(v, t)、(vx, t)、(vy, t)，以及3个加速度时间序列(a, t)、(ax, t)、(ay, t).

(2) 对每个时间序列分别进行EMD自适应分解，得到若干个IMF分量以及一个残余项，不同信号的IMF个数不一定一致.

(3) 对一个时间序列所得到的IMF分量以及残余项所组成的特征矩阵进行SVD分解，得到一维的奇异值向量(σ1, σ2, ……, σn).为消除各分量因大小范围不一对SVD的影响，分解前先进行归一化处理，并将幅值限定在0 ～ 1范围内.

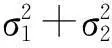
(5) 得到用户特征向量：一个签名样本对应的速度时间序列以及加速度时间序列共6个时间序列，每个时间序列按上述步骤(2)～(4)获得一个特征分量，6个特征分量构成表征用户签名数据的特征向量T = [e(1), e(2), e(3), e(4), e(5), e(6)].

3实验

数据来源：本文以SVC2004国际签名认证大赛所提供的数据作为签名数据库.该签名数据库提供中文签名和英文签名，每个签名文件以文本形式存储，表示为一系列的采样点，记录签名在采样点的坐标信息、时间值等签名信息.每个用户的签名数据包含20个真正的签名样本和20个熟练伪造的签名样本.

签名者在签名时承载着表征签名者身份的固有特征，如图2所示是两个真实签名样本和两个伪造签名样本的坐标信息的vx速度曲线对比图.同一个签名者的书写习惯具有一定的稳定性，而伪造者的签名在速度时间序列上具有比较明显的区分度，它们的极值点出现的时刻和峰值大小与真实样本比较起来都有明显的差异.

以签名数据库中编号为U37用户签名数据的vx速度时间序列为例，采用EMD方法对vx进行分解，得到一系列的IMF分量以及一个残余项.通过一系列的实验，发现一个签名数据一般分解得到5～7个IMF分量，对于同一个签名者的真实签名样本，其EMD分解的IMF曲线具有类似的变化趋势，而伪造者提供的伪造签名的EMD分解结果往往表现为不一样的变化趋势，如图3所示.因此，IMF分量和残余项可以用来反映用户签名的特征.

分解所得的IMF数据量较大，不宜直接用来建立用户认证模型，本文将签名时间序列数据进行EMD分解后所得的IMF分量组成初始特征矩阵，对其进行SVD分解，用奇异值向量的相关信息量作为用户特征向量的分量.表1所示是对用户U37多次签名的vx数据对应的初始特征矩阵进行SVD分解所得到的奇异值，其中“—”表示无数据，签名S18～S20是用户U37的真实签名，S21～S23为其伪造签名.可以看出，SVD分解后得到的奇异值向量能够很好地区分真实样本和伪造样本，特别是二者的前两个值区分度尤为明显.经过试验对比，取奇异值向量的前两个值并以其能量值作为一个特征分量.

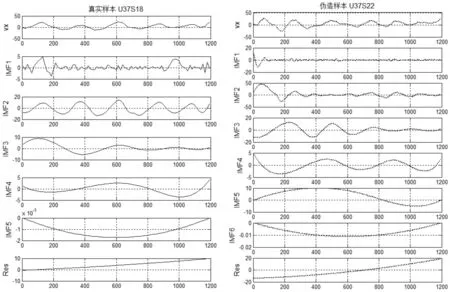
图3　真伪样本vx速度的EMD分解对比结果Fig.3　Comparison char of the EMD results with vx speed of real signatures and forged signatures

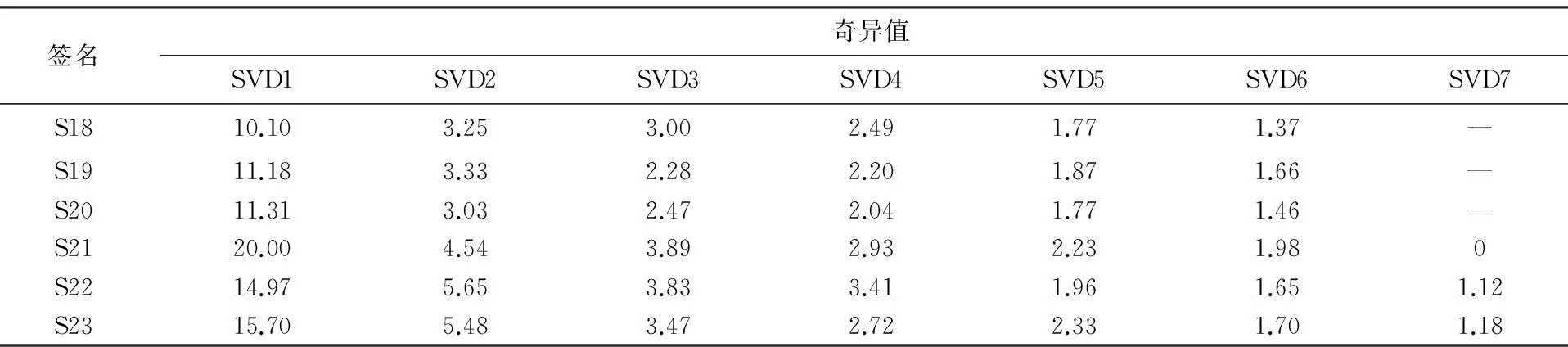
签名奇异值SVD1SVD2SVD3SVD4SVD5SVD6SVD7S1810.103.253.002.491.771.37—S1911.183.332.282.201.871.66—S2011.313.032.472.041.771.46—S2120.004.543.892.932.231.980S2214.975.653.833.411.961.651.12S2315.705.483.472.722.331.701.18

同样，一个签名样本对应的其余时间序列做相同的特征提取，对6个时间序列分别处理获得6个特征分量，构成表征用户签名数据的特征向量.对用户U37的所有签名样本进行特征提取所获得的特征向量曲线如图4所示，并结合如图5所示的用户真伪签名样本的特征平均值曲线，可以看出，真实样本所提取的特征向量数值较小，分布情况比较稳定.但是伪造样本所提取的特征向量数值较大，而且分散.与真实样本的特征向量相比，层次差别明显，很好的将真伪样本的特征区分开来，达到了特征提取的目的.

为了进一步验证本文方法的特征提取效果，我们设计了认证模型进行验证.本文在签名认证阶段引入了SVDD方法，并以一类分类问题为出发点，以少量的真实签名作为训练样本，建立认证模型.在此过程中，实验所选用的训练样本数与平均准确率的相关性曲线如图6所示.基于使用尽可能少的真实样本作为训练样本的原则，对SVC2004签名数据库的每个签名用户取6个真实签名作为训练样本(注册阶段不使用伪造样本)，以20个真实签名和20个伪造签名作为待测签名用来测试.其中SVDD的核函数选择径向基核函数(RBF)，参数设置为c=1，g=0.000001.在测试阶段，以认假率(FAR)、拒真率(FRR)以及准确率(ACC)进行结果统计，得到的实验结果如图7所示，其FRR平均值为3.38%，FAR平均值为10.25%，ACC平均值为86.63%.

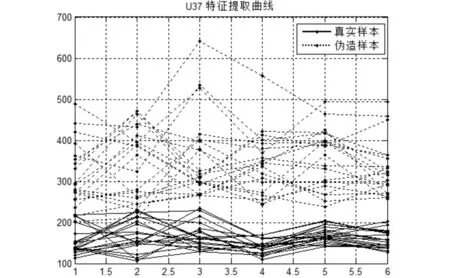
图4　U37签名样本的特征提取结果Fig.4　The feature extraction results of signature sample U37

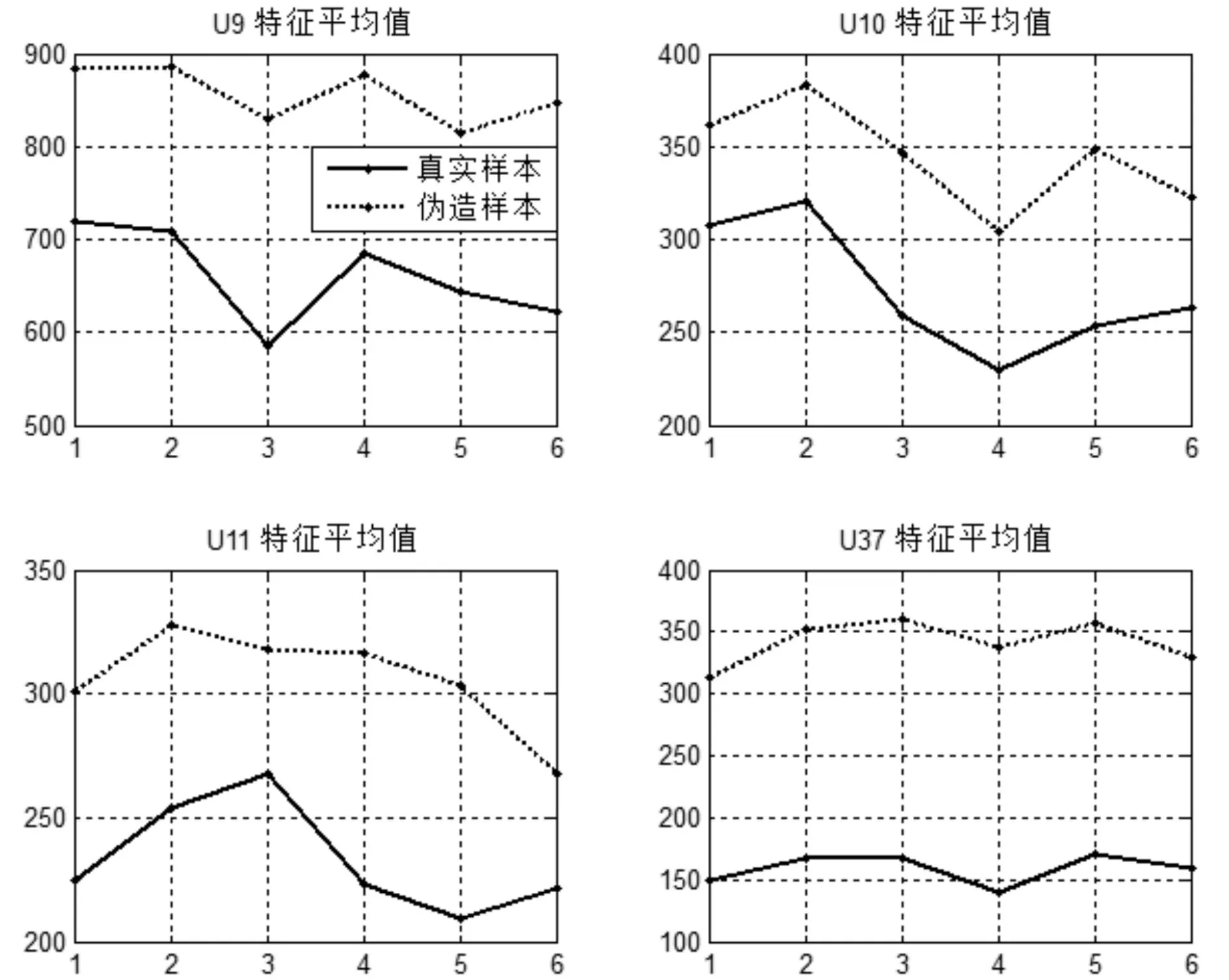
图5　用户真伪签名样本的特征平均值曲线 Fig.5　Average value of the feature extraction results of users′signature samples

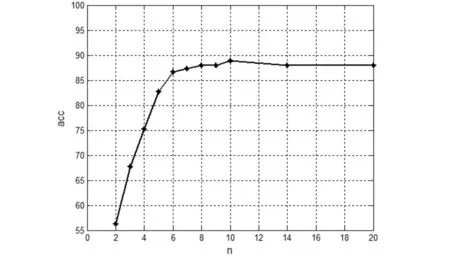
图6　训练样本数与平均准确率的相关曲线 Fig.6　The correlation between the number of training samples and the average accuracy

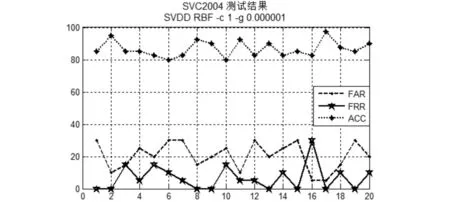
图7　在线签名的认证结果Fig.7　Certification results of online signatures

将实验结果与文献[2]和文献[4]作对比，如表2所示.与之相比，本文方法取得了较好或较为接近的认证效果，但本文使用常用设备易于采集的坐标数据，而非压力、旋转角度等信息，在训练阶段使用的训练样本数更少，且仅使用真实签名作为训练样本，更能真实地反映实际应用场景.

表2　不同特征提取方法的对比结果

4结语

本文针对在线签名数据坐标信息的速度时间序列和加速度时间序列，采用基于EMD和SVD的自适应方法提取签名特征，并以SVDD方法进行签名认证.实验结果表明：该方法提取的签名特征区分明显，仅使用少量的单类真实签名作为训练样本，依然能够得到较小的FAR值，取得了较好的认证识别效果，具有较高的实用价值.在进一步的研究中，我们将考虑如何优化EMD方法，在保证运算速率的前提下，克服端点效应、频率混叠等问题，取得更稳定且区分度更高的签名特征，并对SVDD的核函数以及核函数参数做出优化选择，进一步提高认证性能.

参考文献

[1]尤庆成. 基于HMM_SVM混合模型的在线手写签名认证[D]. 合肥：中国科学技术大学, 2010: 21-26.

[2]颜 琬. 基于小波分析和DTW的在线手写签名验证方法研究[D]. 武汉：武汉理工大学, 2005: 18-22.

[3]马海豹, 刘漫丹, 张 岑. 基于小波包分析的在线手写签名认证方法[J]. 计算机工程与应用, 2007, 43(12): 235-238.

[4]马海豹, 刘漫丹, 张 岑. 基于小波包分析和SVM的在线手写签名鉴别[J]. 华东理工大学学报(自然科学版), 2007, 33(4): 541-545.

[5]Zhang L P, Wu Z C. On-line signature verification based on wavelet transform to extract characteristic points[M]. Berlin: Springer, 2006: 1002-1007.

[6]Mondal T, Bhattacharya U, K S, et al. On-line hand-

writing recognition of Indian scripts - the first benchmark[M]. NJ: IEEE, 2010: 200-205.

[7]Bolesa W W. A security system based on human iris identification using wavelet transform[J]. Engineering Applications of Artificial Intelligence, 1998, 2(1): 533-541.

[8]Chang C P, Lee J C, Su Y, et al. Using empirical mode decomposition for iris recognition[J]. Computer Standards & Interfaces, 2009, 31(4): 729-739.

[9]Xuan B, Xie Q, Peng S. EMD sifting based on bandwidth[J]. Signal Processing Letters IEEE, 2007, 14(8): 537-540.

[10]Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceeding of the Royal Society, 1998, 454: 903-995.

[11]杨志华, 齐东旭. 一种基于EMD的睡眠脑电图梭形波自动识别方法[J]. 北方工业大学学报, 2005, 17(1): 1-4.

[12]罗忠亮, 林土胜, 杨 军, 等. 基于EMD和SVD的虹膜特征提取及识别[J]. 华南理工大学学报(自然科学版), 2011, 39(2): 65-69.

[13]刘 东. 基于支持向量数据描述的在线签名认证研究[D]. 合肥：中国科学技术大学, 2012: 31-33.

[14]段向阳, 王永生, 苏永生. 基于奇异值分解的信号特征提取方法研究[J]. 振动与冲击, 2009, 28(11): 30-33.

中图分类号TP391

文献标识码A

文章编号1672-4321(2016)01-0103-05

基金项目湖北省自然科学基金项目(2014CFB916);中央高校基本科研业务费专项资金资助项目(CZW15043)

作者简介李成华(1972-)，男，副教授，博士，研究方向：云计算、信息安全，E-mail: tylch@163.com

收稿日期2015-10-10*通讯作者龚良慧(1990-)，男，硕士生，研究方向：身份认证技术，E-mail：glhkung@163.com