巧用概率方法证明不等式

贾朝勇，潘玉荣（蚌埠学院数理系，安徽蚌埠233030）



巧用概率方法证明不等式

贾朝勇，潘玉荣
（蚌埠学院数理系，安徽蚌埠233030）

摘要：通过实例展示了如何巧妙借助概率论的思想方法来证明不等式，其关键点是：根据待证不等式具体形式去构造适当概率模型，再应用随机事件的运算、概率的相关性质、随机变量函数的数学期望的定义、切比雪夫不等式或马尔克夫不等式等证明不等式。此种证明方法不仅为证明不等式提供了一种新思路，而且还沟通了不同数学学科之间的联系。

关键词：不等式；概率模型；随机变量；切比雪夫不等式；马尔克夫不等式

不论是在初等数学还是在高等数学中，不等式证明都是一个重要的知识点，也是难点。不等式的证明常见方法有比较法、分析法、放缩法、反证法和构造函数法（导数法）等，但对于一些特殊不等式的证明用这些方法可能很难证明出来，此时可借助其他数学学科的知识来证明，其中用概率方法证明不等式，是概率论的一个重要研究方向［1］。已有学者用概率方法证明一些关系式，例如，刘军、张晓梅等研究了用概率方法证明某些等式［2-3］；刘敬、汤茂林等研究了用概率论中数学期望或数学期望相关的不等式去证明不等式［4-5］。本文将利用两类概率方法证明不等式，其中第1类是根据不等式的特点构造合适的概率模型，利用随机事件的运算、概率的性质、随机变量的数学期望性质等证明不等式；第2类是根据不等式的特点利用概率论中的重要不等式：切比雪夫不等式、马尔克夫不等式去证明不等式。

1　构造概率模型证明不等式

1.1利用概率的性质证明不等式

性质1随机事件的概率总介于0和1之间。

例1已知0＜xi＜1，i=1，2，3，求证

分析：构造一个事件，使得不等式的左边恰好是某一随机事件的概率，再根据随机事件概率不超过1即可证明该不等式。

证明构造3个相互独立的事件，设A1、A2、A3是3个相互独立的随机事件，对应的概率分别为对立事件的概率分别为则

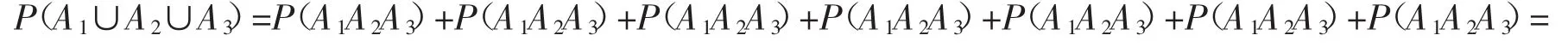
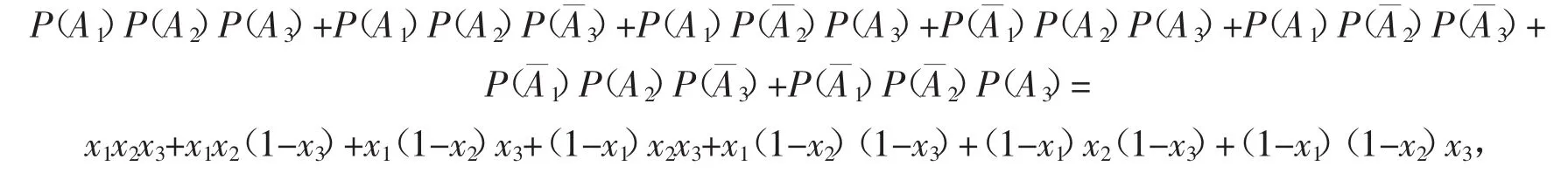
又因为P（A1∪A2∪A3）≤1，所以

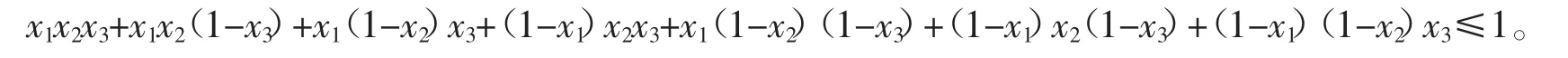
性质2任意两个随机事件A、B和的概率不大于事件A与事件B的概率之和，即P（A∪B）≤P（A） +P（B），更一般的结果是：A1，A2，…，An是n个随机事件，则有再注意事件的概率均为0到1之间的数，根据不等式的特点，通过构造合适的和事件证明不等式［6-7］。

证明构造这样一个摸球模型：现有4个袋子，第1个袋子有a个球，其中只有一个红球；第2个袋子有b个球，其中只有一个红球；第3个袋子有c个球，其中只有一个红球；第4个袋子有d个球，其中只有一个红球，考查至少摸到一个红球的概率。

设Ai表示从第i个袋子摸到红球，i=1，2，3，4，显然A1、A2、A3、A4相互独立且有由概率性质知，即

所以

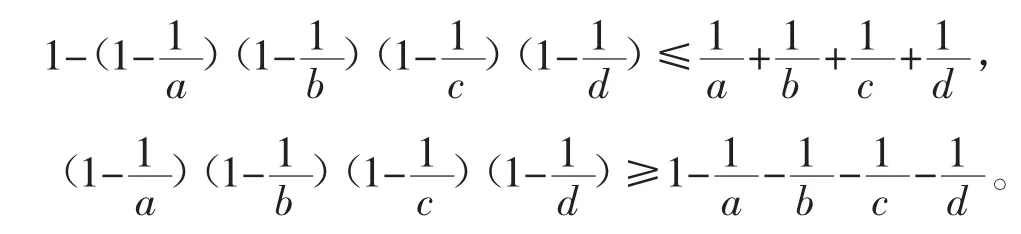
即

性质3若事件B是事件A的子事件，即A⊃B，则P（A）≥P（B）。

例3设0＜a、b、c、d＜1，求证（a+b-ab）（c+d-cd）≥ac+bd-abcd。

证明构造4个相互独立的事件A、B、C、D，对应的概率分别为P（A）=a，P（B）=b，P（C）=c，P（D）=d，显然（A∪B）（C∪D）⊃AC∪BD，所以P（（A∪B）（C∪D））≥P（AC∪BD），由于A、B、C、D是相互独立的事件，所以有

所以

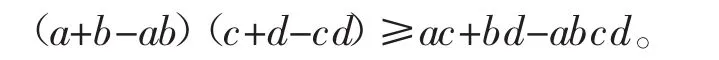
1.2利用离散型随机变量分布律的基本性质证明不等式

证明借助几何分布和n重贝努利试验的思想，构造一个无限次贝努利概率模型：将随机试验E进行无限次重复试验，每次随机试验E只有事件A发生和事件A不发生这两个结果，且第k次A发生的概率为记随机变量X表示事件A首次发生需要的试验次数，则X的分布律为

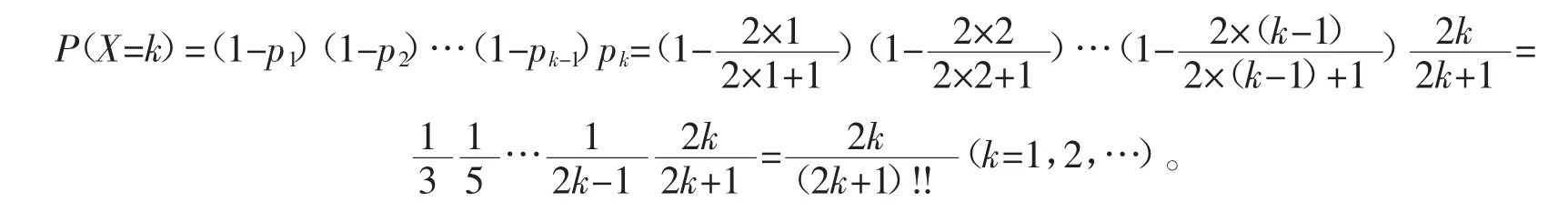
1.3利用数学期望、方差的定义或性质证明不等式

对于某些不等式的证明，可以借助随机变量函数的数学期望来证明。

由D（X）=E（X2）-（E（X））2，得E（X2）=D（X）+（E（X））2=6。

利用方差的非负性可以证明不等式：设离散型随机变量X的分布律为P（X=k）=pk，k=1，2，…，因此E（X）2≥（E（X））2；且等号成立的条件是x1=x2=…= E（X）。应用E（X）2≥（E（X））2的关键是构造一个分布律X，使得E（X）2恰好是待证不等式一边的式子或这个式子的倍数。

例6已知x+2y+3z+4u+5v=30，求证x2+2y2+3z2+4u2+5v2≥60。

证明构造随机变量X的分布律，如表1所示。

表1　随机变量X的分布律

又因为x+2y+3z+4u+5v=30，所以E（X）=2，因此5v2≥60；当且仅当x=y=z=u=v=E（X）=2时，等号成立。

2　利用概率论中的重要不等式证明不等式

2.1利用切比雪夫不等式证明不等式

定理1（切比雪夫不等式）设随机变量X的数学期望E（X）和方差D（X）都存在，则对任意正实数ε，有或

2.2利用马尔克夫不等式证明不等式

定理2（马尔克夫不等式）设X为非负随机变量，则对任意正实数a，有

证明根据待证不等式左边的形式特点，构造随机变量X服从参数λ=1的普松分布，即X～P（1），其分布律为其数学期望E（X）=1，对任意的正整数n，代入马尔克夫不等式得：，即不等式成立。

3　结语

本文通过列举实例展示了如何利用概率方法证明不等式，应用概率方法证明不等式的关键之处是：根据待证不等式的具体形式去构造适当概率模型，再应用概率论中的随机事件的运算、概率的相关性质、离散型随机变量分布律的基本性质、随机变量数学期望的有关计算或重要不等式等加以证明［8］。巧妙地利用概率方法证明某些不等式，证明思路清晰明了，证明过程简洁、高效，往往能起到事半功倍的效果，同时还沟通了不同数学学科之间的联系。

参考文献:

［1］王梓坤.概率论基础及其应用［M］. 3版.北京:北京师范大学出版社, 2013.

［2］刘军,望清凤.数学分析中一些等式的概率方法证明［J］.三峡大学学报:自然科学版, 2005, 27（3）: 283- 285.

［3］张晓梅,李红梅.概率论在高等数学中的应用研究［J］.赤峰学院学报:自然科学版, 2014, 30（6）: 4- 5.

［4］刘敬.数学期望不等式的应用［J］.河北北方学院学报:自然科学版, 2008, 24（4）: 6- 7.

［5］汤茂林.一个概率不等式的应用［J］.凯里学院学报, 2012, 30（3）: 160- 161.

［6］盛骤,谢式千,潘承毅.概率论与数理统计［M］. 4版.北京:高等教育出版社, 2008.

［7］张德然.概率论思维论［M］.合肥:中国科学技术大学出版社, 2006.

［8］杨春波,程汉波.利用概率分布巧证不等式［J］.数学通讯, 2013（7）: 27- 28.

【责任编辑：王桂珍foshanwgzh@163.com】

Proving inequalities by using probability method

JIAChao- yong, PANYu- rong
（Department of Mathematics and Physics, Bengbu University, Bengbu 233030, China）

Abstract:This paper shows howtouse the ideas and methods ofprobabilitytheorytoprove inequalitythrough the examples cited toreaders, the keypoint is accordingtothe specific formofinequalitytoconstruct the appropriate probability model, then using computation of random events, and the related properties of probability, the definition ofmathematical expectation ofrandom variable function, Chebyshev inequality or Markov inequality to prove inequality. The proof method provides a new idea for proving inequality, and also communicates the connection between different mathematics subjects.

Keywords:inequality; probabilitymodel; randomvariables; Chebyshevinequality; Markovinequality

作者简介：贾朝勇（1978－），男，安徽郎溪人，蚌埠学院讲师。

基金项目：安徽省高等学校优秀青年教师人才科研资助项目（2012SQRL215）；蚌埠学院教研项目（2013jyxm04）

收稿日期：2015-10-13

文章编号：1008- 0171（2016）02- 0012- 05

中图分类号：O178

文献标志码：A