矩阵微分方程通解的待定矩阵法

吴幼明，梁丽枝，吴文峰（．佛山科学技术学院数学系，广东佛山58000；．爱荷华威斯莱大学商业管理系，爱荷华芒特普莱森特564）



矩阵微分方程通解的待定矩阵法

吴幼明1，梁丽枝1，吴文峰2
（1．佛山科学技术学院数学系，广东佛山528000；2．爱荷华威斯莱大学商业管理系，爱荷华芒特普莱森特52641）

摘要：基于矩阵微分方程理论，采用待定矩阵方法，推导了非齐次项为三角函数与指数函数乘积的一类常系数矩阵微分方程的通解公式。进行了2种特殊情况的讨论，利用算例验证矩阵微分方程通解公式的正确性。丰富了矩阵微分方程的解法理论。

关键词：矩阵微分方程；待定矩阵方法；通解

求矩阵微分方程的通解公式和特解公式［1-8］是矩阵微分方程理论的重要部分，但目前只有一阶矩阵微分方程研究结果比较丰富，而高阶矩阵微分方程研究结果还较少。对于高阶常系数线性矩阵微分方程来说，可用待定矩阵方法［3-5］求出矩阵微分方程的通解公式和特解公式。文献［6］给出了矩阵微分方程Af"（x）-Bf（x）=t（x）的通解公式，但t（x）仅为二次多项式情形，而文献［3］推导了文献［6］的方程在t（x）为三角函数与指数函数相乘形式的通解公式；文献［7-8］分别在文献［6］的基础上得到了矩阵微分方程Af"（x）-aAf′（x）-Bf（x）=t（x）和方程Af"（x）-Bf′（x）-Af（x）=t（x）的通解公式，对文献［6］作了推广，但t（x）也仅为二次多项式情形，而文献［4］推导了文献［7］的方程在t（x）为三角函数与指数函数相乘形式的通解公式，加深了文献［7］的结果。本文在文献［3，4，7，8］的基础上采用待定矩阵方法和按列比较方法，推导出了文献［8］的方程在t（x）为三角函数与指数函数相乘形式的通解公式，是文献［8］的纵向推广，亦是文献［3-4］的横向补充，更具有一般性。

1　符号

给出矩阵微分方程

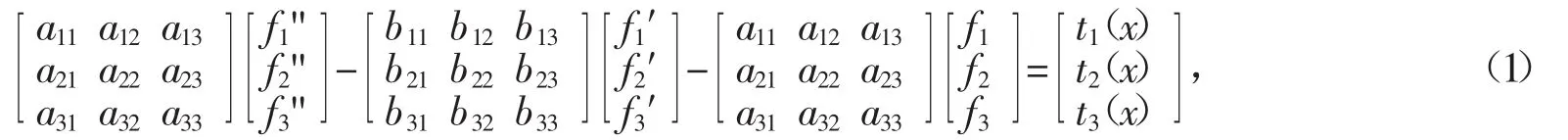
其中fi=fi（x）（i=1，2，3）是关于x的函数，ti（x）（i=1，2，3）是关于x的三角函数与指数函数的乘积，aij，bij（i，j=1，2，3）是常数。

因此，式（1）整理后为

2　方程的通解

2.1齐次方程的通解

方程（2）对应的齐次方程为

则方程（3）的通解［8］为，其中，而是矩阵C的3个特征根，V是矩阵C的列特征向量的矩阵，C1′、C2′是常数向量。

2.2非齐次方程的特解

对方程（2），设

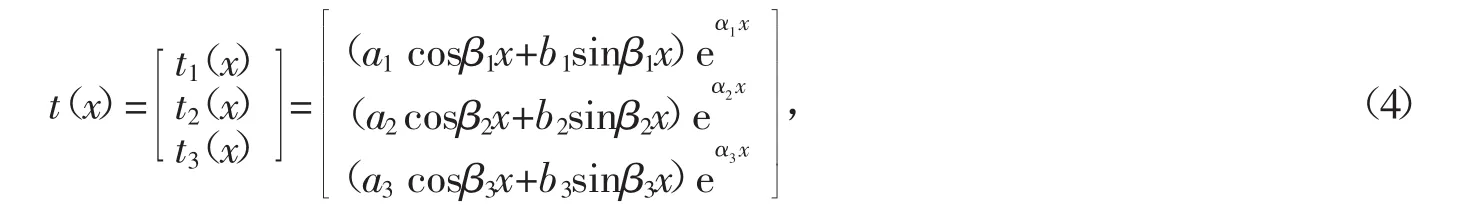
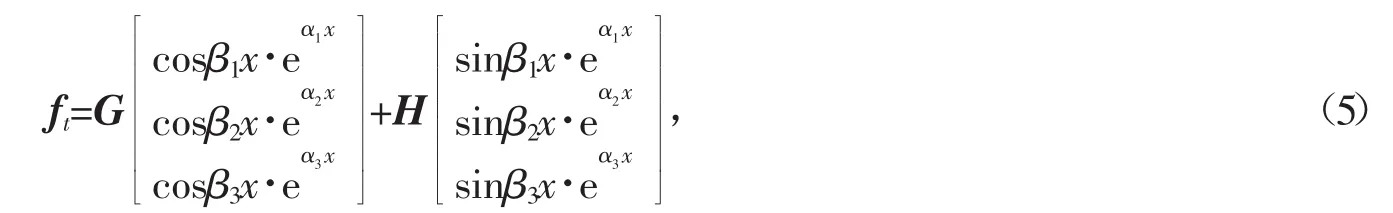
将式（5）代入方程（2），整理并比较相同三角函数的系数，得到下列2个等式

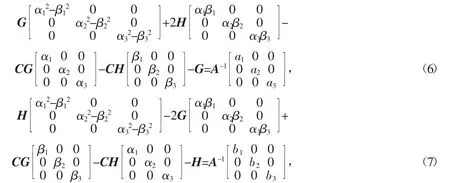
由式（6）取第i列得

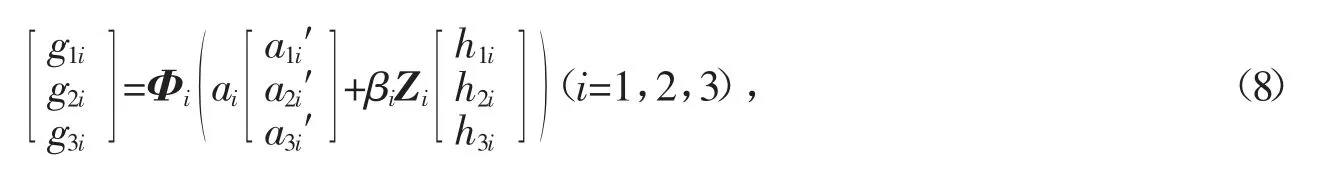
由式（7）取第i列得

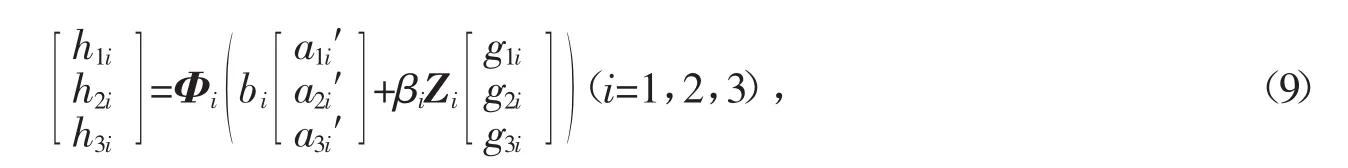
将式（8）代入式（9）并整理有

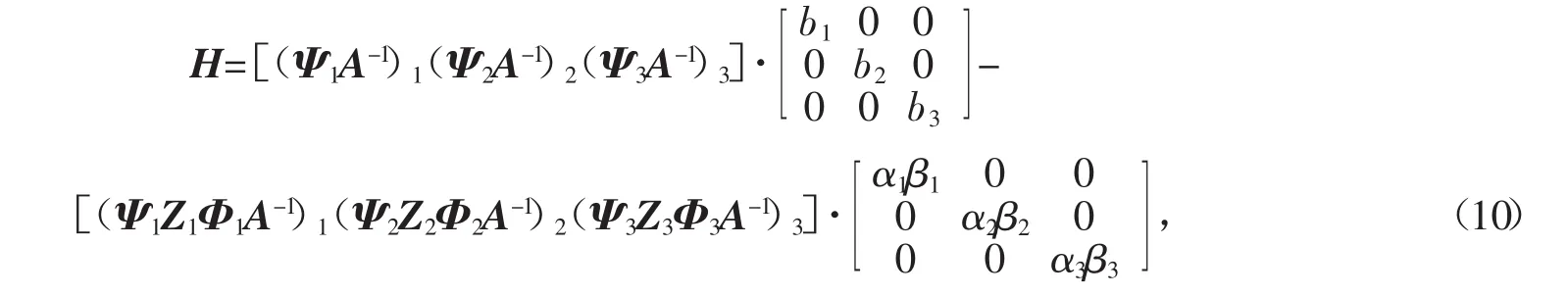
同理得

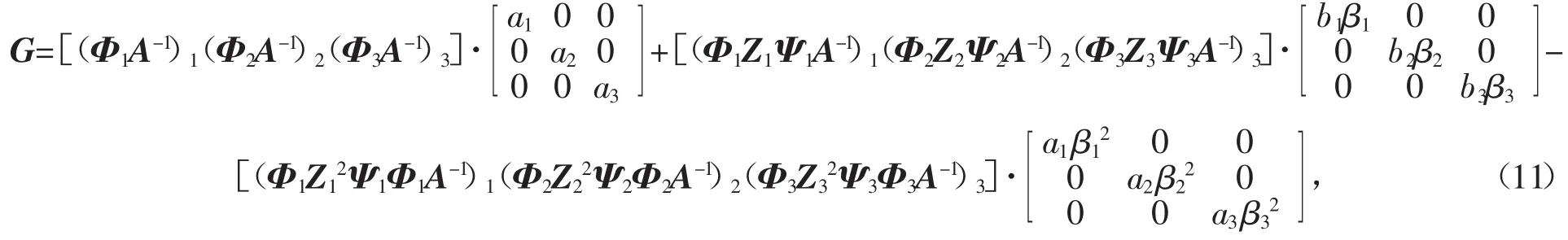
令

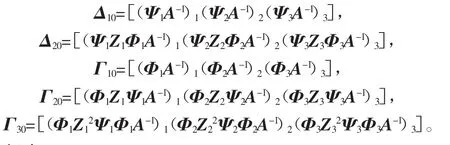
所以，方程（2）的一个特解为

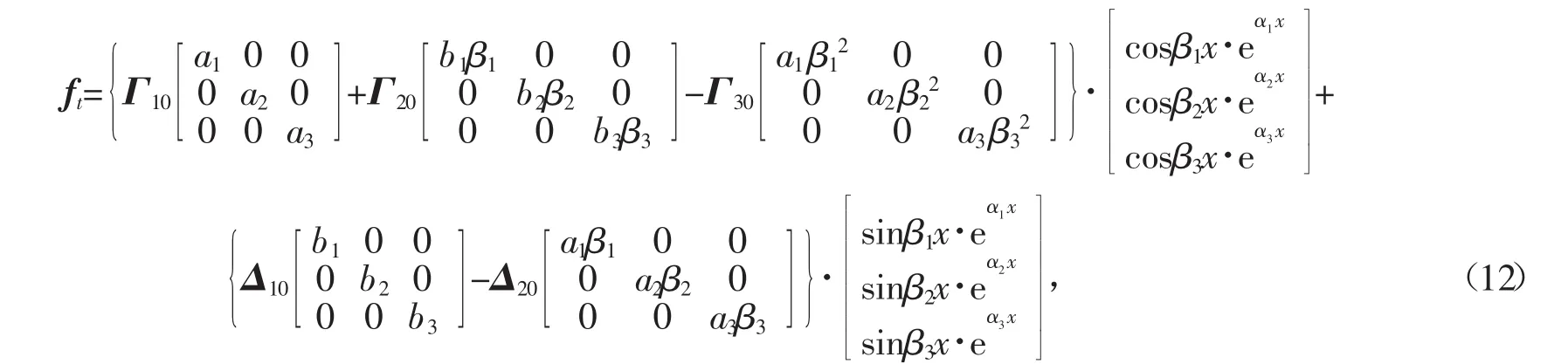
从而，方程（2）的通解为

2.3特殊情况的讨论

（1）当βi=0（i=1，2，3）时，式（12）变为

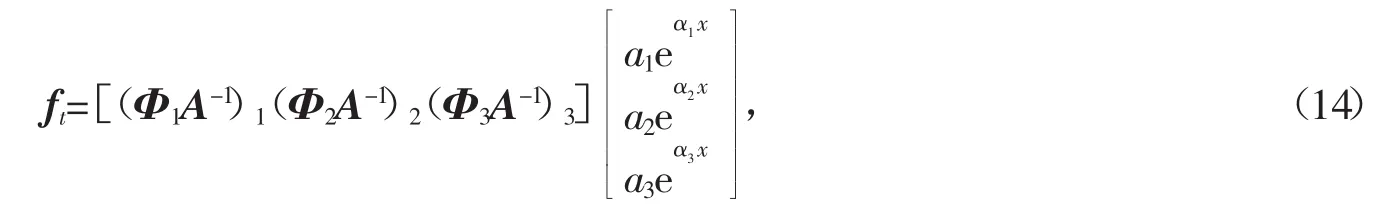
式（14）与文献［5］（当li=mi=0，i=1，2，3时）的结论完全一致，证明本文的公式是文献［5］的深化。

（2）当B=0时，式（12）简化后的结果与文献［3］当A=B时的结论完全一致，证明本文的公式是文献［3］的拓展。

3　算例

用本文方法解下列矩阵方程

其中

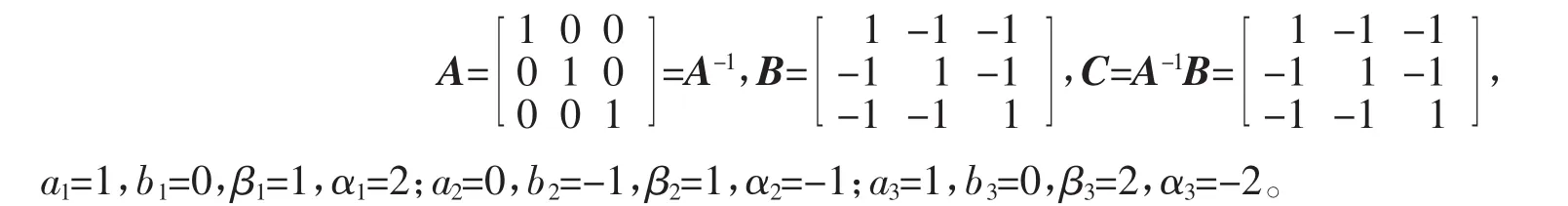
所以

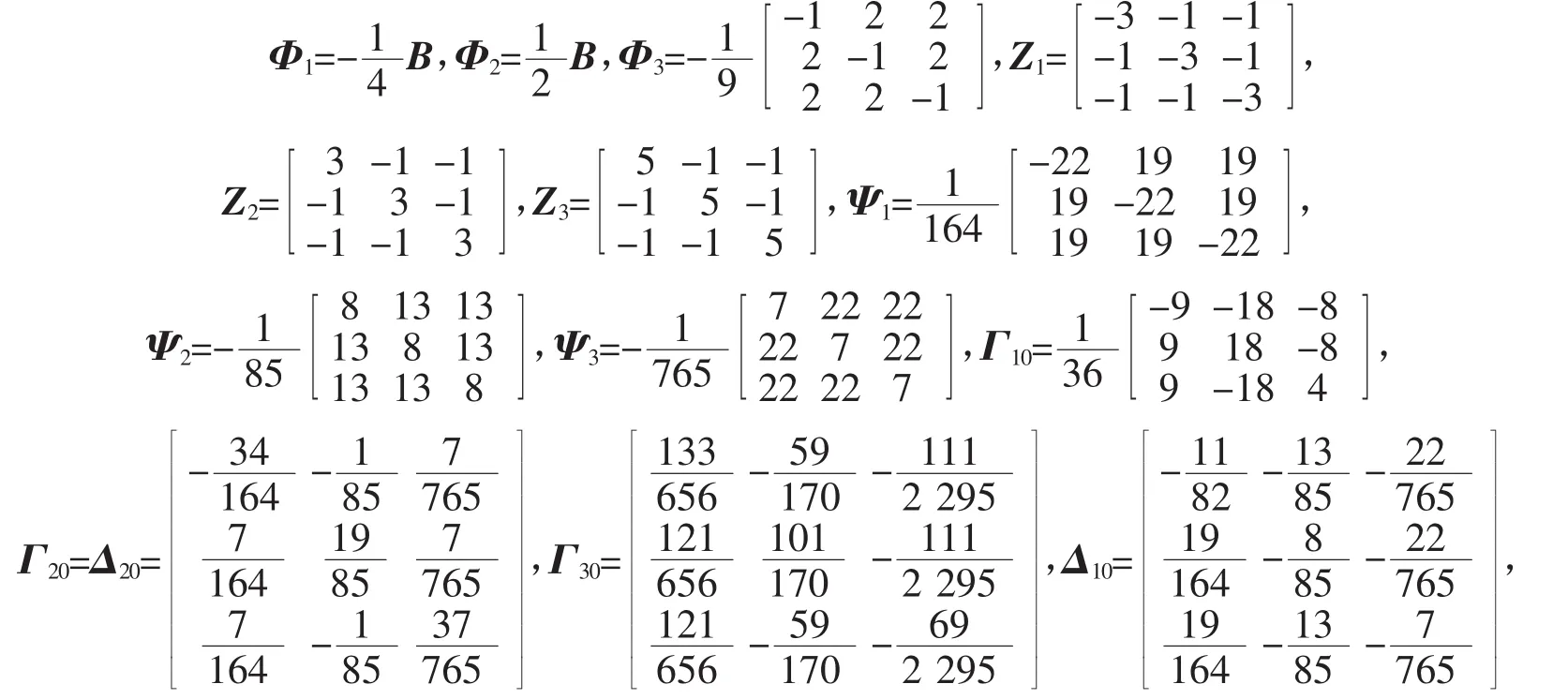
从而，矩阵方程（15）的1个特解为

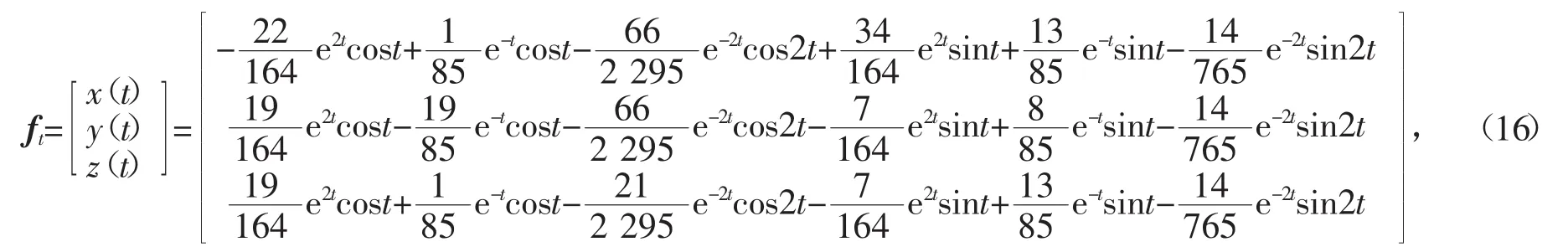
经检验，式（16）确是矩阵方程（15）的1个特解。

4　结语

本文采用待定矩阵法，得到了一类常系数矩阵微分方程的通解公式，但这是在假定矩阵的特征根互异的情况下得到的结论。矩阵的特征根是重根时的情况少见报道，尚有待进一步探讨。

参考文献：

［1］WU Y M, LUO Q Z, YUE Z F. Theoretical research of shear lag effect in thin walled box girder［C］//Proceedings of ICMEM, Nanjing:［s.n.］, 2005.

［2］黄建吾.二维二阶常系数齐线性微分方程组的一种解法［J］.福州大学学报:自然科学版, 2002, 30（1）: 20- 22.

［3］吴幼明,孔碧洁,何小媚.一类二阶常微分方程组的特解公式［J］.佛山科学技术学院学报:自然科学版, 2006, 24（4）: 7- 11.

［4］吴幼明,周单.一类二阶常微分方程组的特解［J］.佛山科学技术学院学报:自然科学版, 2011, 29（1）: 14- 19.

［5］吴幼明,吴文峰.一类二阶常微分方程组的特解［J］.四川理工学院学报:自然科学版, 2012, 25（6）: 61- 64.

［6］吴幼明,罗旗帜.一类二阶常系数微分方程组的通解［J］.佛山科学技术学院学报:自然科学版, 2002, 20（2）: 10- 14.

［7］吴幼明,王向东,岳珠峰.一类二阶微分方程组的通解［J］.汕头大学学报, 2007, 22（3）: 15- 20.

［8］吴幼明,卢永全,杜焕芬.一类二阶常微分方程组的通解［J］.佛山科学技术学院学报:自然科学版, 2009, 27（5）: 18- 22.

【责任编辑：王桂珍foshanwgzh@163.com】

Undetermined matrix method for the general solution of matrix differential equation

WUYou- ming1，LIANGLi- zhi1，WUWen- feng2
（1. Department of Mathematics, Foshan University, Foshan 528000, China; 2. Department of Business Administration, Iowa Wesleyan University, Mount Pleasant 52641, America）

Abstract:Based on matrix differential equation theory , and by the method of undetermined matrix , the paper is devoted to provide a general solution of finding a kind of matrix differential equation with constant coefficients, and the non- homogeneous terms of matrix differential equation are the form of the trigonometric functions multiplied by exponential function. The special cases are discussed in detail. For example, the general solution formulas are validated. It is shown that the present method of solving on matrix differential equation is effective and general.

Keywords:matrixdifferential equation; method ofundetermined matrix; general solution

作者简介：吴幼明（1962-），男，广东广州人，佛山科学技术学院副教授，博士。

基金项目：广东省自然科学基金资助项目（S2013010012463）

收稿日期：2015-09-11

文章编号：1008- 0171（2016）02- 0001- 04

中图分类号：O151.21

文献标志码：A