一类超线性Schrödinger方程非平凡解的存在性
2016-04-21郭艾李晓丹华南理工大学数学学院广东广州510640
郭艾,李晓丹(华南理工大学数学学院,广东广州510640)
一类超线性Schrödinger方程非平凡解的存在性
郭艾,李晓丹
(华南理工大学数学学院,广东广州510640)
摘要:通过变量代换,将超线性Schrödinger方程转变为较简单的椭圆型方程,然后利用山路引理证明了此问题存在一个非平凡解。
关键词:Schrödinger方程;山路引理;非平凡解
研究下面Schrödinger方程解的存在性

其中f(x,u)是关于x的1周期函数。
(V0)对所有的x∈RN,V(x)≥V0;
(V1)对所有的是一个Hölder连续函数,并且满足:
(f1)当s→0+,在RN中一致有
(f2)存在常数a1,a2>0和2<q<2*使得对所有的(x,s)∈RN×[0,+∞);
(f3)存在一个常数函数使得,对所有的,其中并且p≤q;
(f4)当,在RN中一致有
定理假设N≥3,则方程(1)有一个非平凡解。
显然方程(1)的解是下面泛函的临界点
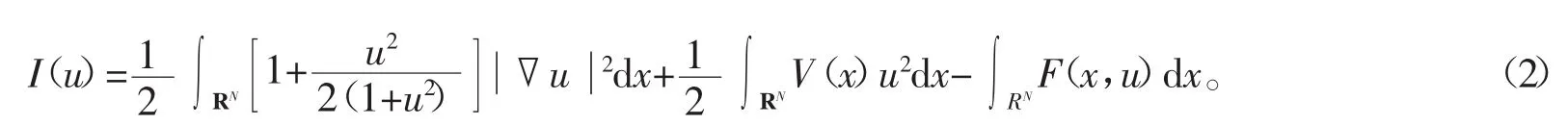
由于泛函I(u)在一般的Sobolev空间H1(RN)没有定义,所以进行如下变量代换

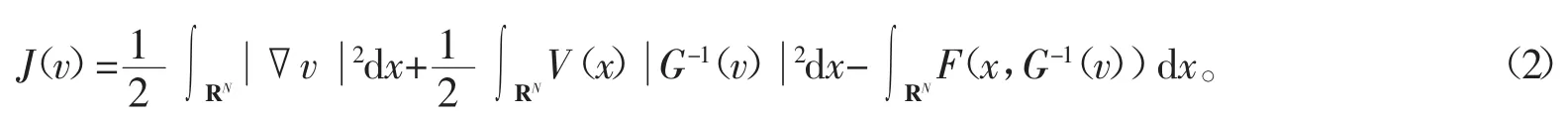

则式(3)就相当于
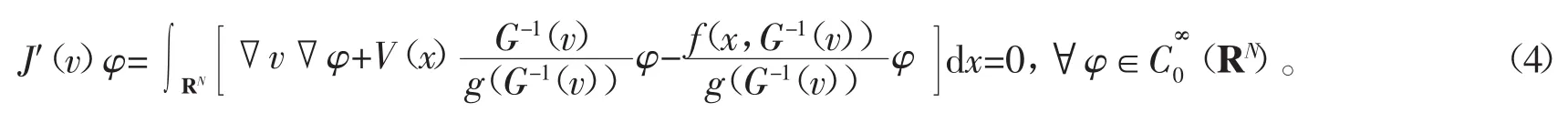

在证明定理之前,首先给出一些相关的引理。
引理1对所有t≥0,有

证明见文献[1-3]。
接下来,建立山路引理的几何条件。
引理2存在ρ0,a0>0使得对所有的有J(v)≥a0。
证明因为

由(f1)和(f2),对任意ε>0,存在一个常数Cε>0,使得

从而

由(V0),可以得到
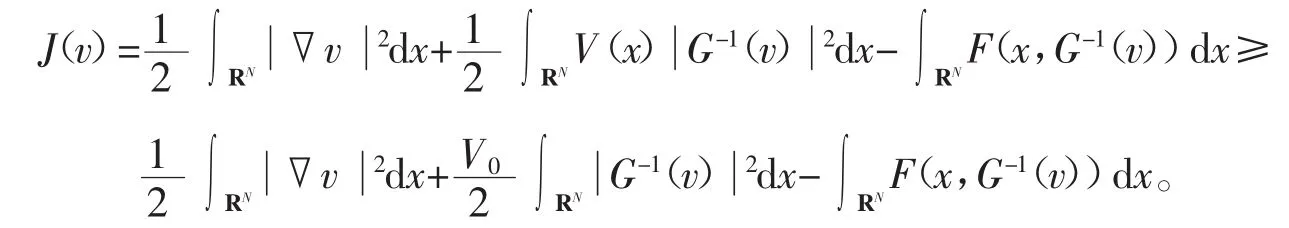
令

通过引理1和(f1),有
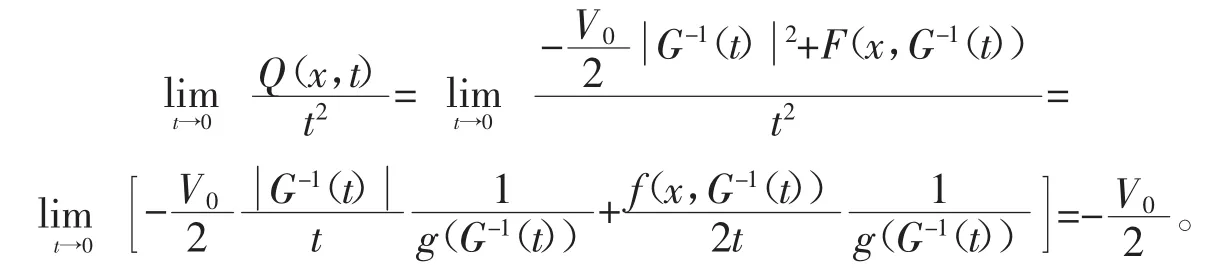
同样,通过引理1和(f1),有

于是,对充分小的ε>0,存在一个常数Cε>0,满足

那么,有

通过选择适当小的ρ,当‖v‖=ρ时,得到引理2。

由(f4)得即J(tø)→-∞,当t→∞时。因此,引理3得证。
在A-R山路引理2和引理3的结果中,对于常数

其中

在水平值c处存在一个P-S序列,即当n→∞时,J(vn)→c且J′(vn)→0[4-5]。


且

因此


令0<δ 即 由(f3),有 由式(6)可知,存在常数C1,使得 由(f2)知道p≥q,当p=q时,由式(9)、(10)可以得出式(7)成立。当p 接下来给出定理的完整证明。 证明首先,证明J′(vn)=0,也就是证明v是方程(1)的一个弱解。由引理4,知道是一个有界的P-S序列,因此存在在中满足vn弱收敛于v,则由Lebesgue控制理论,可得 于是J′(vn)=0,v是方程(1)的一个弱解。接下来要证明v≠0,用反证法,假设v=0,分3步来证明假设不成立。 由G-1(t)≤g(G-1(t))t,得 假设 令q=λ(2+p)+(1-λ)(2*-p),λ∈(0,1),由Hölder不等式和引理1,得 因为2<2+β,2*-β<2*,则由式(5)、(10)和引理1得,对任意ε>0,有 由式(11)和J′(vn)vn→0可以得到 由引理1得 从而 由式(12)和(13)知,J(vn)→0,这与J(vn)→c>0矛盾。因此不会消失,即存在使得 其中 并且 2J∞(vˆ)-J′∞(vˆ)vˆ=2J∞(vˆ)。 由c∞的定义知 如果V(x)≡V(∞),则证明了定理1;如果V(x)≤V(∞),但V(x)≡V(∞)不成立,由路径Γ,有 矛盾,因此,v是一个非平凡解。 参考文献: [1]CHENG K, YAO Y. Solition solutions to a class relativistic nonlinear schrödinger equation[J]. Appl Math and Comp, 2015, 260: 342- 350. [2]LIUJ Q, WANGZQ. Soliton solutions for quasilinear Schrödinger equations[J]. Proc Amer Math Soc, 2003, 131: 441- 448. [3]LIU J Q, WANG Y Q, WANG Z Q. Soliton solutions for quasilinear schrödinger equationsⅡ[J]. J Differential Equation, 2003, 187: 473- 493. [4]ZHOU Huansong. Positive solution for a semilinear elliptic equation which is almost linear at infinity[J]. Z Angew Math Phys, 1998, 49: 896- 906. [5]ELVESA, SILVAB, GILBERTOF. Vieira, quasilinear asymptoticallyperiodic schrödinger equation with subcritical growth[J]. Nonlinear Analysis, 2010, 72: 2935- 2949. [6]RRTHER W. Bifurcation for a semilinear elliptic equation on RNwith radiallysymmetric coefficients[J]. Manuscripta Math, 1989, 65: 413- 426. [7]COLINM, JEANJEANL. Solutions for a quasilinear Schrödinger equations: Adual approach[J]. Nonlinear Anal TMA, 2004, 56(2): 213- 226. 【责任编辑:王桂珍foshanwgzh@163.com】 The existence of nontrivial solution to a class of superlinear Schrödinger equation GUOAi, LI Xiao- dan Abstract:Usinga change ofvariable, we concert a class ofsuperlinear Schrödinger equation into a simple elliptic one. Byusing Mountain pass Lemma, we showthe existence of nontrivial solution for a Schrodinger equation. Keywords:Schrödinger equation; mountain pass theorem; nontrivial solution 作者简介:郭艾(1962-),女,广东广州人,华南理工大学教授,博士。 基金项目:国家自然科学基金资助项目(11461014) 收稿日期:2015-08-03 文章编号:1008- 0171(2016)02- 0005- 07 中图分类号:O241.6 文献标志码:A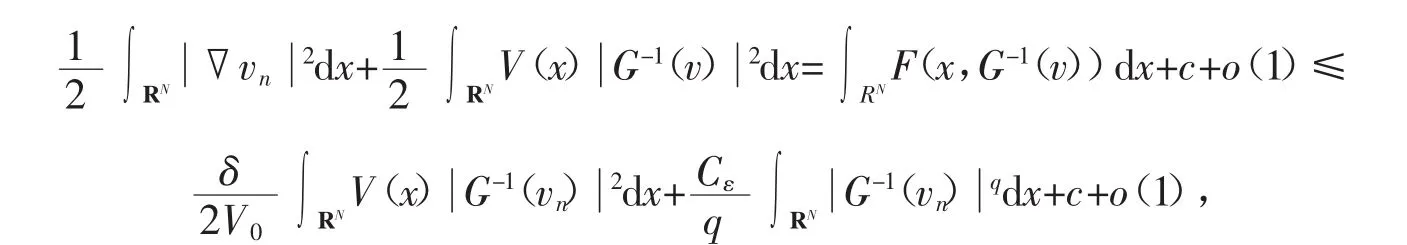
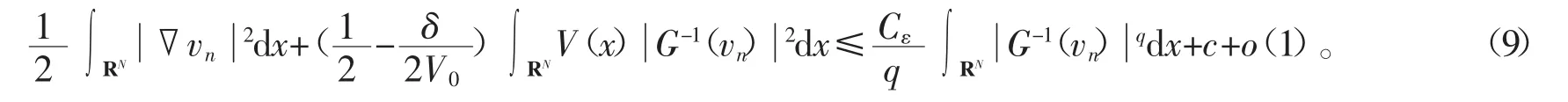
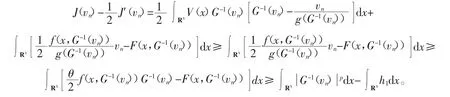

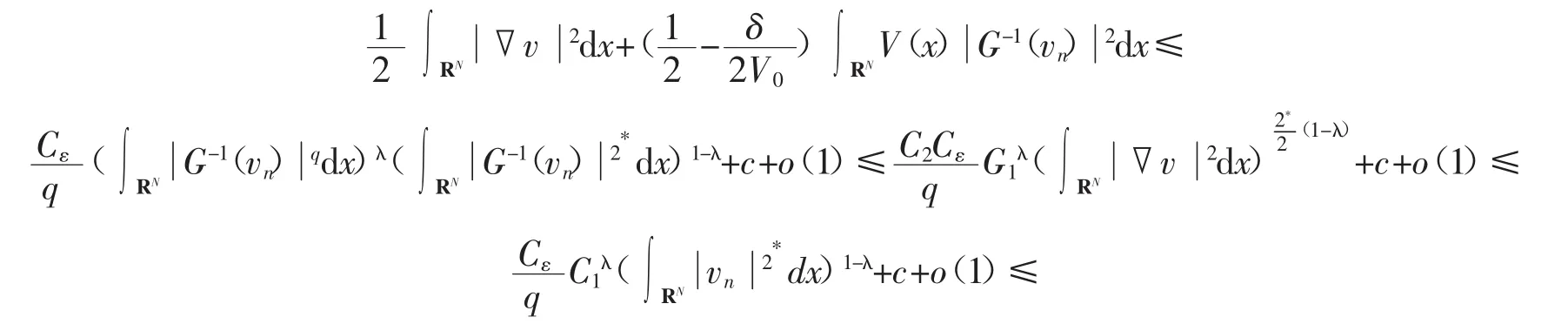

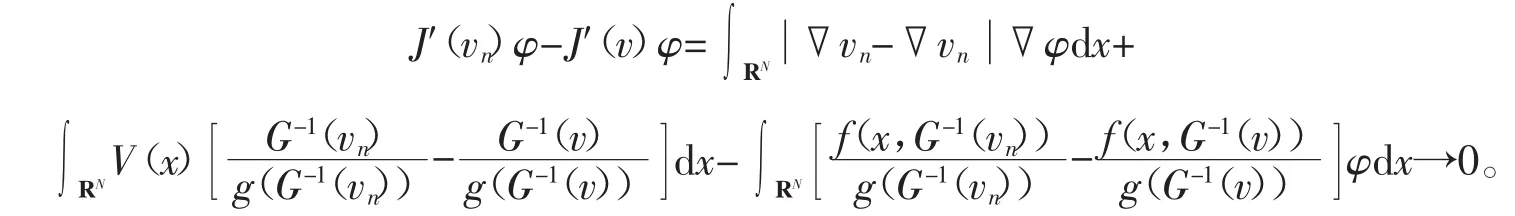







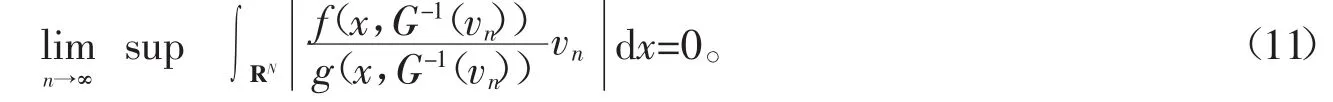





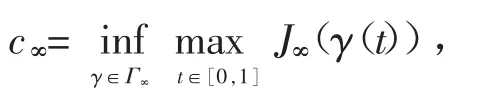




(School of Mathematics, South China Universityof Technology, Guangzhou 510640, China)
