自重、渗流及地震耦合作用下人工岛动力稳定性分析

赖　杰, 郑颖人, 李秀地, 刘　云(.后勤工程学院 军事土木工程系，重庆　03；2. 重庆市地质灾害防治工程技术研究中心，重庆　000；3.岩土力学与地质环境保护重庆市重点试验室，重庆　03；. 重庆交通大学 土木工程学院，重庆　0007)



自重、渗流及地震耦合作用下人工岛动力稳定性分析

赖杰1,3, 郑颖人1,2, 李秀地1, 刘云4(1.后勤工程学院 军事土木工程系，重庆401311；2. 重庆市地质灾害防治工程技术研究中心，重庆400041；3.岩土力学与地质环境保护重庆市重点试验室，重庆401311；4. 重庆交通大学 土木工程学院，重庆400074)

摘要：针对人工岛在自重、渗流、地震等耦合作用下动力稳定性研究较少的现状，以某人工岛边坡为例，首次将强度折减动力分析法引入到人工岛动力稳定性分析中，建立有限元数值分析模型，采用Finn-Byrne和修正Hardin-Drnevich动力本构，对多场耦合作用下人工岛液化范围、受力情况及动力稳定性进行分析。计算表明：① 在设防烈度地震作用下，人工岛能够满足动力稳定性要求，由于海底淤泥层抗剪强度很低，地震下的最终破裂面由抛填块石下部与淤泥层共同组成；② 岛内侧降水，使得海水渗流方向由岛外指向岛内，增加岛外侧土体有效应力，提高其抗液化能力，降低了岛内土体的有效应力，因此地震作用下内侧土体更易液化；③ 由于受到周围土体的约束作用，土体局部液化不会产生液化大变形，只有液化土体较多才会产生大变形。研究结果为人工岛动力分析提供参考。

关键词：人工岛；渗流；强度折减动力分析法；液化

随着我国经济不断发展，陆地交通日益紧张，加之海岸线长、岛屿众多，发展海上交通通道具有重要的政治、经济意义，势在必行。由于人工岛位于远离陆地的海域，环境恶劣、工程条件复杂，受外海的波浪、潮位、深厚软土、地震等影响很大，给工程建设带来极大的难题，开展人工岛在施工期、使用期的安全稳定性研究具有重大意义[1-2]。

加之我国近海人工岛多处于环太平洋地震带，地震灾害频繁，而大型人工岛建设处于起步阶段，人工岛相关研究主要集中于施工工艺[1]、砂土液化[2]、防浪结构[3-5]、静力作用下稳定分析[6-8]等方面，对动力稳定性的相关研究很少，严重滞后于工程实践，影响工程建设成败。基于此，文章结合东海某人工岛工程，考虑了渗流、地震和自重等多种作用的影响，结合FLAC3D软件利用有限元强度折减动力分析法[9-10]，首次对人工岛使用期的动力稳定性进行分析，研究结果为我国南海填海造岛、跨海工程建设提供重要参考。

1流固耦合介绍

在满足Biot固结方程[11-12]条件下，FLAC3D软件采用可以考虑流体与土颗粒之间相互作用的Darcy定律，其基本方程如下：

1.1渗流平衡方程

(1)

式中：qi为渗流速度;qv为流体源强度;ζ为单位体积孔隙介质的流体体积变化量;M为比奥模量;p为孔隙水压力;a为比奥系数;ε为体积应变;T为温度;t为时间;β为考虑流体和固体颗粒的热膨胀系数。由于人工岛处于近海，温度变化相对较小，对人工岛的稳定性、变形和结构受力影响不大，因此文章只针对渗流、自重以及地震的耦合作用，没有考虑温度场的影响，此时∂T/∂t=0。

1.2渗流运动方程(广义达西定律)

(2)

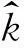
1.3流固耦合方程

(3)

1.4相容性方程

εij=0.5(vi,j+vj,i)

(4)

式中：v为某点速度

1.5边界条件

qn=h(p-pe)

(5)

式中：Pe为渗流出口处的孔隙水压力；qn是边界处流速外法向分量；P为边界面处的孔隙水压力；h为渗漏系数。

2动力本构

2.1Martin-Finn-Byrne动力本构模型

Martin[13]通过大量试验得到了动力作用下每次循环荷载的体应变增量Δεvd与剪应γd及体应变εvd之间的关系，如

(6)

在Martin基础上，Byrne[14]提出一种更为简单的形式：

(7)

式中：系数C1、C2与标准贯入锤击数N或相对密实度Dr之间有关。

2.2修正Hardin-Drnevich模型

针对黏性土体则采用修正Hardin-Drnevich模型[12,15,16]，由于传统的Hardin-Drnevich黏弹性模型存在不能考虑土体永久变形的缺陷，FLAC3D软件将其与Mohr-Coulomb准则结合在一起，可以考虑土体的永久变形，弥补了前者的不足，修正后的应力-应变曲线如图1所示。

图1　修正后的应力-应变曲线Fig.1 Revised stress-strain curve

在弹性阶段，剪应变幅值γc<γm时，存在着：

(8)

(9)

在塑性阶段，剪应变幅值γc≥γm时，满足：

(10)

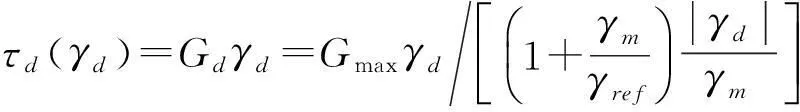
(11)

式中，τd动剪应力，γd为动剪应变，Gd为动剪切模量，Gmax为最大剪切模量，γref=τm/Gmax，τm为循环最大动剪应力。

3强度折减动力分析法

郑颖人等[9-10]依据地震作用下边坡破坏特征，采用一种新的计算边坡动力稳定性方法-强度折减动力分析法，该法可以考虑岩土体在地震作用下的拉-剪破坏，更能符合实际。传统边坡静力稳定分析根据力 (矩)的平衡来计算安全系数，将安全系数定义为滑动面的抗滑力(矩)与下滑力(矩)之比：

(12)

在强度折减法中，将上式两边同时除以ω，降低抗滑力，使得边坡进入极限状态(安全系数为1)，此时的折减系数ω就为边坡安全系数。

(13)

在地震往复作用下，边坡破坏由受拉和受剪复合破坏组成，在强度折减时还需考虑岩土体抗拉强度的折减[9]：

σt′=σt/w

(14)

式中，ω为折减系数，c为黏聚力，σt为抗拉强度，φ为内摩擦角，c′、σt′、φ′为强度折减到破坏时的值。采用强度折减动力分析法进行边坡的动力安全性分析时，主要从以下三个方面对边坡是否失稳破坏进行综合判断：① 看拉破坏区与剪切塑性区是否贯通，但贯通是必要条件而非充分条件；② 看监测点位移是否突变，考虑地震荷载随时变化，监测点的位移也随时发生变化，因此与静力问题不同，地震中的单一时刻发生突变并不能判断边坡破坏，但地震完后的最终位移发生突变，仍然可以作为破坏的判据；③ 分析地震结束后，监测点位移及受力是否收敛，若不收敛表明地震后坡体已经失稳破坏。

4人工岛算例

4.1人工岛基本情况

某人工岛区域海底地形平缓，地貌形态较为简单，底层从上到下主要由淤泥、淤泥质黏土、粉质黏土、黏土组成，岸壁结构采用插入式钢圆筒外侧辅以抛石斜坡堤结构方案，钢圆筒长40 m, 直径采用22 m，厚度16 mm，筒顶标高为3.5 m，海底淤泥顶部标高为-8 m，筒底标高以持力层和施工期的止水功能为准，本算例为-36.5 m。10年一遇的高水位为2.57 m，20年一遇高水位为2.97 m，海床顶部标高为-8.5 m。

4.2阻尼选取及物理参数

在进行动力计算时，由于实际解决的为半无限空间问题，计算网格需要无限大，而实际计算为有限网格，为消除地震波在有限的人工边界上的反射效应，通过自由场与粘性边界的耦合来吸收平面波的能量，以模拟无限远边界。计算采用的阻尼形式为FLAC3D中的局部阻尼[11]，因为能量损失ΔW/W与频率及应变率无关，而与临界阻尼比D有关，可以得到局部阻尼系数al的表达式：

al=πD

(15)

进行数值模拟时采用局部阻尼，对于岩土材料而言阻尼比为2%～5%[5]，对于结构体而言为2%～10%，本文土体阻尼比取5%，钢圆筒的阻尼比为3%。在人工岛边坡共设置A1～F5监测点，具体位置如图2所示。

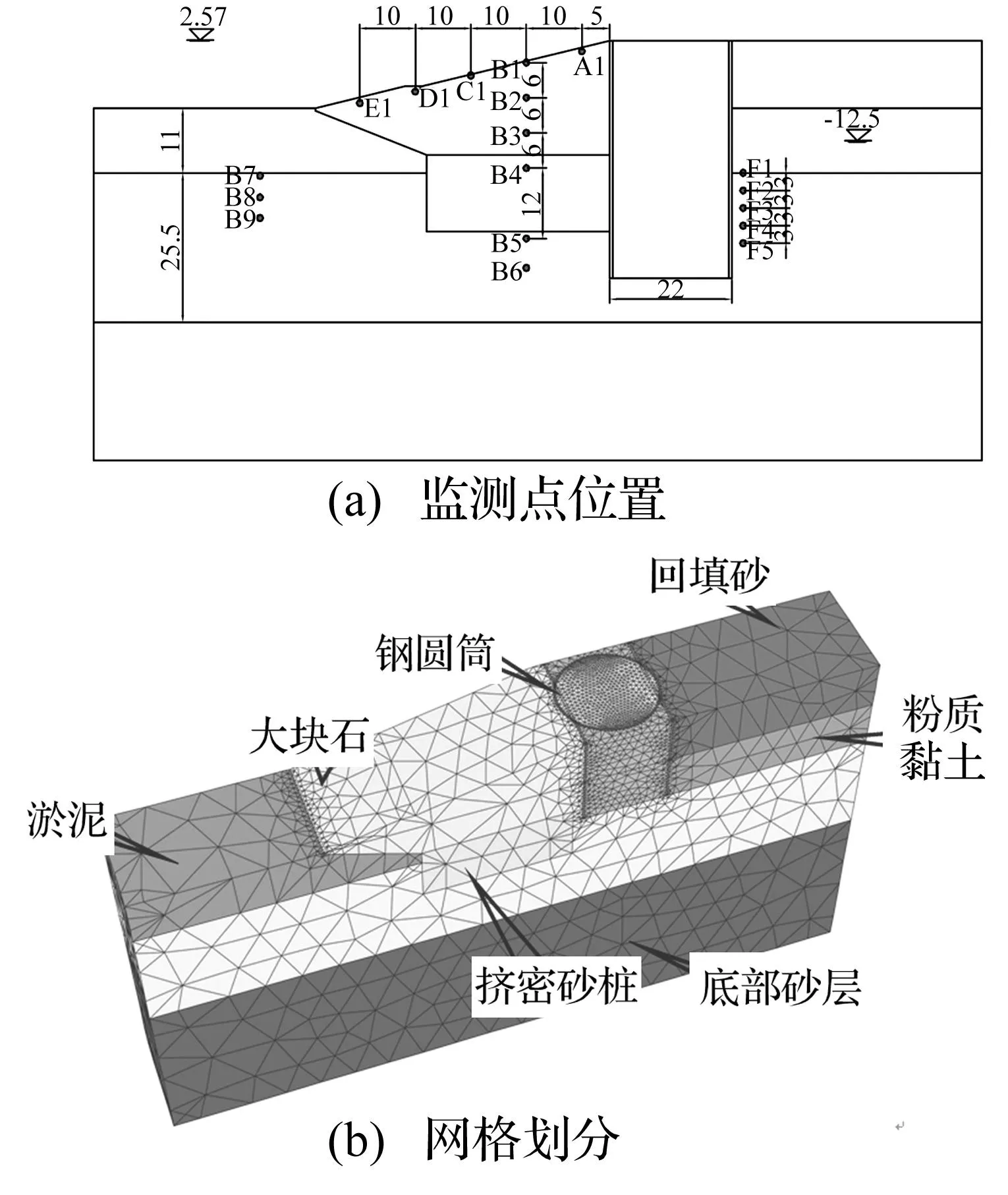
图2　人工岛边坡计算模型示意图Fig.2 Calculation model for the artificial island slope

计算模型长220 m,高112.5 m。人工岛外侧水位选用10年一遇的高水位(标高2.57 m)，人工岛岛内人工抽水水位为-12.5 m。为提高计算效率、减小网格大小，选取典型截面进行计算，总网格单元数15.95万个，圆筒与周围土体之间通过设置接触单元Interface来模拟相互作用，接触面单元满足摩尔-库伦准则，其抗剪强度cinter和φinter为圆筒周围土体的0.8倍。计算中考虑置换砂、挤密砂桩和底部砂层为可液化土层，参数如下表所示。

表1　材料的物理力学参数

表2　材料渗流及液化计算参数

4.3输入的地震波

人工岛所处地区基本烈度为7度，由于该工程为重要的民生工程，战略位置、经济地位重要，需提高一度进行抗震设计。数值计算采用峰值分别为0.2 g和0.3 g的双向Kobe波(日本，1995，竖直向峰值为水平向峰值的1/2，震源位于近海海域)进行计算，其中圆筒桩受力、块石加速度响应和人工岛稳定性采用0.2 g地震波；人工岛液化分析则采用0.2 g和0.3 g两种情况进行分析。输入地震波位置为模型底部，水平向为边坡倾向，波形如图3所示。

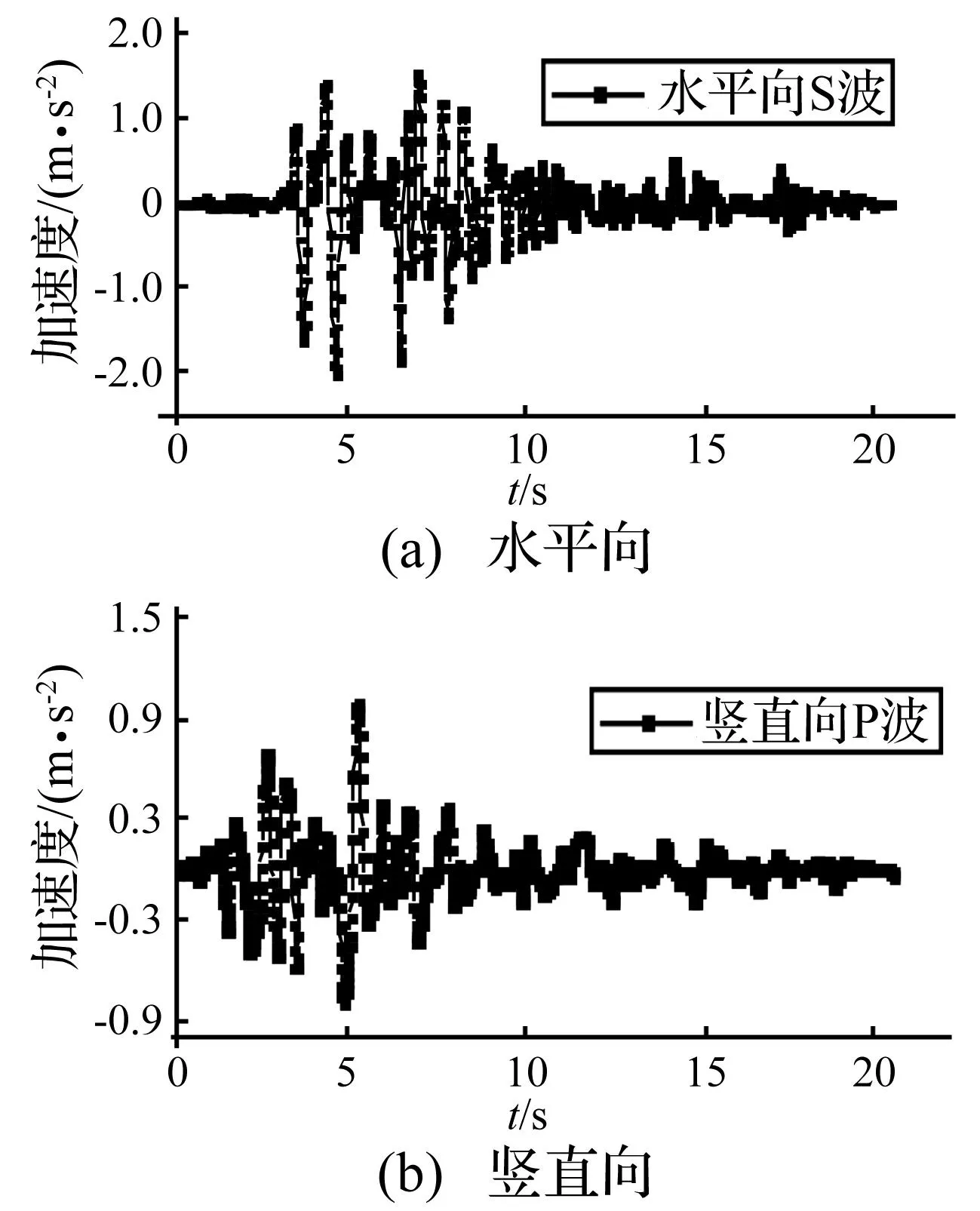
图3　输入地震波(Kobe波)Fig.3 Input earthquakes(Kobe wave)

4.4圆筒受力分析

在钢圆筒内外两侧从筒顶以下每隔3 m设置一个监测点，记录每个监测点的动土压力时程曲线，选取动土压力较为明显的几个时刻进行分析，其分布形式如图4所示。

图4　地震作用下钢圆筒两侧受力分布Fig.4 Dynamic earth pressure distribution on both sides of Steel drum triggered by earthquake

由地震作用下钢圆筒两侧受力分布情况可知(见图4)，筒的埋深越深，动土压力越大；在地震4 s～6 s峰值时刻附近，钢圆筒两侧动土压力响应最为明显。

4.5人工岛稳定性分析

4.5.1高水位下的稳定分析与破裂面位置

当岛外海水高水位为2.57 m，岛内-12.5 m时，采用强度折减动力分析法[9]对人工岛边坡进行动力稳定性分析。当折减系数为1.26时(图5(a))，从监测点A3的位移时程曲线上看，其最终位移保持不变，计算收敛，此时人工岛边坡还处于稳定状态；当折减系数为1.27时(图5(b))，监测点的最终位移不收敛，表明震后边坡失稳破坏。据此可知该水位下人工岛边坡动力安全系数为1.26。

图5　监测点折减系数与位移关系曲线Fig.5 Reduction factor-displacement curve for monitoring points

图6为剪切应变增量云图，当折减系数为1.26时，此时剪切塑性区已经贯通，边坡临近破坏状态，与监测点的位移时程曲线相吻合，此时出现的拉破坏单元很少，主要以剪切破坏为主。由上图可见，人工岛最终破裂面为抛填块石及下部的淤泥层共同组成，如图中红线所示。

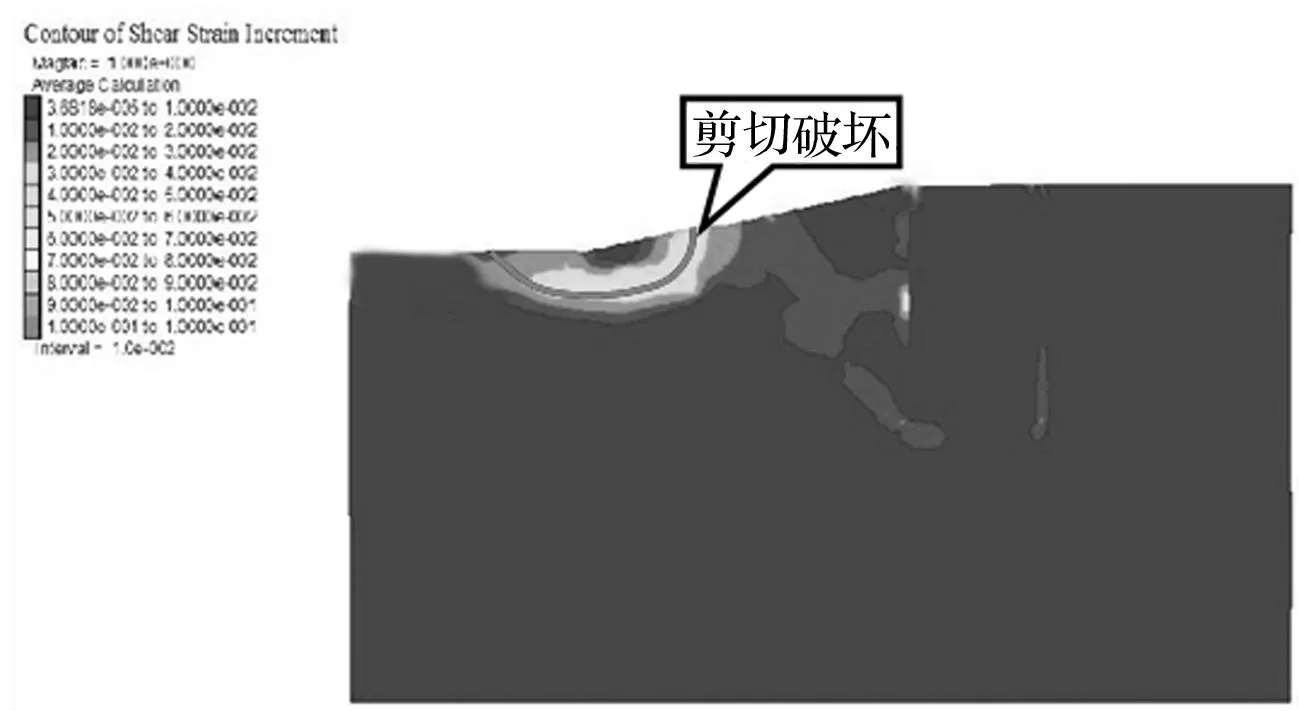
图6　剪切应变增量云图(折减1.26)Fig.6 Shear plastic Nephogram (Reduction is 1.26)

4.5.2低水位下的稳定分析与破裂面位置

当海水处于低水位-0.93m，岛内-12.5m时，采用强度折减动力分析法，得到动力安全系数为1.21，同样满足安全要求。由于水位降低，抛填块石的顶部将失去水压作用，同时块石的抗拉强度很低，地震作用下将产生受拉破坏(见图7(a))，滑坡的最终破坏滑动面由上部的拉破坏和下部的剪切破坏组成，如图7中红线所示。此时边坡稳定性比高水位时低，破坏区大，主要原因在于：一是边坡失去水压的有利作用；二是人工岛内外存在水位差，渗流从左到右(岛外向岛内)流动，尽管不利于岛内土体的稳定，但却有利于岛外边坡土体的稳定，低水位导致这种有利的渗流作用降低，致使边坡稳定性降低。

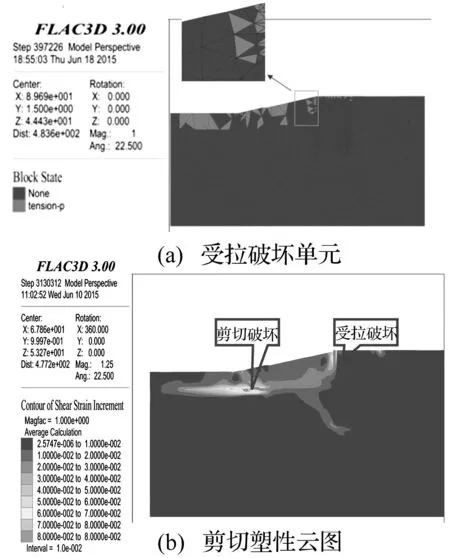
图7　人工岛水位下降后破坏面位置(低水位-0.93 m)Fig.7 Shear plastic Nephogram (Reduction is 1.20)

4.6孔隙水压力分析

4.6.1孔压比

当土体发生液化时，有效应力σ′=0，即总应力满足σ1=σ2=σ3=u，u为孔隙水压力。一般采用超孔隙水压比ru来描述土体液化情况，其中ru满足：

(16)

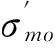
4.6.2监测点孔隙水压力分析

当输入地震波峰值为0.2 g时，未发现液化单元，人工岛没有发生液化现象；采用峰值为0.3 g地震波时，从单元液化状态图(见图8)上看，在6 s时刻地震峰值附近有液化单元产生，随着地震作用减小，孔隙水压力逐渐消散，地震结束后土体不再液化。因下卧砂层受到地震和渗流的共同作用，岛外水位高(左侧)，岛内水位低，钢圆筒左侧受到向下渗流的作用，使得自重有效应力增加，液化难度增大，而右侧受到向上的渗流作用，自重有效应力降低，地震作用下更易液化。

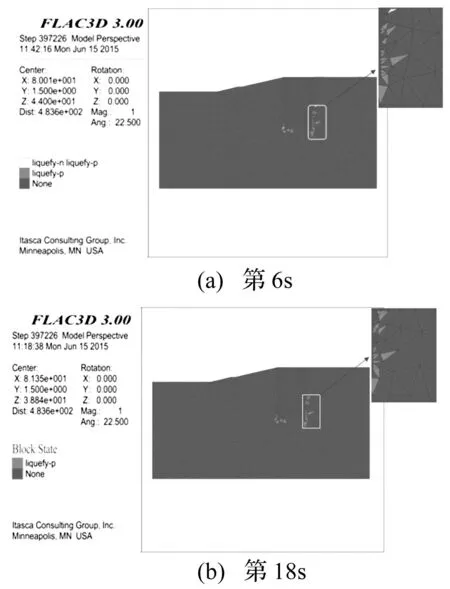
图8　单元液化状态图Fig.8 Unit liquefaction state

由于液化单元状态图并不能显示人工岛外侧(左侧)土体接近液化的状态，因此设置监测点B7、B8(见图2(a))监测该处的有效应力时程曲线、孔隙水压力以及对应的超孔隙水压力比。图9表明：地震作用下土体有效应力降低(FLAC3D中土压力为负值，孔隙水压力为正值)，由于作用时间短且砂土上覆较厚的非液化土层，水来不及排出，孔隙水压力不断增长；在4 s～10 s之间地震作用最为强烈时，土体有效应力降低很快，接近“完全失重状态”，10 s后有效应力稍有恢复后保存稳定；孔隙水压力和超孔隙水压比也对地震波作用时刻很敏感，当地震作用在峰值附近波动时，孔隙水压力增长迅速，超孔隙水压力比最高值在0.85与1.0之间，按公式(15)意义可知人工岛外侧土体临近液化。

从岛内外侧孔隙水压力分析表明：设防烈度地震(0.2 g)作用下，人工岛边坡不会发生液化，在遭遇0.3 g时，岛内侧土体部分液化，岛外侧土体临近液化，不会产生液化大变形，人工岛满足安全要求。

(a) B7、B8有效应力(b) B7、B8孔隙水压力(c) B7、B8监测点超孔隙水压比图9 监测点B7、B8的孔隙水压力及超孔隙水压力比时程曲线Fig.9Time-historyofPorewaterpressureandexcessporewaterpressureratioforB7,andB8

5结论

(1) 利用强度折减动力分析法得到人工岛在8度(0.2 g)高水位的地震下安全系数为1.26，低水位动力安全系数为1.21，满足设计要求。人工岛地震作用下的最易破坏位置在边坡抛填块石下侧，高水位时破坏范围小，低水位时破坏范围大。

(2) 人工岛建成后，岛内外存在15 m左右的水头差，渗流作用使得岛外侧土体有效应力增加，岛内侧有效应力降低。依据渗流分析，靠近钢圆筒处水力坡降最大，有效应力降低最多，因此受到地震作用时，右侧岛内土体更易液化。

(3) 数值模拟表明，当人工岛遭遇8度(0.2 g)地震作用时，土体不会发生液化。在基本烈度8度强(0.3 g)地震作用下部分土体发生液化，但由于只有少数土体液化，液化时间短，同时受到周围非液化土体约束作用，人工岛不会发生液化大变形。

参 考 文 献

[ 1 ] 王彦林，吴泽生. 港珠澳大桥东、西人工岛施工图设计安全风险评估[J]. 施工技术,2013,42(11):64-68.

WANG Yan-lin，WU Ze-sheng. Risk assessment for the construction drawing design of the east and west artificial islands of Hong Kong-Zhuhai-Macao bridge[J]. Construction Technology, 2013,42(11):64-68.

[ 2 ] Liam F W D， Ventura Carlos E, Wu Guo-xi. Analysis of ground motions at Treasure Island site during the 1989 Loma Prieta earthquake[J].Soil Dynamics and Earthquake Engineering,1993,12(7):383-390.

[ 3 ] 刘海笑，王仲捷. 结构-波浪-海床藕合系统中大圆筒结构的波压力响应[J].水利学报,2003(4):67-74.

LIU Hai-xiao, WANG Zhong-jie. Wave pressure response of large cylindrical structures in seabed-wave-structure coupling system[J].Journal of Hydraulic Engineering, 2003(4):67-74.

[ 4 ] 肖忠. 软土地基上新型防波堤结构的稳定性分析[D].天津:天津大学，2009.

[ 5 ] 房卓. 梳式防波堤的水动力学特性研究[D].辽宁：大连理工大学，2011.

[ 6 ] 王公伯，李广雪，徐继尚. 近海人工岛稳定评价方法体系的研究[J].海洋地质与第四纪地质,2011,31(4):83-88.

WANG Gong-bo, LI Guang-xue, XU Ji-shang. A Stability evaluation system for offshore artificial islands[J].Marine Geology & Quatrn-ary Geology, 2011,31(4):83-88.

[ 7 ] 丁勇春，李光辉，王建华. 海上人工岛内深基坑变形与稳定分析[J].岩土工程学报,2012,34(增刊1):519-524.

DING Yong-chun, LI Guang-hui, WANG Jian-hua. Deformation and stability of deep excavations in artificial offshore island[J]. Chinese Journal of Geotechnical Engineering, 2012,34(Supp1):519-524.

[ 8 ] 肖忠，王元战，及春宁,等. 波浪作用下加固软基上大圆筒结构稳定性分析[J].岩土力学, 2010,31(8): 2648-2654.

XIAO Zhong, WANG Yuan-zhan, JI Chun-ning, et al. Stability analysis of large cylindrical structure for strengthening soft foundation under wave load[J]. Rock and Soil Mechanics, 2010,31(8): 2648-2654.

[ 9 ] 郑颖人，叶海林，黄润秋,等. 边坡地震稳定性分析探讨[J].地震工程与工程振动,2010,30(2):173-180.

ZHENG Ying-ren, YE Hai-lin, HUANG Run-qiu, et al. Study on the seismic stability analysis of a slope[J].Journal of Earthquake Engineering and Engineering Vibration, 2010,30(2):173-180.

[10] 郑颖人，赵尚毅. 岩土工程极限分析有限元法及其应用[J]. 土木工程学报,2005,38(1):91-98.

ZHENG Ying-ren, ZHAO Shang-yi. Limit state finite element method for geotechnical engineering analysis and its aplications[J]. China Civil Engineering Journal, 2005, 38(1):91-98.

[11] Biot M A. General solution of the equation of elasticity and consolidation for a porous material [J]Journal of Applied Mechanics, 1956, 23: 91-96.

[12] Itasca Consulting Group Inc. Fast Lagrangian Analysis of Continua in 3 Dimensions[M]. Minneapolis: Itasca Consulting Group Inc,2002.

[13] Martin G R, Finn W D L,Seed H B. Fundamentals of liquefaction under cyclic loading[J]. Geotech., Div. ASCE, 1975,101(GT5):423-438.

[14] Byrne P. A cyclic shear-volume coupling and pore-pressure model for sand[J]. Geotechnical Earthquake Engineering and Soil Dynamics, 1991, 24(1):47-55.

[15] Hardin B O, Drnevich V P. Shear modulus and damping in soils: Ⅰ. Measurement and Parameter Effects, Ⅱ. Design Equations and Curves[R]. Technical Reports UKY 27-70-CE 2 and 3, College of Engineering, University of Kentucky, Lexington, Kentucky.

[16] 庄海洋.土-地下结构非线性动力相互作用及其大型振动台试验研究[D].南京：南京工业大学，2006.

Dynamic stability of an artificial island triggered by self weight, seepage and earthquake

LAIJie1,ZHENGYing-ren1,2,LIXiu-di1,LIUYun4(1. Department of Civil Engineering，Logistical Engineering University，Chongqing 401311，China；2. Chongqing Engineering and Technology Research Center of Geological Hazard Prevention and Treatment, Chongqing 400041, China；3. Chongqing Key Laboratory of Geomechanics & Geoenvironment Protection, Chongqing 401311, China;4. School of Civil Engineering，Chongqing Jiaotong University, Chongqing 400074, China)

Abstract:Because there are few papers published about dynamic stability of an artificial island under coupled actions of gravity, seepage, and earthquake, the strength reduction dynamic analysis method was introduced to study the dynamic stability of an artificial island. Its finite element model was built, the dynamic constitutive equations of Finn-Byrne and the modified Hardin-Drnevich were used for this artificial island under multi-field coupled actions. Its scope of liquefaction, stress distribution, and dynamic stability were analyzed. Calculation results showed that 1) this island can meet the requirement of dynamic stability under earthquake, because shear strength of muck layer is quite low, the final fracture surface is composed of the lower part of stones filled and mud layer under earthquake; 2) owing to precipitation, water seepage flows from outside to inside of the island, the effective stress and liquefaction resistance ability of soil increase in the outside of the island, however, those in inside of the island drop lower, so the soil in inside is more likely to be liquefied; 3) due to constraints of surrounding soils, soil local liquefaction doesn’t lead to high deformation, only more liquefied soil does. The results provided a reference for dynamic analysis of artificial islands.

Key words:artificial island; seepage; strength reduction dynamic analysis method; liquefaction

中图分类号:P315.72+6

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.05.028

通信作者郑颖人 男，中国工程院院士，博士生导师，1933年生

收稿日期：2015-06-29修改稿收到日期：2015-08-30

基金项目：国家重点研究发展计划(973)项目(2011CB013600)；国家自然科学基金(51378496;51178457;41272285)；重庆自然科学基金(CSTC2013JCYJYS0002)

第一作者 赖杰 男，博士生，1986年生