基于变尺度随机共振的冲击信号自适应提取与识别方法

曹衍龙， 杨毕玉， 杨将新， 郑仕谱， 周威杰(浙江大学 机械工程学系，杭州　310027)



基于变尺度随机共振的冲击信号自适应提取与识别方法

曹衍龙， 杨毕玉， 杨将新， 郑仕谱， 周威杰(浙江大学 机械工程学系，杭州310027)

摘要：针对不同设备故障会产生不同冲击信号类型的问题，为了克服传统指标不能区分冲击信号类型的不足，分析了冲击信号峭度值和近似熵的特性，将两个指标相结合，构造冲击信号特征系数，在此基础上提出了一种基于变尺度随机共振的冲击信号自适应提取与识别方法，实现强噪声环境中弱冲击信号的提取与识别。最后，通过仿真验证该方法的有效性和可行性。

关键词：冲击信号；变尺度随机共振；信号提取；信号识别

自1981年Beniz等[1]提出随机共振(SR)的概念之后，人们对随机共振进行了很多的研究，并利用其在强噪声下可以识别微弱信号的特性将其应用于信号处理领域。传统随机共振技术多应用于周期特征信号检测[2-4]，鲜有对于冲击信号的提取与识别处理。然而，在工程中存在大量非周期信号，微弱冲击信号是机电系统中一类常见的特征信号，往往包含重要的设备状态信息。比如核电站松动部件的跌落碰撞；利用突变信号进行桥梁等支撑结构的故障诊断。因此，冲击信号的提取与识别研究具有很强的工程实际意义。

文献[5-6]研究了随机共振的基本原理，在此基础上，实现了微弱冲击信号在有色背景噪声中的提取。文献[7-10] 分别从大参数条件下、测度指标的选择、结构参数搜索规则、随机共振系统本身等不同的侧重点出发，研究了周期冲击信号的检测提取。总的来说，现有的冲击信号随机共振检测方法起步较迟，相关文献很少。特别是针对冲击信号类型识别的文献目前还没有。基于上述情况，本文提出了一种基于随机共振的冲击信号自适应提取与识别方法，在提取出冲击信号的同时，也凸显出单冲击信号和振荡衰减冲击信号类型特征区别。

1单稳态随机共振模型

非线性双稳态系统的随机共振通常都是以系统输出在双势阱间的跃迁为特征的，也就说随机共振只有在双稳态阱间发生跃迁时才能产生。但是冲击信号不是周期信号，只在短时间内突变，随后又迅速返回初始值。所以冲击信号作用于双稳态系统时，很难在两个势阱间形成稳定的跃迁，其运动形式是粒子在单一势阱中运动或者发生一次跃迁后在另一个势阱中做单阱振荡。故本文不采用双稳态随机共振系统来实现信号的提取与识别。

冲击信号作为一种宽频短时瞬变信号，在随机共振中具有阱内共振的特点，对模型参数的合理选取表现出很高的敏感性。单稳态随机共振模型[11]中没有势垒，有且仅有一个稳态点，却依然表现出良好的“共振”特性，为冲击信号的提取提供了一个行之有效的解决途径。

由非线性朗之万方程所描述的单稳态随机共振系统提取模型为：

(1)

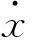
(2)

式中：a为模型参数，表示随机共振系统的偏置，影响模型稳态点的位置，取大于等于零的实数，即稳态点在x轴的右侧；b亦为模型参数，取大于零的实数。

2基于变尺度随机共振的自适应冲击信号提取方法

冲击信号在单稳态非周期随机共振系统中，模型参数对系统的稳定性具有很高的敏感度，参数选择的好坏直接影响系统输出的优劣，如何得到良好的参数，关键是确定良好的测度指标。

2.1冲击信号特征系数的构造

2.1.1峭度指标

峭度指标K对信号中冲击成分非常敏感，常被用作振动信号的时域参数指标，例如故障诊断中被用于实现对损伤的识别。K是反映信号分布特性的数值统计量，定义为信号四阶矩与二阶矩平方的比值[12]：

(3)

式(3)中，x={x1,x2, …,xN}T为信号序列，N为信号长度。设

(4)

式中：

(5)

(6)

(7)

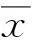
2.1.2近似熵[13-14]

近似熵是用一个非负数来表示某一时间序列的复杂性，越复杂的时间序列对应的近似熵越大。因此近似熵能表征信号的复杂性，用于识别冲击信号的类型。

设系统输出序列{x(t),i=1, 2, 3, …,N}，预先赋值模式维数m和相似容限r，则近似熵的计算步骤如下所示：

1) 将输出序列{x(i),i=1, 2, 3, …,N}按顺序组成m维矢量X(i)：

X(i)=[x(i),x(i+1),…,x(i+m-1)],

i=1～N-m+1

(8)

2) 计算矢量X(i)与X(i)其他各矢量X(j)之间的距离(j=1～N-m+1,j≠i):

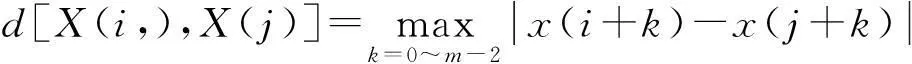
(9)

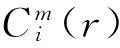
(10)

(11)

5) 对m+1重复(1)～(4)步骤，得到φm+1(r)。

6)序列{x(t),i=1,2,3,...,N}的近似熵估计值为：

ApEn(m,r)=φm(r)-φm+2(r)

(12)

可见近似熵的值与参数m和r有关，根据经验，通常取m=2,r=0.1～0.25SD(x)，其中SD(x)表示序列{x(i),i=1,2,3,…,N}的标准差，根据本文研究对象特性，取m=2,r=0.25SD(x)。

2.1.3冲击信号特征系数构造

当输入信号为单冲击信号时，经过随机共振处理后，输出信号有且仅有一个冲击。输出效果越好，峭度指标K越大，近似熵ApEn的值近乎不变。当输入信号为振荡衰减冲击信号时，经过随机共振处理后，此时输出信号可以有多个冲击。以最大化K作为检测冲击信号的指标，输出只有一个冲击，这是系统只针对振荡衰减冲击信号中幅值最大的冲击进行的检测。这势必造成了两种冲击信号的混淆，难以区分信号类型。通过K和ApEn的数学模型计算以及实验数据的验证，当系统输出由一个冲击增加到两个冲击时，ApEn的增大比例值明显高于K的减小比例值。故结合K和ApEn的指标优势构造冲击信号特征系数KA，定义为：

KA=K*ApEn

(13)

式中，K为峭度指标，ApEn为近似熵。

由上述分析可知，通过式(13)的最大化准则，当输入信号为单冲击信号时，输出信号仅有一个单冲击。当输入信号为震荡衰减冲击信号时，输出信号有多个冲击，由此可以自适应地确定输入信号的类型。

2.2基于变尺度SR的冲击信号自适应提取的实现

为了克服传统随机共振只能检测小参数信号的限制问题，引入变尺度随机共振以扩大应用范围。变尺度随机共振是一种检测大参数信号的随机共振方法。其原理是，改变计算步长h，即h不取采样频率的倒数，而令h>1/fs，经验范围为0.1到1。通过改变系统结构参数a,b和计算步长h，即可检测出大参数的信号。

基于冲击特征系数KA的自适应随机共振冲击信号提取模型流程图，见图1。

图1　自适应随机共振冲击信号提取与识别方法流程图Fig.1 Flow diagram of impact signal extraction

基于KA的自适应随机共振的实现过程为：

1) 初始化KAmax=0，设置系统参数a,b和h的初值，确定搜索范围和搜索步长，本文将a,b,h的搜索范围分别设置为[0,10]、[0,10]、[0.1,1]，搜索步长设置为0.1；

2) 利用龙格库塔算法对当前参数所对应的系统进行仿真，获得系统的输出信号，计算输出信号的KA值；

3) 判断KA是否大于KAmax。如果是，则更新KAmax，取KAmax=KA，同时令aopt=a,bopt=b,hopt=h，然后再按设定步长更新a,b,h。如果否，直接按设定步长更新a,b,h；

4) 判断a,b,h是否搜索完毕，如果是，最终得到最优参数为aopt,bopt,hopt，如果否，返回第二步继续循环。

5) 获得最优参数，实现最佳输出。

其中KA所计算的序列，应该排除初始零点附近的值。因为冲击信号是在单势阱中完成运动的，输出序列必将在初始零点附近有突变，从而进入某一势阱的最低点。

3仿真试验

为了验证提出的冲击信号检测与识别方法的有效性，本文采用两种冲击信号的数学模型。其中单冲击信号由下列模型产生：

(14)

式中,h0为冲击的峰值高度，W为冲击的半峰宽，t0表示信号的起始时间位置。令参数h0=0.5,W=0.1 s,t0=3.3 s，此时原始单冲击信号如图2(a)所示。图2(b)为叠加噪声后的混合输入信号，通过自适应随机共振系统后，如图2(c)所示，得到最优输出。此时不同噪声强度下的模型参数a、b和h，冲击特征系数KA如表1所示。由图2可知在噪声强度D小于3时，该提取模型能很好地提取出单冲击信号。当噪声强度D值等于3时，可以看到输出波形图存在噪声干扰，但此时并不突出。当噪声强度D值等于4时，模型输出淹没于噪声中，难以区分开来。

表1　不同噪声强度下单冲击信号

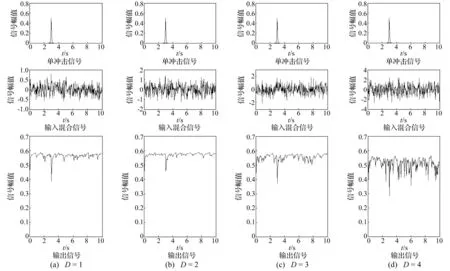
图2　单冲击信号输出图Fig.2 Single signal impact output

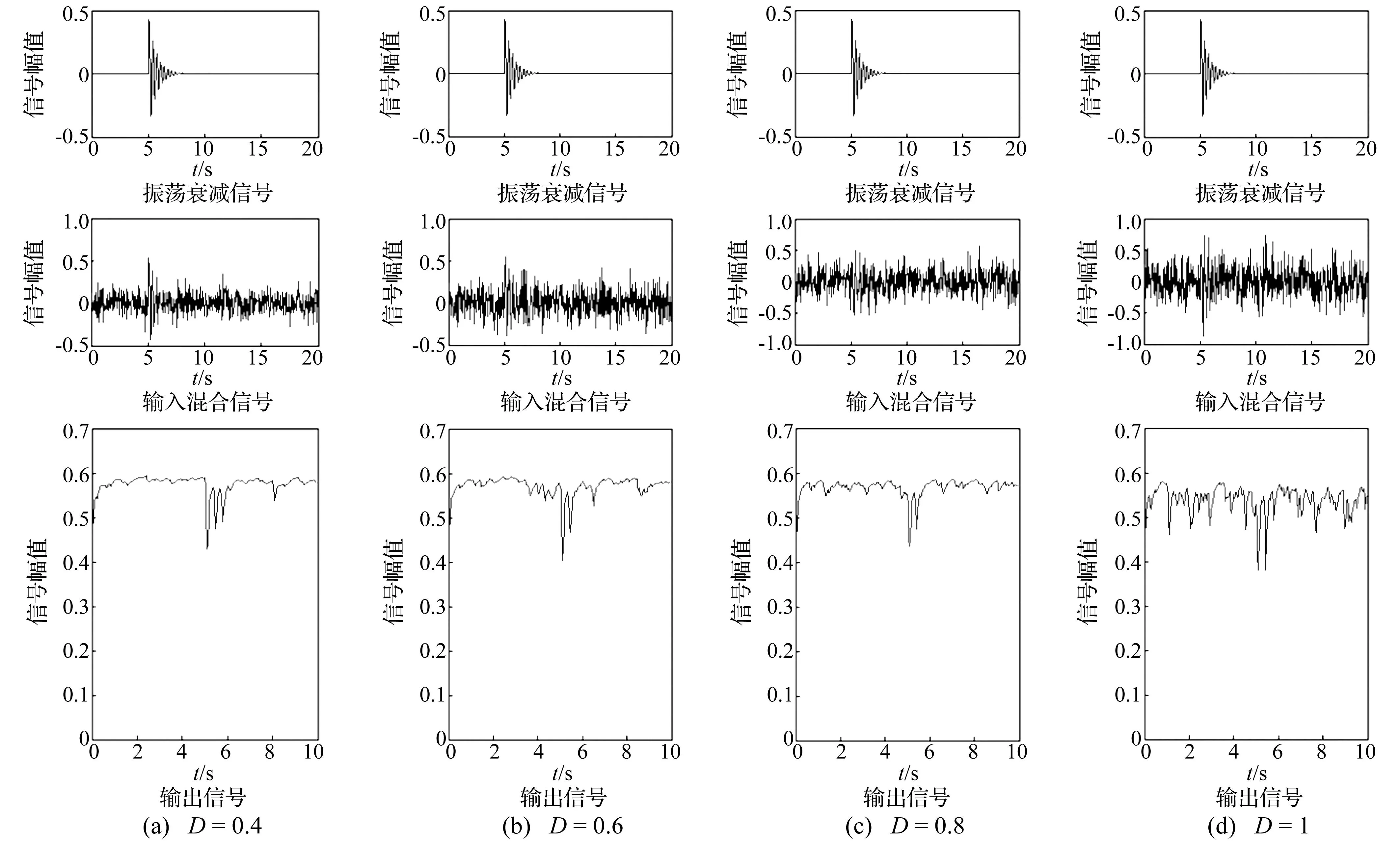
图3　振荡衰减冲击信号输出图Fig.3 Dampening impact signal output

振荡衰减冲击信号由下列模型产生：

(15)

式中,A为冲击幅值，k为冲击衰减系数，f为振荡频率。

令参数A=0.5,k=0.5,f=5 Hz，此时原始振荡衰减冲击信号如图3(a)所示。图3(b)为叠加噪声后的混合输入信号，通过自适应随机共振系统后，如图3(c)所示，得到最优输出，此时各信噪比下的模型参数a、b和h，冲击特征系数KA如表2所示。由图3可知，在噪声强度D小于1时，该模型能很好地提取出振荡衰减冲击信号。当噪声强度D值等于1时，模型去噪能力下降，勉强可以从输出信号中提取出振荡冲击信号。当噪声强度D值超出1时，噪声主导了共振效果，难以识别信号的存在与否。由上可知，相比单冲击信号的提取，振荡衰减信号难以在较大噪声强度下实现提取。

从图2和图3输出信号可以看出，系统达到随机共振状态，输出与原始冲击信号出现的时间和特征达到很好地一致。信号只是在单一势阱中运动，而没有发生两个势阱间的跃迁。这既验证了SR能检测冲击信号，也表明了SR单势阱内运动模型来检测冲击信号效果更佳。同时根据输出的冲击个数，很容易的区分开故障冲击信号的类型。

表2　不同噪声强度下震荡衰减信号

4结论

针对强噪声背景是冲击信号的提取问题，利用峭度指标和近似熵的数学特性，构造了冲击信号特征系数，提出冲击信号的提取方法，经仿真验证无论是单冲击信号，还是振荡衰减冲击信号，均有不错的输出效果。同时在一定程度上识别冲击信号类型，便于后期针对设备故障冲击信号类型的诊断。

参 考 文 献

[ 1 ] Benzi R, Sutera A, Vulpiani A. The mechanism of stochastic resonance[J]. Journal of Physics A: Matb-ematical and General, 1981, 14: 453-457.

[ 2 ] 杨定新,胡茑庆. 基于随机共振电路模拟的微弱周期信号检测[J]. 电路与系统学报, 2004, 9(6): 135-138.

YANG Ding-xin, HU Niao-qing. Detecting weak signal based on analog simulating of stochastic resonance[J]. Journal of Circuits and Systems, 2004,9(6): 135-138.

[ 3 ] 李强,王太勇,冷勇刚,等. 基于变步长随机共振的弱信号检测技术[J]. 天津大学学报, 2006,39(4): 432-437.

LI Qiang, WANG Tai-yong, LENG Yong-gang, et al. Weak signal detection based on step-changed stochastic resonance[J]. Journal of Tianjin University, 2006,39(4): 432-437.

[ 4 ] 夏均忠,刘远宏，马宗坡,等. 基于调制随机共振的微弱信号检测研究[J]. 振动与冲击, 2012,31(3): 132-135.

XIA Jun-zhong, LIU Yuan-hong, MA Zong-po, et al. Weak signal detection based on the modulated stochastic resonance[J]. Journal of Vibration and Shock, 2012,31(3): 132-135.

[ 5 ] 高雯. 基于非线性动力学原理的弱信号检测理论及提取方法研究[D]. 北京:北京邮电大学, 2009.

[ 6 ] 王强. 基于随机共振的微弱冲击信号检测技术研究[D]. 北京:北京邮电大学, 2010.

[ 7 ] 范胜波,王太勇,冷勇刚,等.基于变尺度随机共振的弱周期性冲击信号的检测[J].中国机械工程, 2006,17(4):387-390.

FAN Sheng-bo, WANG Tai-yong, LENG Yong-gang, et al. Detection of weak periodic impact signals based on scale transformation stochastic resonance[J]. China Mechanical Engineering, 2006,17(4):387-390.

[ 8 ] 谭继勇,陈雪峰,何正嘉. 冲击信号的随机共振自适应检测方法[J]. 机械工程学报,2010, 46(23): 61-67.

TAN Ji-yong, CHEN Xue-feng, HE Zheng-jia. Impact signal detection method with adeptive stochastic resonance[J]. Journal of Mechanical Engineering,2010,46(23): 61-67.

[ 9 ] 李继猛,陈雪峰,何正嘉. 采用粒子群算法的冲击信号自适应单稳态随机共振检测方法[J]. 机械工程学报,2011, 47(21): 58-63.

LI Ji-meng, CHEN Xue-feng, HE Zheng-jia. Adaltive monostable stochastic resonance based on PSO with applicationin impact signal detection[J]. Journal of Mechanical Engineering, 2006,17(4):387-390.

[10] 石鹏,冷永刚,范胜波,等. 双稳系统处理微弱冲击信号的研究[J]. 振动与冲击, 2010,31(6): 150-154.

SHI Peng, LENG Yong-gang, FAN Sheng-bo, et al. A bistable system for detecting a weak pulse signal[J]. Journal of Vibration and Shock, 2010,31(6): 150-154.

[11] Dybiec B, Lévy noises: Double stochastic resonance in a single-well potential[J]. Physical Review E80, 2009(041111): 1-7.

[12] Li Hua-feng, Bao Rong-tao, Xu Bo-hou. Intrawell stochastic resonance of bistable system[J]. Journal of Sound and Vibration, 2004:155-167.

[13] 胥永刚,李凌均,何正嘉. 近似熵及其在机械设备故障诊断中的应用[J]. 信息与控制, 2002,31(6): 547-551.

XU Yong-gang, LI Ling-jun, HE Zheng-jia. Approximate entropy and its applications in mechanical fault diagnosis[J]. Information and Control, 2002,31(6): 547-551.

[14] 王步宇,俞亚楠. 移动荷载作用下结构损伤的近似熵分析[J]. 振动与冲击, 2010,29(6): 125-128.

WANG Bu-yu, YU Ya-nan.Approximate entropy analysis of structural damage under moving load[J]. Journal of Vibration and Shock, 2010,29(6): 125-128.

Impact signal adaptive extraction and recognition based on a scale transformation stochastic resonance system

CAOYan-long,YANGBi-yu,YANGJiang-xin,ZHENGShi-pu,ZHOUWei-jie(Department of Mechanical Engineering, Zhejiang University, Hangzhou 310027, China)

Abstract:Different equipments’ faults produce different types of impact signal. But the traditional index can’t distinguish the types of impact signal. In order to overcome this shortcoming, here, the kurtosis value and approximate entropy of impact signals were analyzed, the impact signal characteristic coefficient was constructed combining these two indexes. Afterward, a method of impact signal adaptive extraction and recognition based on a scale transformation stochastic resonance system was presented. Then the extraction and recognition of weak signals under a strong noise environment was realized. Finally, the effectiveness and feasibility of the method were verified through simulation.

Key words:impact signal; scale transformation stochastic resonance; signal extraction; signal recognition

中图分类号:TH911.4

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.05.010

收稿日期：2014-07-04修改稿收到日期：2015-03-25

基金项目：国家自然科学基金(51175466;51575486)资助项目

第一作者 曹衍龙 男，博士，教授，1975年11月生