具有形状记忆合金弹簧支承的转子系统的动力稳定性研究

任勇生， 杜成刚， 刘养航(山东科技大学 机械电子工程学院，山东 青岛　266590)



具有形状记忆合金弹簧支承的转子系统的动力稳定性研究

任勇生， 杜成刚， 刘养航(山东科技大学 机械电子工程学院，山东 青岛266590)

摘要：提出一个具有形状记忆合金(SMA)弹簧支承的旋转轴转子系统的自由振动分析模型。基于Euler-Bernoulli梁理论建立旋转轴的连续分布弹性振动方程， 并且考虑旋转轴材料内阻的影响。采用Brinson模型分析SMA螺旋弹簧的受限回复刚度特性。在振型假设的基础上利用虚功原理得到转子系统的特征方程。通过数值计算分析了SMA弹簧的激励温度和初始应变对转子系统的临界转速和失稳阈的影响规律。研究表明， 利用SMA弹簧的受限回复特性调节支承刚度可以提高转子系统的临界转速和失稳阈，从而增强转子系统的动力学稳定性。

关键词：形状记忆合金弹簧; 弹性支承; 转子; 稳定性

提高转子的临界转速、降低转子通过临界转速的振幅以及超临界状态运行下转子的稳定性，一直是转子动力学领域十分关注的问题。智能材料与结构理论与技术领域的发展，为转子系统的振动主动控制，提供了一个新的有效的途径[1]。形状记忆合金(SMA)是一种可以广泛应用于结构振动控制的智能材料，近年来，利用SMA改善振动系统的动力学性能，实现振动控制的研究，已经取得了一些进展[2]。SMA用于转子振动控制，可采用两种结构形式，一种是将SMA丝直接埋入转子中，另一种是利用SMA弹簧支承转子。文献[3-7]研究埋入SMA丝的转子系统, 在激活SMA情况下的刚度特性以及动力学行为。He等[8]提出一个具有SMA偏置弹簧支承的转子-轴承系统的二自由度动力吸振器模型，借助于改变SMA偏置弹簧的刚度控制转子通过临界转速的共振响应。Santos等[9]以及Sitnikova等[10]对具有普通弹性支承和SMA弹簧支承的单自由度转子动力学系统的动力学响应进行了比较研究，发现利用SMA弹簧的耗散特性可以改变系统的动力学特性。Silva等[11]分析了二自由度Jeffcott转子-轴承系统的不平衡受迫振动响应行为，模型采用SMA支承以及转子和轴承之间的间隙非光滑特性。结果表明，SMA支承的迟滞耗散特性以及温度依赖特性能够适用于转子系统的被动和自适应主动振动控制。然而，目前利用SMA弹簧支承改善转子系统动力学特性的研究中的转子仅限于单自由度或者二自由度离散模型；现有的文献大多只涉及对转子系统通过临界转速共振响应的研究，没有考虑SMA弹簧支承对转子系统动力学稳定性的影响。此外，为了更加准确地预测SMA弹簧的作动特性，采用精细的本构模型描述SMA的力学行为也是十分必要的。

本文研究具有SMA弹簧支承的弹性旋转轴的自由振动与稳定性。旋转轴采用Euler-Bernoulli梁理论进行结构建模，并且计入材料的内阻。基于Brinson模型[12]描述SMA弹簧的受限回复刚度特性。在建立旋转轴-SMA弹簧支承系统自由振动方程的基础上，采用特征值解法得到转子系统的固有频率和阻尼。通过数值分析揭示了SMA弹簧支承对转子系统的临界转速和失稳阈的影响规律。

1转子系统数学模型

1.1具有SMA弹簧支承的旋转轴转子系统自由振动方程

图1　位于SMA弹簧上的弹性轴Fig.1 Elastic shaft mounted on SMA spings

C相对惯性坐标系的位移为

(1)

弹性轴的位移边界条件为

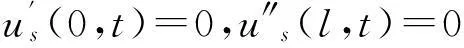
us(0,t)=0,us(l,t)=0

(2)

式中，( )′和( )″分别表示对x的一阶和二阶偏导数。

旋转坐标系下考虑材料内阻轴的自由振动方程为[13]

∀x∈[0,l]

(3)

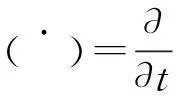
根据边界条件可以得到两个补充方程如下

(4)

(5)

假定轴的弹性位移以及刚体位移和转角分别表示为

(6)

式中，Usn，Ubn为复位移，θbn是复转角，λn是复特征值。

利用虚功原理，方程(3)变为[13]：

(7)

虚位移取

(8)

将式(8)和式(6)代入方程(7)、(4)和(5)，化简得

(9)

式中

(10)

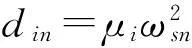
由特征方程(9)解出的特征值可以表示为

λn=ωn+idn

(11)

式中，实部ωn表示角频率，虚部dn表示模态阻尼。

1.2SMA螺旋弹簧的刚度

线弹性螺旋弹簧的最大切应力为[14]

(12)

式中，K表示Wahl修正因子，F是外力，R表示弹簧半径，r表示弹簧丝半径。假设K取单位1。

线弹性螺旋弹簧的转角可通过分析微元变形求出，如图2所示。

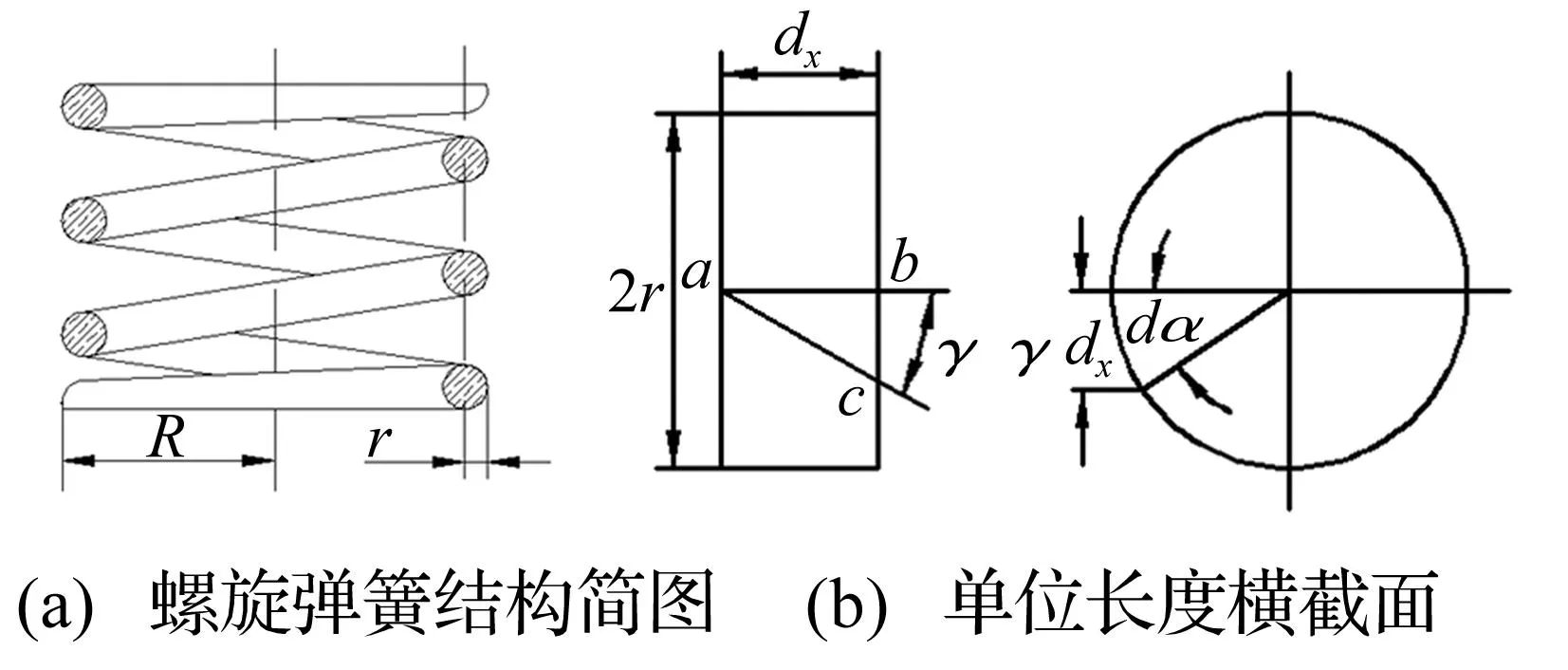
图2　螺旋弹簧结构简图(a)与单位长度横截面(b)Fig.2 SMA helical spring (a) and its cross-section element (b)

取弹簧丝微元表面的平行于弹簧轴的直线ab，ab在变形后偏转角度γ，转到ac的位置。根据虎克扭转定律，γ可以表示为

(13)

弹簧截面偏转角

(14)

其中，N是总有效圈数。

弹簧总变形为

(15)

弹簧的刚度系数由方程(15)可得如下

(16)

剪切模量的表示式为

(17)

基于描述SMA本构关系的Brinson模型[12]，可以建立SMA在完全受限回复状态下的杨氏模量与马氏体相变百分数之间的关系E(ξ)=EA+ξ(EM-EA)，进而可以分析杨氏模量随温度变化的规律。SMA弹簧的初始状态为T0=20°C，σ0=122.43 MPa，ε0=0.5%，ξs0=0.6，ξT0=0，材料常数aM、bM、aA和bA可以用表1中的参数计算出来。取SMA弹簧丝的半径为r=0.02 m，弹簧半径为R=0.05 m，有效圈数N=2。计算出SMA螺旋弹簧的刚度在升温阶段随温度变化的曲线，如图3所示，对应的初始应变取ε0=0.005。图中的Km为处于低温马氏体相的弹簧常数，通过计算得Km=2.62×106Nm-1。

2数值结果与讨论

本文算例中旋转轴以及轴承的材料和几何参数选取如下[13]：E=2.08×1011Pa，ρ=7 830 kg/m3，l=1.27 m，r=0.050 8 m，ke=1.751 2×107Nm-1，μi=0.000 2 s，SMA螺旋弹簧材料和几何的基本参数的取值与上节算例相同。

表1　SMA材料常数

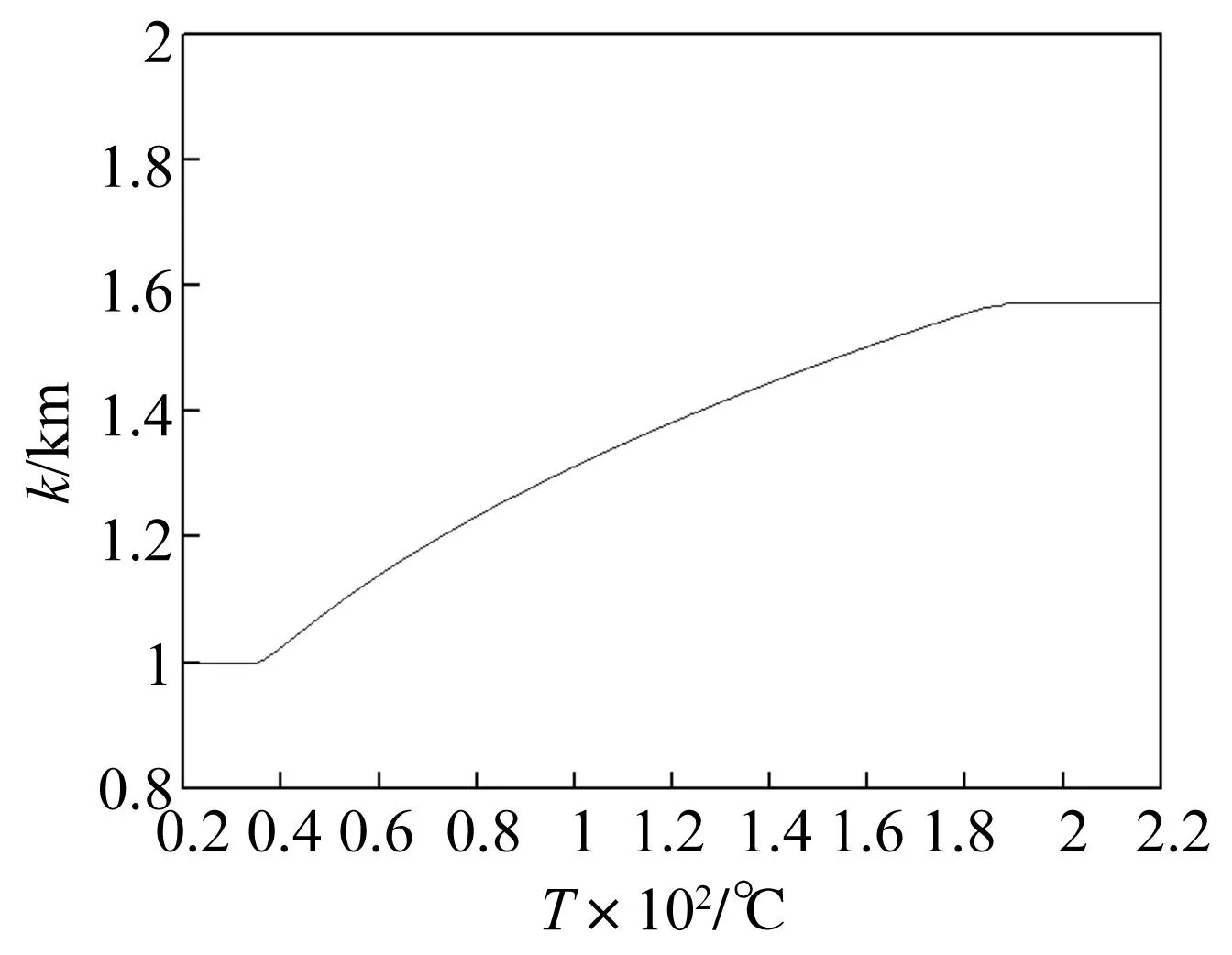
图3　SMA弹簧刚度与温度的关系Fig.3 The relation of spring stiffness of an SMA spring and temperature

取SMA的激活温度T=80 ℃，初始应变ε0=0.01，得到具有普通弹簧支承的旋转轴转子系统与具有SMA弹簧支承的旋转轴转子系统的坎贝尔图和对数衰减率曲线，结果分别如图4和图5所示。 图中的nF-，nB-，nB+，nF+，(n=1，2)分别表示转子系统前两阶模态对应的4个涡动频率和对数衰减率，“F”表示正进动，“B”表示反进动。

由图4可以看出，与具有普通支承的转子系统相比，具有SMA弹簧支承的转子系统的涡动频率有明显的提高，因而有效地增加了系统的临界转速。

对比图5具有两种支承转子系统的计算结果，可以看出，具有SMA弹簧支承的转子系统的对数衰减率-转速曲线与Ω轴的交点位置，向更高转速的一侧移动，这表明具有SMA弹簧支承转子系统的失稳阈值也相对更高。

图6和图7分别表示温度的变化对第一阶涡动频率和衰减率的影响。由此可以看出，系统的涡动频率随着温度的增加而增加，对应于1F-，1B-分支的衰减率-转速曲线与Ω轴的交点的位置，随着温度的增加会向着高转速一侧移动，表明温度的增加会使得失稳阈增加。图8～9分别表示初始应变的变化对第一阶涡动频率和衰减率的影响。由图可见，相对于温度而言，初始应变的变化对涡动频率和衰减率的影响似乎并不十分明显。

图4 两种支承转子系统的坎贝尔图Fig.4Campbelldiagramofashaftsupportedoftwotypessupports图5 两种支承转子系统的正进动对数衰减率与转速的关系Fig.5Thelogarithmicdecrementintheforwardwhirlspeedoftwotypessupports图6 温度对第一阶涡动频率的影响Fig.6Effectoftemperatureonthefirstwhirlfrequcency

图7 温度对第一阶衰减率的影响Fig.7Effectoftemperatureonthefirstlogarithmicdecrement图8 初始应变对第一阶涡动频率的影响Fig.8Effectofinitialstrainonthefirstwhirlfrequcency图9 初始应变对第一阶衰减率的影响Fig.9Effectofinitialstrainonthefirstlogarithmicdecrement

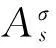
图10　第一阶临界转速随温度变化曲线(临界速度Ωcr)Fig.10 The variation of the first critical speed with temperature

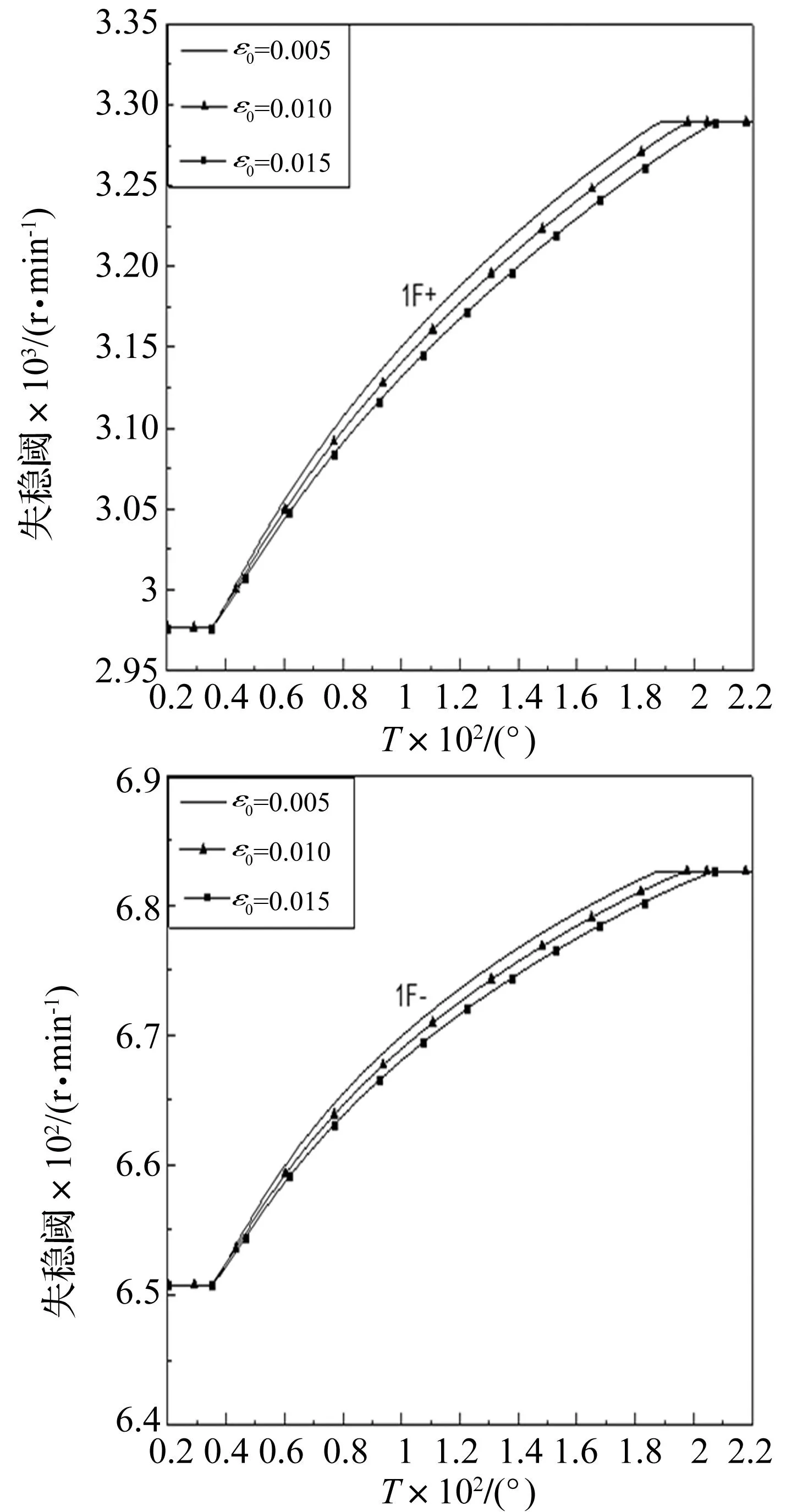
图11　第一阶失稳阈随温度变化曲线Fig.11 The variation of the first instability threshold with temperature

3结论

研究了具有SMA弹簧支承的旋转轴-轴承转子系统的振动稳定性。基于Euler-Bernoulli梁模型建立旋转轴连续分布振动模型，并且考虑轴的材料内阻的影响。SMA弹簧的受限回复刚度特性借助于Brinson模型进行计算。通过数值求解转子系统的特征值问题得到涡动频率和衰减率。揭示了SMA弹簧支承对转子系统的临界转速和失稳阈的影响规律。研究表明：

(1) 采用SMA弹簧支承能够明显改善转子系统的动力稳定性。

(2) 在SMA马氏体转变阶段，转子系统的临界转速和失稳阈值随着相变激励温度的增加而显著提高。

(3) 增加SMA初始应变将会导致转子系统的临界转速和失稳阈的降低。但是，相对于SMA激励温度参数而言，SMA初始应变对转子系统涡动频率和衰减率的影响不够明显。

参 考 文 献

[ 1 ] 孟光.转子动力学研究的回顾与展望[J].振动工程学报,2002,15(1):1-9.

MENG Guang. Retrospect and prospect to the research on rotordynamics[J].Journal of Vibration Engineering,2002,15(1):1-9.

[ 2 ] 任勇生, 王世文, 李俊宝, 等. 形状记忆合金在结构主被动控制中的应用[J]. 力学进展, 1999, 29(1): 19-33.

REN Yong-sheng, WANG Shi-wen, LI Jun-bao,et al. Shape memory alloy and it’s application in active and passive vibration control[J].Advances in mechanics,1999,29(1):19-33.

[ 3 ] Baz A, Chen T. Performance of nitinol reinforced drive shafts[C]//In Smart Structure and Intelligent Systems, SPIE 1917, 1993, 791.

[ 4 ] Tylikowski A, Hetnarski R B. Semiactive control of a shape memory alloy hybrid composite rotating shaft[J].International Journal of Solids and Structures,2001,38:9347-9357.

[ 5 ] Gupta K. Critical speed analysis of fibre-reinforced composite rotor embedded with shape memory alloy wires[J]. Int. J. Rotat. Mach., 2000, 6 (3):201-213.

[ 6 ] Sawhney S, Jain S K. Vibration control of fibre-reinforced composite rotor using shape memory alloy (SMA) wires[D]. IT Delhi, 2001, New Delhi. BTech Dissertation.

[ 7 ] 任勇生，赵仰生，安瑞君，等. 具有形状记忆合金丝的复合材料轴转子系统的振动与稳定性[J].振动与冲击，2015，34(3):136-143.

REN Yong-sheng,ZHAO Yang-sheng,AN Rui-jun, et al. Vibration and stability of SMA wires composite shaft-rotor systems[J]. Journal of Vibration and Shock, 2015, 34(3): 136-143.

[ 8 ] He Yong-yong, Oi S, Chu Fu-lei,et al. Vibration control of a rotor-bearing system using shape memory alloy: I.Theory[J]. Smart Mater. Struct., 2007,16:114-121.

[ 9 ] Santos B C, Savi M A. Nonlinear dynamics of a nonsmooth shape memory alloy oscillator[J].Chaos, Solitons and Fractals, 2009, 40 (1):197-209.

[10] Sitnikova E, Pavlovskaia E, Wiercigroch M, et al. Vibration reduction of the impact system by an SMA restraint: numerical analysis[J].International Journal of Nonlinear Mechanics,2010,45 (9):837-849.

[11] Silva L C, Savi M A, Paiva A. Nonlinear dynamics of a rotordynamic nonsmooth shape memory alloy system[J]. Journal of Sound and Vibration,2013, 332:608-621.

[12] Brinson L C. One-dimensional constitutive behavior of shape memory alloys: Thermomechanical derivation with non-constant material functions and redefined martensite internal variable [J]. Journal of Intelligent Material Systems and Structures, 1993, (4): 229-242.

[13] Montagnier O, Hochard C. Dynamic instability of supercritical driveshafts mounted on dissipative supports-Effects of viscous and hysteretic internal damping[J]. Journal of Sound and Vibration, 2007, 305:378-400.

[14] Shigley J E. Mechanical Engineering Design[M]. New York: McGraw-Hill, Inc, 1977.

Dynamic stability of a rotor-bearing system with shape memory alloy support

RENYong-sheng,DUCheng-gang,LIUYang-hang(College of Mechanical and Electronic Engineering, Shandong University of Science and Technology, Qindao 266590, China)

Abstract:The dynamic model of a rotor-bearing system with shape memory alloy (SMA) support was proposed. Euler-Bernoulli beam theory was used to derive its continuous elastic vibration equations. Internal viscous damping of the shaft was also included in equations. Brinson constitutive model was adopted to describe the stiffness charateristic of SMA helical spring under restrained strain. On the basis of assumed modal shapes, the eigen-equation of the rotor system was obtained by using the virtural work principle. The influcences of excitation temperature and initial strain of SMA helical spring on the critical speed and instability threshold of the rotor system were analyzed with numerical simulation. Results showed that the support siffness adjustment based on the restrained recovery of SMA helical spring can significantly improve the critical speed and instability threshold of the rotor system to enhance its dynamic stability.

Key words:shape memory alloy spring; elastic support; rotor; stability

中图分类号:TH132

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.05.011

收稿日期：2015-07-06修改稿收到日期：2015-09-23

基金项目：国家自然科学基金(11272190);山东科技大学研究生科技创新基金项目(YC150325)

第一作者 任勇生 男，博士，教授，1956年7月生