多普勒畸变声学信号的伪时频分析及其校正

张海滨， 陆思良， 何清波， 孔凡让(中国科学技术大学 精密机械与精密仪器系, 合肥　230027)



多普勒畸变声学信号的伪时频分析及其校正

张海滨， 陆思良， 何清波， 孔凡让(中国科学技术大学 精密机械与精密仪器系, 合肥230027)

摘要：位于运动轨迹旁的麦克风采集的运动声源信号存在多普勒畸变现象，这增加了信号分析的难度，特别对于高速列车道旁声学故障诊断工作。为了提高诊断的准确性和可靠性，提出了一种新的基于摩尔斯声学理论的多普勒信号伪时频分析，该分析给出了一种伪时频分布，对信号的时间中心和特征频率进行了有效估计，得到的参数用于信号重采样以校正其多普勒畸变，校正信号中能有效提取出信号中包含的故障信息。仿真信号和实验信号的分析结果表明，该方法能够用于提取多普勒畸变信号的参数，并加以校正，在道旁声学故障诊断中有较好的应用前景。

关键词：故障诊断;多普勒畸变;声学信号;伪时频分析

对于传统机械设备来说，由于轴承故障在所有的故障种类中占有的支配地位，因而其状态监测和故障诊断是必不可少的研究工作[1]。随着现代铁路运输的快速发展和不断提速，其安全性问题变得日益突出。美国的一项统计表明，列车轴承故障作为列车故障的主要类型，每年大约有50起跟其相关的列车出轨事故发生[2-3]。因此，加强轴承的监测和诊断，及时了解和掌握轴承的工作状态，可以尽量发挥轴承的工作潜力，避免或减少事故的发生，对列车的安全运行具有十分重要的意义。

早在20世纪80年代，列车声音检测系统(Acoustic Defective Bearing Detector,ADBD)技术的发展在预报和诊断轴承失效和过热方面就取得良好的效果[3]。作为一种非接触测量凡事，该系统采用轨边监测麦克风来获取轴承运行时发出的声音，可以发现轴承早期故障，具有成本低、普适性强等特点；但也因为一些技术难点的存在导致故障不能检测而引起的灾难性后果[4]。在诸多问题中，麦克风放置位置与铁轨的垂直距离以及轴承声源移动相对麦克风的横向速度，导致所采集得到的信号会存在不同于雷达、通讯等领域多普勒效应的畸变，因此对其进行分析和校正是进行精确的轴承故障信号特征提取和诊断的前提[5-8]。

在对该类声学多普勒畸变信号进行校正的研究中，Dybala[5, 9]首先提出了一种基于希尔伯特变换的面向干扰的动态信号重采样方法以消除道旁监测系统受到的多普勒效应的影响，然而这种方法在频域处理时只能包含单一的频率谱线，在特征频率分布比较密集的情况下难以进行有效的带通滤波，而且此时采用的希尔伯特变换的端点效应也对此方法的有效性产生不利的影响；文献[6]结合了重采样多普勒校正和整体平均经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)技术，但是并没有给出明确的多普勒参数估计方法，研究中默认信号的相关固有参数已知，因而在实际应用中受到限制；张翱等[7]提出了一种基于能量重心法的多普勒畸变信号校正方法，该方法是通过信号时频域的能量重心来进行瞬时频率估计，以及文献[8]所采用的时频脊线提取方法来估计多普勒参数，该类方法在时频域中如果有偶然高能频率分量的进入，将导致方法很难提出有效的瞬时频率分布，而且当信号处于较低的信噪比时，噪声的随机分布会给瞬时频率提取带来困难，所得到的参数精度也受到严重影响。

为了使多普勒畸变信号的参数提取有更强的适应性和对噪声的不敏感性，考虑到噪声能量的随机分布特点，本文提出一种基于信号能量积分原理的伪时频分析(FTFA)，该方法通过一种降维的多普勒小波变换(Dimension Reduction Dopplerlet Transform,DRDT)[10-11]，得到适用于多普勒畸变信号的伪时频分布(FTFD)；通过信号的FTFD，进而得到多普勒信号的两个基本参数：时间中心和特征频率；随后利用这两个参数通过时域重采样技术对信号的多普勒畸变进行校正并进行后期的相关诊断分析。最后本文通过对仿真信号及列车轴承内外圈故障实际声信号的分析处理，验证了该方法对道旁声学故障诊断工作的有效性。

1相关理论模型和原理分析

1.1道旁声学诊断模型

列车道旁声学故障诊断模型如图1所示，被测列车轴承声源从t=0时刻开始出发，相对于空气介质以速度v沿图中所示方向运动，在运动过程中其辐射出的声音信号经过一段传播距离后到达麦克风处。图中初始位置到麦克风的水平距离为S，t时刻轴承与麦克风的距离为R(t)，列车前进方向和轴承麦克风连线间的夹角θ(t)，麦克风和列车前进方向垂直距离为r。在列车速度为亚声速的情况下，考虑列车轴承声源为单极子点声源，并且传播介质为理想流体，即不存在黏滞性，没有能量损耗，声源的波动方程由简谐波q(t)=q0sinω0t给出，则根据摩尔斯声学理论[12]，可以得到t时刻麦克风采集到的轴承所发出的声压方程P(t)可由式(1)表示：

(1)

(2)

式中，t0即表示多普勒信号的时间中心，且有S=vt0。由该式可以看出，麦克风接收到的声音信号频率对相对于原信号频率(f0)呈现非线性畸变，本文所提出的方法即针对这种多普勒畸变信号进行校正分析。

图1　列车道旁轴承声学故障诊断模型Fig.1 Model of wayside train bearing fault diagnosis

1.2降维多普勒小波变换(DRDT)

多普勒小波变换是由邹红星等[10]为克服时频关系为线性的基函数的不足所提出的时频信号表示——Dopplerlet变换。该变换实质上是对信号的时频能量分布进行非线性分割，而以线性分割为特征的Fourier变换、短时Fourier变换、小波变换等均是其在参数取特定值时的特例。但是在已有的Dopplerlet变换中，忽略了多普勒变换中的幅值调制和观察者得到信号的时间延迟，而且在变换中需要六个参数来描述多普勒小波，这些参数很多时候并不必要，因而本文提出了一种降维的多普勒小波变换(DRDT)，将未知量从6降到2个，从而得到一个多普勒信号的新分布。考虑式(1)的幅值调制，提出新的多普勒小波：

(3)

在列车道旁声学故障诊断的实际应用中，瞬时频率f(t)由列车速度v、垂直距离r、原始频率f0和时间中心t0(S=vt0)所共同决定。但是实际上，参数v和r都可以通过其他手段准确测量或者获得，所以这里将其视为已知量。新的多普勒小波DRDt0,f0(t)将只由f0和t0所决定，因而可以将一个平方可积的信号s(t)∈L2(R)的DRDT表示为：

(4)

式(4)即为本文所定义的DRDT，和傅里叶变换类似，只是引入了一个新的时间中心数t0，这两个参数将给接下来的畸变校正过程中多普勒参数估计带来极大的便利和可能。

1.3重采样校正多普勒畸变的原理

信号频率畸变的还原通常使用重采样方法，而建立一组重采样时间序列是该方法的核心[5, 7-8]。对于多普勒畸变信号，由于观察者和声源的相对移动，原来固定的频率f0将会随着时间变化。此时如果以一个固定的采样间隔Δts=1/fs(fs表示采样频率)来对信号进行采样，那么在每个周期内是采样点数1/f(ti)将也会随时间变化。为了保证瞬时频率f(t)与原信号频率一致，就需要采取不固定的时间间隔，以保证在每个周期内有一个固定的采样点数n，那么时变的采样频率fs(t)和信号瞬时频率应存在如下关系：

(5)

s′=[s′(1Δts)s′(2Δts)…s′(MΔts)]=

[s(trs(1))s(trs(2))…s(trs(M))]

(6)

从多普勒信号的重采样过程中可以看出，重采样的时间间隔和重采样序列完全由瞬时频率f(t)和原始频率f0所决定，从式(2)来看，多普勒参数的估计精度，对于信号的校正工作有着重要的影响。

2多普勒信号的伪时频分析(FTFA)

上一节提到了FTFA所用到的DRDT。之所以称其为伪时频分布，是因为在一定程度上，它和传统的时频分布(Time-Frequency Distribution,TFD)有一定的相似之处。不同的是TFD显示的是信号在传统时域和频域内的能量分布，而FTFD揭示的是多普勒信号在不同时间中心和特征频率域内的能量分布情况，其能量分布峰值必然对应着原始信号的相应特征参数。为了说明分析方法，本文设置一个仿真信号的参数如下：r=2 m，S=10 m 和v=20 m/s。声源信号由700 Hz和1 000 Hz的两个幅值为1正弦信号构成：

s0(t)=sin(2π×700t)+sin(2π×1 000t)

(7)

通过式(1)可以得到如图2(a)所示的多普勒畸变信号s(t)(幅值和频率均得到调制，采样频率fs=20 kHz)，下面为其频谱，可以看出多普勒信号的频带得到明显的展宽，原始频率在频谱上已经无法分辨。图2(b)为通过短时傅里叶变换(Short-Time Fourier Transform,STFT)得到的信号时频分布，窗宽为256(本文均取此值)，白色表示能量高，黑色部分表示能量低，从分布图中可以明显的看出信号的频率随时间变化。

图2　正弦信号的多普勒畸变仿真Fig.2 Simulating signal with Doppler distortion for sinusoidal signal

信号的波形、频谱和时频分布图显示了明显的幅值和频率调制，以及频率随时间的变化趋势。但是本文需要知道精确的畸变参数(时间中心t0和特征频率f0)，以便后期的校正工作。根据式(4)的DRDT，可以得到一个新的二维矩阵DRDT(t0,f0)，即FTFA，结果完全由t0和f0的取值决定，计算结果的大小其实就暗示着信号和某一个确定的多普勒小波的相似程度，值越大表示信号与该小波相似度越高。

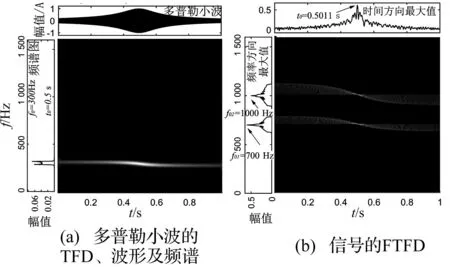
图3　多普勒小波和FTFDFig.3 Dopplerlet and FTFD

图3(a)是一个时间中心为0.5 s，特征频率为300 Hz的多普勒小波，图3(b)即为图2中对应信号的FTFD以及从时间和频率方向看去的最大幅值图。从结果中可以清晰地看到，在时间幅值图上对应的最大值出现在t0=0.501 1 s时，与仿真信号的0.5 s误差很小；频率幅值图中，两个最大值对应f01=700 Hz和f02=1 000 Hz，与仿真的预定参数吻合。其实在实际信号处理过程当中，同一声源所发出的具有不同频率的声音实际上具有相同的时间中心，因而具有接近频率的不同成分并不影响这里对时间中心的计算；但是多成分的信号必然会导致频率幅值图中具有多个峰值而且可能相邻的峰值难以辨别，但是根据式(2)和重采样时间序列的建立规则可以知道，f(t)和所选取的特征频率成正比，求比值后不会影响最终结果，所以f0的计算精度和取值对最终结果其实没有影响。这样就能够准确得到待测多普勒信号的相关参数，并将其应用于后续的畸变校正工作。

3基于FTFA的畸变校正和仿真信号分析

3.1多普勒畸变信号校正流程

根据前面的分析结果，可以总结出对一个含有多普勒畸变的轴承故障信号进行校正的具体流程(如图4)，校正步骤如下：

1) 获取具有多普勒畸变特性的原始信号和相关系统参数的测量值；

2) 对信号进行FTFA，得到信号最终的FTFD；

3) 对信号的FTFD进行极值搜索，获取待测信号的时间中心和特征频率；

4) 利用获取的参数信息结合时域重采样技术对信号的多普勒畸变进行校正，得到校正后的信号；

5) 对校正后的信号进行解包络得到包络谱，从而分析得到轴承的故障类型和相关诊断结果。

图4　多普勒畸变信号校正和诊断流程Fig.4 Scheme of the proposed method

3.2仿真信号的校正分析

在第2节中最终得到了待测信号的时间中心和特征频率，但这并非方法的最终目的，本文希望通过这些参数来去除信号的多普勒畸变，从而为后续的解包络诊断提供可能性。

式(5)中，不妨取f0=700 Hz，t0=0.501 1 s。此时信号的瞬时频率f(t)由式(2)决定，也将变为已知，又由于fs=20 kHz，可以计算得到重采样时间间隔Δti和重采样时间序列trs，再通过三次样条对原始信号进行插值，得到trs的各个时刻所对应的信号值，进而得到重采样信号s′(t)如图5所示，其中图5(a)为信号的时域波形和频谱，图5(b)为信号的时频分布。对比图2和图5，特别是从频谱图和信号的时频分布中，明显可以看到，原始信号的两个频率均得到了很好的校正，在频域中频带集中，对应的特征频率容易辨别，在得到这样的信号后，后续的相关频域和包络诊断分析为可能。

图5　校正信号的时频图Fig.5 Corrected signal in time and frequency domain

4道旁轴承故障实验信号分析

为进一步验证这里所提出方法的有效性，本文对轴承型号NJ(P)3226XI的列车滚动轴承的多普勒试验信号进行相关处理，该型号为我国列车使用的单列向心短圆柱滚子轴承主要型号，其详细参数如表1所示。

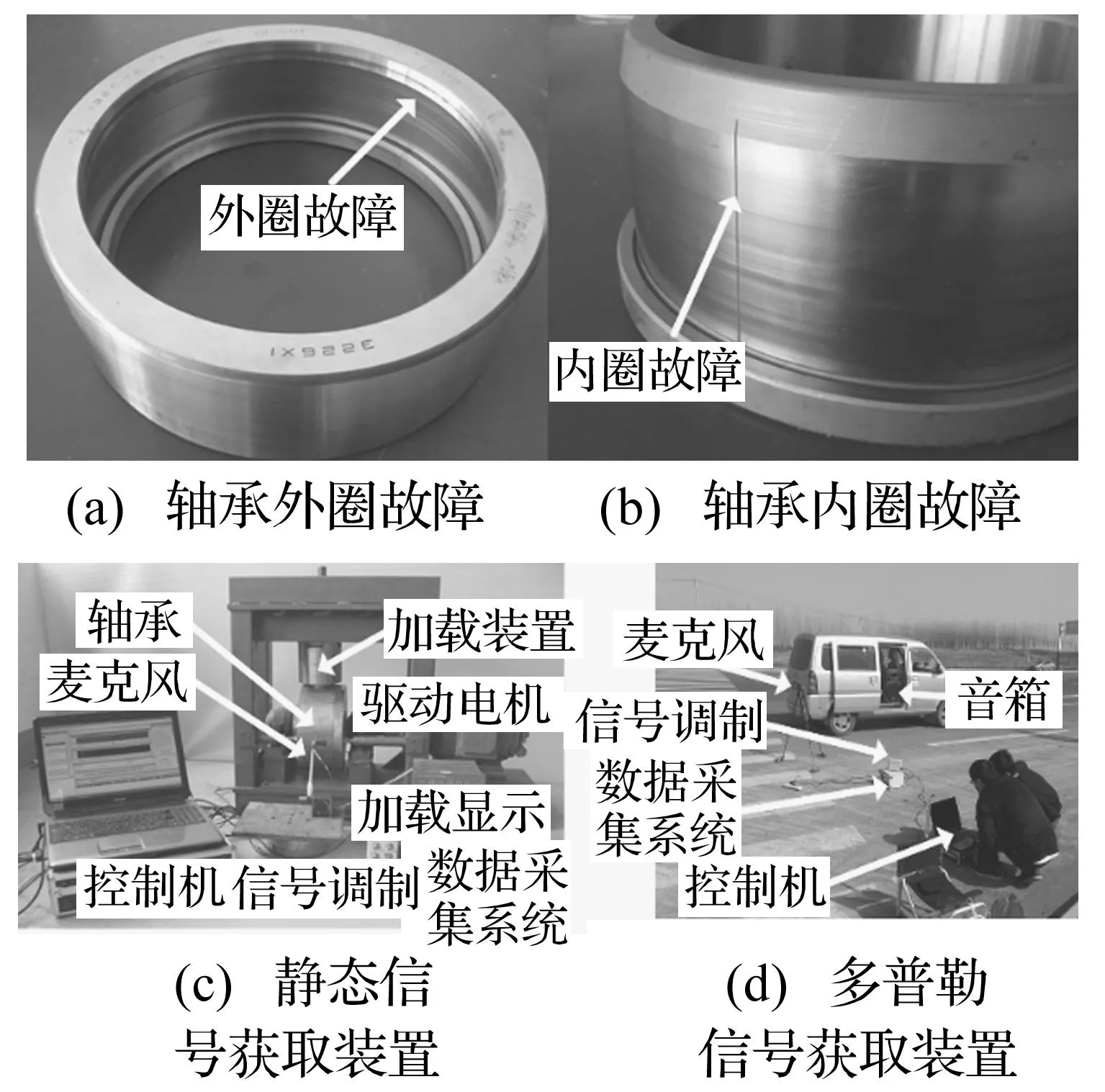
图6　实验装置Fig.6 Experimental facility

实验主要由两部分组成：① 基于该型号轴承本项目组自行设计了一套实验平台如图6(c)所示，该平台中所使用的麦克风选用丹麦BK公司的声压场麦克风4944-A，采集卡选用美国NI 公司的PXI-4472动态信号采集模块，采集箱选用美国NI公司的PXI-1033机箱。为了获取轴承故障，本文采用线切割方式人为加工形成轴承内外圈的切缝均为0.18 mm的故障如图6(a)、(b)所示。实验中电机转速设置为1 430 r/min，轴承加载负荷为3t，采样频率为50 kHz，从而就可以获取到轴承故障的静态声学信号；② 第二步将前面采集得到的信号通过安放于汽车上的音箱播放出来，同时汽车以约30 m/s(108 km/h)的速度沿直线行驶，麦克风安放于距离汽车行驶路线垂直距离约2 m处，整个实验装置如图6(d)所示，这样，麦克风采集到的信号就是受到多普勒畸变严重影响的轴承故障信号，我们需要做的就是从采集的信号中恢复出原始信号并进行故障诊断，确定故障类型等信息。

表1　NJ(P)3226X1轴承相关参数

另外通过表1中的数据，很容易计算得到轴承的内外圈故障频率的理论值分别为138.7 Hz和194.9 Hz。

4.1轴承外圈故障诊断

如图7所示为实验获取的轴承外圈故障多普勒畸变信号的时域波形和经过STFT得到的TFD，可以清楚地看到，信号的幅值受到了明显的调制，在时频分布图中，信号的多个频率成分得到显现，但是由于多普勒畸变的影响，值都随时间变化不断改变。

图7　外圈故障多普勒信号时域波形和TFDFig.7 Outer-race defect Doppler signal waveform and TFD

利用本文所提出的FTFA对原始信号进行分析，可以得到如图8(a)所示的信号FTFD，从时间轴方向看去，取所有频率对应的最大幅值(上图)，可以得到一个明显的峰值，对应的时间为t0=0.162 8 s即为信号的时间中心；再将时间固定在t0，从频率方向观察，可以得到左图所示的频率分布，其中可以看到几个较高的频率分量(具体值如表2所示)，本文取f0=1 256 Hz作为特征频率。

图8　外圈故障信号的FTFD和校正后的TFDFig.8 FTFD of original signal and the corrected output TFD

确定这两个参数之后，利用前面所提到的重采样方法对原始信号进行重采样，从而对多普勒畸变加以校正。重采样得到校正后的信号，对信号进行STFT得到其TFD如图8(b)所示，可以看出主要的频率分量已经不随时间改变，也即多普勒畸变得到了有效的校正。接下来对校正后的信号分别做频谱分析和包络分析，结果如图9(c)、(d)所示，作为对比，对原始信号直接做频谱分析和包络分析，结果如图9(a)、(b)所示。比较两组结果，很明显的可以看出，对未校正的信号(原始信号)直接分析，由于多普勒畸变的影响，频谱和包络谱上的频率都出现扩展现象，导致无法判断故障频率；而经过校正后的信号的频谱上有明显的几条高能量谱线，包络谱上可以清楚地看到故障频率fc=138.9 Hz，与理论结果138.7 Hz非常相近。

图9　原始信号和校正后信号的频谱和包络谱Fig.9 Spectrum and envelope spectrum of original signal and corrected signal

4.2轴承内圈故障诊断

接下来同样利用所提出的方法对轴承内圈故障多普勒畸变信号进行处理，如图10所示为原始信号的时域波形和TFD，与外圈相似，可以看到明显的频率和幅值调制。对原始信号直接进行频谱和解包络分析，得到的结果如图12(a)、(b)所示，频谱上的频率出现展宽，包络谱由于多普勒畸变的影响，故障频率互相混叠，无法辨别。

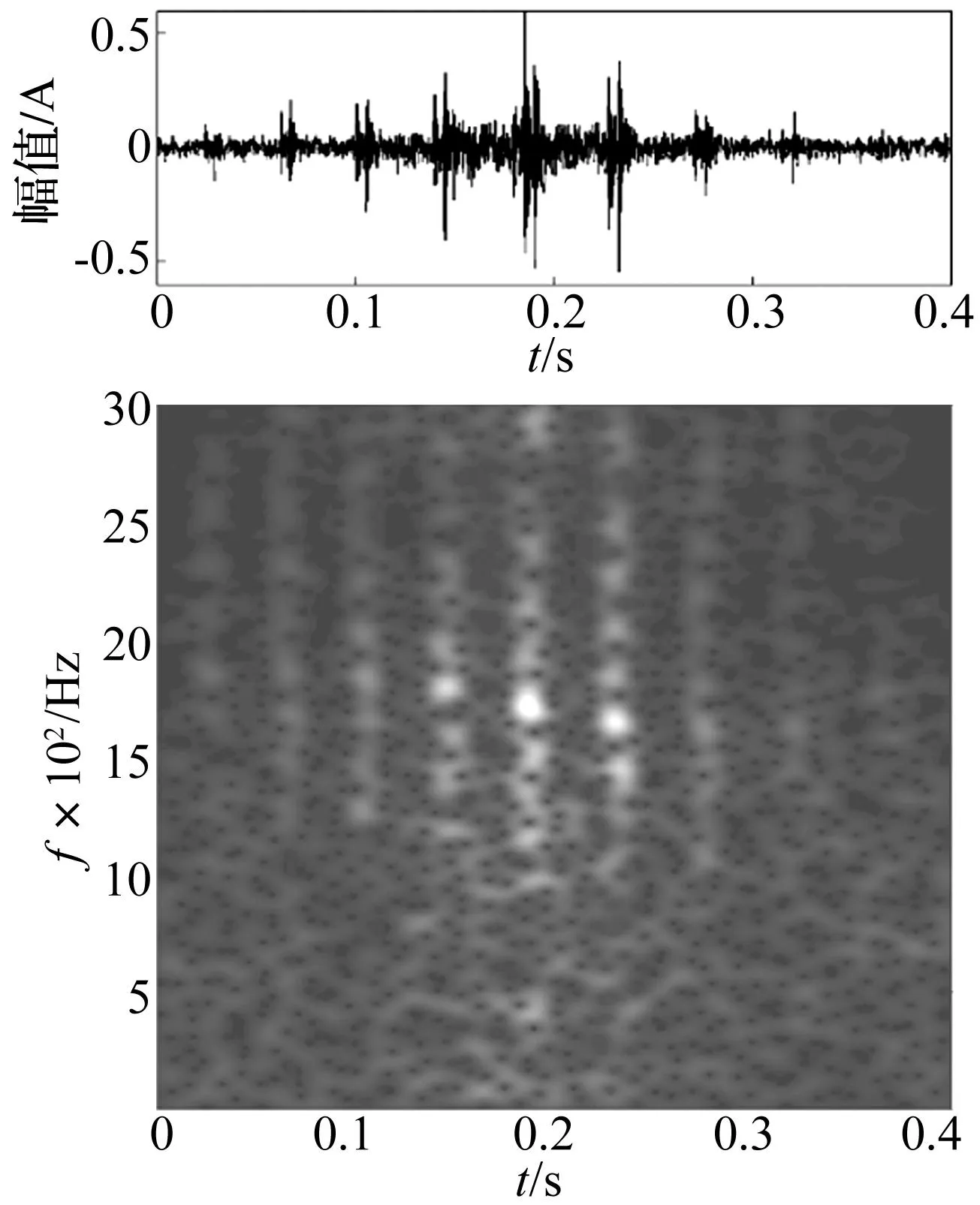
图10　内圈故障多普勒信号时域波形和TFDFig.10 Inner-race defect Doppler signal waveform and TFD

利用本文所提出的FTFA对原始信号的FTFD求解，得到如图11(a)所示的结果，从时间方向的最大值来看，得到多普勒信号的时间中心t0=0.169 1 s，将时间固定于t0，得到该时刻的频率分布如左图，由于内圈故障的复杂性，所含的特征频率成分比较多，但仍然可以辨别几条明显的谱线，其频率值如表2所示，取f0=1 736 Hz作为特征频率。利用这两个参数通过重采样对多普勒畸变进行校正，得到校正信号的TFD如图11(b)所示，可以看到校正后的时频分布明显均匀，主要频率成分的频率值也不随时间变化。

图11　内圈故障信号的FTFD和校正后的TFDFig.11 FTFD of original signal and the corrected output TFD

最后，和外圈故障信号一样，对校正后的信号进行频谱和包络谱分析，得到的结果如图12(c)、(d)所示。对比原始信号和校正后信号的分析结果，可以看出原始信号的频谱和包络谱混叠在经过多普勒校正之后都得到了很好的消除，在图12(d)的包络谱中，内圈故障信号特征频率fi=195.3 Hz已经清晰可见，这与其理论结果194.9 Hz也较好的保持一致，实验结果再次证明本文所提出的方法在对列车轴承故障多普勒信号的校正和诊断中的有效性。

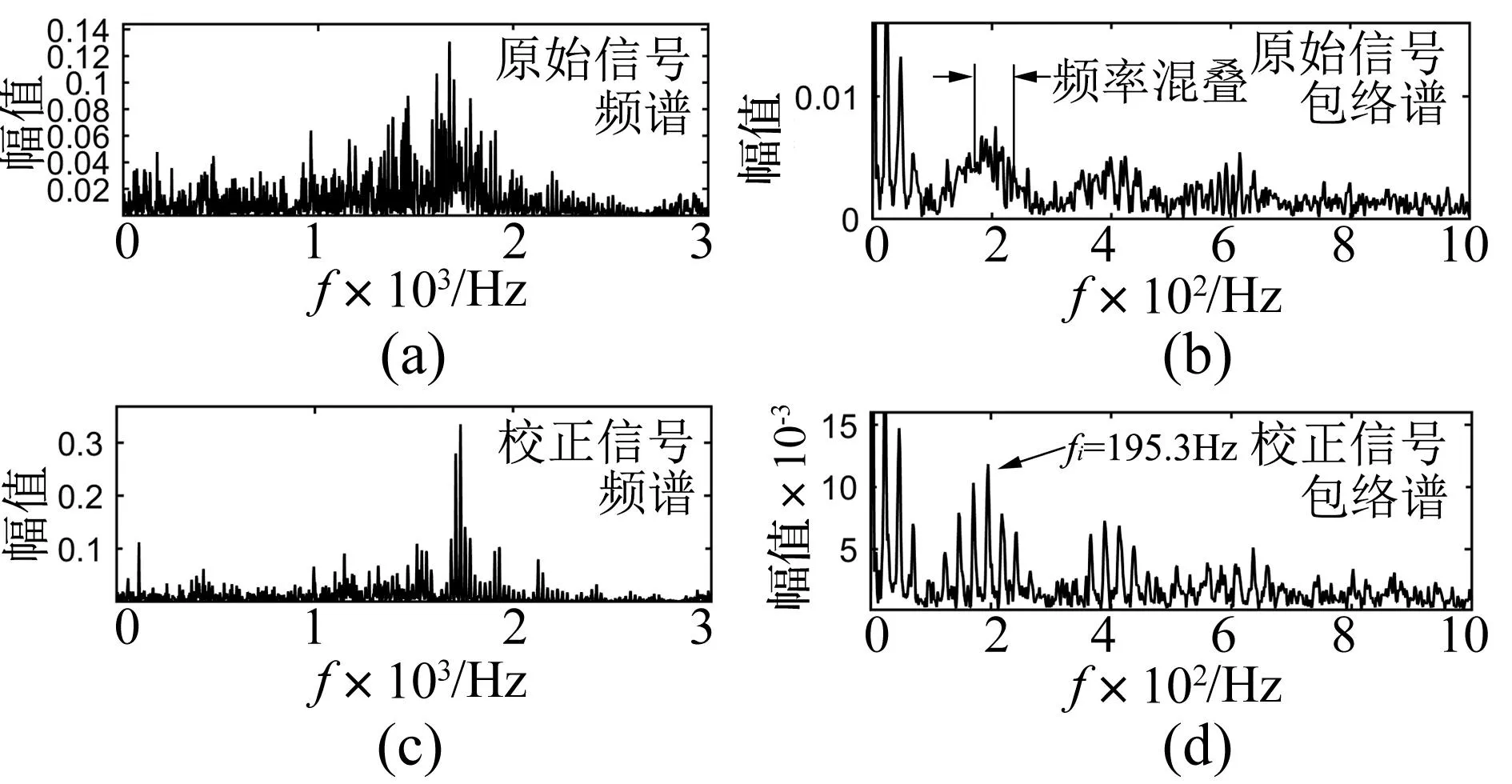
图12　原始信号和校正后信号的频谱和包络谱Fig.12 Spectrum and envelope spectrum of original signal and corrected signal

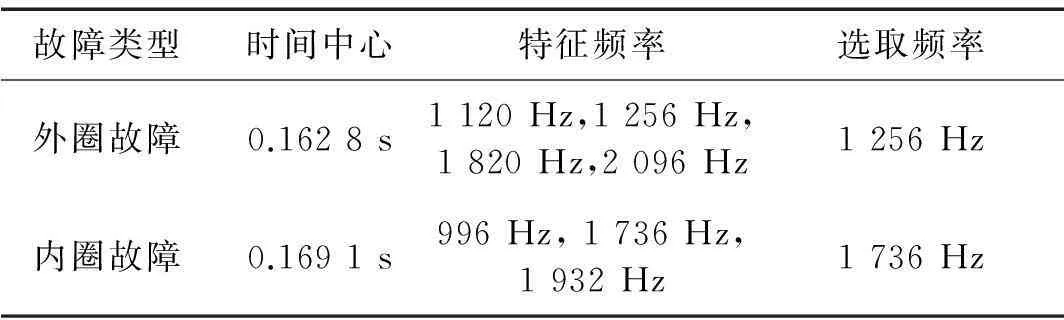
故障类型时间中心特征频率选取频率外圈故障0.1628s1120Hz,1256Hz,1820Hz,2096Hz1256Hz内圈故障0.1691s996Hz,1736Hz,1932Hz1736Hz

5结论

针对列车与道旁监测麦克风之间相对高速运动带来的多普勒效应给列车轴承声音信号的频带扩展、频移和幅值调制等问题，以及该畸变给信号分析和诊断带来的不利影响，本文提出了一种利用伪时频分析来获取多普勒信号的伪时频分布的方法，进而获得多普勒声学信号的两个重要参数，利用该参数结合重采样方法对信号的多普勒畸变加以校正，得到了可以有效获得故障特征的信号，为列车轴承道旁声音监测故障诊断提供了一种有效、可行的方法。仿真信号和实验信号的分析结果以及对存在故障的轴承多普勒畸变信号的故障频率的准确计算和判断结论表明，该方法对该类畸变信号的校正和诊断切实可行。

同时，方案是基于对信号频谱的能量积分，克服了噪声和偶然高能频率分量的影响，避免了基于TFD的峰值搜索或者能量重心法中算法发散的问题，作为一种全局结果获取的方法，不需要考虑传统参数搜索算法的收敛性，进一步增加了方法的可行性。但是该方法需要预先测量模型的相关参数(声源速度和垂直距离)，给诊断工作带来一定的不方便，笔者也将在后期的工作中继续研究如何避免对这些参数的依赖，以期对算法的进一步完善。

参 考 文 献

[ 1 ] Tandon N, Choudhury A. A review of vibration and acoustic measurement methods for the detection of defects in rolling element bearings[J]. Tribology International, 1999, 32(8):469-480.

[ 2 ] Irani F D. Development and deployment of advanced wayside condition monitoring systems[J]. Foreign Rolling Stock, 2002, 39(2):39-43.

[ 3 ] Choe H C, Wan Y, Chan A K. Neural pattern identification of railroad wheel-bearing faults from audible acoustic signals: comparison of FFT, CWT, and DWT features[J]. SPIE Proceedings on Wavelet Application, 1997, 3078:480-496.

[ 4 ] Cline J E, Bilodeau J R, Smith R L. Acoustic wayside identification of freight car roller bearing defects[C]//Proceedings of the 1998 Asme/Ieee Joint Railroad Conference,1998:79-83.

[ 6 ] 刘方, 沈长青, 何清波, 等. 基于时域多普勒校正和EEMD的列车轴承道旁声音监测故障诊断方法研究[J]. 振动与冲击, 2013, 32(24):104-109.

LIU Fang, SHEN Chang-qing, HE Qing-bo, et al.Wayside acoustic fault diagnosis for locomotive bearings based on Doppler effect correction and EEMD method in time domain [J]. Journal of Vibration and Shock, 2013, 32(24):104-109.

[ 7 ] 张翱, 胡飞, 沈长青, 等. 基于能量重心法的列车轴承多普勒畸变故障声信号校正诊断研究[J]. 振动与冲击, 2014,33(5):1-7.

ZHANG Ao, HU Fei, SHEN Chang-qing, et al. Doppler distortion removal based on energy centrobaric method for wayside fault diagnosis of train bearing by acoustic signals [J].Journal of Vibration and Shock, 2014,33(5):1-7.

[ 8 ] He Qing-bo, Wang Jun, Hu Fei, et al. Wayside acoustic diagnosis of defective train bearings based on signal resampling and information enhancement[J]. Journal of Sound and Vibration, 2013, 332(21):5635-5649.

[ 9 ] Dybala J,Radkowski S. Reduction of Doppler effect for the needs of wayside condition monitoring system of railway vehicles[J]. Mechanical Systems and Signal Processing, 2013, 38(1):125-136.

[10] 邹红星, 周小波, 李衍达. 采用Dopplerlet基函数的时频信号表示[J]. 清华大学学报:自然科学版, 2000(3):55-58.

ZOU Hong-xing, ZHOU Xiao-bo, LI Yan-da.Time-frequency signal representation with Dopplerlet basis functions [J]. J Tsinghua University Science and Technology, 2000(3):55-58.

[11] Zou H, Songa S, Liu Z, et al. Acceleration-based Dopplerlet transform-Part I: Theory[J]. Signal Processing, 2008, 88(4):934-951.

Fake time-frequency analysis of acoustic signals with Doppler distortion and its correction

ZHANGHai-bin,LUSi-liang,HEQing-bo,KONGFan-rang(University of Science and Technology of China, Hefei 230027, China)

Abstract:There exist Doppler distortion phenomena in acoustic signals of a moving acoustic source acquired with a microphone at its wayside, the signal analysis is more difficult, especially, for the wayside acoustic fault diagnosis of a high speed train. To improve the correctness and reliability of diagnosis, a fake time-frequency analysis (FTFA) for Doppler signals based on Morse acoustic theory was proposed. FTFA provided a fake time-frequency distribution (FTFD), the time center and characteristic frequencies of a signal were estimated effectively with this distribution. The estimated parameters were utilized in signal resampling to correct its Doppler distortion. The corrected signal was analyzed to extract fault information expediently. Both simulation and test results indicated that the proposed method can be used to estimate Doppler distortion signals’ parameters effectively and correct the signals, this method has a good application prospect for the wayside acoustic fault diagnosis.

Key words:fault diagnosis; Doppler distortion; acoustic signal; fake time-frequency analysis

中图分类号:TH165+.3；TB52+9

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.05.003

通信作者何清波 男，副教授，博士生导师，1980年5月生

收稿日期：2014-12-11修改稿收到日期：2015-03-11

基金项目：国家自然科学基金资助项目(51475441;11274300)

第一作者 张海滨 男，博士生，1989年10月生