基于虚拟体的弹炮刚柔耦合动力学优化设计研究

陈世业， 潘玉竹， 王兰志， 魏　巍， 原慧敏(.北京航天发射技术研究所，北京　00076; .长治清华机械厂，山西　长治　0460)



基于虚拟体的弹炮刚柔耦合动力学优化设计研究

陈世业1， 潘玉竹1， 王兰志1， 魏巍1， 原慧敏2(1.北京航天发射技术研究所，北京100076; 2.长治清华机械厂，山西长治046012)

摘要：为了研究火炮系统结构参数对弹丸膛内运动和炮口扰动的影响，通过引入虚拟体，提出了一种充分反映弹炮间相互作用的火炮动力学建模方法，推导了含虚拟体项的自行火炮刚柔耦合动力学方程；同时，以某型履带式自行火炮为例，引入多目标优化算法，建立了以弹丸和炮口初始扰动为目标函数的火炮系统多目标优化设计模型，获得了在相同射击条件下试验测试数据和仿真计算结果的对比曲线，以及结构参数的优化结果。分析表明，采用该方法建立的模型能较真实地反映火炮系统的动态响应特性和弹丸的膛内运动规律，且在考虑弹丸与柔性身管接触碰撞的前提下实现了弹丸和火炮运动的多目标优化设计，可以为自行火炮的发射动力学研究提供一定参考。

关键词：虚拟体；弹炮；刚柔耦合；多目标优化

自行火炮进行射击时，身管的弹性振动和弹丸运动两者相互耦合作用，形成了火炮的初始扰动并决定了弹丸出炮口时刻的初始状态，因此建立相对准确高效的火炮系统刚柔耦合动力学模型[1]，来分析火炮结构参数对弹丸运动状态和炮口初始扰动的影响，并提出相应的优化设计方案用于降低弹丸出炮口时刻的系统振动，对火炮的发射动力学[2]研究具有重要的指导意义。

从目前的研究状况来看，在火炮动力学仿真建模过程中[3-4]，一般忽略弹丸和柔性身管的耦合影响，将弹丸对身管的作用力等效为外界激励施加于火炮模型，并取火炮的炮口初始扰动作为系统优化目标[5-6]，即求解在满足一定战术指标下具有较小炮口起始扰动的火炮结构最佳设计方案。

炮口初始扰动的降低将有利于提高火炮系统的射击稳定性，但火炮的射击精度最终是由弹丸的运动状态来决定，同时，由于弹丸和弹性身管的接触区域在随时变化，即柔性体[7]的边界条件在不断改变，如何在火炮动力学模型中充分考虑弹丸和火炮的耦合作用，从而得出火炮结构参数对弹丸运动的影响，将助于指导火炮的结构设计。

针对上述问题，本文通过引入虚拟体的概念，提出了一种基于虚拟体的弹炮刚柔耦合[8-9]模型建模方法，并将其引入到自行火炮动力学模型中，结合算例和试验结果进行对比，验证了该方法的有效性；同时，将多目标优化算法与动力学模型相结合，提出了综合反映弹丸运动姿态和炮口振动的火炮系统多目标优化模型，并给出了设计变量范围内的优化设计方案。

1基于虚拟体的弹炮刚柔耦合模型

首先引出文中虚拟体的概念，即假想的无质量无转动惯量的刚性体，在动力学仿真模型中可以通过将刚体的质量和转动惯量设为极小值来代替。本文提出的基于虚拟体构建的弹炮刚柔耦合系统拓扑关系如图1所示。

具体描述如下：由有限个虚拟体组成模拟身管，其中模拟身管的几何模型对应于真实身管的实体外形，虚拟体两端以球铰(h9-h12)形式联接在经过模态解析的柔性身管单元上，相邻虚拟体间以扭转弹簧力(h5-h8)限制其绕身管轴线方向的相对转动；柔性身管两端分别与炮尾和炮口制退器固连(h13-h14)。

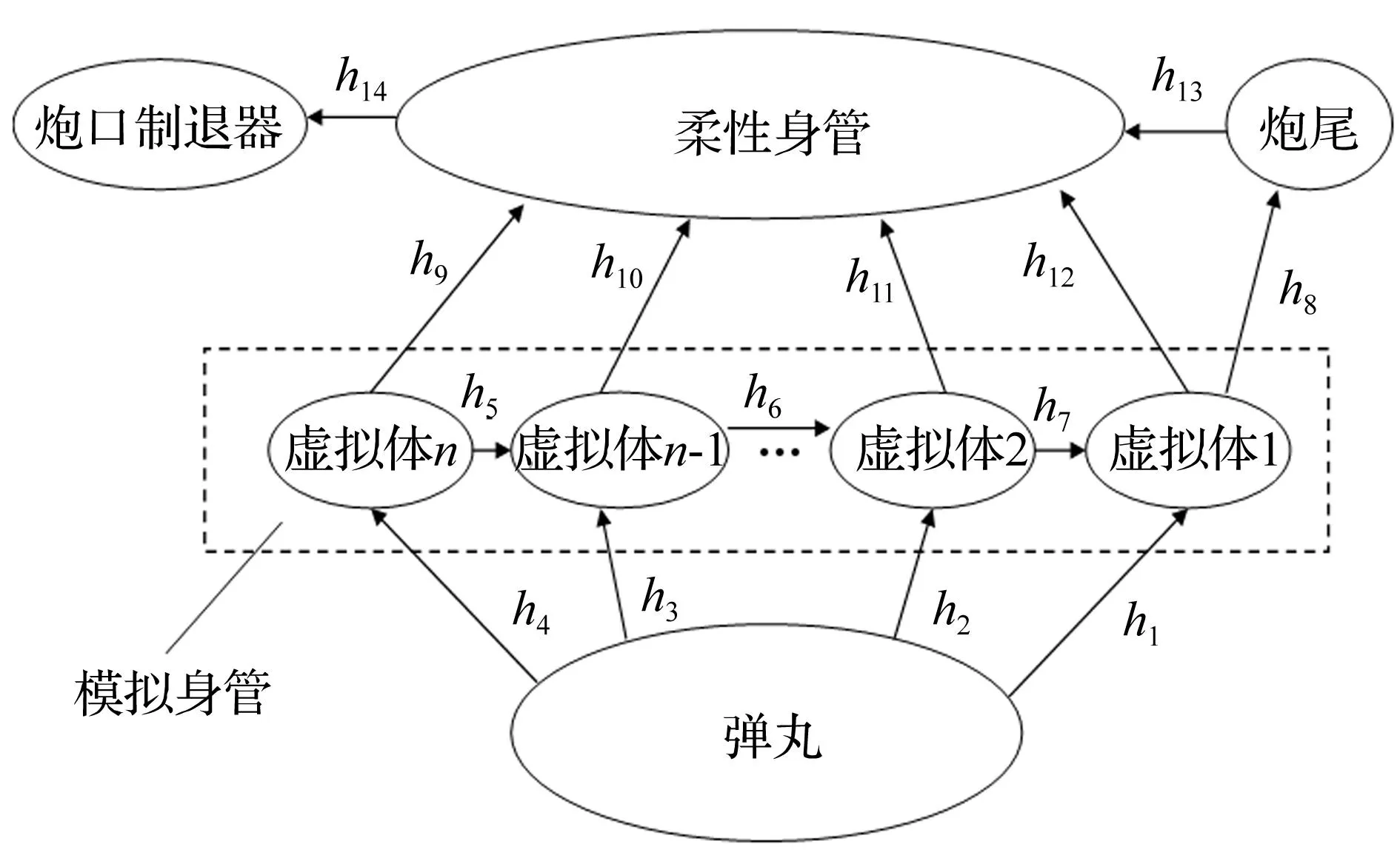
图1　基于虚拟体的弹炮刚柔耦合系统拓扑图Fig.1 Topological relation of the projectile-barrel system

弹丸在模拟身管中运动时，弹带和弹丸前定心部与虚拟体内壁发生接触碰撞，相互间的作用力(h1-h4)将通过虚拟体传递到柔性身管单元上，并反馈给弹丸运动。

最终建立的弹炮刚柔耦合模型见图2所示,其中，柔性身管在模型中采用模态法描述身管的弹性变形，即将事先经过有限元模态解析的柔性身管单元(梁单元)代入系统模型，通过模态振型的叠加来获得对应的应力和应变。

图2　基于虚拟体的弹炮刚柔耦合模型Fig.2 The projectile-barrel system model including virtual substances

对于图2所示的弹炮刚柔耦合系统，共由n+4个构件组成，包括了柔性身管、弹丸、炮尾、炮口制退器和n个虚拟体。

系统中任意第i个柔性体或刚体，其对应的动力学控制方程为

(1)

式中:Ti为动能，cqi为构件对应的运动约束矩阵Cqj对广义坐标的偏导数，λ为拉格朗日乘子，Fi为广义力。

取广义坐标矢量：

(2)

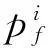
将动能表达式代入式(1)，并化简得：

(i=1,2,…,n+4)

(3)

式中:Mi为质量矩阵，Fsi、Fvi和Fei分别为应变能、力引起的速度和外加载荷所引起的广义力，其中虚拟体并不产生应变能。

将系统中所有构件产生的运动方程组与构件间的约束方程联立，即构成了基于虚拟体的弹炮刚柔耦合多体系统的动力学方程，写成矩阵的形式为

(4)

式中:M1为系统质量矩阵，系统约束矩阵Cq1由三部分组成，包括了柔性体与虚拟体间的柔性约束、相邻虚拟体间的刚性铰以及其他构件间的铰约束。

综上可知，系统约束矩阵Cq1和质量矩阵M1中均含有虚拟体项，则当弹丸在模拟身管中与虚拟体发生接触碰撞，两者的相互作用力将以广义力的形式传递到系统的动力学方程中，从而影响身管的弹性振动，并反馈给弹丸运动。

2自行火炮多体动力学模型

根据自行火炮实际射击的物理过程，将其划分为火力部分和底盘部分，火力系统包括后坐部分(身管、制退器和炮尾)、摇架、高低机、方向机和炮塔等；底盘行动部分包含车体、推进装置、悬挂装置等，其中推进装置由主动轮、履带、诱导轮及履带调整器、负重轮和托带轮组成。

将基于虚拟体构建的弹炮刚柔耦合系统引入自行火炮系统中，则构件间的拓扑关系如图3所示。

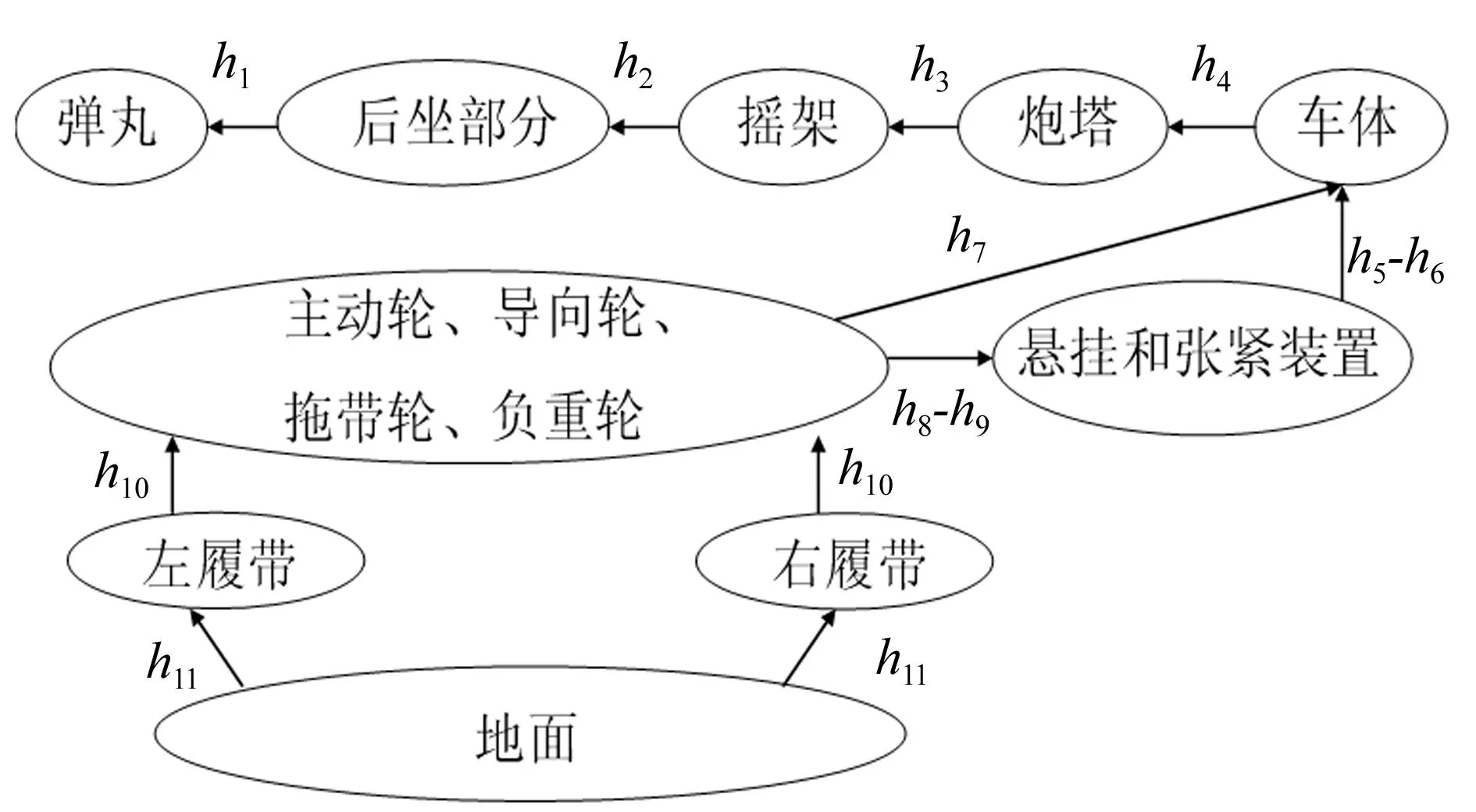
图3　自行火炮系统拓扑图Fig.3 Topological relation of the self-propelled artillery

图3中，h表示部件间的相对关系。h1为后坐部分与弹丸间的连接，主要表现为由虚拟体组成的模拟身管和弹丸之间的约束，在图1中已有详细介绍；h2为后坐部分与摇架间的接触碰撞力和反后坐力；h3为摇架与炮塔间的旋转铰、平衡机力与高低机力；h4为炮塔与车体间的万向节和方向机力；h5为悬挂系统和车体间旋转铰、扭转弹簧力和阻尼力；h6为张紧装置和车体间固定约束；h7为主动轮、拖带轮和车体间旋转铰；h8为负重轮与悬挂装置间的旋转铰；h9为导向轮与张紧装置间的旋转铰；h10为履带板间的场力以及履带系统与各轮间的约束和力元；h11为地面与履带间的作用力。

设自行火炮系统共有m个构件组成，其中包括了n个虚拟体，1个柔性身管，(m-n-1)个刚性构件，则自行火炮系统的动力学控制方程可由式(3)进行扩展求得，即：

(i=1,2,…,m)

(5)

(6)

式中:Ui为构件具有的势能。

将自行火炮系统所有m个构件的运动和约束方程联立，写成矩阵的形式为：

(7)

系统的质量矩阵M具有如下形式：

M=diag(Mv,Mf,Mr)

(8)

式中：Mv为n个虚拟构件的质量矩阵；Mr为刚性构件的质量矩阵，Mf为柔性身管在系统模型中的质量矩阵，对应的表达式形式如下：

(9)

式中：下标tt、rr和mm分别表示平动、旋转和模态自由度，nf为模态坐标的个数。

当弹丸与虚拟体发生接触碰撞时，两者的相互作用力将以广义力Fe的形式传递到系统动力学方程中。模型中由于需要考虑到柔性体的形变，在此采用基于惩罚函数的接触计算方法来计算接触力，即将接触和碰撞现象按连续的动力学问题来处理，当判断弹丸前定心部和弹带与虚拟体内壁发生接触碰撞，则法向接触力Fn计算公式为

(10)

式中：k为接触刚度系数，c为阻尼系数，δ为物体间的相对穿深量，m1、m2和m3分别为刚度指数、阻尼指数和凹痕指数。

以某型履带式自行火炮为例，引入虚拟体组成的模拟身管，建立的全炮刚柔耦合动力学模型如图4所示。整个系统共有1 116个自由度，模型中由11个虚拟体组成模拟身管，附加了22个柔性铰和11个刚性铰约束，含模态信息的柔性身管单元在炮闩前端面中心处与炮尾固连，其中，柔性身管单元取前12阶模态参与动力学计算，身管振动阻尼设为刚度系数的0.003倍，

图4　自行火炮动力学模型Fig.4 The dynamics model of self-propelled artiller

3自行火炮多目标优化模型

从目前的火炮发射动力学研究现状来看，在对整个自行火炮系统进行分析时，一般不计及弹丸和柔性身管间的耦合作用，无法获取弹丸的运动状态，因此在以提高射击精度为目标的火炮结构优化设计中，只能以降低炮口振动作为判断标准。

本文基于虚拟体建立了弹炮刚柔耦合动力学模型，综合考虑自行火炮和弹丸的运动状态，在此同时选取炮口振动和弹丸扰动作为系统的优化目标。取弹丸出炮口时刻，炮口垂向线速度vy和横向线速度vz作为炮口振动特征量，弹丸垂向角速度ωy和横向角速度ωz值作为弹丸起始扰动特征量，则自行火炮动力学优化模型所对应的目标函数可归结为

(11)

式中：vy0和vz0为未优化前的炮口振动速度初始值，ωy0和ωz0为未优化前的弹丸扰动初始值，α1、β1、α2、和β2为权重系数。

上式将弹丸和炮口的4个目标函数通过权重法进行归一化，最终得到两个优化子目标，分别为反映炮口振动量的子目标函数fp和反映弹丸初始扰动的子目标函数fd。

选取和弹炮系统直接相关的结构参数，后坐部分垂向偏心距ey、横向偏心距ez、炮口制退器质量mz、弹炮间隙b、驻退机横向布局lz和高低机等效刚度kgd作为系统设计变量。

综上，自行火炮弹炮刚柔耦合系统的多目标优化设计模型描述如下：

(12)

优化模型的建立通过Isight软件和动力学仿真模型的集成来实现，选取NSGAⅡ多目标遗传算法进行优化分析，构建的自行火炮多目标优化模型如图5所示。

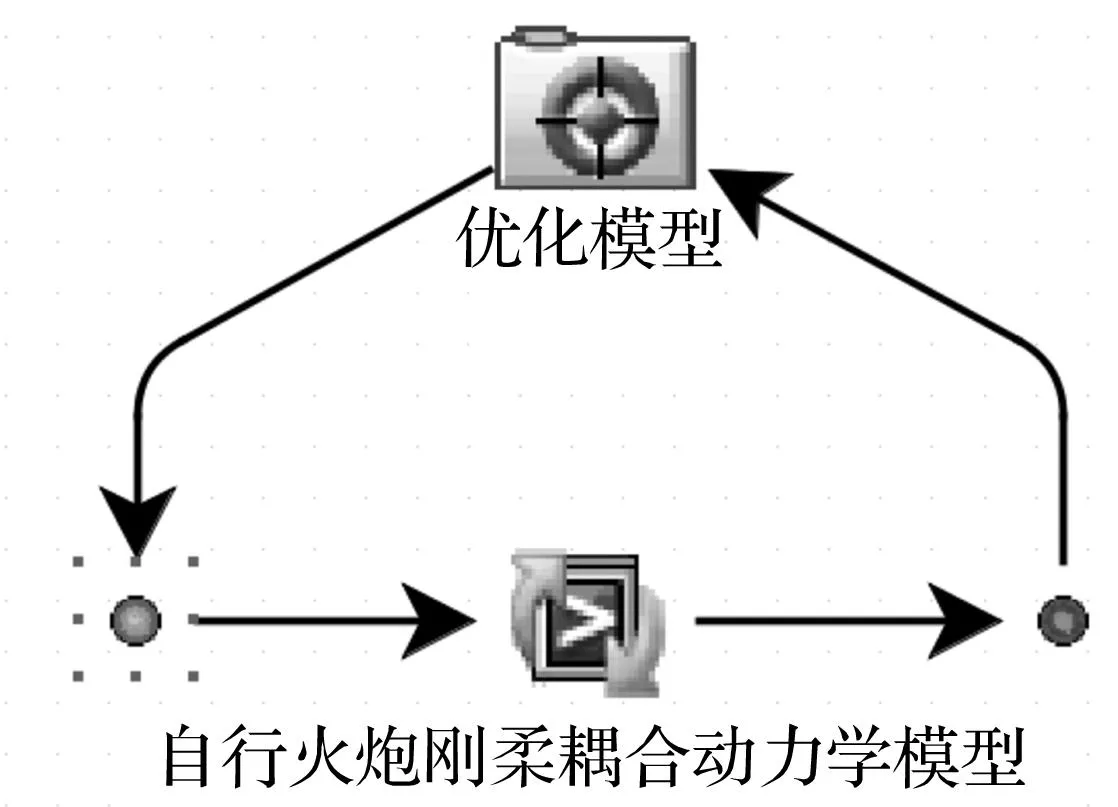
图5　自行火炮多目标优化模型Fig.5 The multi-objective optimization model of artille

在动力学模型中进行设计变量的参数化离散，并集成在Isight设计平台下，与优化模型形成闭环数据传递，共同实现仿真模型的优化求解。

4算例分析

以某型履带式自行火炮为例，某次射击试验初始条件如下：高低射角0 mil，方向射角0 mil，采用全装药底凹榴弹在常温下射击，将上述边界条件代入图4所示的自行火炮动力学模型，设变速箱输出轴与车体纵向中心平面交点处为坐标原点，水平指向车尾为x正方向，y轴方向竖直向上，z轴由右手定则确定。

仿真模型在经过静平衡计算后，在t=0.1 s时开始模拟射击，图6～图9给出了在相同射击条件下试验测试数据和仿真计算结果的对比情况，其中，图6和图7为火炮后坐位移和后坐速度的对比曲线，可以看出模型的后坐运动特性与实际情况基本相符，炮尾在t=0.7 s时复进到位。

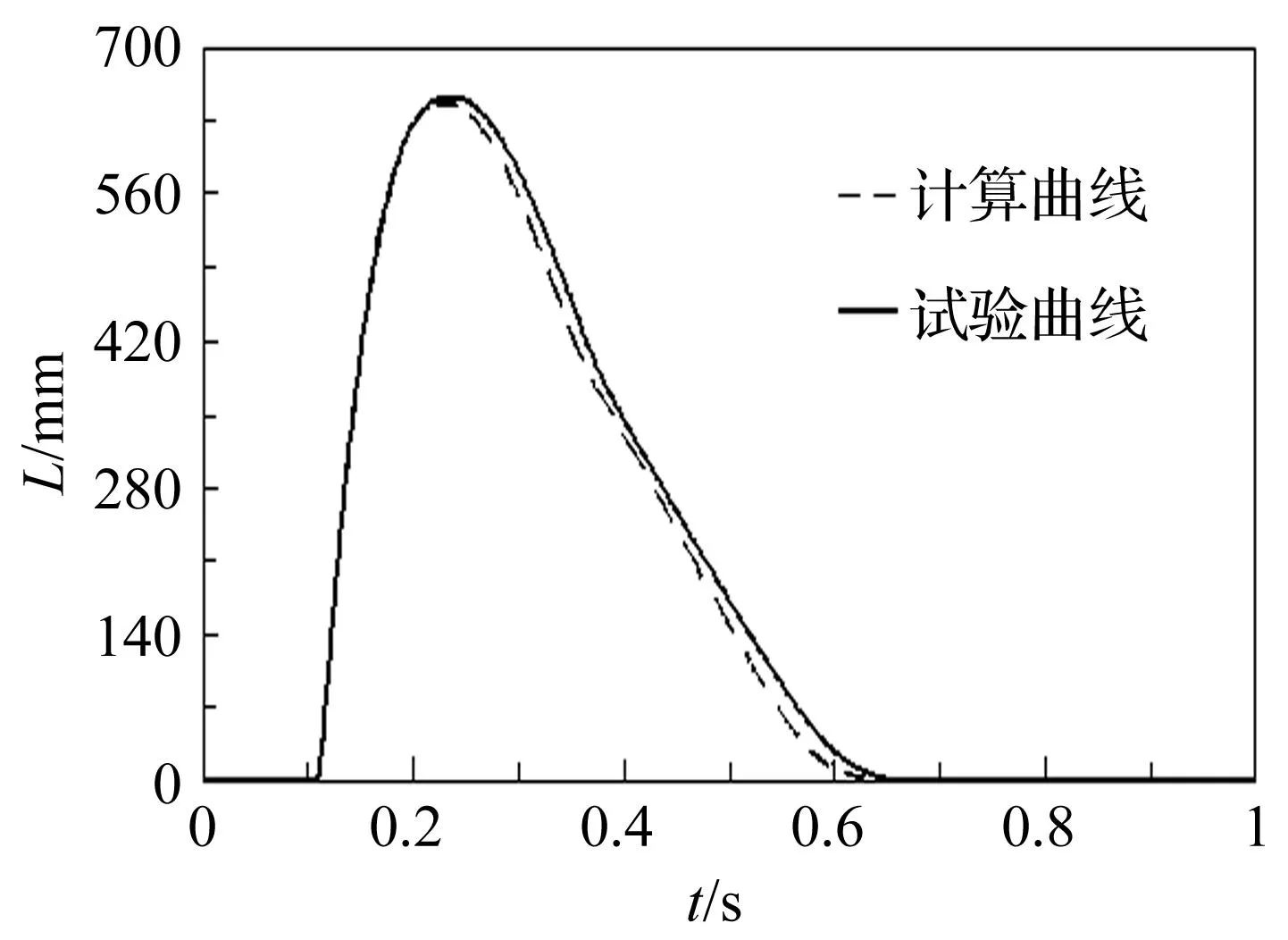
图6　后坐位移对比曲线Fig.6 The curves of recoil displacements

图7　后坐速度对比曲线Fig.7 The curves of recoil velocities

图8和图9分别为炮口垂向角位移和横向角位移的对比结果，从图中可以看出，计算得到的炮口振动规律和测试值有很好的一致性。

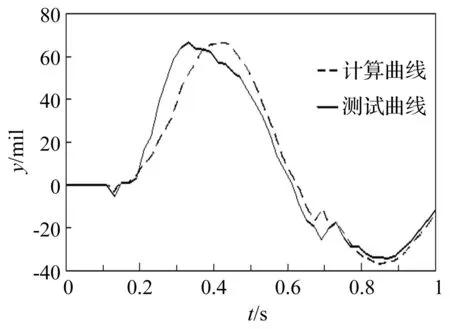
图8　炮口垂向角位移对比曲线Fig.8 The curves of vertical angular displacement

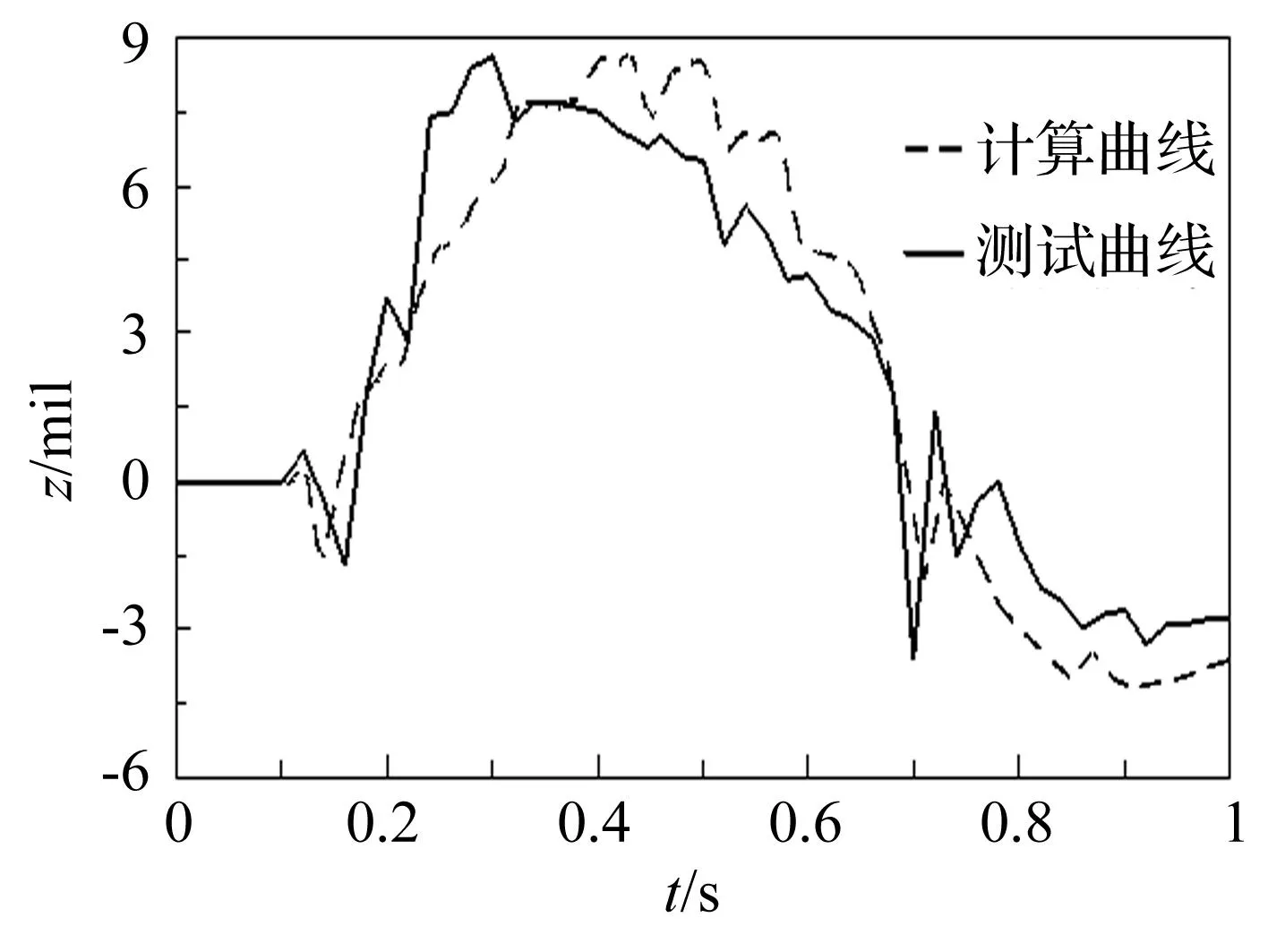
图9　炮口横向角位移对比曲线Fig.9 The curves of transverse angular displacement

图10和图11则给出了弹丸在膛内运动过程中速度的计算曲线，可知，弹丸从开始击发到离开模拟身管大约经过了12 ms(从t=0.1 s到t=0.112 s)，此时对应的弹丸初速为708.3 m/s，弹丸转速为1 435 rad/s，实测弹丸初速713 m/s，弹丸转速为1 468 rad/s，两者误差较小。

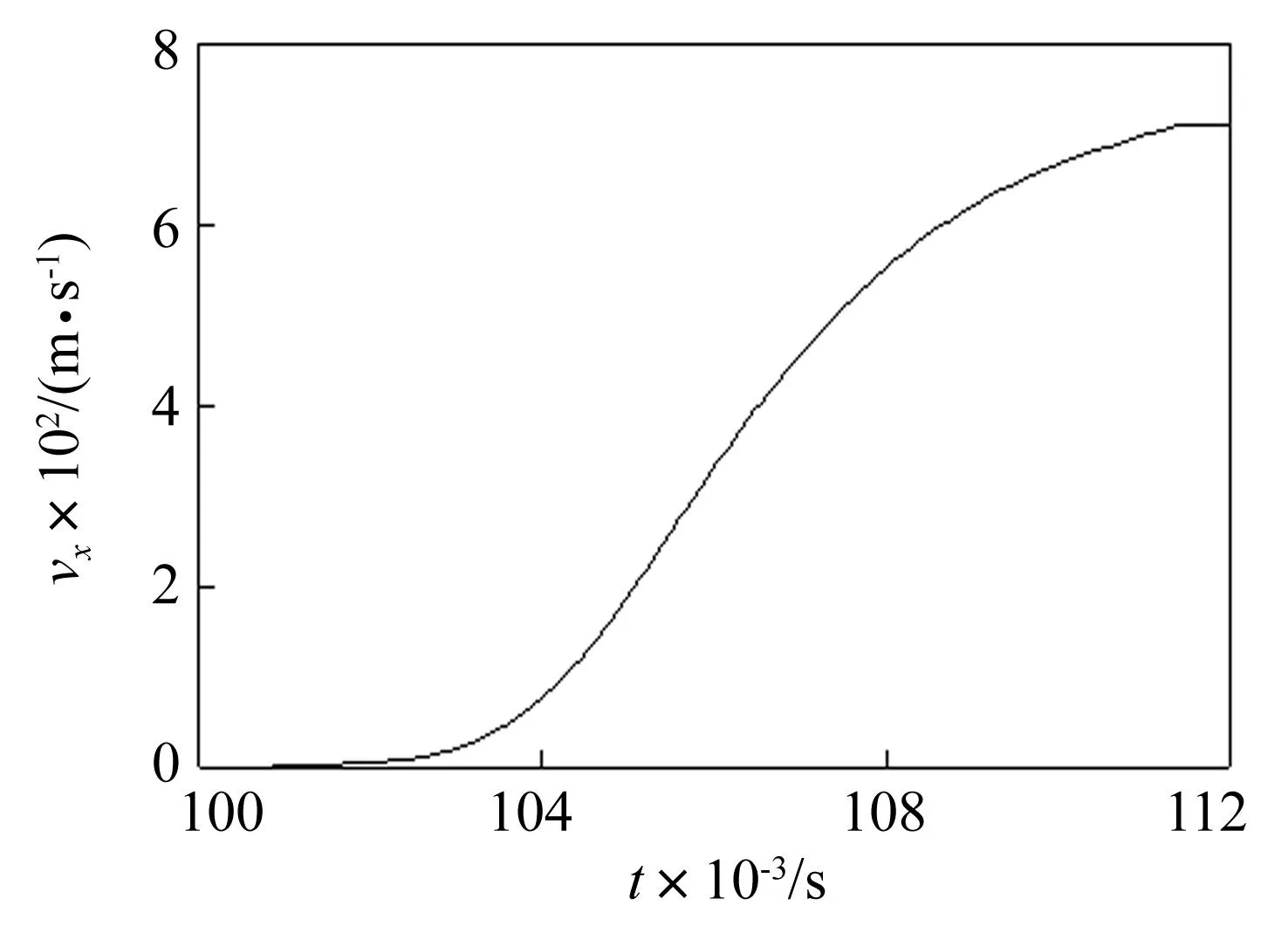
图10　弹丸vx计算曲线Fig.10 The calculated curves of ballet speed

图11　弹丸ωx计算曲线Fig.11 The calculated curves of angular speed

综上所述，仿真计算的火炮振动曲线以及弹丸运动规律和试验数据两者吻合较好，即认为将虚拟体应用到自行火炮弹炮多体系统模型中，能够较真实地反映火炮的动态响应特性，且弹丸在模拟身管中的运动变化规律与实际情况比较相符。

同时，在图5所示的优化模型中，设置NSGAⅡ算法参数如下：种群数量为30，进化50代，交叉概率0.8，变异概率0.01，即仿真模型进行变量迭代1 500次。

图12给出了炮口振动子目标函数fp和弹丸初始扰动子目标函数fd的Pareto前沿，前沿端面共包含了30个最优解，即对应30组设计变量。当目标函数趋近于A点时炮口振动较小，而在D点附近则可以获得较小的弹丸起始扰动值。

在此选取C点作为与未优化前的系统模型进行对比分析，该点对应的设计变量优化结果如下。

表1　优化结果列表

图13和图14给出了在整个弹丸膛内运动时期，炮口垂向和横向线速度的优化前后对比曲线。

火炮的射击过程中，由于各种随机因素的存在，导致炮口的振动相对较剧烈，从图中的优化结果来看，通过对自行火炮系统结构参数的合理设计，将能有效控制炮口振动。则在弹丸出炮口时刻，通过优化设计，炮口的垂向线速度vy从124.5 mm/s降至120.7 mm/s，横向线速度vz从141.9 mm/s降至64.4 mm/s。

图13　炮口垂向线速度优化对比曲线Fig.13 The optimization results of vertical velocities

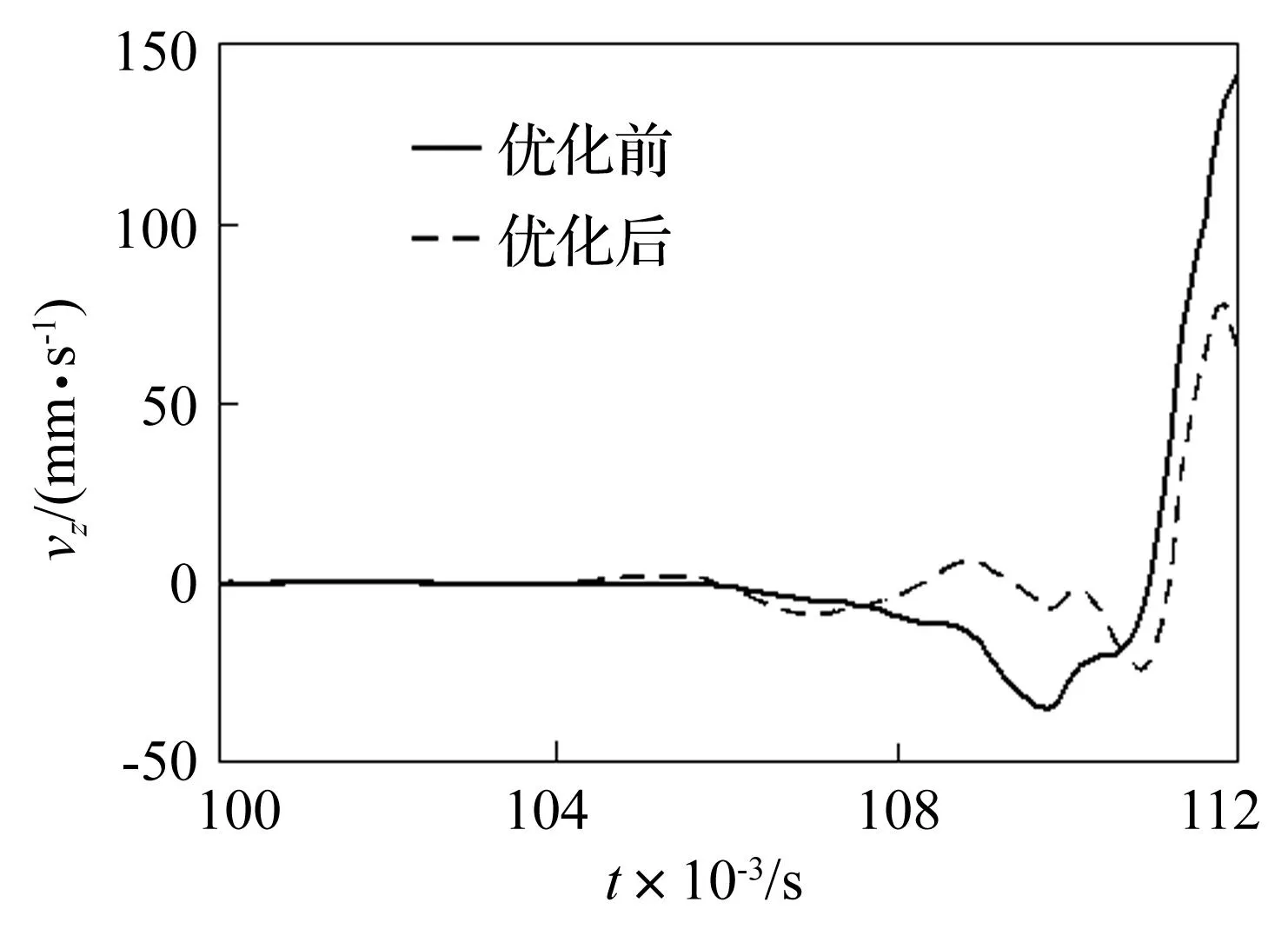
图14　炮口横向线速度优化对比曲线Fig.14 The optimization results of transverse velocities

图15和图16分别给出了弹丸的垂向和横向角速度的优化前后对比曲线。

图15　弹丸垂向角速度优化对比曲线Fig.15 The optimization results of vertical angular speed

图16　弹丸横向角速度优化对比曲线Fig.16 The optimization results of transverse angular speed

相比于初始值，在弹丸出炮口时刻，优化后的弹丸垂向角速度幅ωy从1.21 rad/s降至1.03 rad/s，横向角速度ωz从3.54 rad/s降至2.59 rad/s。弹丸出炮口时刻摆动角速度的降低，将有助于提高火炮的射击精度。

5结论

本文通过将虚拟体引入到自行火炮系统动力学模型中，建立了以弹丸和炮口运动状态为目标函数的自行火炮弹炮系统多目标优化模型，通过仿真计算和试验数据的对比分析，得到如下结论：

(1) 基于虚拟体构建自行火炮的刚柔耦合动力学模型在理论上是可行的，该模型能较真实地反映弹丸在膛内的运动规律，并可以较精确地描述火炮系统在射击过程中的动态响应特性；

(2) 采用该方法建立的模型能实现以弹丸运动状态和炮口振动为目标函数的系统优化，可以为自行火炮发射动力学研究提供一定参考。

参 考 文 献

[1] 徐达,胡俊彪,穆歌. 基于刚柔耦合的坦克炮发射动力学仿真分析[J]. 装甲兵工程学院学报,2009, 23(4): 45-47.

XU Da, HU Jun-biao, MU Ge. Simulation analysis on tank gun firing dynamics based on rigid-flexible coupling [J]. Journal of Academy of Armored Force Engineering, 2009, 23(4):45-47.

[2] 苏忠亭，徐达，李晓伟,等.小口径火炮弹炮耦合动态响应有限元时程分析[J]. 振动与冲击，2012 31(23):104-108.

SU Zhong-ting, XU Da, LI Xiao-wei, et al. Finite-element time-history analysis for dynamic response of small-caliber guns with projectile-barrel coupling[J]. Journal of Vibration and Shock, 2012, 31(23): 104-108.

[3] Huang C H, Galuski J, Bloebaum C L. Multi-objective pareto concurrent subspace optimization for multidisciplinary design [J]. American Institute of Aeronautics and Astronautics, 2007, 45(8): 1894-1906.

[4] 史跃东，王德石. 舰炮振动的刚柔耦合动力学分析[J]. 弹道学报，2010, 22(1):37-39.

SHI Yue-dong, WANG De-shi. Vibration analysis of naval gun by rigid-flexible coupling dynamics[J]. Journal of Ballistics, 2010, 22(1): 37-39.

[5] 刘伟,王晓亮,何洪文. 基于代理模型的6×6轮式平台悬架参数优化[J]. 计算机仿真, 2014, 31(6): 191-196.

LIU Wei, WANG Xiao-liang, HE Hong-wen. Optimization desgin of 6×6 wheeled platform suspension paraments based on surrogate model[J]. Computer Simulation, 2014,31(6):191-196.

[6] 葛建立,杨国来,曾晋春. 某自行火炮总体结构参数灵敏度分析与优化[J]. 火炮发射与控制学报, 2007(1): 16-19.

GE Jian-li, YANG Guo-lai, ZENG Jin-chun.Sensitivity analysis and optimization of integrated structural parameters for a type of wheeled self-propelled gun [J]. Journal of Gun Launch & control,2007(1): 16-19.

[7] Imed K, Lotfi R. Dynamic analysis of a flexible slider-crank mechanism with clearance [J]. European Journal of Mechanics A/Solids, 2008, 27(5): 885-887.

[8] 冯勇,徐振钦.某型火箭炮多形态耦合发射动力学建模与仿真分析[J].振动与冲击，2014，33(11):95-99.

FENG Yong,XU Zhen-qin. Launch dynamic modeling and simulation analysis of multi-rocket launch system with rigid-flexible coupled and rigid body-liquid coupled methods[J]. Journal of Vibration and Shock, 2014, 33(11):95-99.

[9] 张志新,胡振东.考虑弹丸与身管轴向运动耦合的火炮系统时变动力学分析[J].振动与冲击，2013,32(20):67-71.

ZHANG Zhi-xin,HU Zhen-dong.Artillery time-varing dynamic system considering coupling between bullet’s moving and barrel’s axial movement[J].Journal of Vibration and Shock,2013,32(20):67-71.

Dynamic optimization design of a projectile-barrel rigid-flexible coupled system based on virtual substance technology

CHENShi-ye1,PANYu-zhu1,WANGLan-zhi1,WEIWei1,YUANHui-min2(1. Beijing Institute of Space Launch Technology, Beijing 100076, China;2. Qinghua Machine Works of Changzhi, Changzhi 046012, China)

Abstract:In order to investigate the influences of gun structural parameters on bullet motion and muzzle disturbance, a model considering bullet-barrel interaction was set up by introducing virtual substances. The rigid-flexible coupled dynamic equation of a self-propelled gun system containing virtual substances was derived. Taking a tracker self-propelled artillery as an example, the system malti-objective optimization design model was built regarding initial disturbances of muzzle and projectile as objective functions. The comparative curves between the test data and the simulation results under the same firing condition were obtained, the optimization results of structural parameters were also gained. The results showed that this proposed model can reflect truly both the system dynamic response features and the bullet motion laws. Besides, the multi-objective design model was optimized considering bullet-barrel contact. The study results provided a reference for the launching dynamic investigation of self-propelled guns.

Key words:virtual substance; projectile-barrel; rigid-flexible coupling; multi-objective optimization

中图分类号:TJ301

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.05.024

通信作者魏巍 男，高级工程师，1981年5月生

收稿日期：2014-11-04修改稿收到日期：2015-02-16

第一作者 陈世业 男，工程师，1986年生