5-UPS/PRPU冗余驱动并联机构的内力分析与协调

周　鑫　许允斗　姚建涛　郑魁敬　赵永生

1.燕山大学河北省并联机器人与机电系统实验室,秦皇岛,0660042.燕山大学先进锻压成形技术与科学教育部重点实验室,秦皇岛,066004



5-UPS/PRPU冗余驱动并联机构的内力分析与协调

周鑫1,2许允斗1,2姚建涛1,2郑魁敬1,2赵永生1,2

1.燕山大学河北省并联机器人与机电系统实验室,秦皇岛,0660042.燕山大学先进锻压成形技术与科学教育部重点实验室,秦皇岛,066004

摘要：基于全雅可比矩阵和伪逆法求解了5-UPS/PRPU冗余驱动并联机构的内力，并提出了一种基于冗余驱动变刚度的协调内力的方法。通过求解机构的变形协调方程，得到机构的全雅可比矩阵的加权广义逆，从而求得该5-UPS/PRPU冗余驱动并联机构的内力表达式，通过有限元软件验证了该方法的正确性。以相应的5-UPS/PRPU冗余驱动并联机床为例，分析了冗余分支驱动刚度的变化对各个分支内力幅值的影响，进而提出了一种协调内力的方法。通过分析其内力随冗余分支刚度的变化分布情况可知，非冗余分支各个驱动螺旋以及冗余分支约束螺旋所对应的内力幅值可以通过在一定程度上增大冗余分支的驱动刚度来降低。该方法对机械结构设计人员以及控制系统搭建人员在提高系统精度、降低系统内力方面有重要的参考价值。

关键词:并联机构;冗余驱动;变刚度;内力

0引言

冗余驱动指机构的驱动数目大于其本身的自由度数目[1-2]。冗余驱动机构由于可以消除并联机构的奇异位形[3]，提高系统动态响应特性[4]，并且通过协调分配各个分支的驱动力，从而达到降低各个分支负载的效果[5]，因此被广泛应用于地震模拟器或机床[4-6]等对承载能力以及运动精度具有较高要求的场合。然而，由于驱动数目大于末端执行器的自由度数，往往存在因驱动力分配不当而产生内力较大的现象，造成机构的损坏，冗余驱动并联机构的应用也因此受到了制约。因此，有必要对冗余驱动并联机构的内力进行深入分析，并通过冗余分支协调其他非冗余分支的驱动力，从而有效降低或消除内力。

现有的文献对于冗余驱动并联机构的内力已经有了初步的认识和理解，文献[6]通过引入多机械手抓取物体时所产生的内力的概念，将并联机构的内力定义为动平台内部受到的弯扭、拉压等状态。尽管该定义广泛应用在多机械手的协同工作中，但难以体现并联机构中各个驱动分支的输入力间的相互制约。文献[7]给出了冗余驱动并联机构的内力定义，并且针对并联机构的三种不同情况(非冗余机构非奇异位置、非冗余机构奇异位置和冗余机构)分别进行了说明。文献[8]提出了一种求解冗余驱动并联机构内力的方法，并且以锻造操作机机构2SPS+R为算例，讨论了机构内力与变形协调间的关系。文献[9]针对液压驱动冗余振动台内力耦合的问题，通过协调控制各个激振器间的作用力，从而达到减小各个激振器间的内力耦合的目的。文献[10]提出了一种通过冗余内力提高并联机构实际精度的方法，并且通过实验进行了验证。可见，目前对冗余驱动并联机构内力的研究并不多，且对于如何有效降低内力对机械系统的影响，缺少详尽的理论推导以及相对应的实例分析。因此，研究5-UPS/PRPU冗余驱动并联机构的内力，并提出一种行之有效的降低内力的方法具有十分重要的理论价值和实践意义。

本文利用螺旋理论中的互易积原理[11]，推导出了5-UPS/PRPU冗余驱动并联机构的全雅可比矩阵，并且结合虚功原理以及伪逆法求解了5-UPS/PRPU冗余驱动并联机构的内力表达式。以对应的5-UPS/PRPU冗余驱动并联机床为例，分析了冗余分支驱动刚度的大小对其他各个分支内力幅值的影响，并提出了一种基于冗余驱动变刚度的协调内力的方法。该方法可以应用于冗余驱动控制、机械结构优化等方面的研究。

15-UPS/PRPU冗余驱动并联机构简介

5-UPS/PRPU五自由度冗余驱动并联机构(图1)由定平台、动平台以及连接定平台与动平台的六个驱动分支组成。该机构可以通过驱动五个结构完全相同的UPS分支中移动副的运动以及PRPU分支中第一个移动副的运动来实现动平台位姿的改变。此外，动平台绕其自身法线的转动自由度被PRPU分支所限制，因此该机构的自由度数为5。综上，由于驱动数目(6)大于其自由度数目(5)，因此可以将该机构描述为具有冗余驱动特征的5-UPS/PRPU五自由度冗余驱动并联机构，其中U表示虎克铰， P表示移动副(下划线表示驱动副)，S表示球副，R表示转动副。

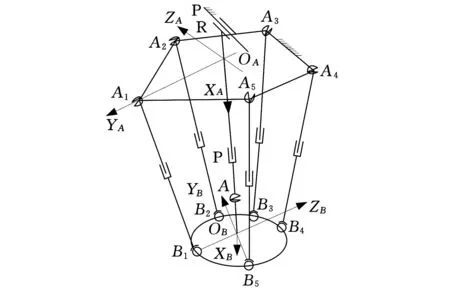
图1　5-UPS/PRPU机床结构简图

为了求解机构位置反解，将定坐标系{A}固定在定平台中心，将动坐标系{B}固定在动平台中心。如果将各个虎克铰的中心点表示为Ai(i=1,2,…,5)，其中A1位于坐标轴YA上，其余A2、A3、A4、A5则均布于以OA为圆心的圆周上。另外，若将各个球铰的中心点表示为Bi(i=1,2,…,5)，其各球铰中心点均布于以OB为圆心的圆周上，B1位于坐标轴ZB上。虎克铰中心Ai在定坐标系下的坐标表示为

其中，Ri为Ai到OA的距离，即半径；θi为Ri与YA轴的夹角；Hi为Ai在定坐标系中的X坐标；cθi表示cosθi,sθi表示sinθi。

动平台的各个球铰Bi在动坐标系{B}中的坐标可表示为

其中，ri为Bi到OB的距离，即半径；φi为ri与YB轴的夹角；hi为Bi在动坐标系中的X坐标。

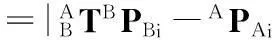
(1)

i=1,2,…,5

式中，li为各个驱动杆的杆长；APBi为球铰在定坐标系下的坐标。

2内力求解

2.1内力的幅值表达式求解

若假设已知动平台的速度，那么通过求解与该分支各个运动螺旋均互易的反螺旋便可求得该分支的约束力/力偶，由各个分支的约束力/力偶所组成的矩阵即为该机构的约束雅可比矩阵；另外，通过锁紧各个分支的驱动副，并求解该分支其余各个运动螺旋的反螺旋可以得到该分支的驱动力/力偶，由各个分支的驱动力/力偶所组成的矩阵即为该机构的驱动雅可比矩阵。本文中的5-UPS/PRPU冗余驱动并联机构的驱动/约束雅可比矩阵可以根据文献[11]得到：

(2)

(3)

(4)

联合式(2)~式(4),可得

(5)

式中，J为5-UPS/PRPU冗余驱动并联机构的全雅可比矩阵[12]。

根据雅可比矩阵的定义[13-14]可以得到，动平台的微位移与各个分支的变形一定满足以下关系：

JΔX=q

(6)

式中,ΔX为动平台由变形引起的微位移;q为各个分支的变形。

如果将J拆分成两部分,表示为

(7)

同样合并Δqna、Δqc:

(8)

由式(6)可得

JnacΔX=qnac

(9)

JraΔX=qra

(10)

显然,Jnac一定可逆。因此：

(11)

即为该5-UPS/PRPU冗余驱动并联机构的变形协调方程。其物理意义为机构冗余分支的变形与其余分支(非冗余分支与约束分支)变形间的协调关系。鉴于机构内力不对外做功的特点, 文献[15]将内力定义为“系统内在保持平衡时不对外作用的力”，那么在本文中内力被用来协调各个分支沿杆长方向的变形。

若将τna、τra、τc分别表示非冗余驱动力、冗余驱动力以及约束力螺旋的幅值,其大小可以根据下式进行计算：

(12)

其中,kna=diag(ka1,ka2,…,ka5),其对角线上的元素ka1,ka2,…,ka5表示各个UPS分支所对应的驱动刚度值;kra=[ka6],表示PRPU分支所对应的驱动刚度的大小;kc=[kc],表示PRPU分支所对应的约束刚度的大小;Δqna=[Δqa1Δqa2Δqa3Δqa4Δqa5]T表示由对应非冗余驱动力所引起的变形组成的列向量;Δqc=[Δqc]，表示由约束力矩所引起的变形；Δqra=[Δqa6]，表示由冗余驱动力所引起的变形。

联立式(11)和式(12),可得

(13)

(14)

其中，τ表示由各个分支驱动力组成的列向量,λ为一个可以任意选取的向量。

此外,如果机构动平台所受到的六维外力(外载、动平台的重力及其惯性力/力矩)为w,那么由动平台的受力平衡条件可得

(15)

其中

w=[FXFYFZMXMYMZ]T

τ=[τnaτraτc]T

式中，F、M分别为外力/力矩，下标X、Y、Z表示各个方向。

联立式(14)与式(15)可得

[FXFYFZMXMYMZ0]T=

(16)

对上式求逆,即可由分块矩阵求逆得

τ=J*[wT0]T

(17)

其中

式中,J*为式(16)中等号右侧矩阵的分块矩阵逆矩阵。

由式(17)可以发现，等式右侧最后一行恒为零，因此可以直接略去。该五自由度冗余驱动并联机构的驱动力螺旋与约束力螺旋的唯一解可以表示为

(18)

(19)

(20)

上述分析讨论的是假设机构刚度一定时，机构内力与其相应构型间的关系，然而，在实际生产应用中，机构的刚度(特别是机构驱动器所对应的驱动刚度)往往是变化的且需根据生产者的需求主动控制，因此，下一节将以5-UPS/PRPU冗余驱动并联机床为例，讨论机构的刚度变化对分支内力的影响。

2.2仿真验证

图2为5-UPS/PRPU冗余驱动并联机床在有限元软件中的简化模型。首先,计算各个驱动分支沿杆长方向的线刚度,将计算结果和表1中的机床参数代入式(20)进行计算，最终求得各个分支驱动力的大小。另一方面，在该有限元软件中加入简化后的机床模型，通过该软件中的StaticStructural模块对其进行静力分析，首先锁紧运动副，通过调用ForceReaction功能即可查看各个驱动分支的驱动力大小(如图2中箭头所示)。

图2　5-UPS/PRPU机床驱动力求解示意图

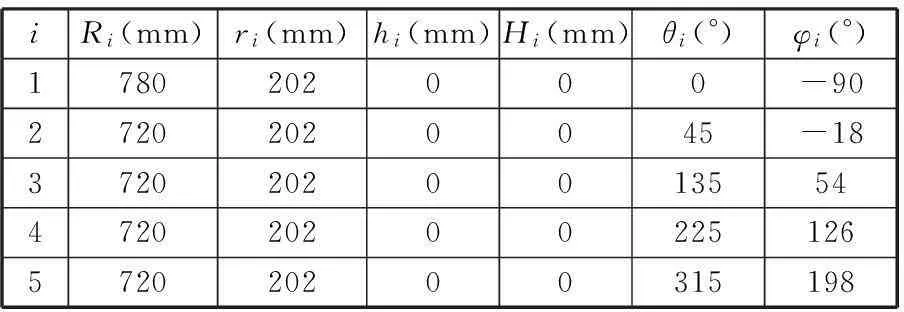
iRi(mm)ri(mm)hi(mm)Hi(mm)θi(°)φi(°)1780202000-9027202020045-1837202020013554472020200225126572020200315198

由于该机床的位姿不同，因此在有限元仿真软件中的结果会略有不同。由表2可知，位姿3对应的理论值与仿真结果差别较大，位姿1对应的理论值与仿真结果差别较小。造成该误差的原因可能是由于有限元软件中前处理(网格划分、接触设置等)的误差，以及等效模型(不规则质量块等)处理的误差等。通过比较机床不同位姿所对应的驱动力实际值与仿真结果可知，理论计算结果与有限元计算结果趋于一致，且其误差区间在3%~8%范围内，因此验证了前述分析方法的正确性。

表2　机床内力理论值与仿真值的误差

3驱动刚度对内力分布的影响内力求解

以5-UPS/PRPU冗余驱动并联机床为例，其结构如图3所示。需要注意的是，各个UPS 分支的驱动刚度在动平台运动过程中应该随其长度的变化而变化，但为了简化分析，这里我们认为UPS分支的驱动刚度均相同，即kai=2.3×107N/m(i=1,2,…,5)。同样地，假设冗余分支的约束刚度为kc=8.2×107N·m，5-UPS/PRPU冗余驱动并联机床主要结构参数如表1所示。

图3　5-UPS/PRPU机床模型结构图

根据式(19)对5-UPS/PRPU冗余驱动并联机构进行内力分析，观察其在运动过程中各个分支产生内力的幅值与冗余分支驱动刚度变化的关系。假设冗余分支(PRPU分支)的驱动刚度在1.97×107~2.03×107N/m内变化，其余非冗余驱动分支的驱动刚度不变(冗余分支的约束刚度也不变)，那么根据冗余驱动内力表达式式(20)可知，该机构的内力不仅与自身固有结构属性(即分支驱动/约束刚度)有关，其位置与姿态的变化也对其内力的幅值有着十分重要的影响。对于该5-UPS/PRPU冗余驱动并联机床而言，通过分析其工作空间内不同姿态下各分支内力的分布来了解其冗余分支的驱动刚度性能对系统内力的影响有着十分重要的意义，因此本文通过计算各个分支内力在动平台运动过程中随时间的变化以及冗余分支刚度的变化来说明驱动刚度对系统内力的影响。

图4~图9为机构各个分支对应的内力(内力矩)分布云图。通过分析可知,在动平台运动过程中,1号分支内力很小(最大值为1×10-3N),且冗余分支驱动刚度的变化对其分布几乎没有影响；2~5号分支的非冗余驱动力螺旋所对应的内力均随冗余分支驱动的刚度增加而降低，另外6号分支的约束螺旋所对应的内力矩同样随冗余分支驱动刚度的增加而降低。因此，我们可以得出结论：无论是驱动力螺旋还是约束力螺旋所对应的内力均随冗余驱动刚度的增大而减小。由此，在实际生产中工作人员可通过对冗余分支驱动刚度大小的控制降低其他分支的内力，也可以在机械系统设计初期通过提高驱动器机械刚度降低其他分支的内力，从而避免因内力过大产生的憋死甚至毁坏。然而，通过图10可知，冗余驱动力螺旋所对应的内力随其刚度的增大而增大。因此，鉴于对冗余分支结构的保护，不能因协调其他分支内力从而无限度地增大冗余分支的驱动刚度。此外，通过观察图4~图10，各个分支内力幅值的变化与时间变化的对应关系与各个分支杆长变化趋势一致，因此可以在一定程度上说明该方法的有效性。

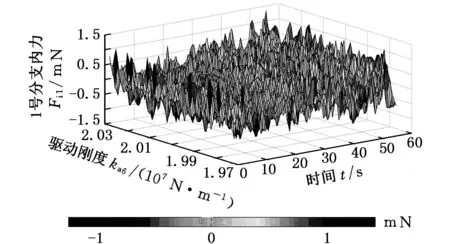
图4　1号分支对应的内力分布云图

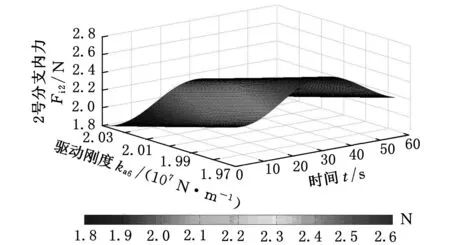
图5　2号分支对应的内力分布云图

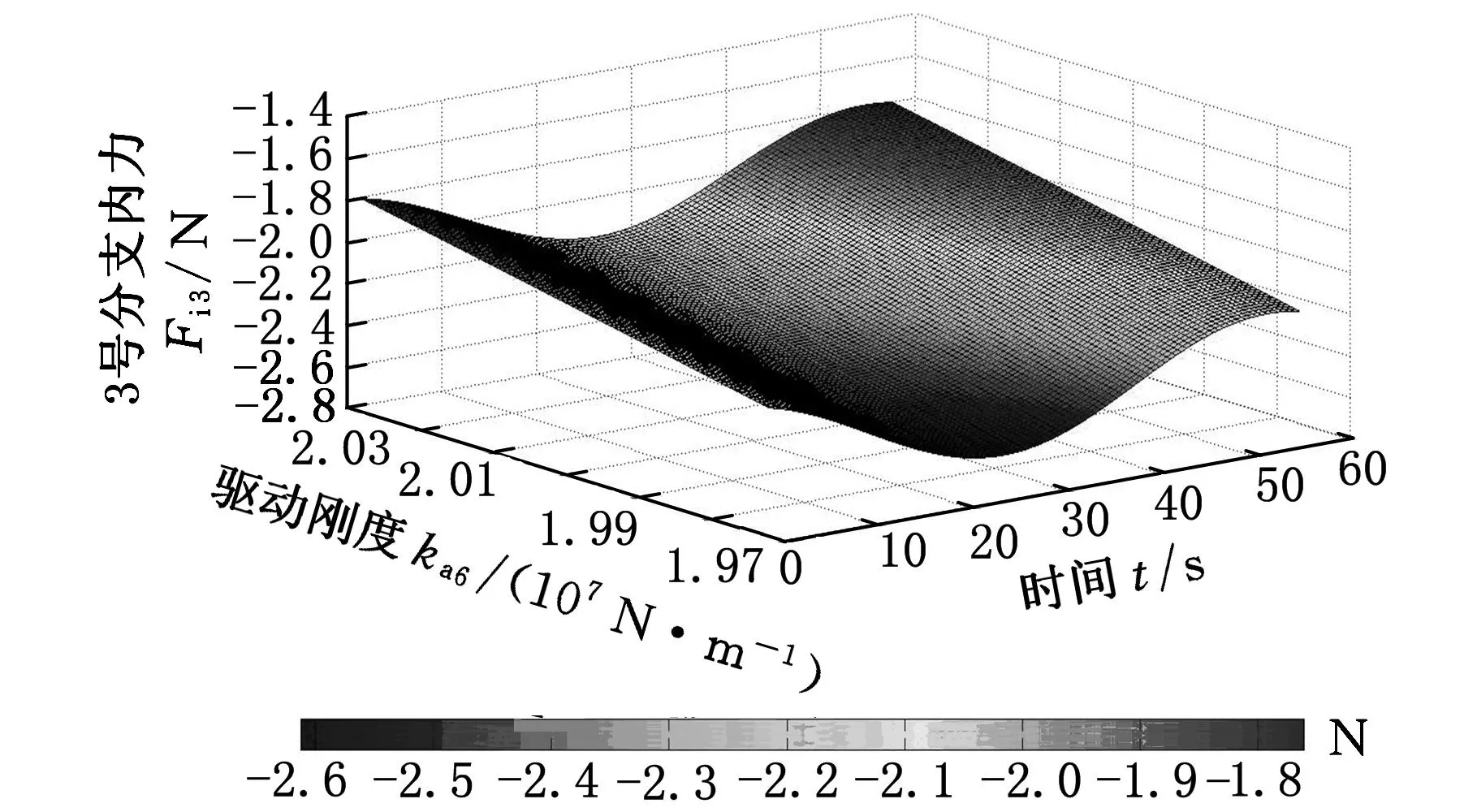
图6　3号分支对应的内力分布云图

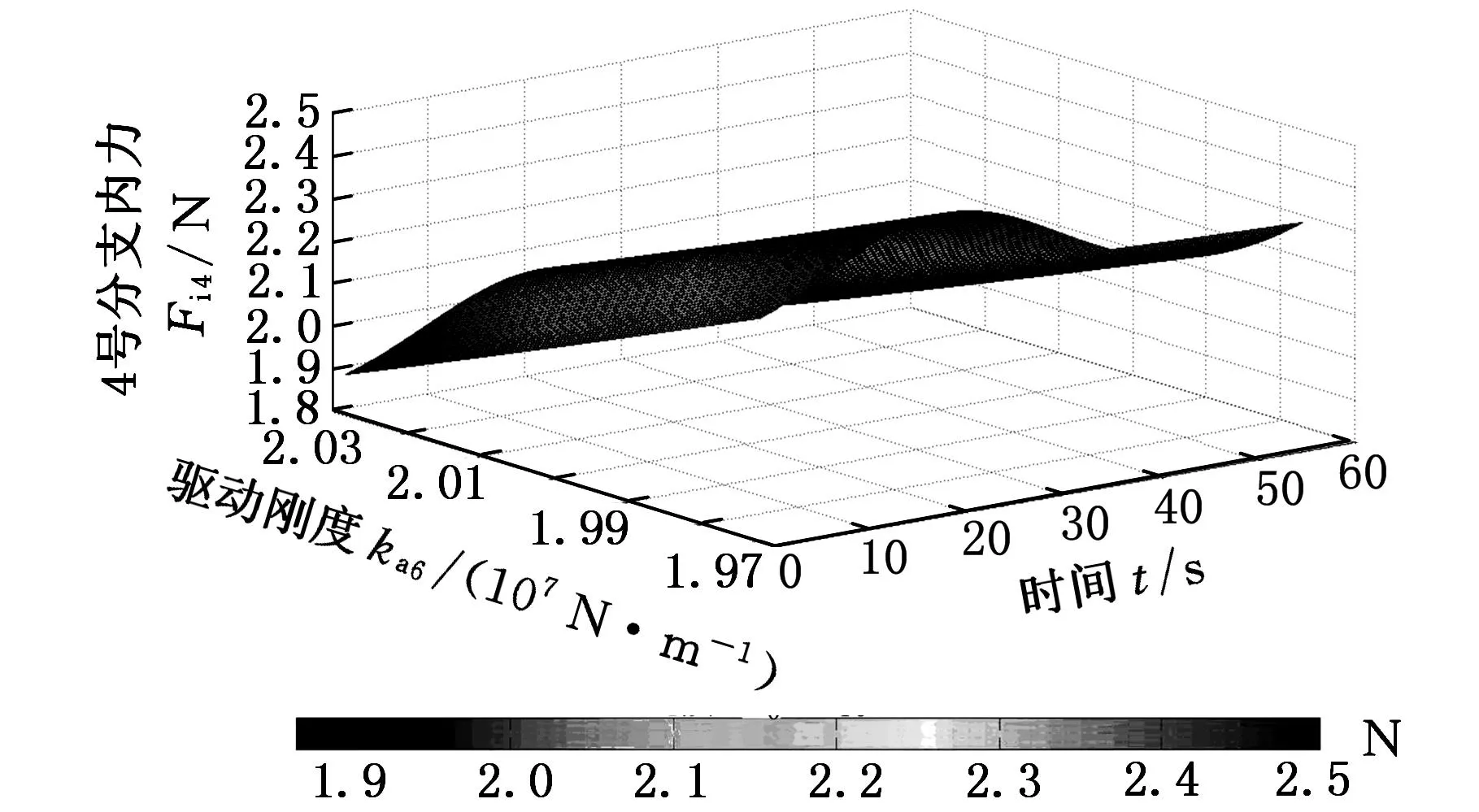
图7　4号分支对应的内力分布云图

图8　5号分支对应的内力分布云图

图9　6号分支对应的内力矩分布云图

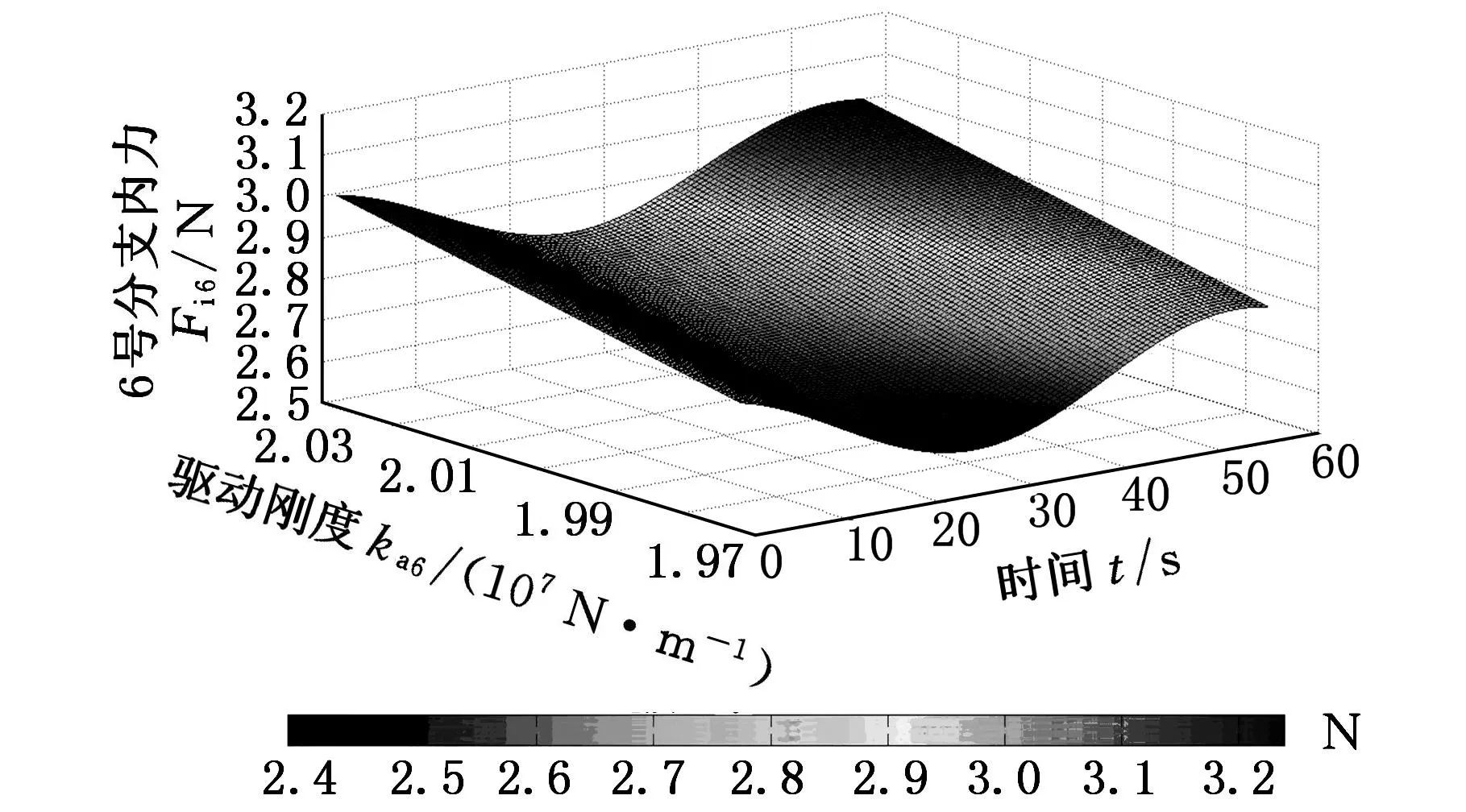
图10　6号分支对应的内力分布云图

4结论

(1)本文利用机构全雅可比理论推导了5-UPS/PRPU冗余驱动并联机构的变形协调方程，并通过使用伪逆法求解机构全雅可比矩阵关于刚度的加权广义逆，从而求解出机构的内力，并通过有限元仿真软件验证了该方法的有效性。

(2)以5-UPS/PRPU冗余驱动并联机床作为算例,得到了其各个分支的内力幅值在对应运动空间内随冗余驱动刚度变化的关系。

(3)分析结果表明：通过合理调整冗余驱动刚度的大小可以在一定范围内降低其余分支的内力幅值。该方法既可以应用到冗余驱动控制算法中，即通过调节驱动伺服刚度协调各个分支内力，也可应用到机械系统前期设计中，即通过改善驱动器及其传动部件的机械刚度降低其他分支内力。

参考文献:

[1]Cheng H,Liu F G,Yiu Y K,et al.Advantages and Dynamics of Parallel Manipulators with Redundant Actuation[C]//Proceeding of the 2001 IEEE/RSJ International Conference on Robotics and Systems.Maui,Hawaii,USA,2001:171-176.

[2]杨钢，傅晓云，李宝仁.两自由度冗余驱动并联机器的研究[J]. 系统仿真学报，2006，18(2)：416-419.

Yang Gang,Fu Xiaoyun,Li Baoren.Research on 2-DOF Parallel Manipulator with Redundant Actuation[J].Journal of System Simulation,2006,18(2)：416-419.

[3]Gosselin C, Angeles J.Singularity Analysis of Closed Loop Kinematic Chains[J]．IEEE Transaction on Robotics and Automation，1990，6(3) : 281-290．

[4]Zhao Y J, Gao F, Dong X J, et al. Elastodynamic Characteristics Comparison of the 8-PSS Redundant Parallel Manipulator and Its Non-redundant Counterpart-the 6-PSS Parallel Manipulator[J]. Mechanism and Machine Theory,2010,45(2):291-303.

[5]窦玉超,姚建涛,赵永生,等.冗余驱动并联机器人动力学建模与驱动力协调分配[J]. 农业机械学报，2014,45(1):293-299.

Dou Yuchao, Yao Jiantao, Zhao Yongsheng, et al. Dynamic Modeling and Driving Force Coordinate Distribution of the Parallel Robot with Redundant Actuation[J]. Transactions of the Chinese Society for Agricultural Machinery,2014,45(1):293-299．

[6]Marquet F,Krut S,Company O,et al. ARCHI: a New Redundant Parallel Mechanism-modeling, Control and First Results[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems.Maui,Hawaii,2001,1:183-188.

[7]白志富,梁辉,陈五一.冗余并联机构的内力及应用[J]. 机械设计与研究, 2006, 22(4):13-17.

Bai Zhifu, Liang Hui, Chen Wuyi. Internal Forces of Parallel Mechanisms: Theory and Application[J]. Machine Design and Research, 2006, 22(4):13-17.

[8]Xu Y D,Yao J T,Zhao Y S.Inverse Dynamics and Internal Forces of the Redundantly Actuated Parallel Manipulators[J].Mechanism and Machine Theory,2012,51:172-184.

[9]何景峰，李保平，佟志忠,等. 液压驱动冗余振动台自由度控制及内力协调[J]. 振动与冲击,2011,30(3):74-78.

He Jingfeng,Li Baoping,Tong Zhizhong,et al.DOF Control and Inner Force Balancing of Hydraulically Redundant Actuated Shaking Table[J].Journal of Vibration and Shock,2011,30(3):74-78.

[10]梁辉,陈五一.一种靠内力提高并联机构精度的方法的研究[J].组合机床与自动化技术,2009(5):49-51.

Liang Hui,Chen Wuyi.Method of Improving Accuracy of Parallel Machine Tools by Internal Force[J].Modular Machine Tool & Automatic Manufacturing Technique,2009(5):49-51.

[11]黄真,赵永生,赵铁石.高等空间机构学[M].北京:高等教育出版社,2006.

[12]周鑫，许允斗，姚建涛,等. 5-UPS/PRPU冗余驱动并联机床完整刚度模型及其刚度特性[J]. 光学精密工程，2015,23(4):1070-1080.

Zhou Xin,Xu Yundou,Yao Jiantao,et al.Complete Stiffness Model and Stiffness Performance of 5-UPS/PRPU Redundantly Actuated Parallel Machine Tool[J].Optics and Precision Engineering,2015,23(4):1070-1080.

[13]Li Y M,Xu Q S.Stiffness Analysis for a 3-PUU Parallel Kinematic Machine[J].Mechanism and Machine Theory,2008,43(2):186-200

[14]Wang Y Y, Liu H T, Huang T, et al. Stiffness Modeling of the Tricept Robot Using the Overall Jacobian Matrix[J]. Journal of Mechanisms and Robotics,2009,1(1):795-810.

[15]Hanafusa H,Adli M A.Effect of Internal Forces on Stiffness of Closed Mechanisms[C]//15th International Conference on Advanced Robotics in Unstructured Environments.Pisa,1991,1:845-850.

(编辑王旻玥)

Internal Force Analysis and Coordination of a 5-UPS/PRPU Redundantly Actuated Parallel Mechanism

Zhou Xin1,2Xu Yundou1,2Yao Jiantao1,2Zheng Kuijing1,2Zhao Yongsheng1,2

1.Parallel Robot and Mechatronic System Laboratory of Hebei Province,Yanshan University,Qinhuangdao,Hebei,066004 2.Key Laboratory of Advanced Forging & Stamping Technology and Science of Ministry of National Education,Yanshan University,Qinhuangdao,Hebei,066004

Abstract:By combining the overall Jacobin matrix and pseudo-inverse matrix method, the internal forces of each driving limb of a 5-UPS/PRPU redundantly actuated parallel mechanism were derived,and a novel internal force coordination method was presented.By using compatibility equation of deformation, the pseudo-inverse of the overall Jacobian of the mechanism could be obtained.The internal forces of the 5-UPS/PRPU parallel mechanism were solved as well,which was verified by finite element method.To investigate the influences of stiffness of the redundant actuator on the internal forces of each driving limb,the 5-UPS/PRPU redundantly actuated parallel machine tool(PMT) was used to illustrate the method mentioned above,and a method to coordinate internal forces was proposed.The analyses show that the actuation wrench of the non-redundant limb and the constraint wrench of the redundant limb can be reduced by increasing the stiffness of the redundant actuator to some extent. The method may be used by mechanism designer and programmer to improve the systems precision and reduce the internal forces of the mechanisms.

Key words:parallel mechanisms;redundant actuation;variable stiffness;internal force

作者简介：周鑫, 男，1988年生。燕山大学机械工程学院博士研究生。主要研究方向为机构学、机器人技术及应用等。许允斗,男,1985年生。燕山大学机械工程学院讲师。姚建涛,男,1980年生。燕山大学机械工程学院副教授。郑魁敬,男,1971年生。燕山大学机械工程学院副教授。赵永生(通信作者),男,1962年生。燕山大学机械工程学院教授、博士研究生导师。

中图分类号：TP394.1；TH691.9

DOI：10.3969/j.issn.1004-132X.2016.06.001

基金项目：国家自然科学基金资助项目(51275439);燕山大学青年教师自主研究计划课题(13LGA001)

收稿日期：2015-07-21