结构力学求解器在力学与结构中应用探讨

郑元锋

（福建水利电力职业技术学院，福建 永安，366000）

1 引言

结构力学求解器[1]是一个面向教师、学生及工程技术人员的结构计算分析软件。软件包括编辑器与观览器两个窗口，其界面简洁，操作方便。该软件具有建模快速、直观，求解显示准确、美观等特点。在建筑力学与建筑结构中，常用结构力学求解器[2]来解决力学与结构问题，

本文探讨结构力学求解器在应用中遇到的一些问题，以及如何应用结构力学求解器快速求解建筑力学与建筑结构中常用结构[3]的内力系数。为叙述方便，下面将“结构力学求解器”简称为“求解器”。

2 求解器求解结构内力的步骤

应用求解器绘制（或求解）结构内力图（或截面内力）分两步：第一步，建立结构模型；第二步，求解显示内力图（或截面内力）。

结构建模步骤：定义结点→定义单元→位移约束→荷载条件→材料性质（超静定结构计算时）。

内力图显示步骤：求解→内力计算→内力显示。

3 求解器在建筑力学中应用探讨

下面通过一些实例，来探讨求解器在建筑力学内力计算中的应用。

3.1 拱的内力计算

拱属于曲杆，拱截面内力计算复杂，手工计算绘制拱的内力图更是一个庞大而烦琐的工程。采用求解器计算拱内力[4]，目前也只是近似计算，其方法是采用分段的直杆近似代替拱（曲杆）。如何提高求解器计算拱内力的相对精度？其要点：一是适当增加拱的分段数；二是拱上有集中荷载、集中力偶或分布荷载的两端点必须是分段点。下面是同一拱结构，通过两种不同分段数来比较拱的内力（轴力、剪力与弯矩）。

实例一：试绘制图1 所示三铰拱的内力图，并求D 截面的内力。拱轴为二次抛物线，其拱轴线方程为。拱上荷载q=2k N/m，F=6kN。

图1 三铰拱

下面应用求解器[1]建立上述三铰拱模型并显示内力图。

情况一：拱跨沿水平方向（x 向）等分为八段。图中1，2……9 为分段节点号，拱的内力图如下图2、图3、图4 所示。

图2 拱轴力图——图（kN）

图3 拱剪力图——图（kN）

图4 拱弯矩图——图（kN·m）

情况二：拱跨沿水平方向（x 向）等分为十六段。图中1，2……17 为分段节点号，拱的内力图如下图5、图6、图7 所示。

图5 拱轴力图——图（kN）

图6 拱剪力图——图（kN）

图7 拱弯矩图——

图（kN·m）

应用求解器求得拱D 截面内力值如下：

情况一：

情况二：

比较上述两种不同分段拱的内力图可知：当拱的分段数越多时，其内力值越接近拱内力精确值；拱的分段数对拱的剪力影响更大。

3.2 采用符号表示的结构内力计算

在建筑力学或建筑结构中，常遇到用符号表示杆件长度与荷载的结构计算简图，应用求解器又该如何绘制或计算结构内力图？下面通过实例二来说明。

实例二：试绘制图8 所示结构的内力图（剪力图与弯矩图）。

图8 实例二计算简图

实例二采用求解器建模[5]时，其方法是：

取a=1，q=1，则杆件长度取2a=2，4a=4，a=1；荷载取q=1，3qa=3，2qa2=2。

绘制（显示）内力时，杆件实际内力值为：

剪力实际值为计算值*qa（即V实=V计*qa）。

弯矩实际值为计算值*qa2（M 实=M计*qa2）。实例二采用求解器显示其内力图如图9、图10 所示。

图9 剪力图——图（*qa）

图10 弯矩图——图（*qa2）

对于以下实例三（图11），若未知长度a 与b，荷载q 与F、m1之间的具体比例关系，则无法应用求解器建立结构模型，当然也无法计算内力或绘制内力图。

图11 实例三计算简图

3.3 单跨超静定结构系数计算

在建筑力学[6]或工程力学[7]中，采用位移法或力矩分配法计算超静定结构的内力时，须用到“等截面单跨超静定梁的形常数和载常数”（杆端弯矩与杆端剪力），计算时通常直接查表使用。对表中的数值（杆端弯矩与杆端剪力），也可采用求解器计算所得。

下面选择表[7]中两个实例，采用求解器来验证表中的数值。习惯将梁因单位位移引起的端内力称为形常数；将梁因荷载引起的端内力称为载常数。

（1）形常数求解

实例四（图12）：两端固定的AB 杆件在A 端发生单位转角（φA=1），杆件长为l，抗弯刚度为EI，求杆端弯矩值（MAB与MBA）及杆端剪力值（VAB与VBA）。

图12 实例四结构计算简图

采用求解器建立结构模型时，其方法是：

求解→内力计算→内力显示，得到以下剪力图（图13）与弯矩图（图14）。

图13 剪力图--图（*EI/l2）

图14 弯矩图--图（*EI/l）

根据杆端内力正负号规定：杆端弯矩以顺时针转向为正，逆时针转向为负；杆端剪力以使杆件顺时针转动趋势为正，反之为负。从图14 弯矩图与图13 剪力图可知：

（2）载常数求解

图15 实例五结构计算简图

采用求解器建立结构模型时，其方法是：

求解→内力计算→内力显示，得到以下剪力图（图16）与弯矩图（图17）。

图16 剪力图——图（*ql）

图17 弯矩图——图（）

在上面的剪力图与弯矩图中，求解器软件只显示到小数点后两位数值，更准确的数值可通过内力计算中“杆端内力值”或“单元内力分析”计算，如下图18 所示。

图18 杆端内力值

根据图18，可知：

（四）构件内力图显示问题

实例六：如图19 等截面三跨连续梁，每跨作用有两个集中荷载，试绘制其剪力图。

图19 三跨连续梁

采用求解器建立图19 三跨连续梁模型。

求解→内力计算→内力显示，得到以下剪力图（图20）。

图20 剪力图——图

从图20 剪力图可知，该连续梁在中间跨的剪力图显示不正确。中间跨在集中荷载作用处剪力应该是垂直突变的，但上面剪力图显示的是斜线渐变，其错误原因是求解器软件对杆件（单元）内力图显示，默认划分段数为10 段而造成的。当以上中间跨的分段点不在集中荷载作用时，这时显示的构件剪力图就不正确。如何正确地显示以上构件剪力图？采用的办法是增加构件内力图的分段数，具体操作步骤是“观察器→设置→选项→划分段数”。当构件内力图划分为50 段时，其剪力图如下图21 所示：

图21 剪力图——（划分为50 段时）

4 求解器在建筑结构中应用

4.1 连续梁的内力系数

在各类《混凝土结构》[8]或《混凝土结构与砌体结构》[9]的附录表中，通常都附有“均布荷载和集中荷载作用下等跨连续梁的内力系数表”，对附表中的数值，多数使用者只懂得查表计算，不知表中数值如何得到，更不关心表中数值是否正确。

下面以集中荷载作用下四跨连续梁为例，讲解如何应用求解器快速计算附表[8-9]中内力系数值。

图22 四跨连续梁（集中荷载）

实例七：试确定上图22 集中荷载作用下四跨连续梁的内力系数（弯矩系数与剪力系数）。

附表[9]中上图四跨连续梁的内力计算公式：应用求解器建立四跨连续梁模型时，其方法是：取，集中荷载 作用在每跨三分点处。计算分析：当时，则1=k1，V=k2P=k2×1=k2

以上计算可知，此时弯矩图与剪力图中对应截面的弯矩值与剪力值就是相应的内力系数k1与k2值。

以下为求解器显示的剪力图（图23）与弯矩图（图24）

图23 四跨连续梁剪力图——图

图24 四跨连续梁剪力图——图

在上面的剪力图与弯矩图中，软件只显示到小数点后两位数值，更精确的数值如下图25 所示。

图25 四跨连续梁杆端内力值

杆件跨中截面的内力值可通过上图25 中“单元内力分析”选择“单元”与“距杆端1”的1/3 或2/3 处显示，最后得到集中荷载作用下四跨连续梁内力系数如下表1 所示。

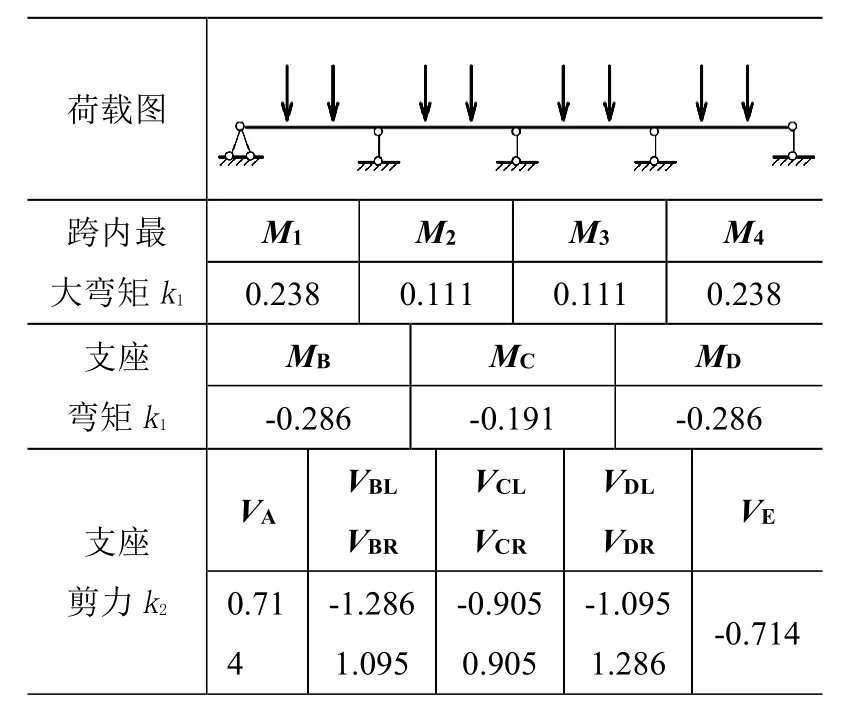
表1 集中荷载作用下等跨连续梁内力系数表（四跨）

（二）框架结构内力计算

图26 实例八框架结构

在框架结构[10]内力计算中，其杆件抗弯刚度只需相对值即可。本例应用求解器建模时，重点是确定杆件的抗弯刚度相对值即可）。由杆件线刚度定义（），可求出杆件的抗弯刚度（），即杆件与杆件的抗弯刚度（相对值），杆件的抗弯刚度（相对值）。

实例八应用求解器建模程序如下：

TITLE,框架结构内力计算

结点,1,0,0

结点,2,0,6

结点,3,12,6

结点,4,12,0

单元,1,2,1,1,1,1,1,1

单元,2,3,1,1,1,1,1,1

单元,3,4,1,1,1,1,1,1

结点支承,1,6,0,0,0,0

结点支承,4,6,0,0,0,0

单元荷载,1,3,4,0,1,90

单元材料性质,1,1,-1,6,0,0,-1

单元材料性质,2,2,-1,14.4,0,0,-1

单元材料性质,3,3,-1,6,0,0,-1

END

实例八框架结构的内力图如下：

图27 轴力图——图（kN）

图28 剪力图——图（kN）

图29 弯矩图——图（kN·m）

5 结语

本文从具体实例入手，一是探讨了结构力学求解器在结构内力计算或绘制中遇到的一些问题，以及如何较好地解决这些问题；二是探讨了如何应用结构力学求解器计算建筑力学与建筑结构中各类系数（形常数、载常数、连续梁内力系数）。