灰色神经网络组合模型预测沉降数据

余露

摘要：采用灰色模型、BP神经网络模型以及两者联合的数据处理模型对港口防波堤的沉降进行数据处理和预测处理；通过灰色系统与BP神经网络联合模型与各自单独的模型对比分析，两者的联合模型在港口防波堤的沉降预测中有更高的可靠性。

关键词：港口防波堤；沉降预测；灰色模型；BP神经网络

一、绪论

防波堤为阻断波浪的冲击力、围护港池、维持水面平稳以保护港口免受坏天气影响、以便船舶安全停泊和作业而修建的水中建筑物[1]。

由于防波堤砌体重量较大可达上100吨，再加上海浪以及由于海底的淤泥和沙质地质的综合影响，那么整个港口的防波堤在安装建设的过程中以及建成过后都会发生沉降，而且在实际交付使用的时候要求防波堤的堤顶高程要高于设定的高程才能安全的有效的防止海浪和有效的保护港口内的船只。

二、灰色模型与BP神经网络模型

防波堤的沉降影响因素不仅受堤体自重、海浪、海底地质等因素的影响，而且受其他的因素的影响；如：潮汐、日月引力、固体潮等因素的影响，这些参数在实际中有些无法测量或者实际应用中的精度没有考虑这些因素。这就导致影响因素的灰色性同时因为多影响因素所以可以采用神经网络模型灰色系统理论是由华中理工大学邓聚龙教授于1982年创立并发展起来的[2]。

BP神经网络属前向网络，但它采用的是反向传播的学习方法。BP网络是对非线性可微分函数进行权值训练的多层网络，主要用于函数逼近、模式识别、分类及数据压缩等[3]。

三、GM（1，1）处理沉降数据

以其中一点如C4点的沉降数据为例进行处理预测，共11期沉降数据，以前八期的数据作为灰色模型的原始序列然后对后三期的数据进行预测验证。

1、原始序列x（0）（k）=（x（0）（1），x（0）（2），x（0）（3），…，x（0）（n））进行一次累加生成处理得到x（1）（k）=（x（1）（1），x（1）（2），x（1）（3），…，x（1）（n））。其中的累加内核公式为：

x（1）（k）=∑ki=1x（0）（i），k=1，2，3…，n（3.1）

2、计算得出均值序列即对累加生成的序列x（1）（k）进行均值生成：Z（1）（k）=12[x（1）（k-1）+x（1）（k）]，k=2，3，…，n（3.1）

3、得到灰色模型的时间响应函数：

（1）（k+1）=（x（0）（1）-ba）e-ak+ba（3.3）

3.得到最终的响应式：

（0）（k+1）=（1-ea）（x（0）（1）-ba）e-ak（3.2）

4、采用最小二乘法计算a、b的估计值，这样可以得到最优的估计值，

通过计算得到=[a，b]T的最佳估计值。

5、由累减生成方法还原原始序列：（0）（k）=（1）（k）-（1）（k+1）；上述步骤可以通过matlab程序就可以得到前八期的模拟值以及向后预测三期的预测数据。采用均方差比值D来验证精度，D=S2/S1其中：后验方差比值D就为：误差的标准差与原始序列标准差的比值。

D=S2=1n∑nk=1E（K）-2S1=1n∑nk=1x（0）（k）-2（3.7）

得到D=02417，D小于精度标准的035，模型的精度为良好。

四、采用BP神经网络处理数据

在预测之前，为了数据处理更加方便快捷，需要将原始数据进行归一化处理。确定神经网络的结构模型，输入层为三个节点，输出层有一个节点，通过公式m+n+a，m为输入层节点数，n为输出层节点数a属于[1，10]之间的数，确定隐含层的节点数这里取四。用前8期数据作为输入样本，第九期、第十期和第十一期进行预测验证。

构建神经网络预测模型的核心思想可以概括为：第1、2、3期预测第四期第2、3、4期预测第五期，依次类推前八期为训练数据，后三期为预测数据。通过程序的计算得出整体的均方误差MSE为21773；误差相当大。主要是由于后三个预测值的影响。

五、GM（1，1）与BP神经网络联合

灰色模型具有良好的兼容性可以和其他算法模型进行兼容，同时神经网络模型本身也具有灰色性，所以两者可以进行联合的处理数据[4]。同时通过以上的灰色模型和BP神经网络模型对同一组数据的处理可以看出，两个算法在模拟计算时精度较高，但是在预测时误差就特别大。

采用BP神经网络的方法对灰色模型处理的模拟的预测值的残差结果进行模拟和处理，即对残差数据进行处理，然后得到残差的处理值，根据（0）（i）=（0）（i）+（0）（i），i=1，2，…，n得出最終的模拟值和预测值。

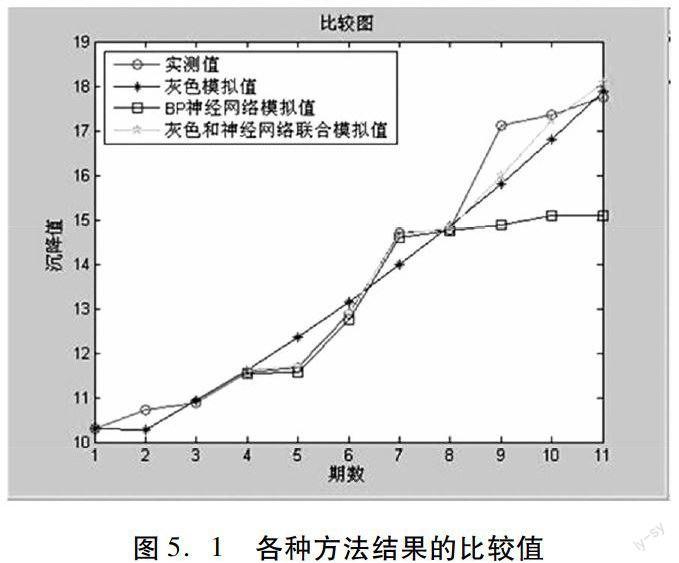
通过matlab绘制灰色模型模拟值、BP神经网络模拟值、灰色模型与神经网络联合处理的模拟值的图形进比较：

六、结论

通过比较分析可以看出在本次沉降数据处理中，由于BP神经网络对数据量的要求较高，所以导致在模拟时有较高的精度但是在预测时精度较差，而灰色模型把原本不具备规律的数据进行处理在模拟和预测时精度较高可以应用于本次数据处理；灰色模型与BP神经网络的联合处理所得到的结果无论在模拟还是在预测方面都是与实测值最相近的，所以灰色模型和BP神经网络模型的联合模型可以良好的应用于本次防波堤的数据处理之中。

参考文献：

[1]宫云增，阚卫明.天津港北大防波堤工程半圆体沉降观测和初步分析[J].中国港湾建设，2003

[2]邓聚龙.灰理论基础[M].武汉：华中科技大学出版社，2002

[3]邓聚龙.灰色系统基本方法[M].武汉：华中理工大学出版社，1987

[4]付海兵，曾黄麟.BP神经网络的算法及改进[J].中国西部科技，2012，11（8）.23～24

[4]田秀梅.BP算法的改进及仿真研究[J].电子技术研发：64～66

[5]谢中华，李国栋等matlab从零到进阶[M].北京航空航天大学出版社，2012