线性测量误差模型的随机加权分位数回归

刘　莹， 葛悠美， 姜　荣

(东华大学 理学院， 上海 201620)



线性测量误差模型的随机加权分位数回归

刘莹， 葛悠美， 姜荣

(东华大学 理学院， 上海 201620)

摘要：将随机加权法推广到线性测量误差模型，结合分位数回归估计方法，提出线性测量误差模型中参数的随机加权分位数回归方法.在一定条件下，可以用随机加权法得到分位数回归估计量的渐近分布，这种方法避免了估计冗余参数，并且实施方便.通过模拟研究和艾滋病数据验证了随机加权分位数回归方法的有效性.

关键词：测量误差； 分位数回归； 随机加权方法

考虑如下线性测量误差模型[1]：

(1)

其中：x∈Rp是存在测量误差的未观测的随机变量；X∈Rp是x的观测值；β是p维未知参数向量；Y∈Rp是响应向量；(ε， uT)T∈Rp+1是期望为零且独立同分布的.设x是独立同分布的随机变量.x是非随机的情况参见文献[2].模型(1)作为线性测量误差模型，修正了由于自变量测量误差的引入所导致的参数估计的偏差，在某一程度上比普通的线性回归

模型更加实用.

由于分位数回归方法不仅能够度量回归变量对分布中心的影响，而且能度量回归变量对分布上尾和下尾的影响，因此，其比经典的最小二乘回归法更具有优势.分位数回归已在很多领域得到应用，如经济学[3-4]、生存分析[5-6]、生长曲线图[7-8]及其他[9-11].文献[12]考虑了线性和部分线性测量误差模型的分位数回归估计，并建立了相应的渐近性质.然而由于估计量的渐近分布中存在冗余参数，很难被精确地估计.随机加权法可以有效地解决上述问题.

随机加权法[13]可以看作Bootstrap方法[14]的一个变形，它不是从数据中产生重复样本，而是在每个观察数据前附加一个随机权，通过重加权产生再生样本来模拟总体分布(取再生样本的容量和观测样本一样).文献[15]研究表明，随机加权方法和 Bootstrap 方法有相似的渐近性质(至少在一阶时).由于随机加权法具有良好的统计特性，在统计的某些方面已经对其做了广泛的研究.例如，文献[15]使用随机加权法得到线性回归模型中 M 估计的近似分布；文献[16]提出了比例风险模型的随机加权法；文献[17]将随机加权法拓展到了删失回归模型；文献[18]讨论了半线性测量误差模型中的未知参数的随机加权最小二乘估计.但文献中很少有通过随机加权法研究模型(1).

本文将随机加权法应用于模型(1)，提出用于线性测量误差模型的随机加权分位数回归方法，并给出相应的渐近性质，最后通过模拟以及实例研究，验证随机加权分位数回归方法的有效性.

1方法和主要结果

1.1随机加权分位数回归

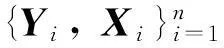
(2)

其中：ρτ(r)=τr-rI(r<0)，r为变量，τ为分位数，I(·)为示性函数.此外，文献[12]证明在一定条件下，有

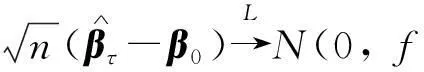
(3)

S=τ(1-τ)Σx+

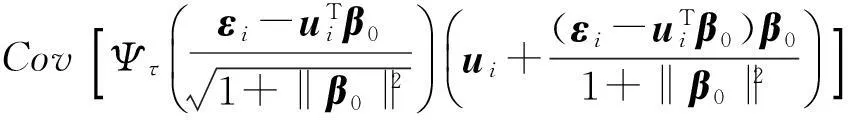
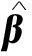
(4)

其中：随机权ωi(i=1， 2， …， n)是独立同分布且E(ω1) =Var(ω1)=1的非负随机变量.

研究估计量的渐进性质，需要以下条件.

A1设(ε， uT)球对称，且存在有限一阶矩.ε的分布函数F绝对连续，密度函数f在点qτ连续，且从0到∞一致有界.

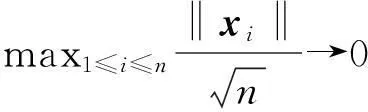
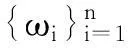
注：条件A1和A2是分位数回归的常见条件[8]，条件A3常用于随机加权法[16].

(5)

特别，当ωi=1，有

(6)

定理2在定理1的条件下，有

op(1)

相应地，

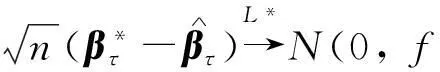
(7)

2模拟结果

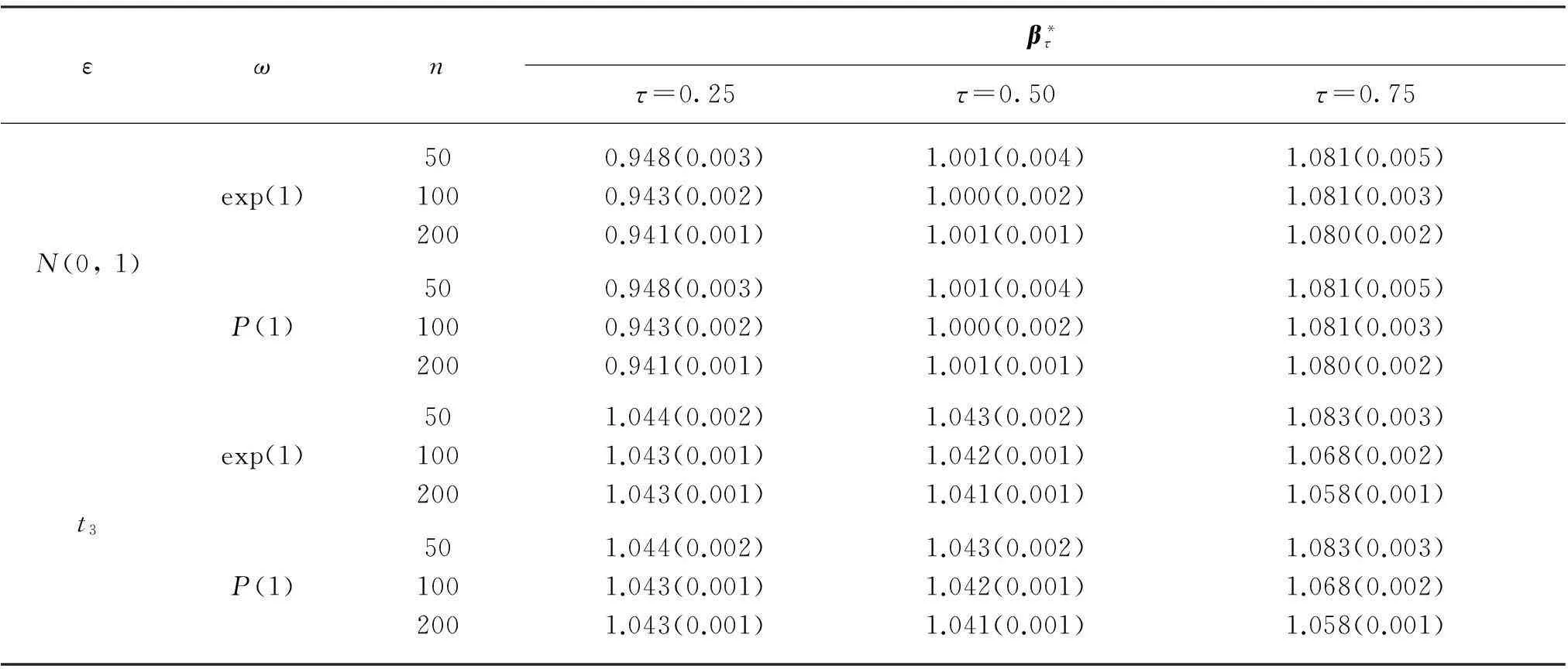
例1模拟数据由模型(1)生成，且随机误差变量分别服从标准正态分布N(0， 1)和自由度为3的t分布t3.自变量x是区间(3， 5)生成的均匀分布，研究β=1，2和5这3种情况.随机加权变量ω分别

服从均值为1的指数分布exp(1)和均值为1的泊松分布P(1).所有的模拟重复运行 500次，随机加权数重复次数为500.

εωnβ*ττ=0.25τ=0.50τ=0.75N(0,1)500.948(0.003)1.001(0.004)1.081(0.005)exp(1)1000.943(0.002)1.000(0.002)1.081(0.003)2000.941(0.001)1.001(0.001)1.080(0.002)500.948(0.003)1.001(0.004)1.081(0.005)P(1)1000.943(0.002)1.000(0.002)1.081(0.003)2000.941(0.001)1.001(0.001)1.080(0.002)t3501.044(0.002)1.043(0.002)1.083(0.003)exp(1)1001.043(0.001)1.042(0.001)1.068(0.002)2001.043(0.001)1.041(0.001)1.058(0.001)501.044(0.002)1.043(0.002)1.083(0.003)P(1)1001.043(0.001)1.042(0.001)1.068(0.002)2001.043(0.001)1.041(0.001)1.058(0.001)

εωnβ*ττ=0.25τ=0.50τ=0.75N(0,1)501.828(0.007)2.008(0.008)2.248(0.016)exp(1)1001.818(0.004)2.003(0.005)2.255(0.008)2001.824(0.002)2.004(0.002)2.240(0.005)501.828(0.007)2.008(0.008)2.248(0.016)P(1)1001.818(0.004)2.003(0.005)2.255(0.008)2001.824(0.002)2.002(0.002)2.240(0.005)t3502.035(0.002)2.036(0.002)2.055(0.006)exp(1)1002.034(0.001)2.034(0.001)2.045(0.002)2002.035(0.001)2.032(0.001)2.043(0.001)502.035(0.002)2.036(0.002)2.054(0.005)P(1)1002.034(0.001)2.034(0.001)2.045(0.002)2002.035(0.001)2.032(0.001)2.043(0.001)

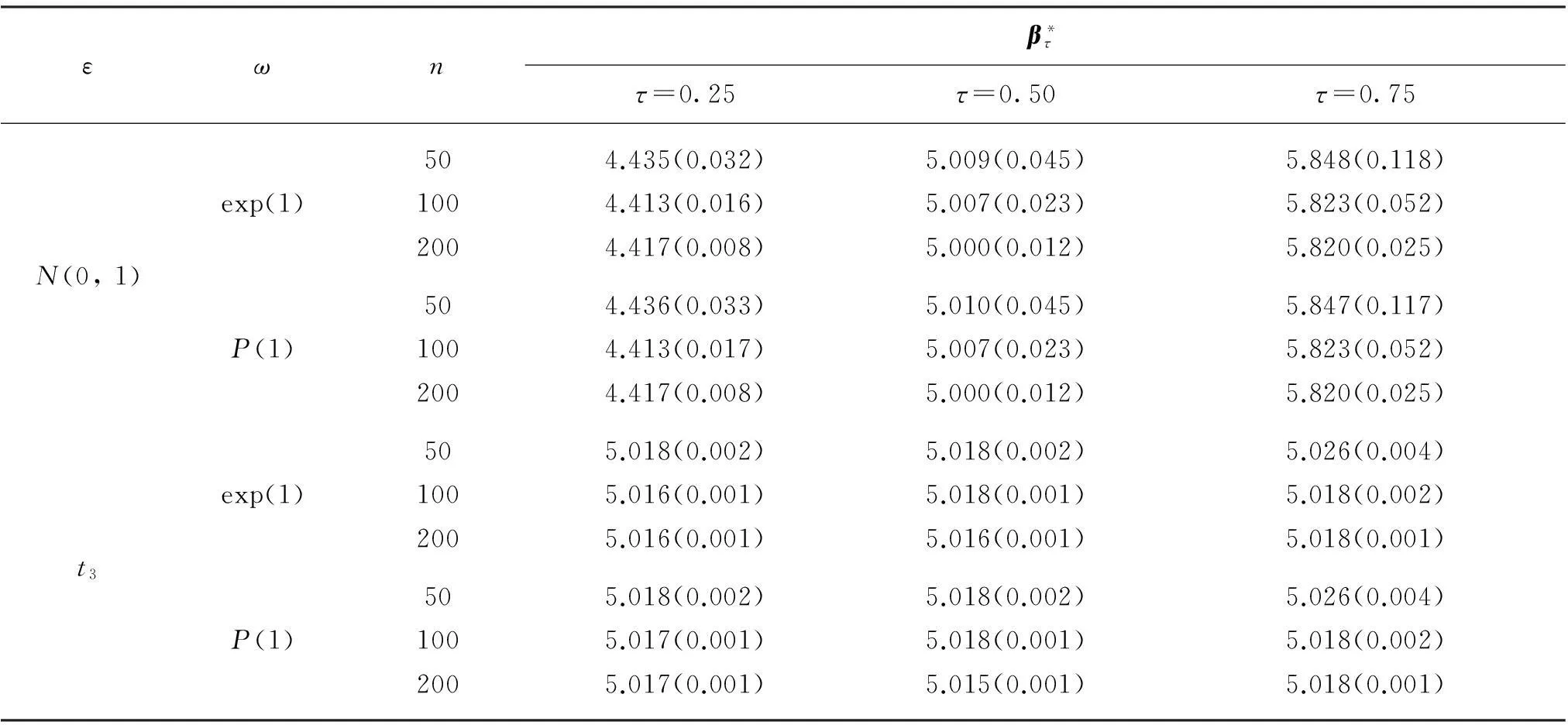
εωnβ*ττ=0.25τ=0.50τ=0.75N(0,1)504.435(0.032)5.009(0.045)5.848(0.118)exp(1)1004.413(0.016)5.007(0.023)5.823(0.052)2004.417(0.008)5.000(0.012)5.820(0.025)504.436(0.033)5.010(0.045)5.847(0.117)P(1)1004.413(0.017)5.007(0.023)5.823(0.052)2004.417(0.008)5.000(0.012)5.820(0.025)t3505.018(0.002)5.018(0.002)5.026(0.004)exp(1)1005.016(0.001)5.018(0.001)5.018(0.002)2005.016(0.001)5.016(0.001)5.018(0.001)505.018(0.002)5.018(0.002)5.026(0.004)P(1)1005.017(0.001)5.018(0.001)5.018(0.002)2005.017(0.001)5.015(0.001)5.018(0.001)

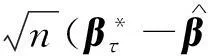
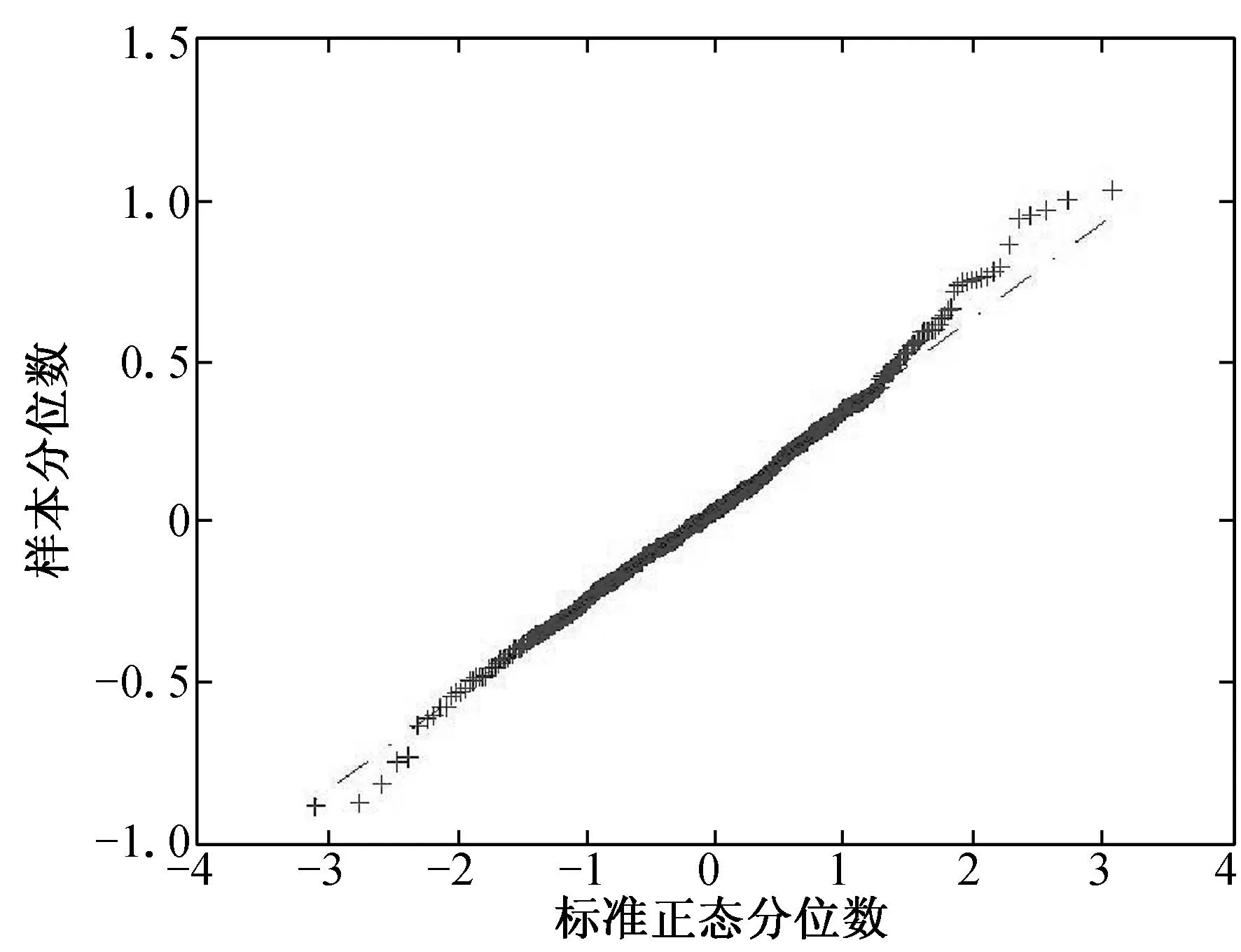
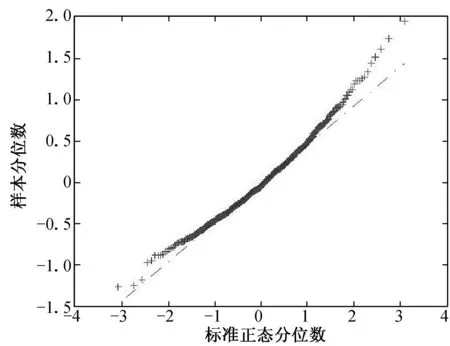
(a) n=100， τ=0.25　(b) n=100， τ=0.50　(c) n=100， τ=0.75

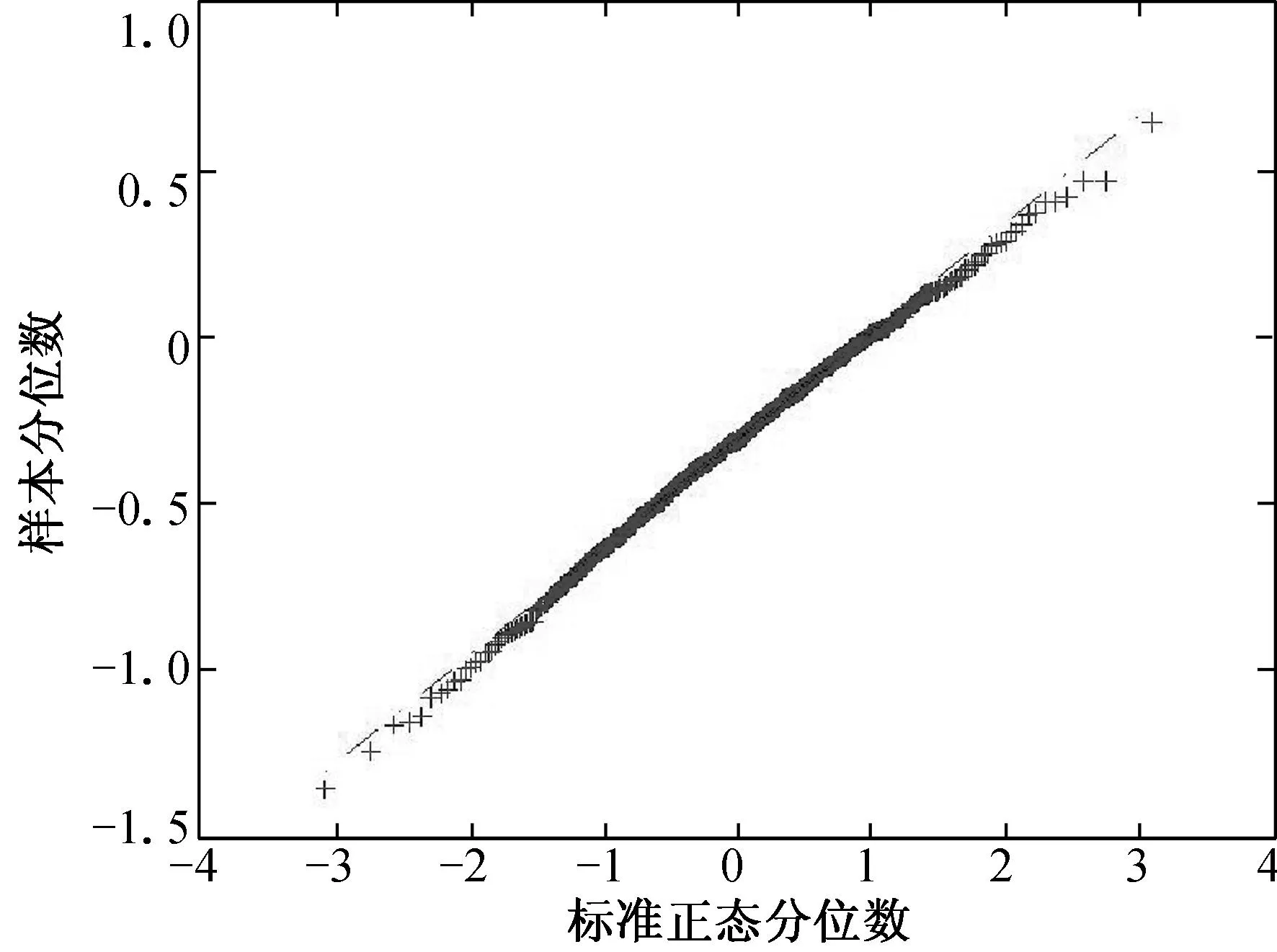
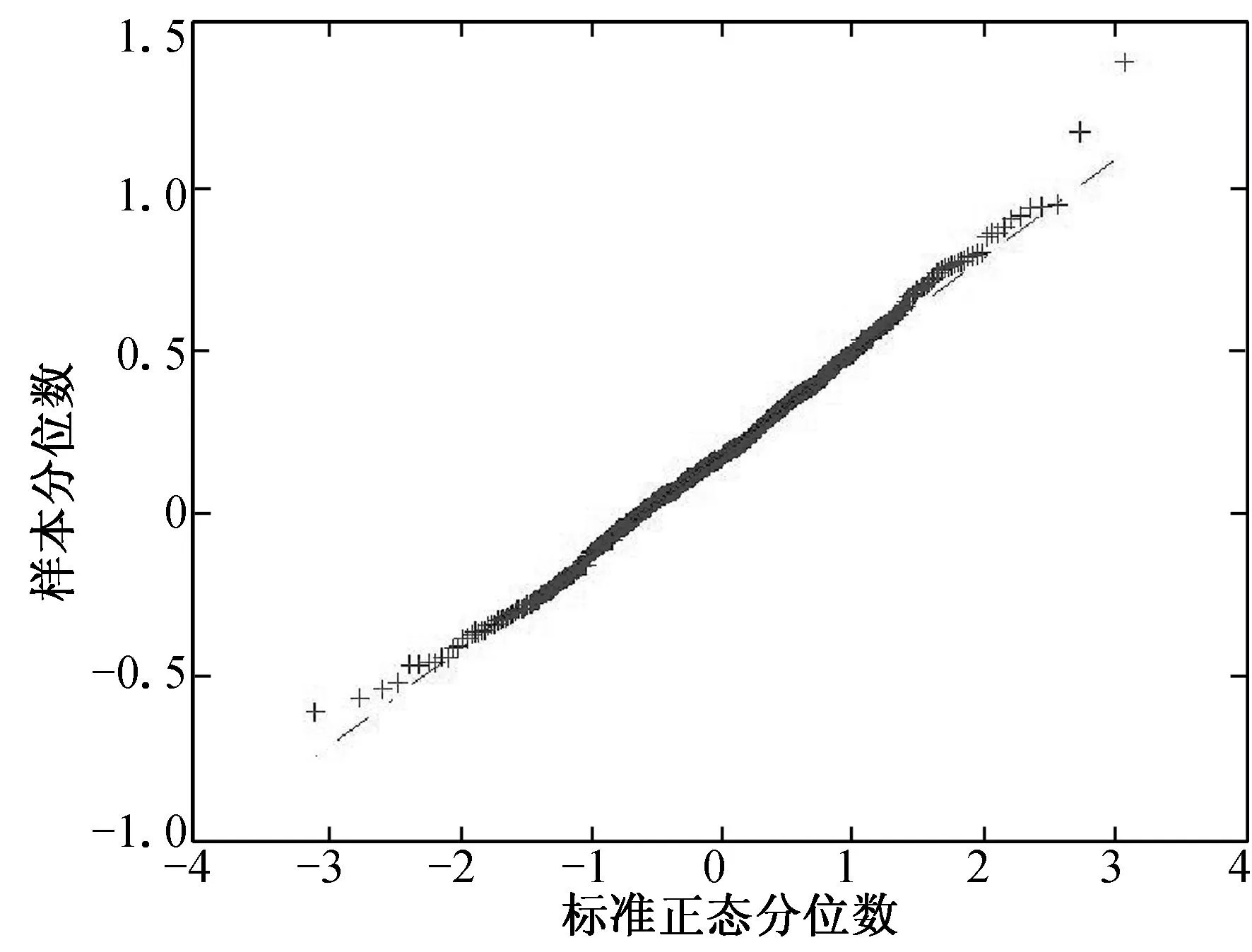
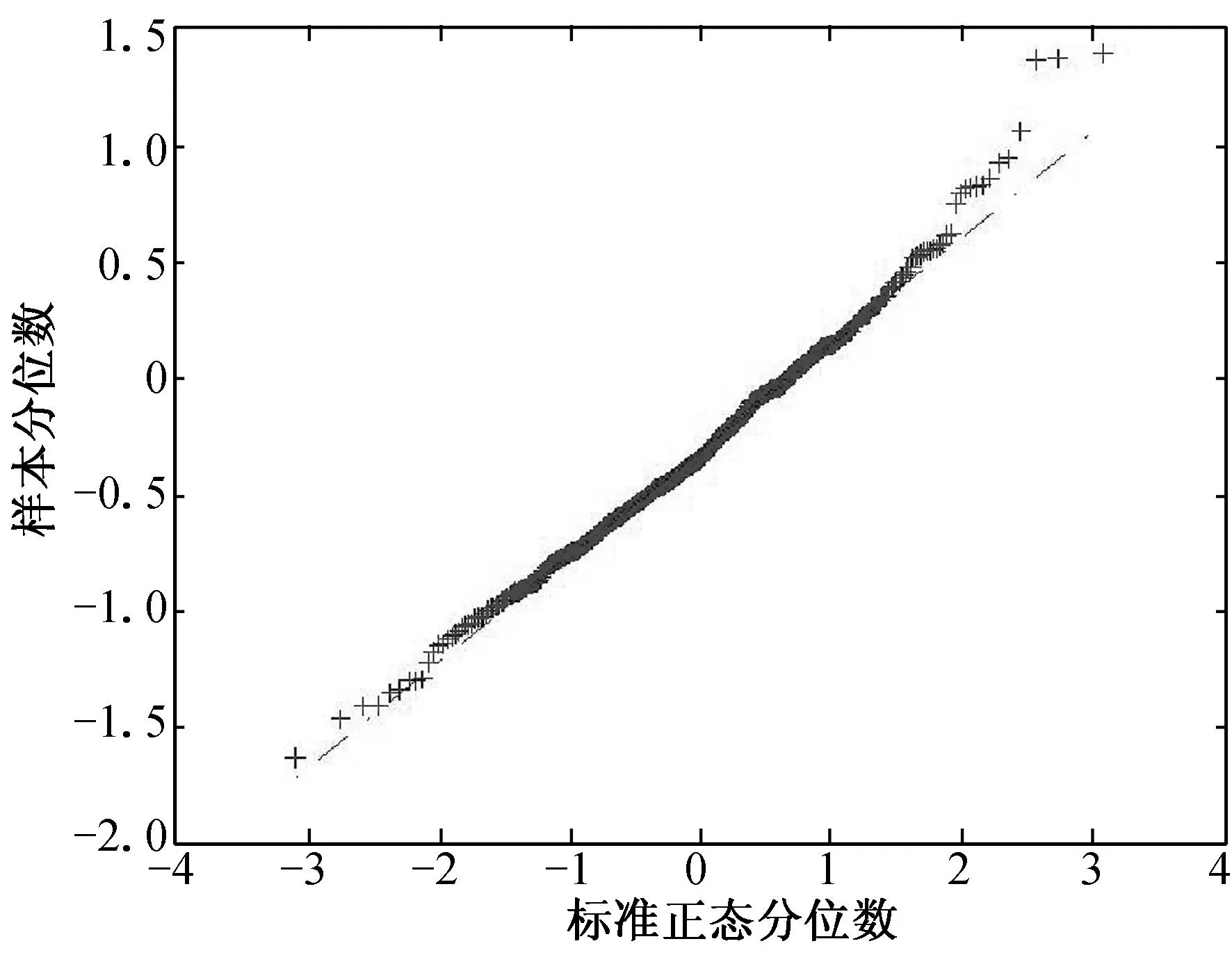
(d) n=200， τ=0.25　(e) n=200， τ=0.50　(f) n=200， τ=0.75

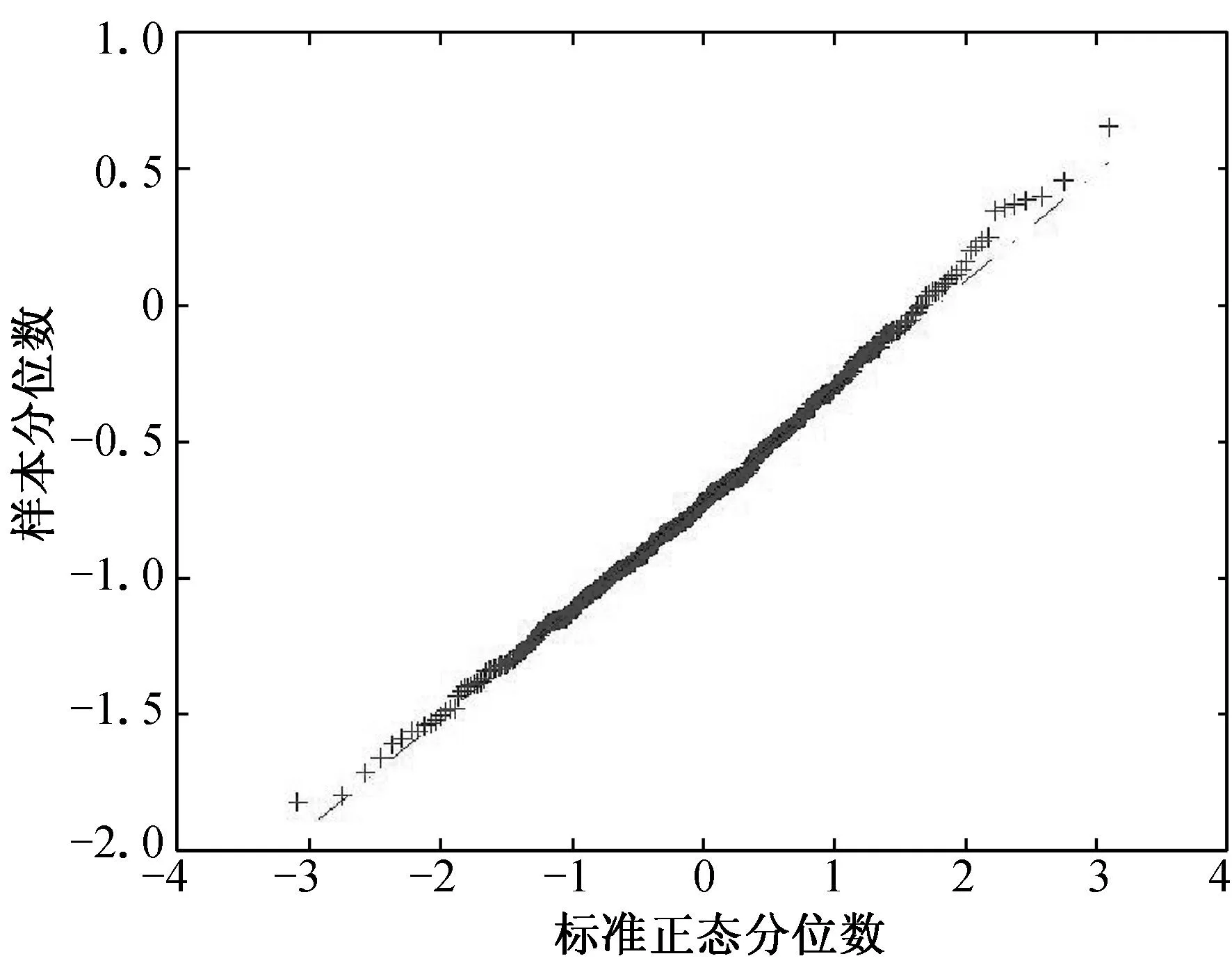
(a) n=100， τ=0.25　(b) n=100， τ=0.50　(c) n=100， τ=0.75

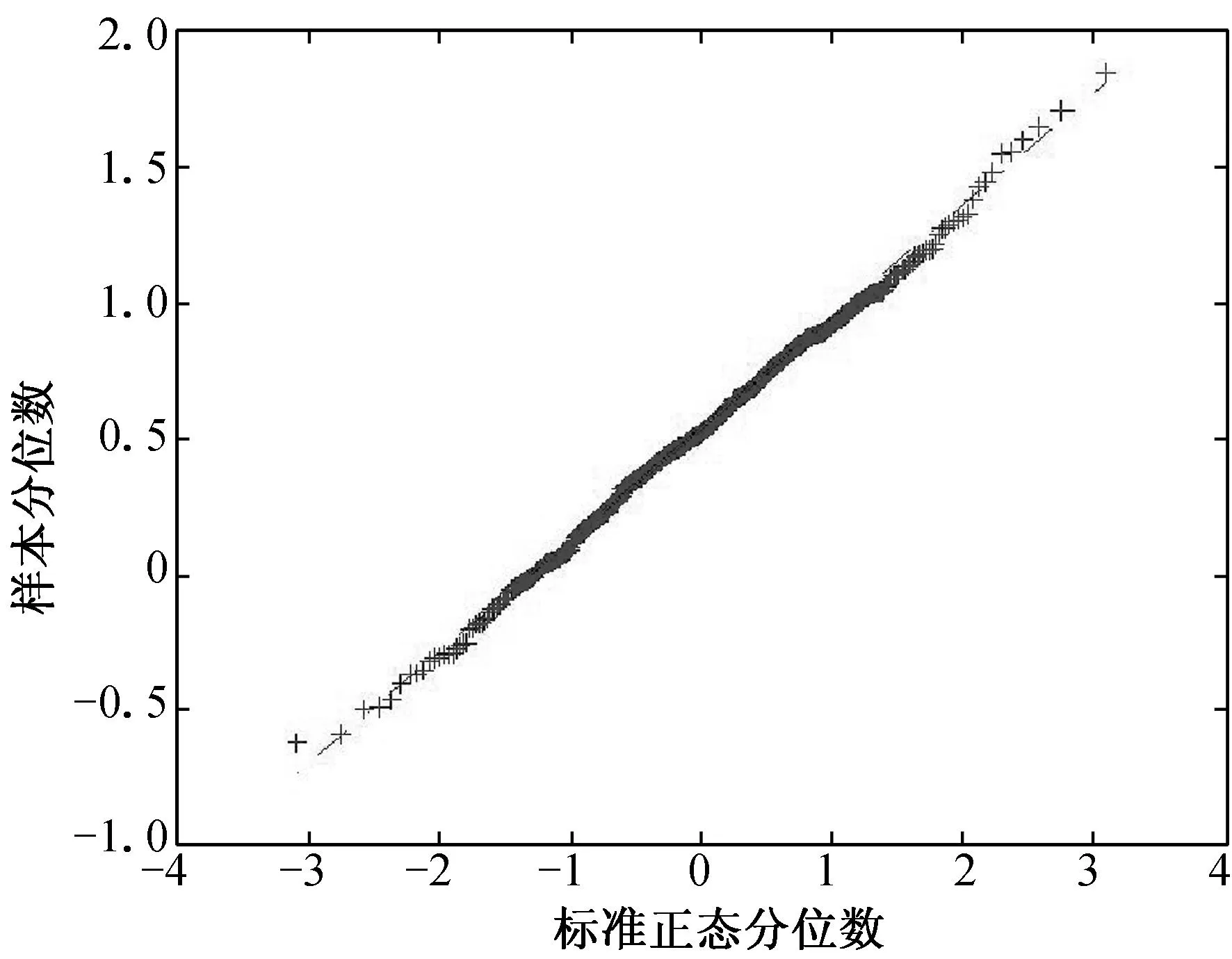
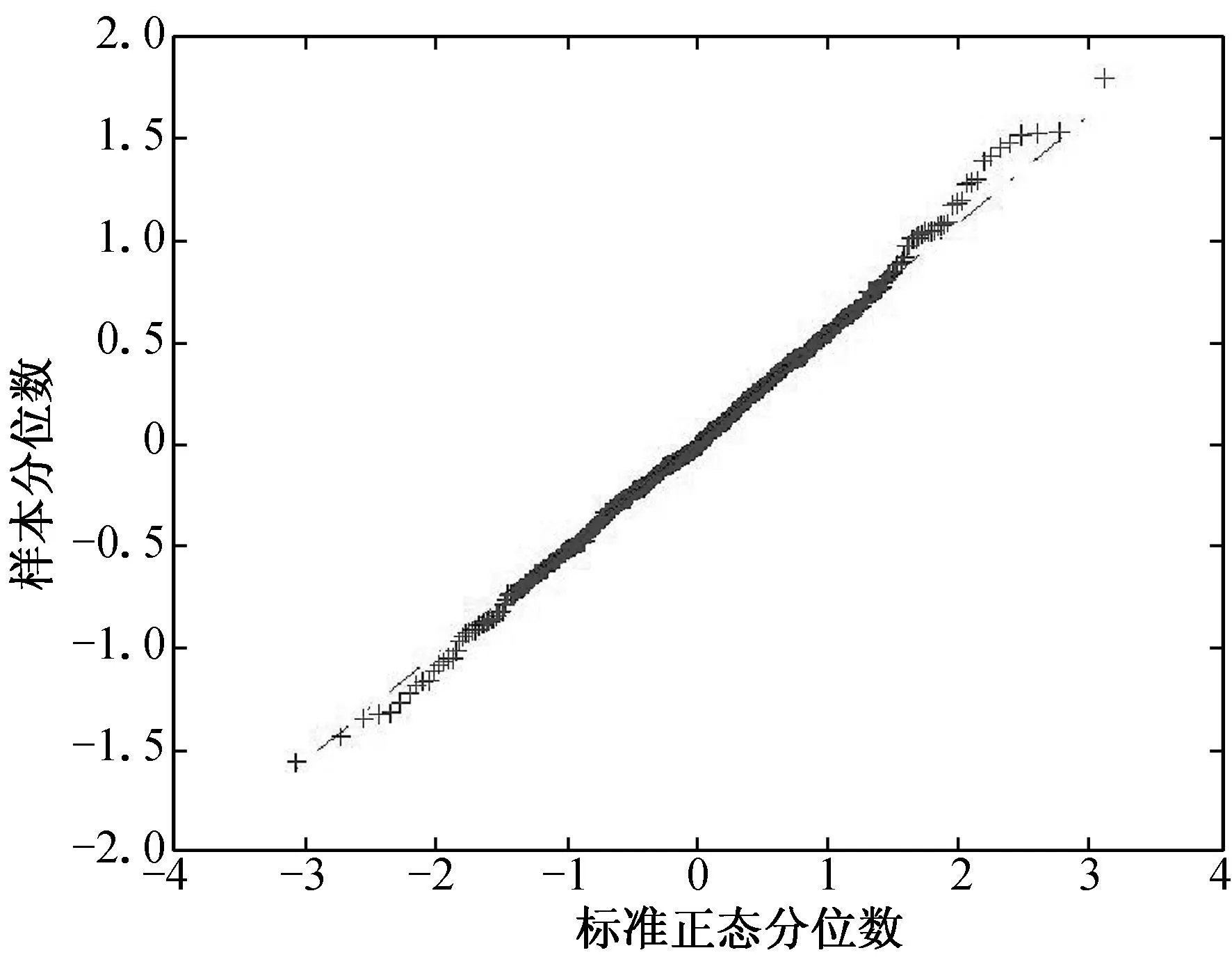
(d) n=200， τ=0.25　(e) n=200， τ=0.50　(f) n=200， τ=0.75

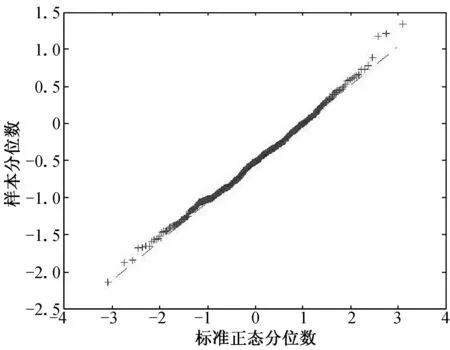
(a) n=100， τ=0.25　(b) n=100， τ=0.50　(c) n=100， τ=0.75

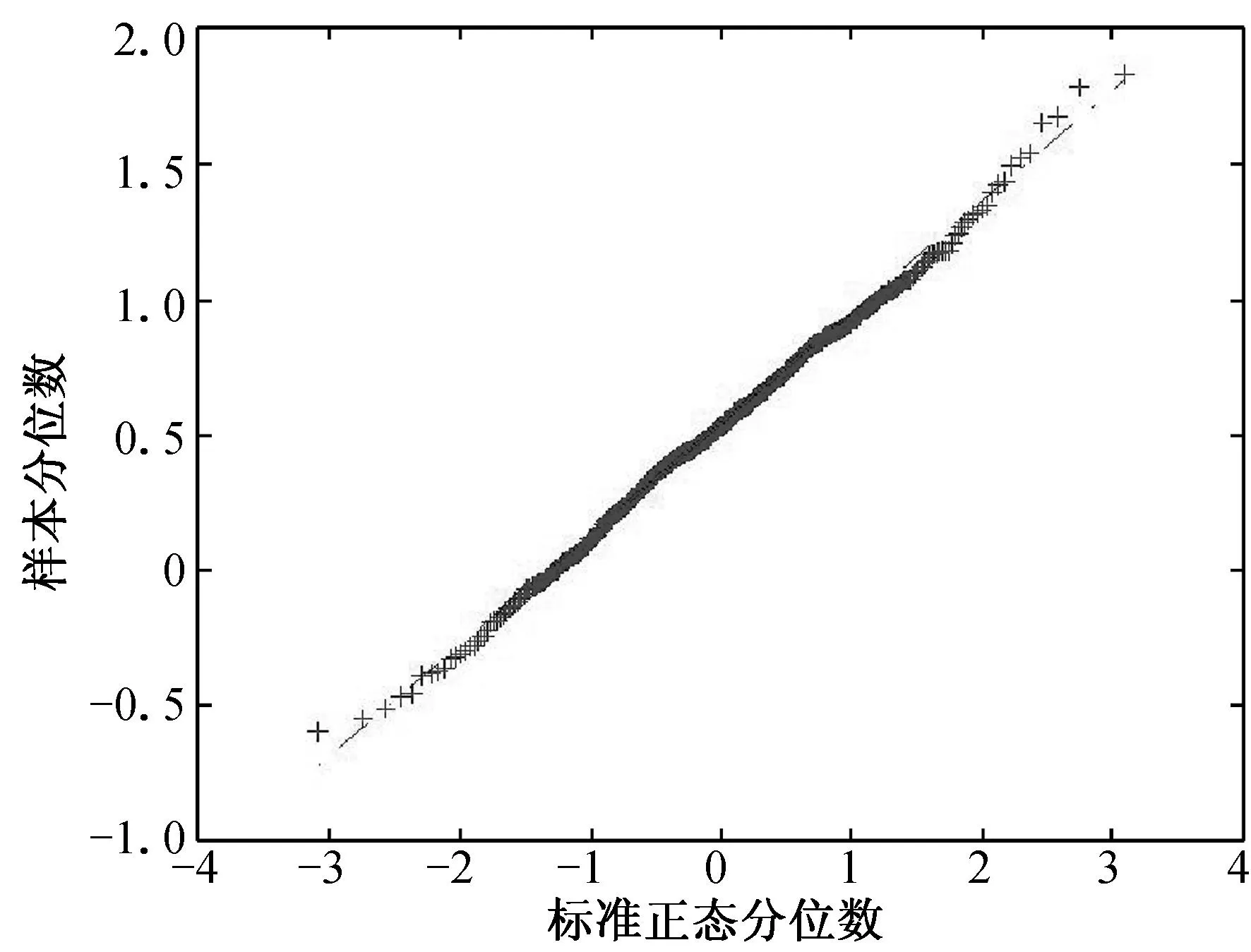
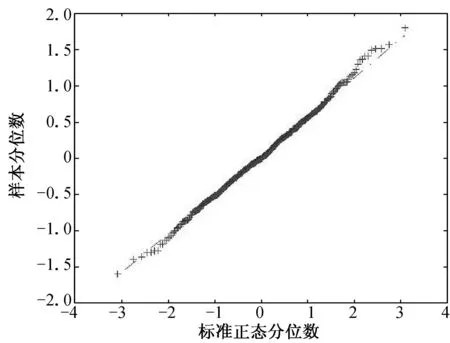
(d) n=200， τ=0.25　(e) n=200， τ=0.50　(f) n=200， τ=0.75

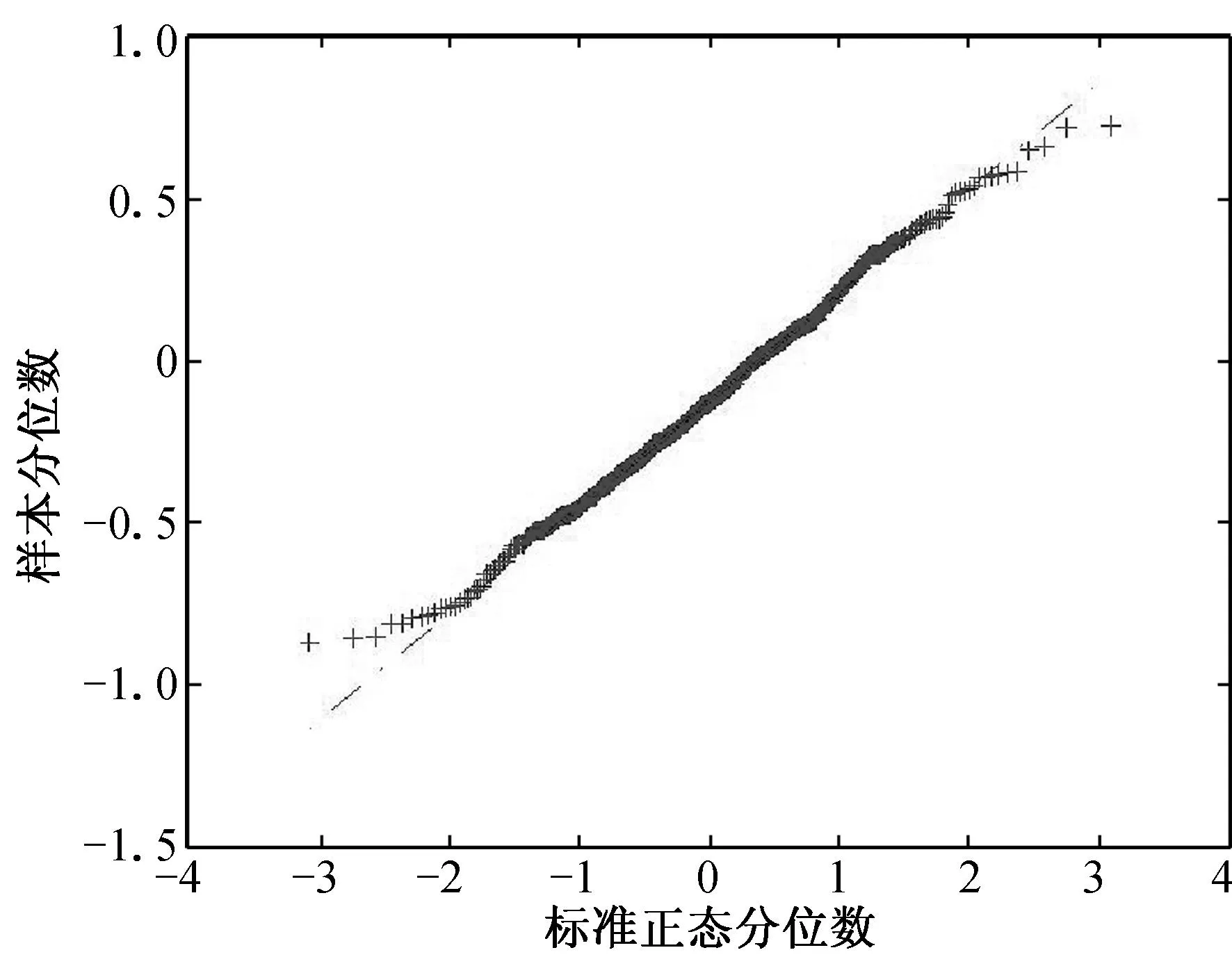
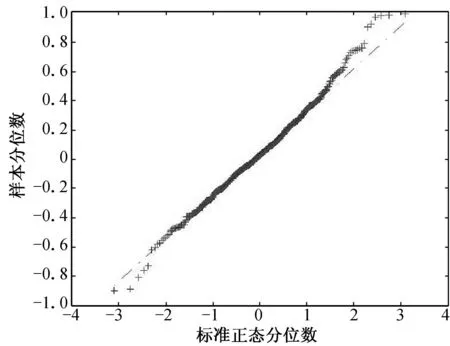
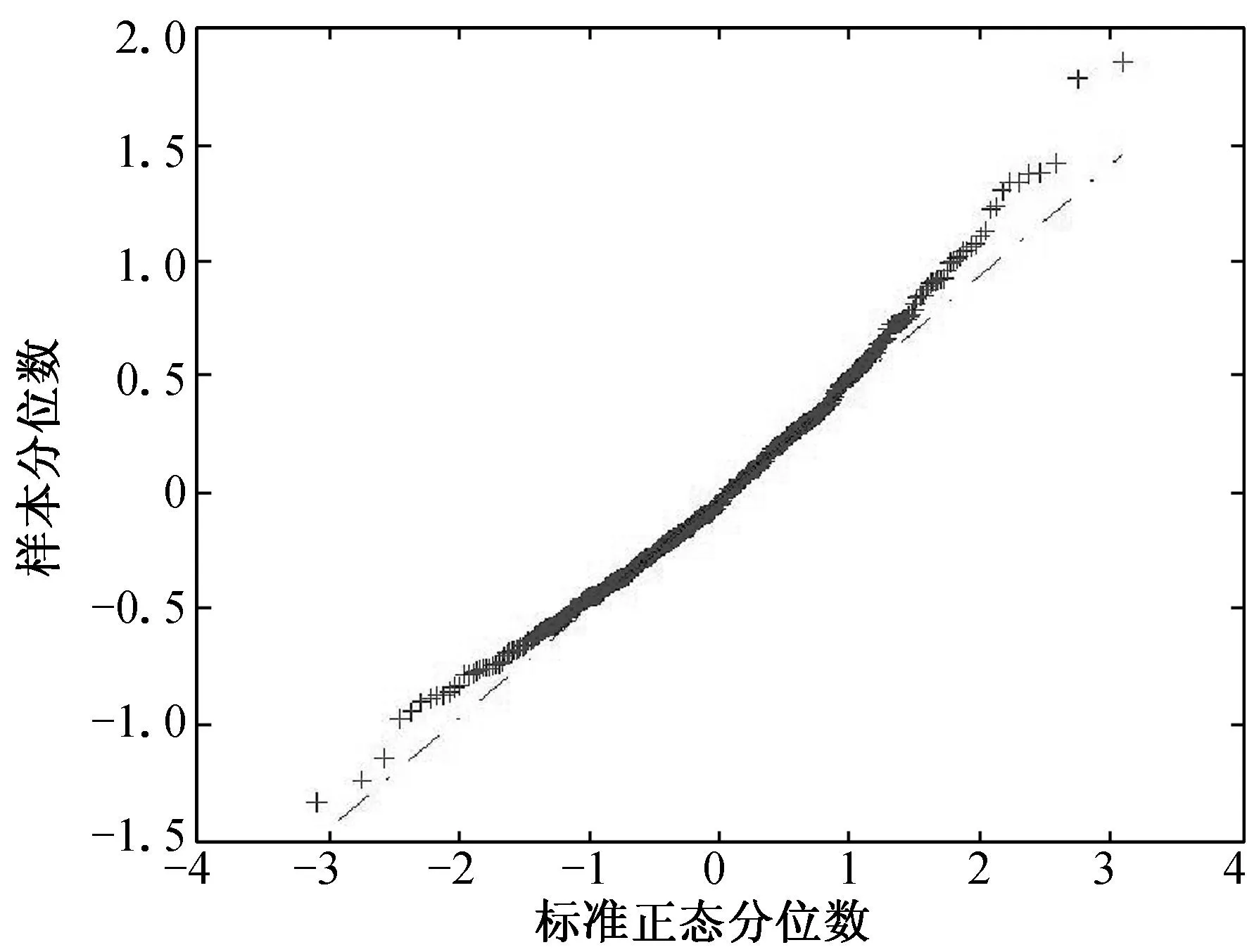
(a) n=100， τ=0.25　(b) n=100， τ=0.50　(c) n=100， τ=0.75

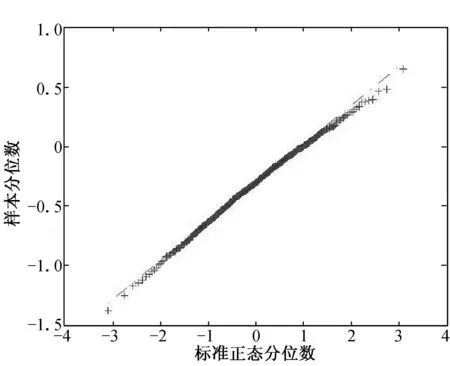
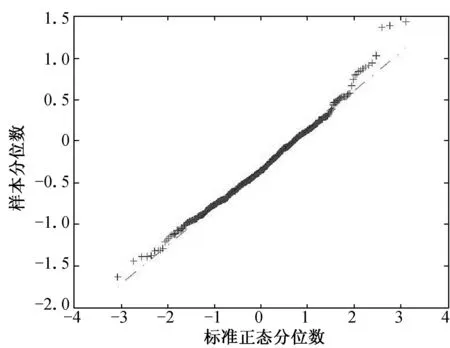
(d) n=200， τ=0.25　(e) n=200， τ=0.50　(f) n=200， τ=0.75

例2对艾滋病临床试验组(ACTG315)的研究数据进行分析.一般情况下，认为病毒学反应的RNA(由病毒载量反映)和免疫反应(由CD4+细胞计数反映)在治疗过程中呈负相关.本研究的目的之一是调查艾滋病的临床试验中病毒学反应的RNA和免疫反应之间的关系.初步调查表明，病毒载量线性依赖于CD4+细胞计数.因此，根据模型(1)建立病毒载量及CD4+细胞计数之间的关系模型为

式中：x为存在测量误差的随机变量[19]，这里x为实际的CD4+细胞计数；Y为病毒载量；X为观测到的CD4+细胞计数.

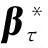
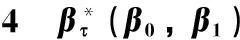
ωβ*ττ=0.25τ=0.50τ=0.75exp(1)β022.37430.92336.579β1-8.275-11.369-13.230P(1)β022.59630.89636.715β1-8.275-11.369-13.230

从表4看出，当随机加权变量分别取均值为1的指数分布exp(1)和均值为1的泊松分布P(1)时，病毒学反应的RNA和免疫反应在治疗过程中都呈负相关，与预想一致.

3定理证明

3.1定理1的证明

设V是一个对称正定矩阵，U是一个随机变量，An(s)是对角线最小值为αn的凸函数.由文献[20]知，若

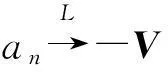
ρτ(x-y)-ρτ(x)=

记

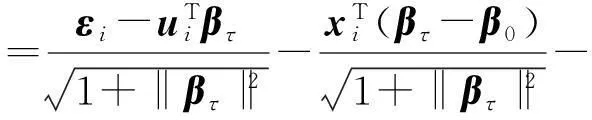
(βτ-β0)+o(1)，

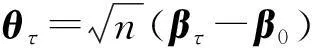
Qn=Qn1+Qn2，

其中

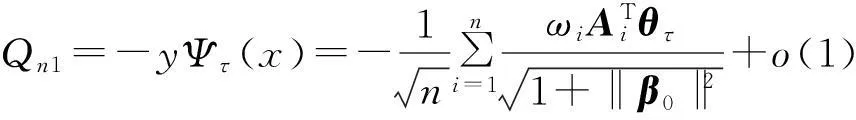
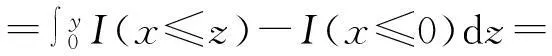
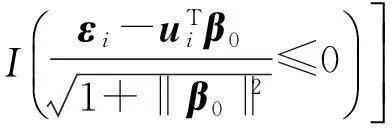
由于

其中∶=d表示服从相同分布.有

因此，

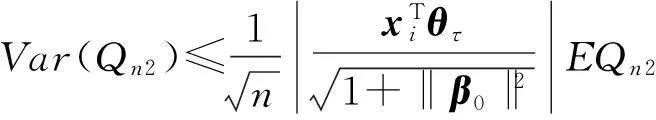
根据条件A2可知，

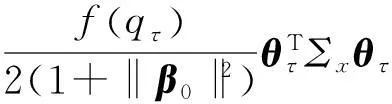
目标函数Q0(θτ)的凸性，确保了极小值的唯一性，可知

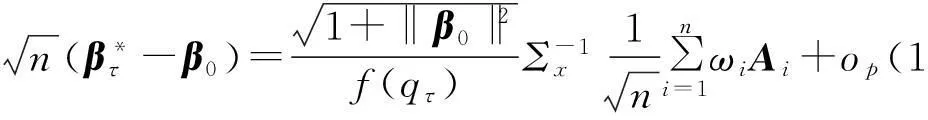
ωi=1，则为

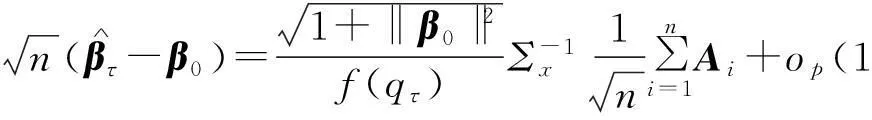
3.2定理2的证明

由定理1可知，

op(1)，

(9)

(10)

由式(9)和(10)可知，

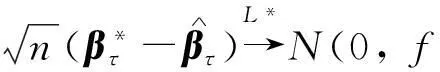
通过运用文献[13]中相似论证，可知式(8)正确.定理证毕.

4结语

本文研究了线性测量误差模型的估计问题，结合分位数回归方法和随机加权法，提出了随机加权分位数回归估计方法.证明了在一定条件下，可以用随机加权法得到分位数回归估计量的渐近分布，这种方法得到的近似分布有许多优点，它避免了估计冗余参数，且实施方便.通过模拟研究验证了所提出的方法的有效性，再用实例研究说明了随机加权分位数回归估计方法具有实际的应用价值.本文提出的方法可以拓展到更多的情形.

参考文献

[1] DEATON A. Panel data from a time series of cross-sections[J]. Journal of Econometrics， 1985， 30(1/2)： 109-126.

[2] FULLER W A. Measurement error models[M]. New York： Wiley， 1987.

[3] HENDRICKS W， KOENKER R. Hierarchical spline models for conditional quantiles and the demand for electricity[J]. Journal of the American Statistical Association， 1992， 87(417)： 58-68.

[4] KOENKER R， HALLOCK K. Quantile regression[J]. Journal of Economic Perspectives， 2001， 15(4)： 143-156.

[5] YANG S. Censored median regression using weighted empirical survival and hazard functions[J]. Journal of the American Statistical Association， 1999， 94(445)： 137-145.

[6] KOENKER R， GELING R. Reappraising medfly longevity： A quantile regression survival analysis[J]. Journal of the American Statistical Association， 2001， 96(454)： 458-468.

[7] WEI Y， HE X M. Conditional growth charts(with discussions)[J]. The Annals of Statistics， 2006， 34(5)： 2069-2097.

[8] KOENKER R. Quantile regression[M]. Cambridge： Cambridge University Press， 2005.

[9] CAI Z， XU X. Nonparametric quantile estimations for dynamic smooth coefficient models[J]. Journal of the American Statistical Association， 2008， 103(484)： 1596-1608.

[10] WANG J L， XUE L G， ZHU L X， et al. Estimation for a partial-linear single-index model[J]. The Annals of Statistics， 2010， 38(1)： 246-274.

[11] KAI B， LI R， ZOU H. New efficient estimation and variable selection methods for semiparametric varying-coefficient partially linear models[J]. The Annals of Statistics， 2011，

39(1)： 305-332.

[12] HE X M， LIANG H. Quantile regression estimates for a class of linear and partially linear errors-in-variables models[J]. Statistica Sinica， 2000， 10(1)： 129-140.

[13] ZHENG Z G. Random weighting method[J]. Acta Mathematicae Applilcate Sinica， 1987， 10(2)： 247-253.

[14] RUBIN D B. The Bayesian bootstrap[J]. The Annals of Statistics， 1981， 9(1)： 130-134.

[15] RAO C R， ZHAO L C. Approximation to the distribution of M-estimates in linear models by randomly weighted bootstrap[J]. Sankhy ā A， 1992， 54(3)： 323-331.

[16] CUI W Q， LI K， YANG Y N， et al. Random weighting method for Cox’s proportional hazards model[J]. Science in China Series A， 2008， 51(10)： 1843-1854.

[17] WANG Z F， WU Y H， ZHAO L C. Approximation by randomly weighting method in censored regression model[J]. Science in China Series A， 2009， 52(3)： 561-576.

[18] 姜荣，钱伟民，周占功. 半参数测量误差模型中参数的随机加权估计[J].同济大学学报(自然科学报)， 2011， 39(5)： 768-772.

[19] LIANG H， WU H L， CARROLL R J. The relationship between virologic and immunologic responses in AIDS clinical research using mixed-effect varying-coefficient semiparametric models with measurement error[J]. Biostatistics， 2003， 4(2)： 297-312.

[20] SHERWOOD B， WAN L， ZHOU X H. Weighted quantile regression for analyzing health care cost data with missing covariates[DB/OL].(2013-09-09)[2014-07-20]. http：//onlinelibrary. wiley.com/d oi/10.1002/sim.5883.

[21] KNIGHT K. Limiting distributions forL1regression estimators under general conditions[J]. The Annals of Statistics， 1998， 26(2)： 755-770.

[22] VAN DER VAART A W， WELLNER J A. Weak convergence and empirical processes[M]. New York： Springer-Verlag， 1996.

Random Weighting Quantile Regression for Linear Errors-in-Variables Models

LIUYing，GEYou-mei，JIANGRong

(College of Science， Donghua University， Shanghai 201620， China)

Abstract：The purpose is to extend the random weighting method to linear errors-in-variables models. By combining the quantile regression， random weighting quantile regression is proposed for linear errors-in-variables models. It is shown that the random weighting quantile regression estimation is uniformly consistent. The random weighting method provides a way of assessing the distribution of the quantile regression estimators without estimating the nuisance parameters. The simulation studies and an AIDS real data application are conducted to illustrate the finite sample performance of the proposed methods.

Key words：errors-in-variables； quantile regression； random weighting method

中图分类号：O 213.9

文献标志码：A

作者简介：刘莹(1991—)，女，浙江衢州人，硕士研究生，研究方向为概率论与数理统计.E-mail： mygirl-ly@163.com

收稿日期：2014-12-05

文章编号：1671-0444(2016)01-0152-08