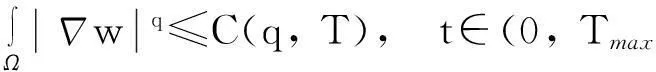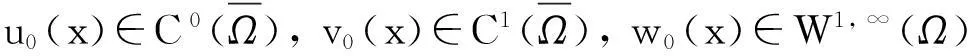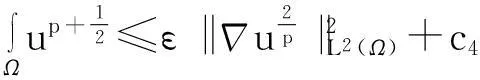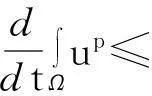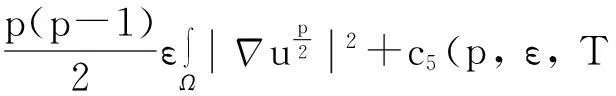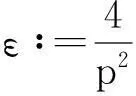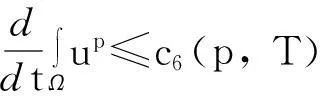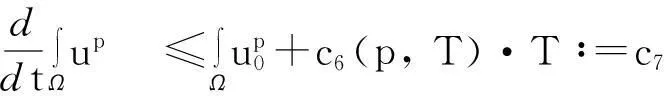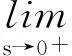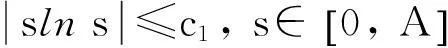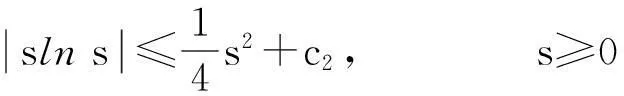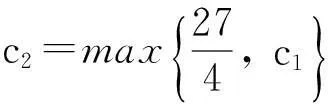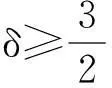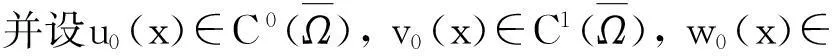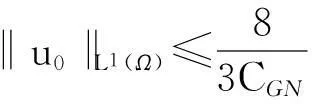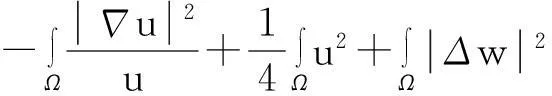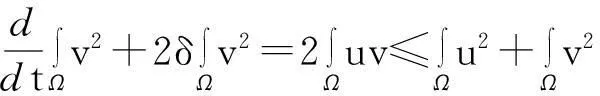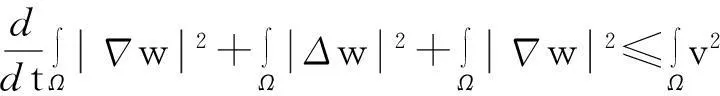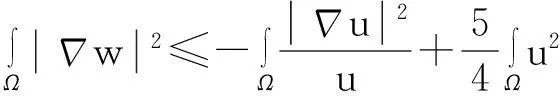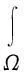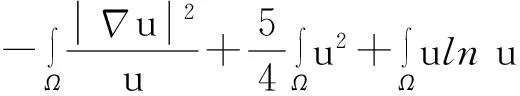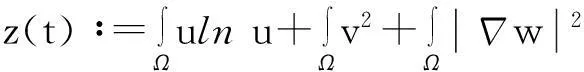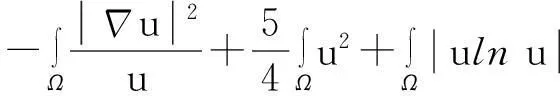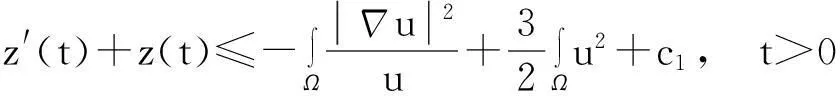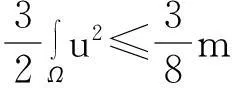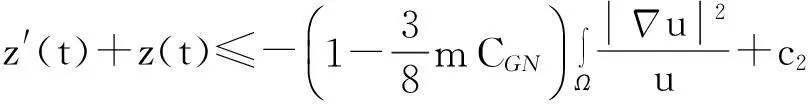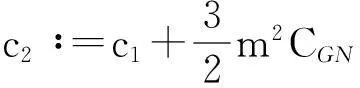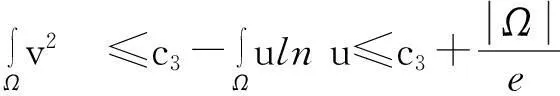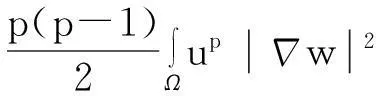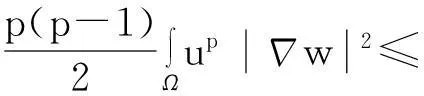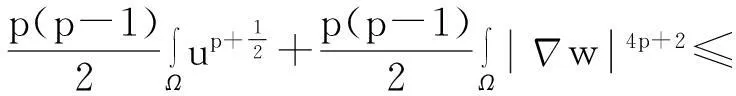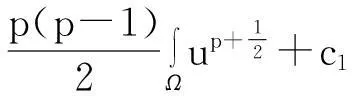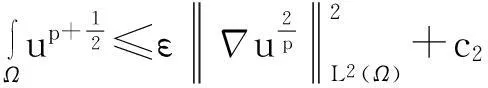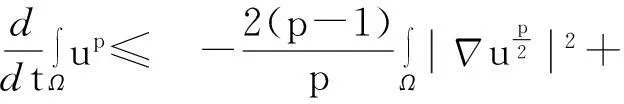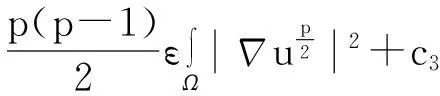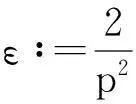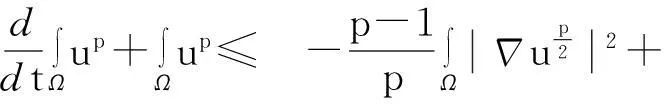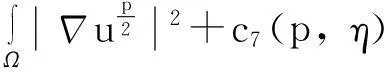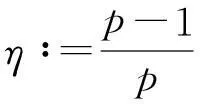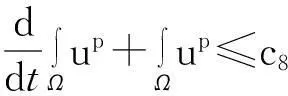二维空间中具间接信号产出趋化模型解的整体存在性
2016-04-20刘冬梅
刘冬梅
(东华大学 信息科学与技术学院, 上海 201620)
二维空间中具间接信号产出趋化模型解的整体存在性
刘冬梅
(东华大学 信息科学与技术学院, 上海 201620)
摘要:考虑一个山松甲壳虫的扩散和聚集趋化模型,该模型由两个反应-扩散方程和一个常微分方程构成.证明了对任意的充分光滑的初始值该模型整体解的存在性,从而排除了解在有限时间爆破的可能性,讨论了该模型在初始细胞质量适当小的假设下整体解的有界性.
关键词:趋化性; 间接信号产出; 整体存在性; 有界性
趋化性是指由信号浓度的空间变化而引起的细胞的偏向运动.著名的趋化数学模型(以下简称KS模型)是由Keller-Segel提出[1].设细胞的密度为u=u(x,t),而相应的信号浓度为w=w(x,t),则上述提及KS模型如下:
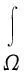
在KS模型的基础上,本文研究的是在文献[8]中提出的关于山松甲壳虫聚集模式的模型.近年来,由于气候变暖,主要生活在加拿大的山松甲壳虫快速繁殖,并给森林造成了巨大的危害.它们把卵产在松树上,直到第二年夏天时,幼虫变为成虫离开树洞,然后继续攻击下一批松树,再准备产卵.需要强调的是:做窝的甲壳虫通过释放一种化学物质来吸引飞行的甲壳虫[8].而本文关心的是这种甲壳虫的扩散和聚集行为.
设飞行的甲壳虫的密度为u=u(x,t),做窝的甲壳虫的密度为v=v(x,t),相应的信号浓度为w=w(x,t),则关于甲壳虫的模型[8]如下:
(1)
其中:Ω⊂Rn是一个光滑有界区域;参数δ>0.模型(1)中,第一个方程描述飞行的甲壳虫密度随时间的变化情况,等式右边第一项表示飞行的甲壳虫的随机扩散,第二项表示飞行的甲壳虫趋向于化学物质浓度增加的方向移动;第二个方程描述做窝的甲壳虫密度随时间变化情况,δ表示相应的死亡率;第三个方程表明化学信号由做窝的甲壳虫产出,并随时间衰减.
模型(1)给出了一个间接信号产出过程,即这种化学物质并不是由飞行的甲壳虫直接产出,而是由飞行甲壳虫转变而来的做窝的甲壳虫产出的.从数学的角度来说,模型(1)和KS模型的一个本质区别在于:由直接信号产出的KS模型,在二维空间中,当初始细胞的质量大于某个特定值时,模型的解会在有限时间爆破;而间接信号产出的模型(1)是不可能在有限时间爆破的.更精确地说:
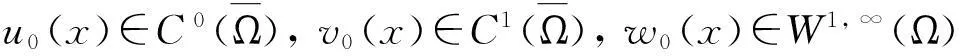
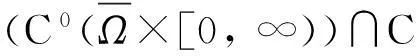
而当t→+∞时,解是否会爆破这一问题,目前尚不清楚,有待进一步深入研究.
如前面所述,KS模型存在临界质量现象.另外一个有趣的问题是模型(1)是否也存在类似的临界质量现象?本文将探讨这一问题.
为了陈述结论,首先回顾Gagliardo-Nirenberg不等式:设Ω⊂R2是一个光滑有界区域,则对任意的u(x)∈W1, 2(Ω),存在CG N=CG N(Ω)>0,使得
成立.
下面陈述有关模型(1)的一个小初值整体解有界的结果.
定理2假设n=2且设
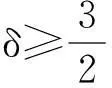
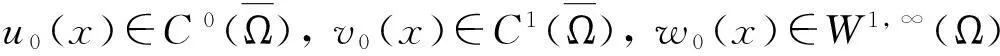
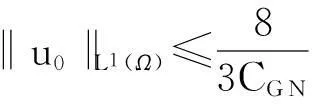
‖u(·, t)‖L∞(Ω)≤C
成立.
1解的整体存在性:定理1的证明
利用合适的不动点方法可以证明关于模型(1)的解的局部存在唯一性结论.
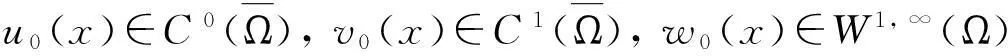
进一步,如果Tmax<∞,则当t→Tmax时,有
‖u(·,t)‖L∞(Ω)→∞.
证明:该证明过程类似于文献[9],故在此不重复其细节.
由引理1.1知,要证明模型(1)的解在Ω×(0, ∞)上存在,需要建立u(·,t)在L∞(Ω)空间中的估计,即要证明:对任何T∈(0,Tmax),存在某个常数C(T),使得
‖u(·, t)‖L∞(Ω)≤C(T),∀t∈(0, T)
(2)
成立.
以下的质量估计是建立估计式(2)的起点.
引理1.2模型(1)的古典解(u,v,w)具有如下性质:
‖u(·, t)‖L1(Ω)=‖u0‖L1(Ω),t∈(0, Tmax),
(3)
‖v(·, t)‖L1(Ω)≤
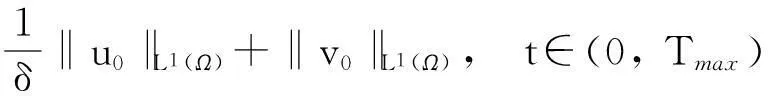
(4)
‖v0‖L1(Ω)+‖w0‖L1(Ω),t∈(0, Tmax).
(5)
证明:模型(1)中第一个方程在Ω上求积分,并利用分部积分和模型(1)中零流边界条件得
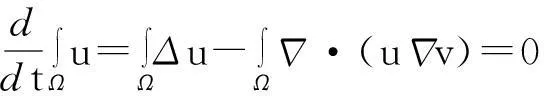
由此推得
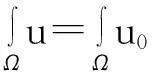
(6)
即式(3)成立.
模型(1)的第二个方程的两边在Ω上求积分得
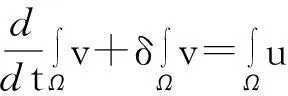
据此并利用式(6)得
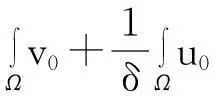
(7)
即式(4)成立.
类似地,有
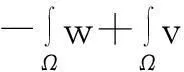
解之并根据式(7)得
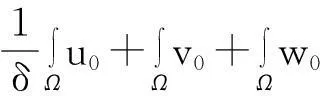
从而式(5)得证.

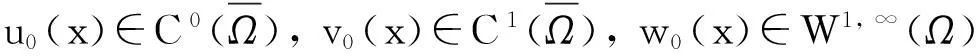
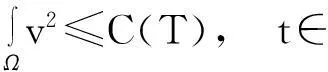
证明:模型(1)中第一个方程两边同时乘以lnu后再在Ω上积分,并利用分部积分、零流边界条件及Young不等式得

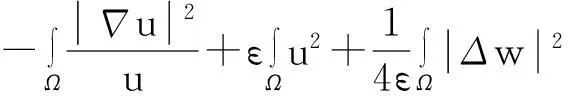
(8)
其中:ε>0为任意常数.
接下来,模型(1)中第二个方程两边同时乘以2v后在Ω上积分,并利用Young不等式得
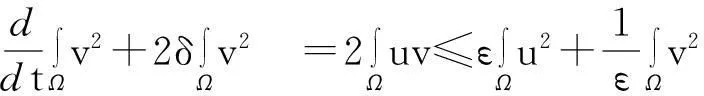
(9)
再由模型(1)中第三个方程两边同时乘以(-Δw)后在Ω上积分得
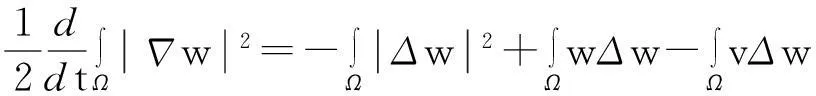
由此并利用Young不等式得
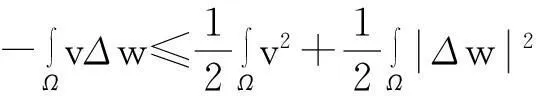
从而
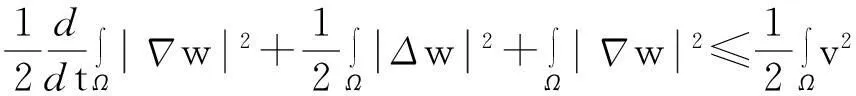
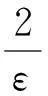
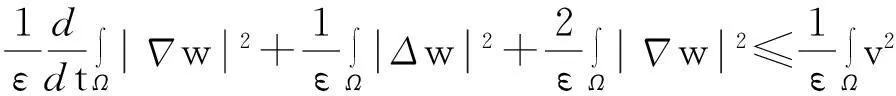
(10)
综合式(8)~(10)得
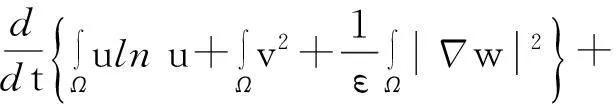
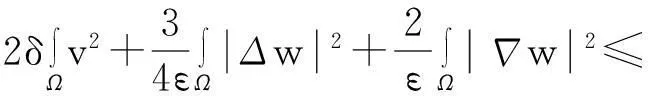
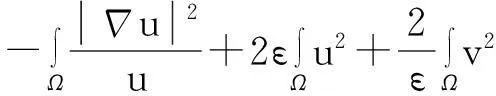
(11)
利用Gagliardo-Nirenberg不等式进一步估计式(11)中右边第二个积分
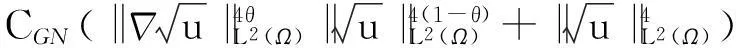
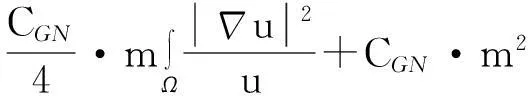
(12)
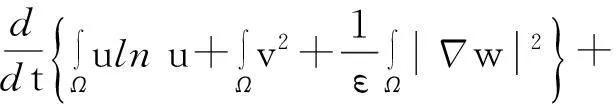
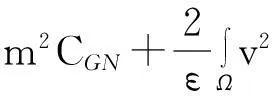
舍弃不等式左边后3个非负项得
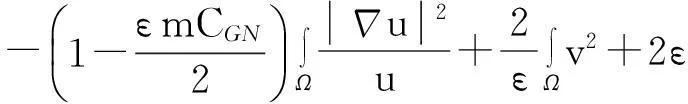
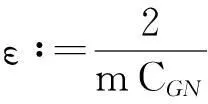
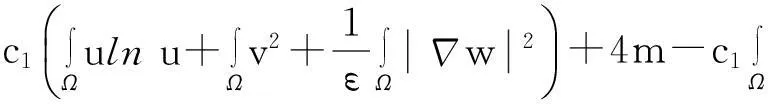
(13)
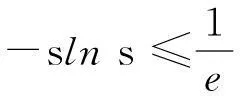
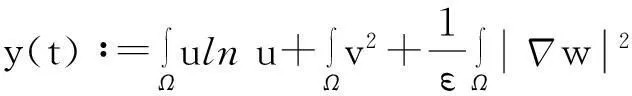
则式(13)变为
y′(t)≤c1y(t)+c2,
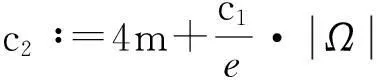
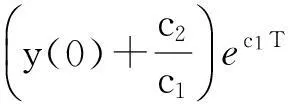
即
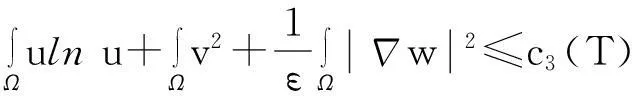
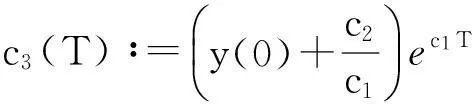
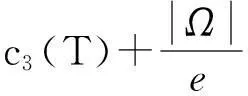
从而引理1.3得证.
为了建立u的Lp估计,需先引入下列关于热方程的正则性引理[9].
引理1.4假设n=2并设z0∈W1, ∞(Ω), f∈L2(Ω),z满足方程
则对任意的1 ‖z‖W1, q(Ω)≤C(q)‖f‖L2(Ω),t>0. (14) 证明:根据模型(1)中第三个方程知,式(14)是引理1.3和1.4的直接推论. (15) 成立. 证明:根据模型(1)中的第一个方程直接计算,并利用Cauchy不等式得 (16) 进一步,由式(14)得:存在某个常数c1(p,T),使得 (17) 再利用Gagliardo-Nirenberg不等式及式(3)估计式(17)中右边的积分 因此 从而由Young不等式得 (18) 综合式(16)~(18)得 因此 引理1.6得证. 定理1的证明:根据模型(1)中的第一个方程,利用估计式(14)和(15)及标准的Moser迭代[10]可以得到 ‖u(·, t)‖L∞(Ω)≤C(T),t∈(0, T). (19) 据此并利用引理1.1及其中的延拓准则知: Tmax=+∞, 从而定理1得证. 2解的有界性:定理2的证明 由解的整体存在性的证明过程可以看出,要证明模型(1)的解在Ω×(0, ∞)上有界,关键要建立u的Lp(Ω)(关于t的)一致先验估计.下面的基本引理在后面将会用到. 引理2.1存在常数C>0,使得 (20) 成立. 证明:利用洛必达法则得 因此,存在某个常数A>1,使得s>A时成立 从而由Young不等式得 (21) 又因为 所以,存在c1>0, 满足 (22) 综合式(21)和(22)得 下面建立v的L2一致先验估计. 引理2.2令n=2. 假设 (23) (24) 则存在某个常数C>0,使得模型(1)的解满足 (25) 证明:由式(8)得 (26) 再由式(9)得 (27) 最后由式(10)得 (28) 综合式(26)~(28)得 由假设式(23)知:2δ-3≥0,因此 t>0, 满足 t>0. 再根据引理2.1知 (29) 由式(12)得 (30) 将式(30)代入式(29)得 t>0, z′(t)+z(t)≤c2. 解之得 z(t)≤z(0)e-t+c2(1-e-t)≤ z(0)+c2∶=c3,t>0. 因此 引理2.2证毕. 根据引理2.2和1.4可以直接得到下面的推论. (31) 成立. 接下来,建立u的Lp(Ω)一致先验估计. (32) 成立. 证明:由式(16)得 (33) 进一步,利用Young不等式及式(31)得:存在某个常数c1(p)满足 (34) 由式(18)得 (35) 综合式(33)~(35)得 (36) 根据Young不等式得:存在常数c5(p)>0,使得 成立,由此并利用式(35)得 (37) 其中:η>0为任意常数.将式(37)代入式(36)的右边得 解之得 因此引理2.4得证. 定理2的证明:根据模型(1)中的第一个方程,利用估计式(31)和(32)及标准的Moser迭代[10]可以得到:存在常数C>0,满足 ‖u(·, t)‖L∞(Ω)≤C,t>0. 由此定理2得证. 参考文献 [1] KELLER E F, SEGEL L A. Initation of slime mold aggregation viewed as an instability[J]. J Theor Biol, 1970, 26(3): 399-415. [2] HORSTMANN D. From 1970 until present: The Keller-Segel model in chemotaxis and its consequences[J]. Jahresber Der Deutsch Math-Verein, 2003, 105(3): 103-165. [3] HILLEN T, PAINTER K. A users’ guide to PDE models for chemotaxis[J]. J Math Biol, 2009, 58(1/2): 183-217. [4] OSAKI K, YAGI A. Finite dimensional attractors for one-dimensional Keller-Segel equations[J]. Funkcial Ekvac, 2001, 44(3): 441-469. [5] NAGAI T, SENBA T, YOSHIDA K. Application of the Trudinger-Moser inequality to aparabolic system of chemotaxis[J]. Funkcial Ekvac Ser Int, 1997, 40(3): 411-433. [6] NAGAI T. Blow up of nonradial solutions to parabolic-elliptic systems modeling chemotaxis in two-dimensional domains[J]. J Inequal Appl, 2001, 6(1): 37-55. [7] WINKLER M. Finite-time blow-up in the higher-dimensional parabolic-parabolic Keller-Segel system[J]. J Math Pures Appl, 2013, 100(5): 748-767. [8] STROHM S, TYSON R C, POWELL J A. Pattern formation in a model for Mountain Pine Beetle dispersal: Linking model predictions to data[J]. Bull Math Biol, 2013, 75(10): 1778-1797. [9] HORSTMANN D, WINKLER M. Boundedness vs. blow-up in a chemotaxis system[J]. J Differential Equations, 2005, 215(1): 52-107. [10] TAO Y S, WINKLER M. Boundedness in a quasilinear parabolic-parabolic Keller-Segel system with subcritical sensitivity[J]. J Differential Equations, 2012, 252(1): 692-715. Global Existence in the Two-Dimensional Chemotaxis Model with Indirect Signal Production LIUDong-mei (College of Information Science and Technology, Donghua University, Shanghai 201620, China) Abstract:A chemotaxis model describing the diffusion and aggregation of the Mountain Pine Beetle is considered. The model consists of two reaction-diffusion equations and an ordinary differential equation. It is shown that the model admits global solution for arbitrarily sufficiently smooth initial data, which excludes the possibility of finite-time blow-up. The boundedness of solutions is asserted whenever the initial cell mass is appropriately small. Key words:chemotaxis; indirect signal production; global existence; boundedness 中图分类号:O 175.26 文献标志码:A 作者简介:刘冬梅(1987—),女,安徽宿州人,博士研究生,研究方向为偏微分方程及应用.E-mail: liudongmei121@sina.cn 收稿日期:2014-12-01 文章编号:1671-0444(2016)01-0137-08