基于随机区间损益市场模型的未定权益无差异定价
2016-04-20尤苏蓉
尤苏蓉,魏 康
(东华大学 理学院,上海 201620)
基于随机区间损益市场模型的未定权益无差异定价
尤苏蓉,魏康
(东华大学 理学院,上海 201620)
摘要:基于加权期望效用最大化,给出了有随机区间损益未定权益的无差异买入价和卖出价的定义,讨论了两种无差异价格的存在性及其性质.通过一个算例,利用二分法得到了简单的二叉树模型下的无差异价格.
关键词:未定权益; 随机区间; 期望效用; 无差异定价
在传统随机金融市场模型中,证券收益表现为随机变量或随机过程.资产定价,特别是未定权益定价,主要有两种方法:一是基于无套利定价方法的风险中性定价;二是基于期望效用优化的效用定价.两种定价方法的主要区别在于风险中性定价由基础市场结构决定,与投资者的消费行为无关,是一种客观定价方法;而效用定价是基于投资者的消费行为特征,以期望效用最大化为基础,可以认为是一种主观定价方法.众所周知,风险中性定价的结论可以表述为“未定权益的无套利价格等于其未来损益在风险中性定价测度下的贴现期望”[1].在效用定价方法中,出现了3种分析方法:一是利用期望效用最大化组合的损益表现,可以构造风险中性定价测度,这也是期望效用优化与风险中性定价方法之间相互联系的表现;二是公平价格概念[2],其基本思想是与仅投资于基本证券给投资者带来的期望效用相比,以公平价格对未定权益进行买卖所产生的边界期望效用为零;三是无差异定价[3-4],未定权益的无差异价格与持有未定权益的单位数多少相关,是一种非线性的定价方法.简单地说,以无差异价格持有相应数量的未定权益并且同时投资于基本证券所产生的最大期望效用与仅投资于基本证券所产生的最大期望效用相等.无差异定价方法被广泛地用于金融分析,如文献[5]讨论了资产在常相对风险厌恶型效用函数情形下的无差异价格,文献[6]讨论了任意效用函数下的未定权益无差异价格及其保值问题.
传统的金融市场模型以及不确定金融市场模型[7],都是以典型的概率空间为基础.两个市场模型的差别在于概率测度是否唯一,在不确定金融市场模型中概率测度不唯一确定,而是在一个概率测度集合中取值.在这两种模型中,相同之处在于资产的表现都是用随机变量或者随机过程描述.近年来,相应于不同形式的不确定原因,其他一些不确定量表示方法,如模糊数、模糊随机变量、区间数以及随机集合被广泛地用于金融分析:用模糊数表示资产收益,构建模糊收益资产的均值-方差组合选择模型[8];基于模糊二叉树的新型期权定价[9];将不确定参数引入经典二叉树模型,在多期时间框架下对期权进行定价分析[10].文献[11]提出了随机区间值收益证券构成的金融市场模型,在这个新模型下,所有证券的收益由随机区间描述.基于可接受市场概念[11],经典单期市场下的定价结论得到了推广.新的市场模型产生一些新的结论,经典的风险中性定价测度被推广为可接受市场价格向量;而未定权益定价的无套利价格区间被推广为可接受价格区间.
关于随机区间市场模型下的期望效用优化问题,依托随机区间的期望以及区间数的评价规则[12],加权期望效用模型[13]被用于衡量投资者对待随机区间收益资产的满意度.在适当的效用函数条件下,市场的可接受性保证了最优交易策略的存在性,并且利用最优投资策略可以产生与经典金融分析中类似的现象[13].在随机区间收益市场下,未定权益的公平价格概念在文献[14]得到了较为详尽的讨论.本文将无差异定价的概念推广到随机区间收益市场中,并讨论新的市场模型下无差异价格的表现及其性质.
1市场模型与加权期望效用
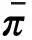
i=1, 2, …, N, j=1, 2, …, M}
(1)
现列出一些与本文内容有关的随机区间损益市场的定价及效用优化概念及已有结论.
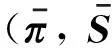
定义2[11]称元素全为正的M值向量ψ≫0,为市场的可接受状态价格向量,若成立
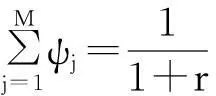
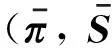
记Ψ为所有的可接受状态价格向量构成的集合.在可接受市场中,一个未定权益可以表示为元素为区间数的M维向量,如式(2)所示.
(2)
(3)
(5)

(6)
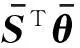
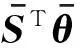
(1+r)e+(S-(1+r)π)Tθ
从而(P1)可以表示为如下仅涉及风险证券投资策略的简化规划:
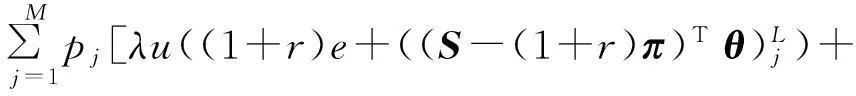
s.t.θ∈RN
区间数的运算规则中一个实数与一个区间数相乘将有比较复杂的情形:设k为实数,[a-, a+]为一个区间数,则k[a-, a+]=[k+a--k-a+, k+a+-k-a-],其中k+=max(k, 0),k-=min(k, 0).在(P1)中,((S-(1+r)π)Tθ)L与((S-(1+r)π)Tθ)U将有复杂的形式.幸运的是,利用效用函数u的凹性,λ∈[0.5, 1], (P1)等价于如下易于计算的规划[13]:
(7)
其中:目标函数为
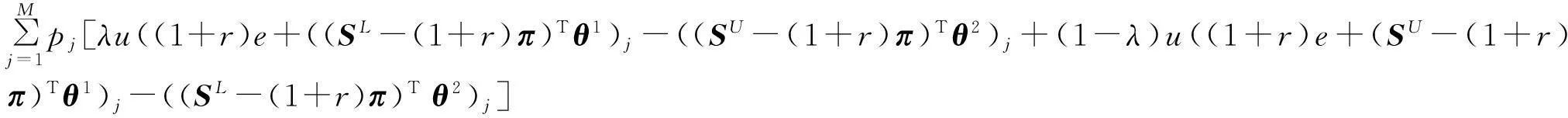
2未定权益的无差异定价及其性质
如同第1节的分析,(P2)可以归结为
(8)
其中:目标函数为
U+(θ1, θ2,b,h)=
显然,规划(P2)的最优值依赖于b和h,记为V+(b, h).
其次,如果投资者以价格h卖空b(b>0)单位X,并使用所获得的收入投资于基本证券,那么对应的规划变为
同样的方法,(P3)等价于
(9)
其中:目标函数为
U-(θ1, θ2,b,h)=
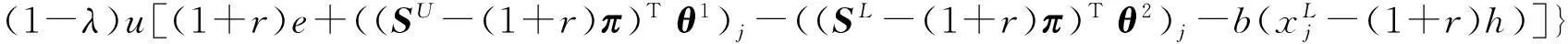
记(P3)的最优值为V-(b, h).
V+(b, h)是投资者以价格h买入b单位X时获得的最优期望效用,而V-(b,h)是投资者以价格h卖空b单位X时获得的最优期望效用.显然,对于任意价格水平h,都有
V+(0, h)=V-(0, h)=W0
(10)
在给出随机区间损益未定权益的无差异价格定义之前,首先给出关于U+(θ1, θ2,b,h),U-(θ1, θ2,b,h)以及V+(b,h)和V-(b,h)的一些性质,这些性质将用于推导无差异价格的性质.
命题2
(1)U+(θ1, θ2,b,h)与U-(θ1, θ2,b,h)都是(θ1,θ2, b)的凹函数.
(2) 给定b>0, V+(b, h)是h的减函数,而V-(b, h)是h的增函数.
(3) 给定h及实数0<α<1,对任意b>0,式(11)成立
V+(αb,h)≥αV+(b,h)+(1-α)W0,
V-(αb,h)≥αV-(b,h)+(1-α)W0
(11)
证明:(1) 由于效用函数u(x)为其变量x的凹函数,U+(θ1, θ2,b,h)和U-(θ1, θ2,b,h)必定为(θ1, θ2,b)的凹函数.
(2) 对于任意(θ1, θ2),当b>0给定时,目标函数U+(θ1,θ2, b, h)为h的减函数,从而规划的最优值V+(b, h)也是h的减函数.同样由于U-(θ1,θ2, b, h)关于h递增,V-(b, h)是h的增函数.
(3) 首先证明关于V+的不等式.由V+(b, h)和W0分别是(P1)和(P2)的最优解,对任意ε>0,存在(η1, η2)及(ξ1, ξ2)
定义θ1=αη1+(1-α)ξ1, θ2=αη2+(1-α)ξ2,由U+(θ1, θ2,b,h)关于(θ1, θ2,b)的凹性,可以得到
V+(α b, h)≥U+(θ1, θ2,αb,h)=
U+(α(η1,η2,b)+
(1-α)(ξ1,ξ2, 0),h)≥
αU+(η1,η2,b,h)+
(1-α)U+(ξ1,ξ2, 0,h)≥
αV+(b,h)+(1-α)W0-ε
再由ε>0的任意性,V+(αb, h)≥αV+(b, h)+(1-α)W0成立.
同样的方法可以证明关于V-的不等式.
下面讨论无差异价格概念[3-4]在随机区间损益市场下的表现.需要说明的是无差异定价是非线性的定价方法,买入/卖出不同单位数证券所对应的无差异单价是不同的,同样买入/卖出相同单位数证券对应的单价也是不同的.首先给出如下无差异买入价和卖出价的定义.
定义3若h+(b)使得
V+(b, h+(b))=W0
(12)
成立,称h+(b)是投资者买入b单位未定权益X时的无差异买入价;而若h-(b)使得等式
V-(b, h-(b))=W0
(13)
成立,则称h-(b)为投资者卖出b单位未定权益X时的无差异卖出价.
虽然无差异价格与公平价格的定义都是基于期望效用最大化,但是两者的定价机制有不同之处.当市场上仅有基本证券时,投资者只能寻求基本证券构成的最优投资策略.引入未定权益后,投资者有了一个新的投资对象,她/他可以选择买入或者卖空一定单位的未定权益达到最大期望效用.在确定无差异价格的最优化问题中,对未定权益的投资数量是预先确定的,只是寻求基本证券构成的最优投资策略;而在确定公平价格的最优化问题中,对未定权益的投资数量也是一个决策变量,投资者是在寻求基本证券与未定权益构成的最优投资策略.
下面几个命题将讨论无差异价格的存在性及其性质.引入两个量,它们将用于确定无差异价格的范围.记
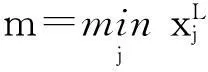
(14)
分别表示未定权益在t=1时刻所有可能状态下的最差和最佳损益表现.
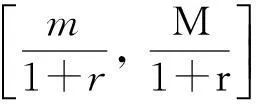
证明:根据最优化理论的最大值定理[15],由效用函数u的连续性,规划的最优值函数V+(b, h)和V-(b, h)都是b和h的连续函数.
对于h-(b),对U-(θ1,θ2, b, h)使用相同的说明方法,
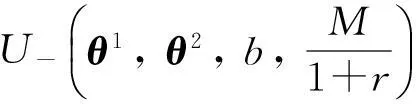
成立,这进一步推出
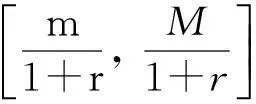
传统的等价鞅测度定价是一个线性定价方法,不管是对未定权益买入还是卖出,也不管交易多少单位,其价格都是一样的.在随机区间损益市场中,由可接受状态价格向量产生的定价结果也是线性的.无差异定价结果是非线性的,未定权益的无差异单价将随着交易单位数的不同而发生变化[3].
命题4若b1>b2,则h+(b1)≤h+(b2)和h-(b1)≥h-(b2)成立.
证明:对b1>b2,存在正数0<μ<1使得b2=μb1.
由式(11),对任何h,成立
V+(b2,h)≥μV+(b1,h)+(1-μ)W0
令h=h+(b2)并利用W0=V+(b2,h+(b2))=V+(b1,h+(b1)),可以得到
W0=V+(b2, h+(b2))≥
μV+(b1, h+(b2))+(1-μ)W0
这表明
V+(b1, h+(b2))≤W0=V+(b1, h+(b1))
利用V+(b,h)关于h的递减性,则h+(b1)≤h+(b2)成立.
对于h-(b)关于b的递增性,再次使用式(11)可以得到对任何h,
V-(b2, h)≥μV-(b1, h)+(1-μ)W0
因此W0=V-(b2,h-(b2))≥μV-(b1,h-(b2))+(1-μ)W0成立,即有
V-(b1, h-(b2))≤W0=V-(b1, h-(b1))
利用V-(b,h)关于h的递增性,则h-(b1)≥h-(b2)成立.
命题4表明,在随机区间损益市场模型下,无差异定价结果也表现出非线性的性质.当投资者购买更多单位未定权益时,期望支付更少的单价;而当投资者卖出更多单位未定权益时,期望获得更多的单价.
下面将讨论对给定的未定权益X,如何计算其无差异价格h+(b),h-(b).在经典随机金融市场模型下,最优期望效用值可以显式表示.在随机区间损益市场模型下,最优期望效用值不能显式表示,因此不能得到无差异价格的显式表达,但是利用数值计算方法,可以轻松地计算两个无差异价格水平.命题3和4给出了无差异价格的范围及其单调性,这使得采用最简单的二分法就可以计算无差异价格.
对于特殊的效用函数u,可以直接计算两个无差异价格水平,并得到具体表达式.在期望效用分析中,最常用的效用函数:对数效用u(x)=lnx,幂函数效用u(x)=xα, 0<α<1,指数效用u(x)=1-e-α x.
对于指数效用u(x)=1-e-α x,U(θ1, θ2),U+(θ1, θ2,b,h)与U-(θ1, θ2,b,h)可以分别表示为
U(θ1, θ2)=1-U′(θ1, θ2)
U+(θ1, θ2,b,h)=1-exp(αb(1+r)h)·
U-(θ1, θ2,b,h)=1-exp(-αb(1+r)h)·
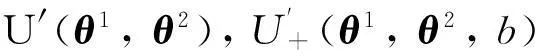
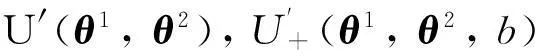
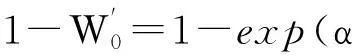
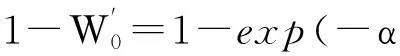
从而有
(15)
以上分析表明在指数效用情形下,未定权益的无差异价格水平可以有直接的表达式.
3算例
考虑一个二叉树市场模型.两个交易日为t=0, 1.假设存在两个可能状态ω1和ω2,发生概率分别为p=P(ω1)=7/12和P(ω2)=1-p=5/12.仅考虑两个基本证券情形.第一种基本证券是债券,t=0时刻的价格为π0=1,为简单起见,设无风险利率为r=0.第二种基本证券为股票,t=0时刻的价格为π1=2,t=1时刻两个状态下的随机区间损益分别为S(ω1)=[3, 4]和S(ω2)=[1, 2].
投资者的效用函数为u=ln(x),悲观度为λ=3/4,初始财富为e=20.首先计算仅投资于基本证券市场所获得的最大加权期望效用值,即下列规划的最优值.
s.t.θ1≥0, θ2≥0
使用Matlab计算可知,规划的最优值为W0=3.0699.
引入损益表现为X(ω1)=[4, 6], X(ω2)=[3/2, 2]的未定权益.规划(P2)和(P3)分别可以表示为
两个规划的最优值分别为V+(b,h)和V-(b,h).预先给出b值,使用二分法可以计算出不同b值所对应的无差异买入/卖出价格,结果如表1所示.
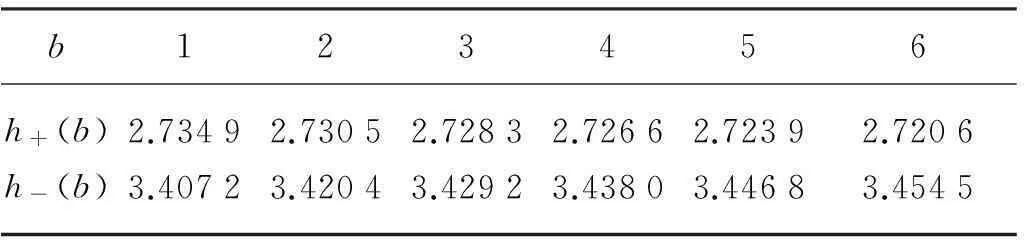
表1 X的无差异买入/卖出价格
4结语
本文将经典随机金融市场模型中的无差异定价方法应用于随机区间损益市场,对有随机区间损益的未定权益进行了定价分析.基于加权期望效用模型,建立了随机区间损益市场模型下的无差异价格概念.讨论了无差异价格的存在性,证明了无差异价格的非线性性质.不同于随机区间损益金融市场模型下的其他定价方法,未定权益的无差异价格将随着交易的单位数发生变化.虽然在随机区间损益市场中,对指数期望效用可以得到无差异价格的显式表达,但是大多数效用函数情形下只能通过数值方法计算无差异价格.后续将研究无差异价格与风险度量之间的关联.
参考文献
[1] HULL J. Options, futures and other derivatives[M]. 7thedition. New-Jersy: Prentice-Hall, 2008.
[2] KARATZAS I, KOU S. On the pricing of contingent claims under constraints[J]. Annals of Applied Probability, 1996, 6(2): 321-369.
[3] CARMONA R. Indifference pricing: Theory and applications[M]. New-Jersy: Princeton University Press, 2009.
[4] MUSIELA M, ZARIPHOPOULOU T. An example of indifference prices under exponential preferences[J]. Finance and Stochastics, 2004, 8(2): 229-239.
[5] MALAMUD S, TRUBOWITZ E, WUTHRICH M. Indifference pricing for CRRA utilities[J]. Mathematics and Financial Economics, 2013, 7(3):247-280.
[6] STOJANOVIC S. Any-utility neutral and indifference pricing and hedging[J]. Risk and Decision Analysis, 2013, 4(2):103-118
[7] RIGOTTI L, SHANNON C. Uncertainty and risk in financial markets[J]. Econometrica, 2005, 73(1): 203-243
[8] HUANG X X. Minimax mean-variance models for fuzzy portfolio selection[J]. Soft Computing-A Fusion of Foundations, Methodologies and Applications, 2010, 15(2): 251-260.
[9] YU S, HUARNG K, LI M. A novel option pricing model via fuzzy binomial decision tree[J]. International Journal of Innovative Computing, Information and Control, 2011, 7(2): 709-718.
[10] MUZZIOLI S, TORRICELLI C. A multiperiod binomial model for pricing options in a vague world[J]. Journal of Economic Dynamics & Control, 2004, 28(5): 861-887.
[11] YOU S R, LE J J, DING X D. Pricing a contingent claim with random interval or fuzzy random payoff in one-period setting[J]. Computers & Mathematics with Applications, 2008, 56(8): 1905-1917.
[12] YOSHIDA Y, YASUDA M, NAKAGAMI J, et al. A new evaluation of mean value for fuzzy numbers and its application to American put option under uncertainty[J]. Fuzzy Sets and Systems, 2006, 157(19): 2614-2626.
[13] YOU S R, PENG Y Z, ZHAO F F. On utility maximization with random interval payoffs[J]. Chinese Quarterly Journal of Mathematics, 2012, 27(3): 424-431.
[14] YOU S R, SHI J Y. On fair prices of a contingent claim with random interval payoff[J]. Journal of Donghua University(English Edition), 2013, 30(2): 153-157.
[15] OK E A. Real analysis with economic applications[M]. New-Jersy: Princeton University Press, 2007.
Indifference Prices of Contingent Claims in a Market of Securities with Random Interval Payoffs
YOUSu-rong,WEIKang
(College of Science, Donghua University, Shanghai 201620, China)
Abstract:Based on weighted expected utility maximization, definitions of indifference bid and ask prices to a contingent claim with interval payoff are proposed. Existence and properties of two prices are discussed. Applying the method of bisection, a simple binomial tree model is given as an example to calculate indifference prices.
Key words:contingent claim;random interval;expected utility;indifference pricing
中图分类号:O 29;F 224
文献标志码:A
作者简介:尤苏蓉(1976—),男,江苏靖江人,副教授,博士,研究方向为金融数学.E-mail: sryou@dhu.edu.cn
基金项目:中央高校基本科研业务费专项资金资助项目
收稿日期:2014-11-10
文章编号:1671-0444(2016)01-0145-07
