考虑风险态度的双渠道供应链协同优化决策
2016-04-20刘峥,徐琪
刘 峥, 徐 琪
(1. 上海工程技术大学 管理学院,上海 201620; 2. 东华大学 旭日工商管理学院,上海 200051)
考虑风险态度的双渠道供应链协同优化决策
刘峥1, 徐琪2
(1. 上海工程技术大学 管理学院,上海 201620; 2. 东华大学 旭日工商管理学院,上海 200051)
摘要:双渠道供应链成员的风险态度将对渠道优化运作产生重要影响.考虑双渠道订货提前期重叠时可能产生的供货风险,通过引入网络渠道替代效应因子和制造商为零售商承担促销成本比例因子,建立了双渠道供应链协同决策基础模型.在此基础上,针对双渠道供应链成员的风险态度为中性或规避情形,建立了协同决策下的最优定价模型和期望利润模型,并通过算例验证模型的可行性.
关键词:双渠道供应链; 优化决策; 供应链风险; 风险态度
随着网络技术的飞速发展,传统企业的营销模式也发生了巨大转变.制造商为提高产品市场占有率,增强企业竞争力,拓展了多种营销渠道.传统零售渠道与网络直销渠道并存的渠道结构(即双渠道供应链模式)是目前普遍存在的销售模式.双渠道供应链模式在为制造商和零售商带来机遇的同时存在诸如库存、协调等风险.如何通过有效合作及合理的定价策略规避或降低双渠道供应链的风险,已成为近年来供应链管理领域的一个重要研究内容,学者们已做了许多有益的探讨.
例如,文献[1]在需求具有价格敏感性条件下,构建了收益共享契约模型,提出了零售商分享制造商网络渠道部分利润的逆收入共享策略.文献[2]给出了双渠道零售商的均衡利润、电子商务渠道和传统渠道的最优定价、电子商务消费者和传统消费者的构成情况.文献[3]探讨了供应链渠道的结构与协调的关系,设计了惩罚契约和补偿-委托契约进行协调.文献[4]建立了因突发事件导致的市场需求和渠道流通过程的损耗比例同时发生扰动状态时的市场需求模型,求出了最优渠道销售价格、销售数量以及生产数量,并设计了收益共享契约协调下的双渠道供应链.文献[5]综合考虑了供应链成员的风险态度,在双渠道的二级供应链模型的基础上,比较了电子渠道单独由制造商控制的竞争模式和制造商与零售商的合作模式,得到了制造商与零售商采取合作模式的解析条件.文献[6]构建了基于供应商和零售商共同分担服务成本的供应链协调机制,以促进零售商服务水平的提高,并改善供应链整体绩效和参与双方的利润.文献[7]默认供应链双方是风险中性的,对逆收入共享策略来协调渠道冲突这种合作模式和传统模式进行了比较分析.文献[8]针对具有风险规避特征的制造商和零售商组成的双渠道供应链,分析非竞争环境下双渠道供应链中产品在不同渠道的最优定价.文献[9]构建了基于双渠道的二级供应链模型,在考虑供应链双方的风险态度基础上得到了制造商和零售商采取合作模式的解析条件.文献[10-11]研究了风险规避特征的制造商和零售商参与的双渠道供应链的最优策略问题,以及市场需求方差对最优决策的影响.
现有的文献多从渠道协调角度着手,结合风险态度下的制造商和零售商行为特点,运用博弈理论构建契约模型,以期求得双渠道供应链中产品在不同渠道下的最优定价策略,而对于订货提前期重叠对供应链的影响则鲜有涉及.本文考虑两个渠道订货提前期重叠时将可能产生供货风险,首先建立了制造商承担部分零售商的促销服务投入成本的双渠道协同合作模型,进而考虑两个渠道成员的风险态度,建立了不同风险态度下的双渠道供应链协同定价和利润模型,最后进行了仿真计算与分析.
1问题描述及模型假设
1.1问题描述与模型符号
本文考虑由单一零售商构成的零售渠道和一个制造商主导的网络渠道构成的双渠道供应链系统.在该系统中,一方面零售商从制造商处批发产品,并销售至终端顾客;另一方面,制造商在批发给零售商产品的同时,通过自行开设的网络渠道直接向终端客户销售产品,模型中所涉及的变量表示如下:
Em为制造商的期望收益;
Er为零售商的期望收益;
Ej为协同订货策略下供应链的期望收益;
ri为网络渠道的单位缺货成本;
rr为零售渠道的单位缺货成本;
sr为零售渠道的单位货品残值;
si为网络渠道的单位货品残值;
Qr为零售渠道的订货量;
xi为网络渠道面临的市场需求;
xr为零售渠道面临的市场需求;
y为重叠时间(y≤0表示制造商在提前期内按时送货,y>0表示制造商送货延迟y个周期);
μ为提前期内订货重叠的概率密度函数服从正态分布的期望;
δ为提前期内订货重叠的概率密度函数服从正态分布的标准差;
a为市场需求的期望;
t为制造商单位产品生产成本;
w为提前期重叠时对两个渠道期望利润产生的影响因子;
pi为网络渠道的单位产品售价;
pr为零售渠道的单位产品售价;
c为制造商向零售商供货时的单位产品售价;
h为单位产品单位时间的持有成本;
k为零售商的促销服务所投入的成本.
1.2模型假设
为确保所构建模型有意义,本文有如下假设:
(1) 为确保双渠道供应链协同定价顺利进行,假定Em和Er均为正;
(2) 假设网店与零售店所面临的市场需求为随机变量;
(3) 设订货周期的基准时间为0,若制造商在提前期内按时供货,用y≤0表示;若制造商延期供货时,用y>0表示延迟的时间.
1.3基础模型
由于供应链双渠道环境中存在着需求不确定、供货不及时等风险,如两个渠道间缺少合作时,可能产生两个渠道的订货提前期出现相互重叠的情况,此时,制造商的生产能力需要同时满足两个渠道的订货要求,如果不能及时满足,则会导致两个渠道的供货风险.而且,如果订货量大于市场需求,供应链又会面临囤货风险.因此,两个渠道的协同决策是很重要的.
这里讨论的基础模型主要考虑双渠道供应链成员无风险偏好和风险规避情况下的一般模型.在该模型中通过引入网络渠道替代效应因子和制造商为零售商承担促销成本比例因子来实现协同.
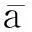
为了实现供应链协调共赢,两个渠道采用协同合作模式.该模式是制造商在促销服务中承担部分零售商的促销服务的投入成本,从而给零售商提供部分补偿,弥补因网络渠道的加入引起的需求转移带来的损失.若零售商促销服务中的成本为k,设促销服务投入成本分摊比例为f,其中f∈(0, 1),则制造商承担f·k促销服务费用.
供应链双方为Stackelberg主从博弈,制造商首先宣布产品的批发价格c和促销服务费用分摊比例f及网络渠道价格pi,然后,零售商确定零售价格pr和促销服务投入成本k.制造商的利润由网络渠道获得的利润和销售给零售商产品赚取的利润两部分构成.制造商和零售商的收益函数分别为
πm=(pi-t)xi+(c-t)xr-f·k
(1)
πr=(pr-c)xr-(1-f)k
(2)
根据逆向归纳法求解该Stackelberg均衡,首先在假定批发价格c和促销服务费用分摊比例f及网络渠道价格pi已知的情况下,求解第二阶段零售商的反应函数.
为了便于比较协同决策的效果,考虑制造商和零售商渠道订货提前期不重叠及重叠情况,建立制造商和零售商的独立定价模型,据此,可以分别得出制造商和零售商的决策方案.
(1) 制造商独立定价:
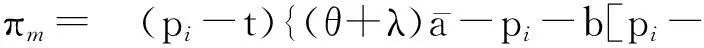
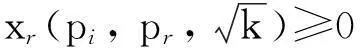
(3)
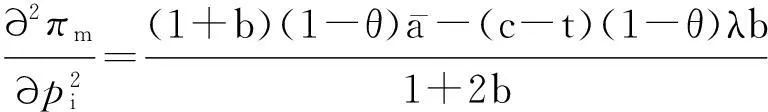
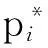
(4)
(2)零售商独立定价:
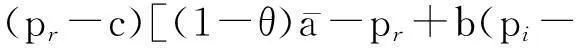
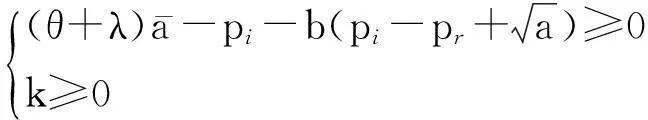
(5)
对目标函数中的pr求一阶导数,可得:
(6)
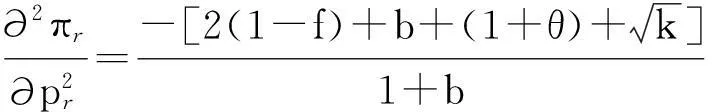
2风险中性态度下的模型构建
2.1供应链双渠道协同定价模型
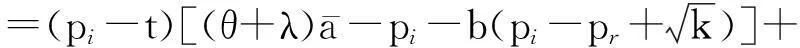
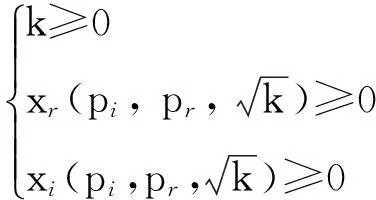
(7)
考虑所有约束大于0时,对该问题进行求解,可得:
(8)
(9)
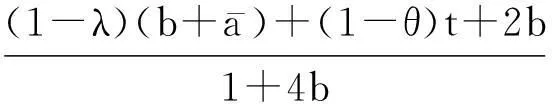
2.2协同决策下的供应链期望利润模型

(10)
3风险规避态度下的双渠道供应链优化
在两个渠道持风险规避态度时,双方更倾向于采取协同策略规避风险.类似的,双方以供应链整体利益最大化来决策,通过供应链激励策略,实现协同合作.zr和zi分别表示制造商和零售商的风险态度,z=0表示风险态度为中性,z<0表示决策者为风险偏好,z>0表示风险规避态度,z越大,决策者越不愿意面对风险的影响.
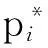
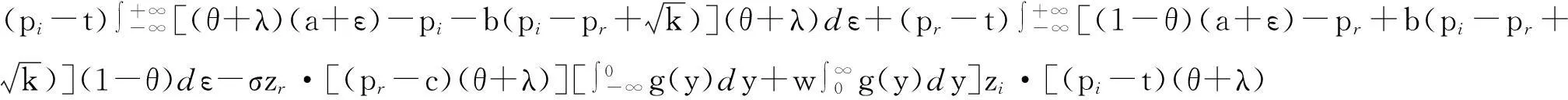
(11)
4算例仿真及模型分析
假定在一个由若干同质零售店和一个由制造商管控下的网络渠道构成的系统中,限定各参数范围,参数从离散的数据中取值.各参数范围如下:
μ∈(0, 1, 2, 3, 4, 5, 6, 7, 8, 9);
δ∈(0, 1, 2, 3, 4, 5, 6, 7, 8, 9);
c∈(12, 17, 22, 27, 32, 37, 42, 47);
h∈(0.001t)
c∈(12, 17, 22, 27, 32, 37, 42, 47);
rr, ri∈(0.18t, 0.23t, 0.28t, 0.33t);
si, sr∈(0.15t, 0.35t, 0.50t, 0.65t);
t∈(18, 23, 28, 33);
α∈(100, 200, 300, 400);
θ, λ, b, f, ω∈(0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9,1.0);
ε∈(12, 22, 32, 42);
k∈(10).
4.1风险中性态度下的供应链协同定价
在双渠道供应链协同定价情形下,双方能够从整体最优的角度确定双方的最优定价,进而使整体收益最大化.
当双渠道供应链成员实施协同决策时,制造商网络渠道和零售渠道的最优定价pi和pr随着网络渠道的需求比例θ和零售渠道新增市场需求比例λ的变化如图1所示.由图1可知,若λ一定时,pr随着θ的增加而增加,pi随着θ的增大而降低;当θ和λ取特定值时,pr与pi相等.由此说明,网络渠道的出现会造成需求重构,进而使得两个渠道的定价策略随着改变.相似的,零售渠道的订货量Qr随着θ以及λ的变化如图2所示.由图2可知,当θ一定时,订货量Qr随着λ的增加而下降;当λ一定时,订货量Qr随着θ的增加而增加.
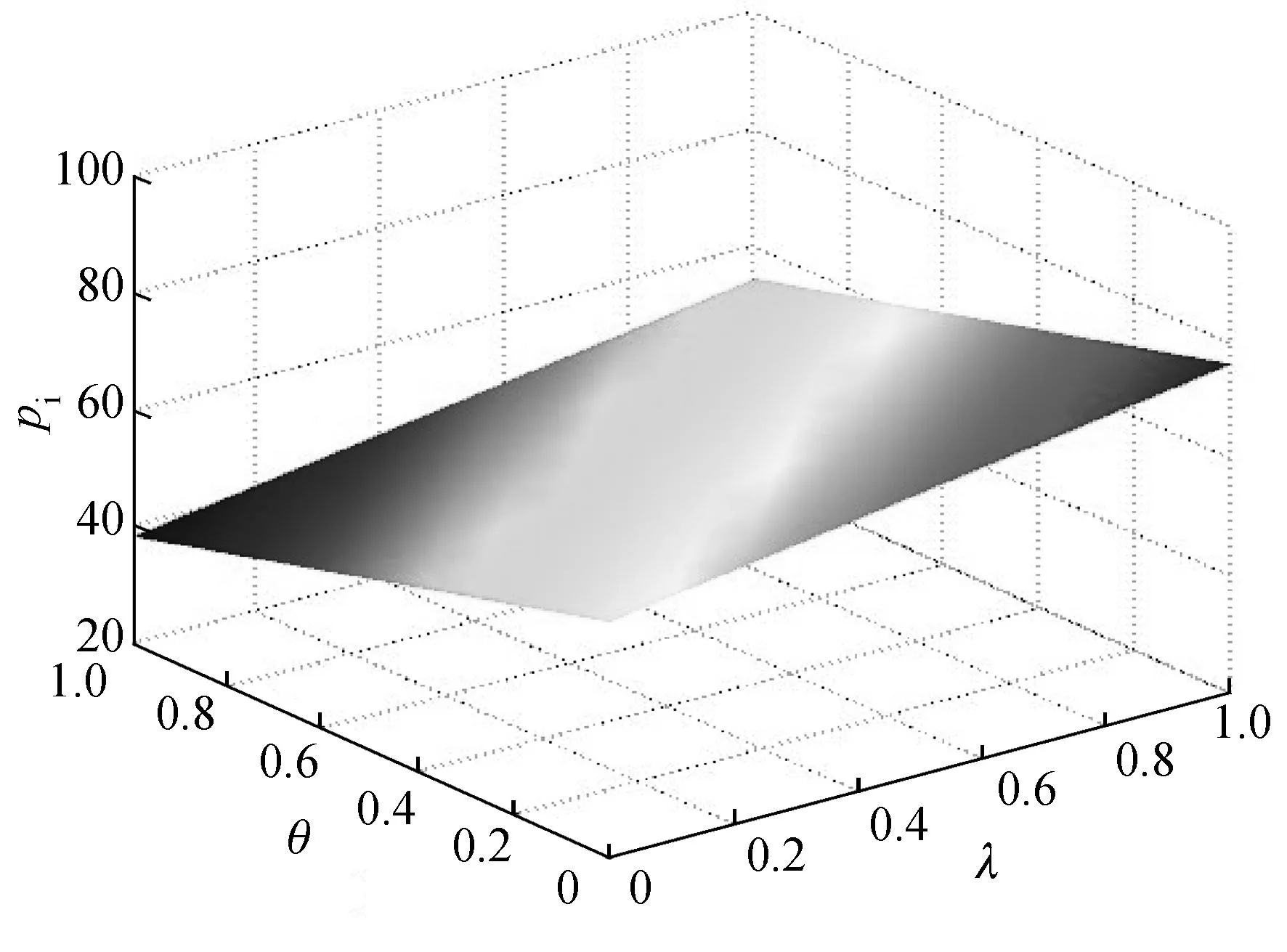
(a) pi
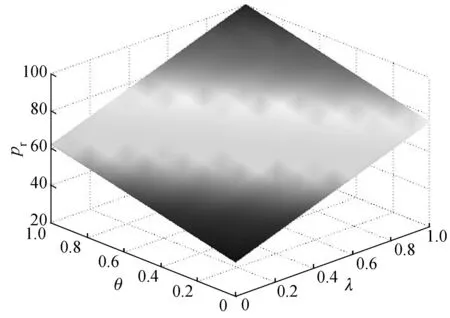
(b) pr
Fg.1piandprchanges withθandλ
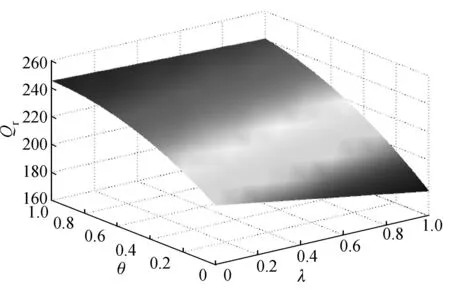
图2 Qr随θ和λ的变化Fig.2 Qr changes with θ and λ
4.2风险规避态度下的供应链协同定价
在供应链成员为风险规避且制造商和零售商间存在协同机制时,两个渠道从整体最优的角度确定双方的最优定价,促使整体收益最大化.
在供应链成员风险规避态度下,当协同决策时,制造商网络渠道和零售渠道的最优定价pi和pr随着网络渠道替代零售渠道的效应因子b和提前期重叠影响因子w的变化如图3所示.由图3可知,当w一定时,pi随替代效应因子b的增加而提高,而pr则随着w和b的增大而降低,并与pi交会.这说明随着网络渠道客户的增加,原本零售渠道的顾客向网络渠道部分转移,零售商将通过提高售价来增加收益.相似的,当w和b呈下降趋势时,pr也会逐步提高.
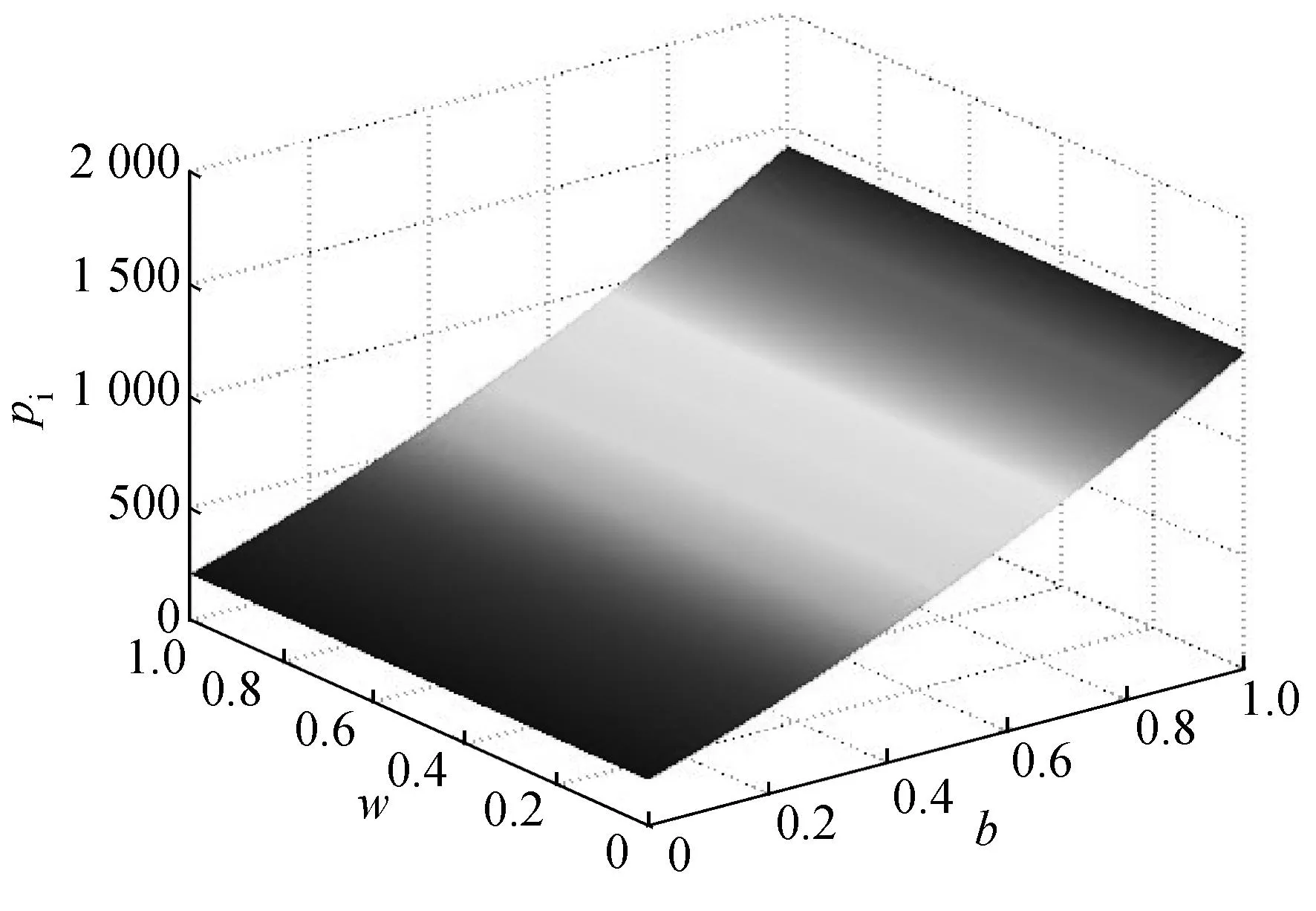
(a) pi
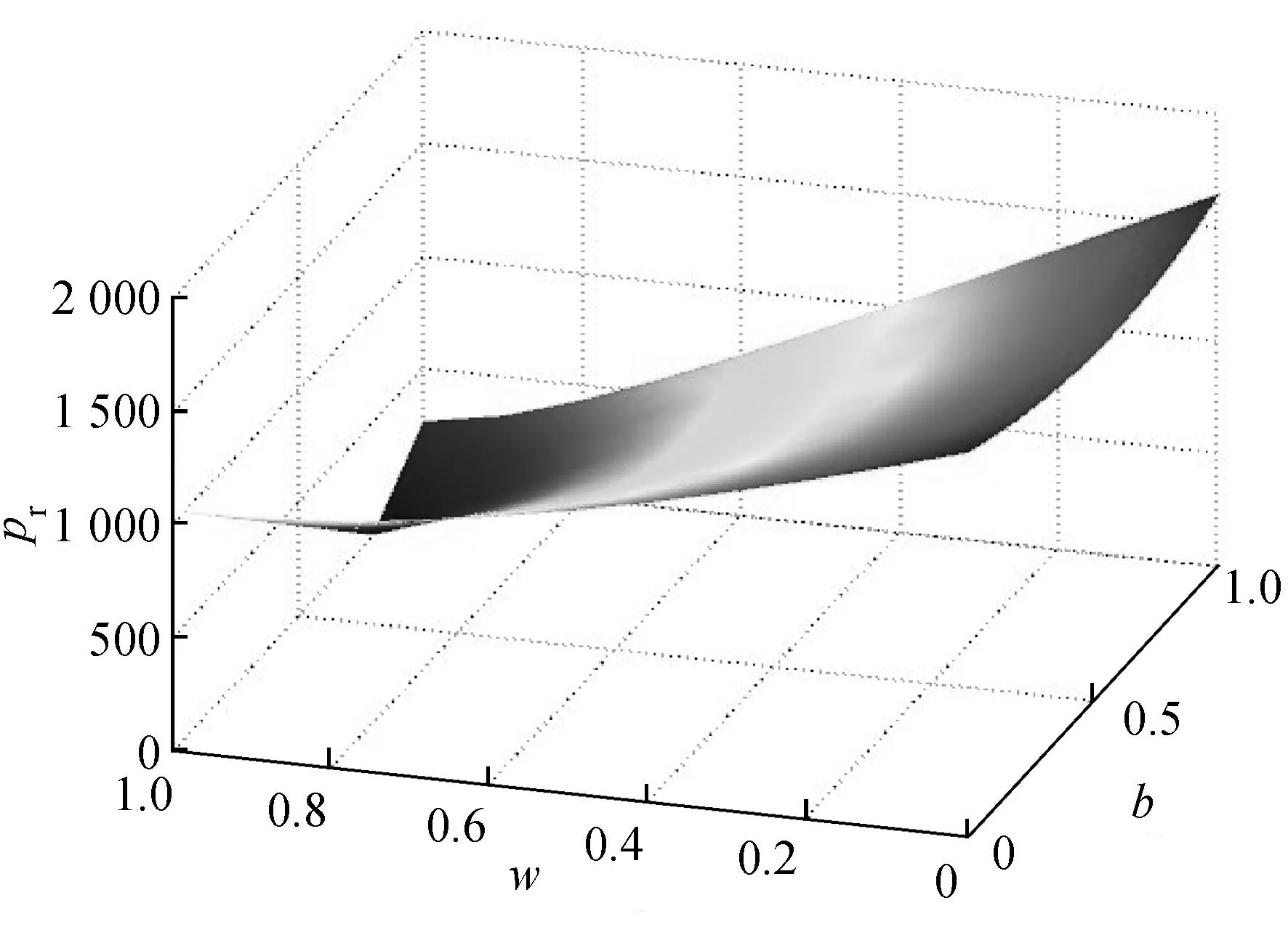
(b) pr
Fig.3piandprchanges withwandb
当供应链成员实施协同决策时,零售渠道的订货量Qr随市场规模α和需求波动系数ε的变化如图4所示.
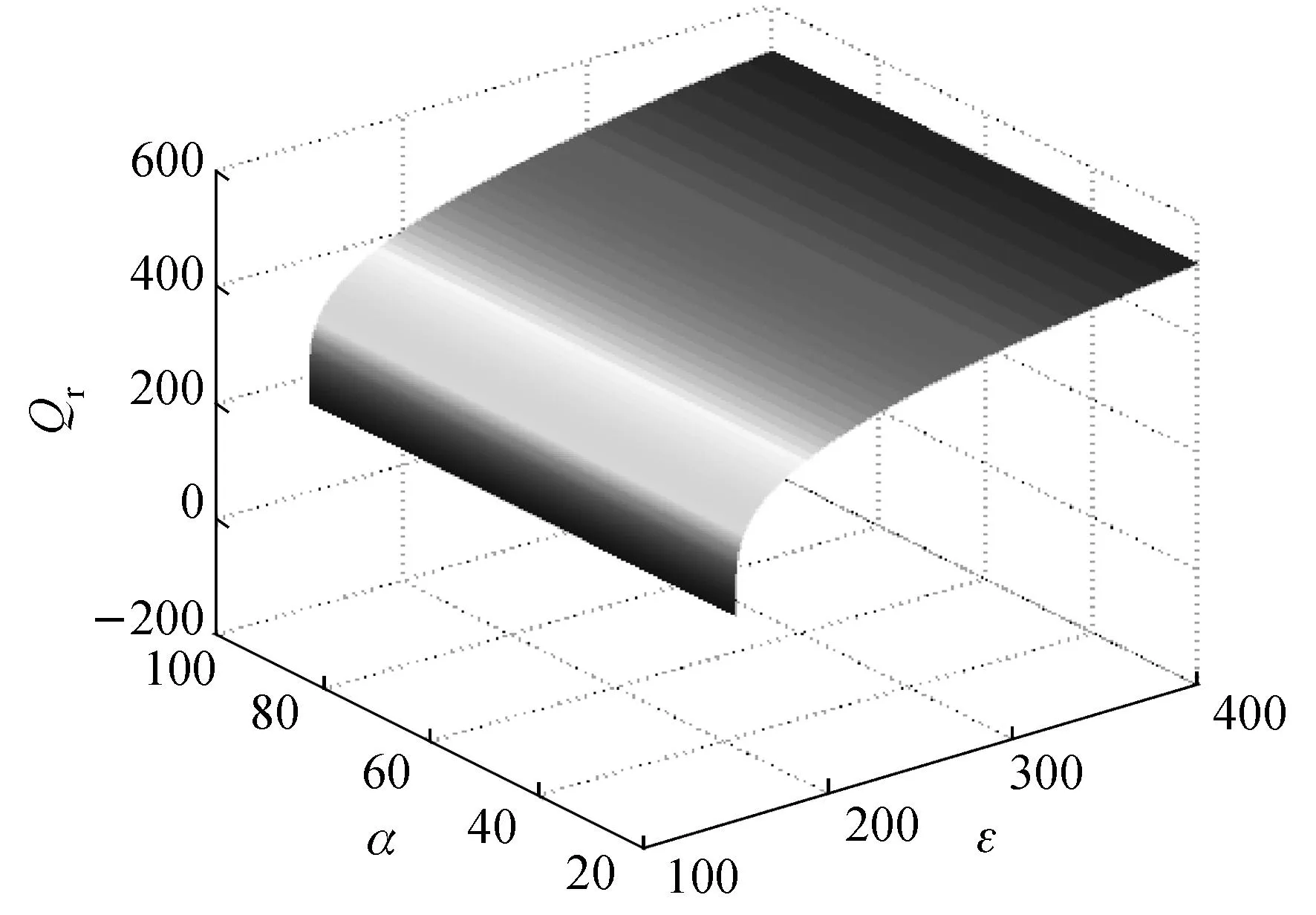
图4 Qr随α和ε的变化Fig.4 Qr changes with α and ε
由图4可知,当市场需求波动ε相对稳定,随着市场规模α的增大,零售渠道的订货量会相应增加;而当市场规模α相对固定时,零售渠道的订货量会随着需求波动ε的增加而增加,通过增大订货量来降低因波动引起的缺货风险.
4.3风险中性与风险规避态度下绩效比较
在风险中性和风险规避态度下,零售商、制造商、供应链系统期望收益以及协同条件下供应链期望收益如表1所示.由表1可以看出,风险中性下的制造商、零售商的期望收益要高于风险规避下制造商、零售商的期望收益.这说明,由于存在风险防范意识,风险规避者往往不会通过大量囤货来满足市场需求,此举在降低库存成本的同时也丧失了满足市场需求的机会.而另一方面,当实施协同定价策略时,风险规避下的协同供应链期望收益要高于风险中性下的协同供应链期望收益,可以得出,双渠道供应链协同定价策略对于风险规避情形更加有效,能够有效地防范风险.因此,对风险承受力越低的供应链企业越是应该采取协同定价策略,实施供应链协同定价策略能够更好地提高盈利水平,实现两渠道双赢.
表1风险中性和规避态度下零售商、制造商及
协同供应链期望收益比较
Table 1Comparison of the expected benefit of retailers, manufacturer and collaborative supply chain under the neutral and aversion risk attitude
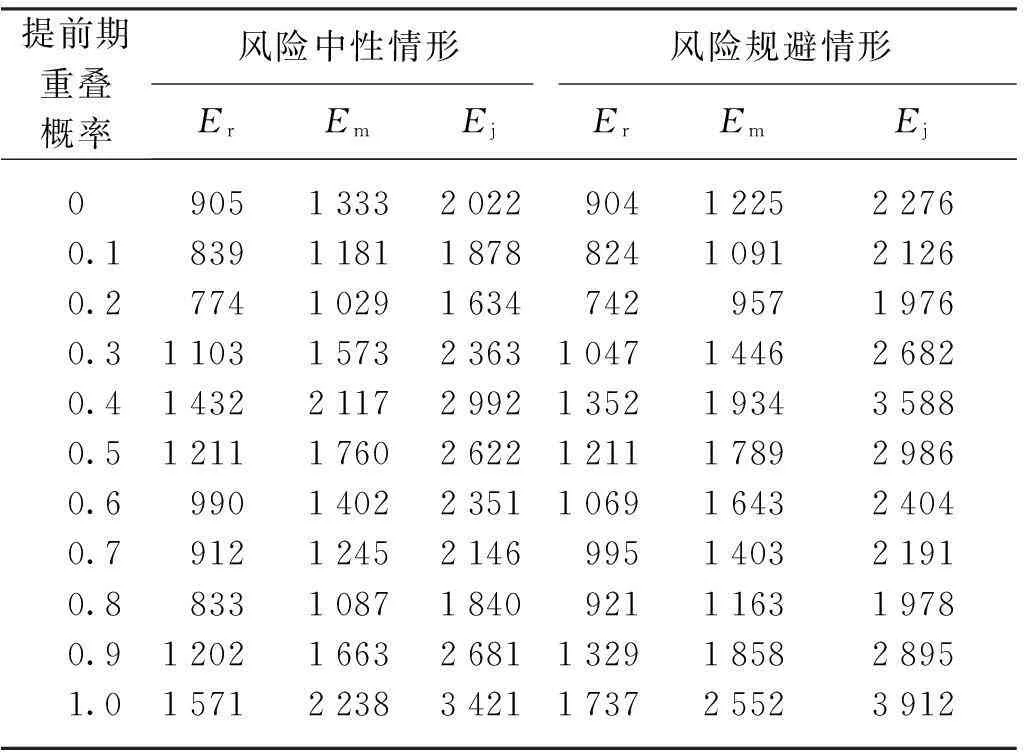
提前期重叠概率风险中性情形风险规避情形ErEmEjErEmEj090513332022904122522760.183911811878824109121260.27741029163474295719760.31103157323631047144626820.41432211729921352193435880.51211176026221211178929860.6990140223511069164324040.791212452146995140321910.883310871840921116319780.91202166326811329185828951.0157122383421173725523912
5结语
在双渠道分销系统中,制造商不但作为零售商的供应商,同时也作为零售商的直接竞争者存在,这样供应链的成员将面临各类供货、积压等风险,渠道对风险所持态度的不同对供应链的运作产生重要影响.本文考虑双渠道供应链中制造商和零售商的风险态度,探讨了制造商和零售商两个渠道的最优定价以及协同下的利润分配问题.利用数值仿真分析,进一步验证了风险态度对供应链双方利润和定价的影响,可以得到如下结论和启示:
(1) 在风险规避情形下,若双方实施协同定价决策时,两个渠道以供应链整体利益最大化为目标,得到Pareto定律最优定价.当制造商网络渠道替代性增强时,两个渠道提前期供货冲突几率增加时,制造商会提高网络渠道产品售价以尽可能获得盈利,而零售商则会降低零售渠道售价以吸引部分客户,最终促使一部分利润从网络渠道分流给零售渠道,以确保供应链整体及各自渠道的利润最优.零售渠道的订货量随市场规模和需求波动系数的变化而变化,当市场规模相对固定时,零售渠道的订货量会随着需求波动的增加而增加,通过增大订货量来降低因波动而引起的缺货风险.
(2) 对比风险中性和风险规避态度下两渠道及供应链收益情况,可以发现持风险规避态度的成员在规避了风险的同时也失去了一定的获利机会,如果能够合理制定协同定价策略,那么两个渠道及系统的利润可以高于持风险中性时两个渠道各自的利润,说明当两个渠道持风险规避态度时,更适合采取协同策略.
参考文献
[1] 徐广业,但斌,肖剑.基于改进收益共享契约的双渠道供应链协调研究[J].中国管理科学,2010,18(6):59-64.
[2] 陈云,王浣尘,沈惠璋.互联网环境下双渠道零售商的定价策略研究[J].管理工程学报,2008,22(1):34-39.
[3] 但斌,徐广业,张旭梅.电子商务环境下双渠道供应链协调的补偿策略研究[J].管理工程学报,2012,26(1):125-130.
[4] 吴晓志,陈宏,张俊. 需求和路途损耗扰动下双渠道供应链的应急决策[J].技术经济,2014,33(8):120-127.
[5] 李书娟,张子刚,黄洋.风险规避对双渠道供应链运作模式的影响研究[J].工业工程与管理,2011,16(1):32-36.
[6] 罗美玲,李刚,孙林岩.具有服务溢出效应的双渠道供应链竞争[J].系统管理学报,2011,20(6):648-657.
[7] ZHU L, HONG K S, LEE C. Optimal ordering policy of a risk-averse retailer subject to inventory inaccuracy [J]. Mathematical Problems in Engineering, 2013, 1(1):1-9.
[8] CHERNONOG T, AVINADAV T. Profit criteria involving risk in price setting of virtual products [J]. European Journal of Operational Research, 2013, 236(1):351-360.
[9] YOO S H. Product quality and return policy in a supply chain under risk aversion of a supplier [J]. International Journal of Production Economics, 2014, 154:146-155.
[10] 王虹,周晶.具有风险规避参与者的双渠道供应链最优策略研究[J].计算机集成制造系统,2009,15(11):32-36.
[11] 王虹,周晶.竞争和风险规避对双渠道供应链决策的影响[J].管理科学,2010,23(1):10-17.
Dual-Channel Supply Chain Collaborative Optimal Strategies Based on Risk Attitudes
LIUZheng1,XUQi2
(1.SchoolofManagement,ShanghaiUniversityofEngineeringScience,Shanghai201620,China;2.GloriousSunSchoolofBusinessandManagement,DonghuaUniversity,Shanghai200051,China)
Abstract:Risk attitude of partners in dual-channel supply chain system exerts a major impact on channel optimization. By consideration of delivery risk caused by lead time overlap, through introduction of online channel substitution effect factor and ratio factor that manufacturer bears promotional cost for retailers, dual-channel supply chain collaborative decision-making model is developed. On this basis, for supply chain members who have neutral attitude or aversion risk, the optimal pricing model and expected profit model based on collaborative decision-making have been developed, followed by verification of feasibility through a numerical example.
Key words:dual-channel supply chain; optimal strategy; supply chain risk; risk attitude
中图分类号:F 270.7
文献标志码:A
作者简介:刘峥(1987—),男,天津人,讲师,博士,研究方向为供应链和物流管理.E-mail:liuzheng960@163.com徐琪(联系人),女,教授,E-mail:xuqi@dhu.edu.cn
基金项目:国家自然科学基金资助项目(715572033, 71172174, 71502101);国家社会科学基金青年资助项目(CJY014);上海市教委科研创新重点资助项目(13ZS129);上海高校青年教师培养资助计划项目(ZZGCD15014);上海工程技术大学博士启动基金资助项目(校启2015)
收稿日期:2014-12-16
文章编号:1671-0444(2016)01-0098-06
