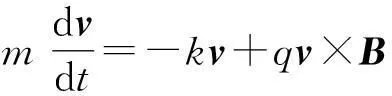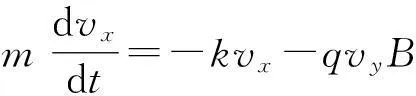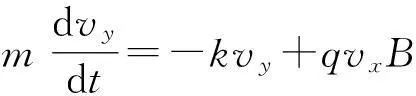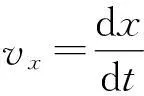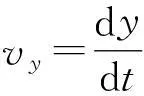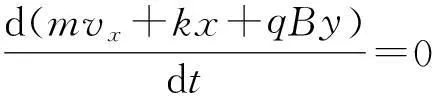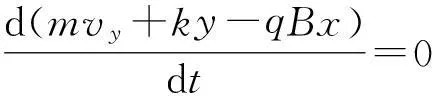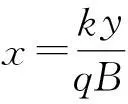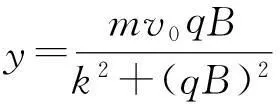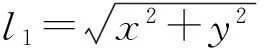例谈复合场中的守恒量

涂德新

(江西师范大学附属中学　江西 南昌　330046)



例谈复合场中的守恒量

涂德新

(江西师范大学附属中学江西 南昌330046)

摘 要：通过对3个复合场中守恒量的寻找和处理，体现某些物理量的特点，直观展示物理变化过程中的规律，这对我们平时分析和研究物理问题或许有一定的借鉴.

关键词：微分复合场洛伦兹力守恒量

动量守恒定律、角动量定恒定律和能量守恒定律是物理学中的三大守恒定律.守恒定律不仅适用于宏观物体的运动，也适用于微观粒子的运动；不仅适用于低速物体的运动，也适用于高速物体的运动，也就是说在牛顿运动定律不再适用的领域它们仍然有效，这已经为近代物理学研究的大量实践所证明.守恒定律中的守恒量是对物理现象最简洁的表述，笔者发现在一些复合场(重力场、电场、磁场等)中，带电粒子的运动也有一些守恒量，下面通过几个情景的分析和处理初步研究此问题.

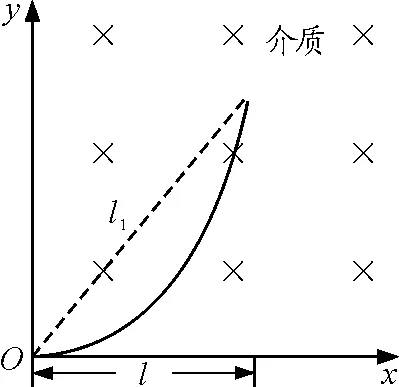
情景1：一电容器左右极板间电压为u，极板间距为d，速度为零的电子(质量为m，电荷量为e)，由电容器左极板的小孔O处，在电场力的作用下加速，同时在垂直纸面向外的匀强磁场B的作用下偏转.

问题：求电子不能到达右极板时匀强磁场B的最小值.

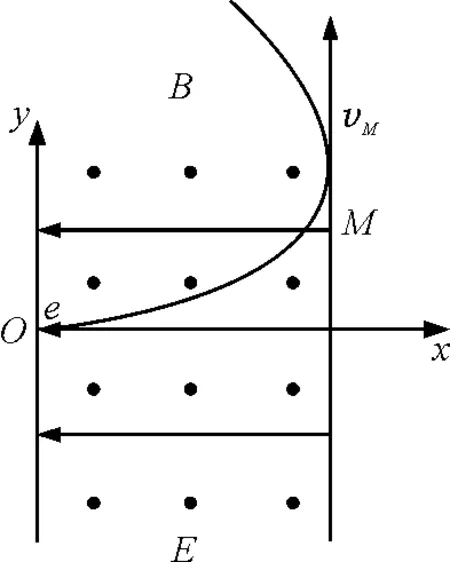
图1

解析：如图1所示，假设图中电子的一条运动轨迹正好与右极板相切，此时所对应的匀强磁场B的值就是本题所求的最小值.

在此轨道上任取一点(x,y)，写出y方向的动力学方程.

注意到洛伦兹力在y方向的分力是由x方向的分速度引起的，即

may=evxB

(1)

同时

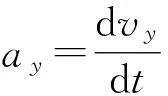
(2)

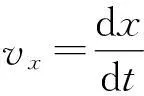
(3)

由式(1)～(3)得

这就得到了一个守恒量mvy-eBx.

联系初始点和与右极板相切的点M，写出方程

0=mvM-eBd

(4)

利用电场力做功，得到vM满足的关系式

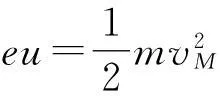
(5)

由式 (4)、(5)可得

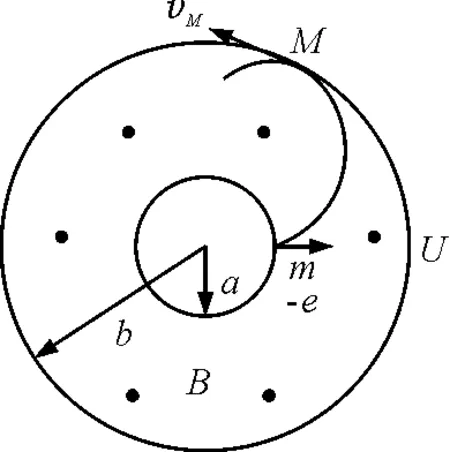
情景2：如图2所示，半径分别为a和b(a

图2

问题：电子刚好到不了外筒，求此时磁感应强度B的值.

解析：对电子写出角动量定理

(6)

在电子的轨道上任取一点，该点离柱轴的距离为r，洛伦兹力存在角向分力，这个分力是由电子的径向速度引起的，即

Fθ=evrB

相应的力矩为

Fθr=evrBr

(7)

由式(6)、(7)得

(8)

注意到

(9)

联立(8)、(9)可得

联系最初的出发点与相切点M，可得

(10)

利用电场力做功，得到vM满足的关系式

(11)

由式(10)、(11)可得

情景3：如图3所示，带电粒子进入介质，受到与它的速度方向相反且成正比的阻力作用，在粒子停下来时，通过的距离l=10 cm.如果在介质中有跟粒子进入速度方向相垂直的匀强磁场，而粒子仍以原来的速度进入介质，停止时与入射点相距l1=6 cm.

图3

问题：如果磁感应强度B减弱为一半，那么该粒子应停在离入射点多远处？

解析：设带电粒子在介质中受到的阻力为f=-kv(k为正的常量),无磁场时，对带电粒子写出牛顿第二定律

(12)

注意到

(13)

由式(12)、(13)得

得到一个守恒量mv+kx.

联系最初和最终有

mv0=kl

于是

(14)

有磁场时写出牛顿第二定律

(15)

由式(15)写出x,y方向的分量方程

(16)

(17)

注意到

(18)

(19)

由式(16)～(19)得

(20)

(21)

由式(20)和(21)可得守恒量

mvx+kx+qBy

以及

mvy+ky-qBx

联系最初和最终有

mv0=kx+qBy

(22)

0=ky-qBx

(23)

由式(22)及式(23)可以解得

(24)

(25)

同时距离

(26)

由式(14)、(24)～(26)可得

(27)

同理，磁感应强度B减半时有

(28)

联立式 (27)、(28) 可以求解得

l2=8.3 cm

可以分析到3种情况下轨迹的长度是一样的，原因是均只有阻力做功.

小结：物理学家在研究一些待认识的问题时，常常是想方设法找到所研究的现象中是否存在某种不变量，即某些物理量是守恒的情况，并总结出动量、角动量和能量的守恒定律.

我们在研究物理情景和物理问题时，也可以发现一些守恒量，只要过程满足一定的条件，就可以不必考虑过程中的细节，而对系统的初末状态的某些物理量作出某种结论，这是守恒量的特点,也是它们的优点.

Talking about the Case of Conservation Quantities in the Compound Fields

Tu Dexin

(Affiliated High School of Jiangxi Normal University, Nanchang,Jiangxi330046)

Abstract:In this paper, based on the three compound field keep constant finding and treatment, reflect the characteristics of certain physical quantities, intuitive display of a physical change in the rules, which we usually analysis and research on the physics problem may have certain reference.

Key words:differential; compound field; Lorentz force; conservation quantity

(收稿日期：2015-12-02)