Novel SCNS/RSINS tight-integrated alignment based on adaptive interacting multiple model filters on shipboard

ZHOU Ling-feng, DONG Yan-qin, ZHAO Wang-yang, ZHAO Xiao-ming, QU Yuan-jin, HOU Zhi-ning

(1. College of Automation, Harbin Engineering University, Harbin 150001, China; 2. Equipment Academy of the Rockets Force, Beijing 100092, China; 3. Tianjin Navigation Instrument Research Institute, Tianjin 300131, China)

Novel SCNS/RSINS tight-integrated alignment based on adaptive interacting multiple model filters on shipboard

ZHOU Ling-feng1,3, DONG Yan-qin2, ZHAO Wang-yang3, ZHAO Xiao-ming1,3, QU Yuan-jin3, HOU Zhi-ning3

(1. College of Automation, Harbin Engineering University, Harbin 150001, China; 2. Equipment Academy of the Rockets Force, Beijing 100092, China; 3. Tianjin Navigation Instrument Research Institute, Tianjin 300131, China)

In order to improve the accuracy and rapidity of initial alignment for shipboard single-axis Rotation Strapdown Inertial Navigation System (RSINS), an Adaptive Interacting Multiple Model (AIMM) alignment method is applied into Strapdown Celestial Navigation System (SCNS)/RSINS tight integrated navigation system. The AIMM algorithm combines the IMM algorithm with the improved Sage-Husa adaptive filtering algorithm, which can achieve the coverage of real situation through a few sub-models. The complementary navigation information is provided by different kinds of sensors, which can overcome such problems as the single sensor’s low accuracy and traditional extended Kalman filter’s linearization errors, so the accuracy of the SCNS/RSINS integrated navigation system can be significantly improved. The proposed AIMM alignment algorithm utilizes two parallel filters, in which the state and observation models are established reasonably: the first filter is based on attitude quaternion algorithm, its measurement equation is formed from the difference between SCNS’s and RSINS’s attitude quaternion; and the second filter is based on the errors characteristics of SCNS and RSINS, its measurement equation is formed from the difference between SCNS’s and RSINS’s position and heading. Then an Adaptive Interacting Multiple Model Filter (AIMMF) algorithm is applied to process the above two parallel filters’ data. To some extent, the performance of EKF will be degraded due to the uncertainty of the process and measurement noises. By means of a model switching mechanism, the IMM can be utilized for selecting an appropriate model automatically and calculating the process noise covariance in alignment phase. The resulting sensor fusion algorithm can effectively solve the alignment problem for the SCNS/RSINS integrated navigation system. Finally, the proposed AIMMF algorithm is testified by simulations, which show that the estimation accuracy and alignment rapid capacity are improved compared with those of the extended Kalman filter algorithm.

SCNS/RSINS integrated navigation system; extended Kalman filter; adaptive interacting multiple model filter algorithm

1 Introduction

The inertial navigation system (INS) has been widely used due to its advantages of autonomy, concealment, continuum and independence. As we know, the accuracy of initial alignment has significant impact on the navigation accuracy of INS. An inaccurate alignment will degrade the navigation accuracy directly[1]. However, the INS’s alignment accuracy can be improved by the information from some other navigation sensors, such as SCNS[2].

SCNS can provide high-accuracy attitude information in i-frame independently, as a high-precision attitude measuring device, it can also provide position or attitude information in n-frame with the help of external horizon or position information[3]. In SCNS/RSINS integrated navigation system, the accuracy of RSINS’s initial alignment can be improved. Recently, some SCNS/SINS integrated navigation technologies have been applied in aviation, marine and aerospace. In [4], the author studies the installation error of star sensor in a simple SCNS/SINS integrated model and the estimation method of IMU constant error by using the observations of star sensor. In [5], a reduced order model was studied through a SCNS/SINS integrated algorithm which took Mathematical Platform Misalignment Angle (MPMA) as measurement. However, in the SCNS/SINS integrated navigation system, the positioning accuracy of SCNS is largely affected by the external horizontal reference provided by SINS[6]. In order to solve this problem, a high-precision virtual horizontal reference determination algorithm based on data-fusion of star sensor and SINS is proposed in [7].

Typically, we utilize kalman filter to fuse SCNS/ RSINS integrated navigation system’s data. The design of the traditional filter is subjected to with filter-drivenfilter instabilities. Also, in order to implement a standard KF, a prior knowledge of the plant model is required to compute both the prediction of the state estimate and its Jabobian matrix. Often, the plant model is not completely known due to mismodeling, extreme nonlinearities, or the changes of system parameters from system’s wear and damage[8]. Consequently, the relatively new design need to be justified when used in the integrated system. We develop an adaptive state-estimation technique by using AIMMF algorithm to improve the performance of SCNS/RSINS integrated navigation system. The observation of SCNS/RSINS system come from AIMM structure in which the state-coupling function is augmented by the adaptive filter which captures the uncertainty dynamics. AIMMF is a parallel filtering algorithm with model matched, it is based on model switching configuration by adaptive filter[9].

The AIMM algorithm has been originally applied to target tracking, and recently extended to Global Positioning System (GPS) navigation[10], CNS and integrated navigation. A model probability evaluator calculates the current probability of the ship in each possible mode. This algorithm carries out a soft-switching between the various modes by adjusting the probability of each mode, which is used as a weighting in the combined-globestate estimation. IMMF will be used for fusing the data of the tightly-coupled SCNS/RSINS integrated navigation. Estimation accuracy and rapidity will be improved by using the proposed IMMF method over the conventional federated filter and EKF[10].

This paper is organized as follows: In Section 2, the coordinate frames used in this paper are introduced. In Section 3, the principles of SCNS and the fixing relations between SCNS and RSINS are presented. In Section 4, the algorithms based on the two different measurement equations are discussed as well as the proposed sensor fusion strategy. In Section 5, simulations and experiments are carried out. Finally, conclusions are given in section 6.

2 Reference coordinate frame

Coordinate frames used in this paper are defined as follows:

i-frame (the inertial frame): Earth-centered initially fixed orthogonal reference frame.

e-frame (the Earth frame): Earth-centered and earthfixed, orthogonal reference frame.

n-frame (the navigation frame): Orthogonal refe-rence frame aligned with East-North-Up geodetic axes.

b-frame(the vehicle’s body frame): Orthogonal reference frame aligned inertial measurement unit (vehicle) axes.

p-frame (the platform frame of RSINS): Orthogonal reference frame obtained by one successive transformation from body frame with a rotating angle.

s-frame (the star sensor frame): the body frame of SCNS.

The relationships between n-frame(on-xnynxn), p-frame (op-xpypxp) and b-frame (ob-xbybxb) are showed in Figure 1.is the angle velocity of b-frame relative to i-frame coordinatized in the b-frame,θ is axis tilt.

Fig.1 Relationship between the three coordinates

where η is the platform error angle.

3 Description of the general requirements

The SCNS/RSINS integrated navigation system is influenced greatly by initial information and inertial sensor errors. To solve this problem, it is important to find a reasonable combined-model and an optimization algorithm to calibrate those errors and compensate them.

3.1 Principle of SCNS

SCNS is based on star sensor technology as a high-precision attitude measuring device. It works as follows: regards stars as reference objects, treats the star field as work object and captures starlight by star sensor directly, then uses computers to calculate the guide-stars’centroid extraction, simulate and recognize the star map, and finally confirms the real-time pointing variation of the star sensor’s optical axis. SCNS can achieve a high-precision attitude in i-frame independently, and get position or attitude in n-frame by the aid of external horizon or position information. The working principle of SCNS is showed in Figure 2.

From Figure 2, we can see that SCNS has the capacity to get high-precision inertial-attitude without any prior information, also can get the position or attitude in n-frame with the help of prior external horizon or position reference. Finally we can obtain the position (latitudeφSCNSand longitudeλSCNS) or attitude (rollα, pitchβ and headingγ) in n-frame.

Fig.2 Principle of strapdown celestial navigation system

3.2 System calibration between RSINS and SCNS

RSINS and SCNS are installed on a common base independently. For SCNS’ positioning determination needs external horizontal reference provided by RSINS, so we should confirm the installation relation between this two systems at first. The installation error between RSINS and SCNS can be calibrated by auto-collimation theodolites or electronic gradienters, then the attitude transfer matrixcan be calculated. The way of calibration in outfield is shown in Figure 3. We assume the installation error θs(θs=(θsx,θsy,θsz)) is a small attitude error vector. The attitude matrixcan be calculated as follows:where, (θs×)is the cross-product antisymmetry matrix composed ofθscomponents.

Fig.3 Calibration of the installation error

4 Two parallel filters in SCNS/RSINS integrated navigation system

Suppose the installation error is calibrated and compensated. From the basic principle of SCNS, we know the advantages of SCNS: it can translate its data in i-frame to n-frame with other sensors’ horizon or position reference help. It means some errors of the external sensors, which cannot provide an absolutely accurate information, will introduce into SCNS. In traditional SCNS/RSINS integrated navigation system on shipboard, the external horizontal reference of SCNS is provided by RSINS as shown in Figure 4, so the attitude error of RSINS is introduced into SCNS. In order to improve the accuracy, a combined calibration method includes two parallel Kalman filters is designed for the tightly SCNS/ RSINS integrated navigation system. Kalman filter 1 is designed to reduce the influence of RSINS attitude error introduced into SCNS, and Kalman filter 2 is designed to improve the accuracy of SCNS/ RSINS integrated navigation system by fusing their outputs. The principle of combined calibration method is based on a tight SCNS/ RSINS model as shown in Figure 5.

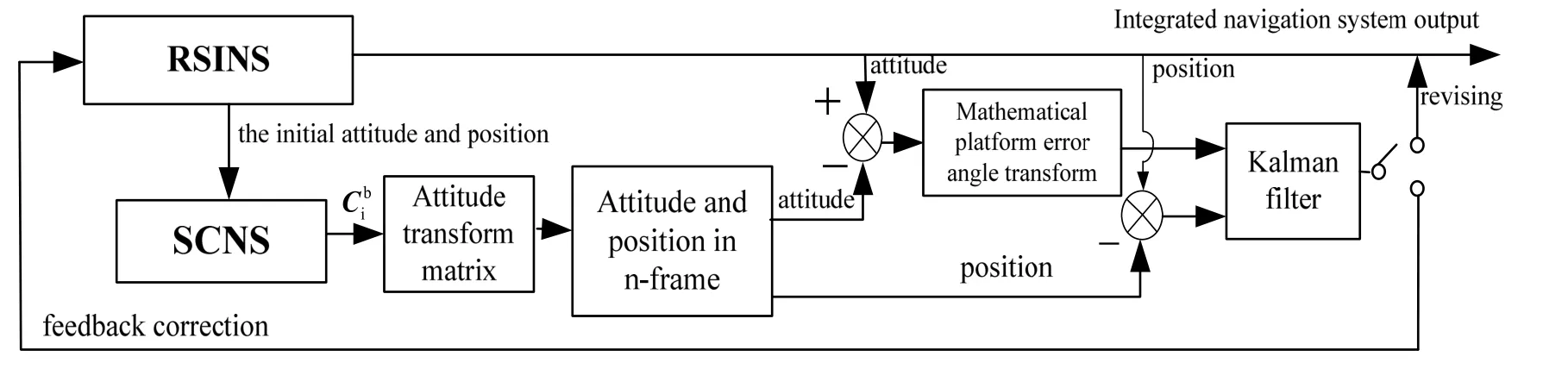
Fig.4 Principle of traditional SCNS/RSINS integrated navigation system

Fig.5 Principle of SCNS/RSINS tight combination model

4.1 Kalman filter 1 is based on quaternion algorithm

The gyroscope constant drift can be calibrated by fusing time-independent, high precision attitude information of SCNS. In i-frame, SCNS can get the attitude quaternionof vehicle by observing stars without any external information, while RSINS can calculate the vehicle's attitude quaternionfrom the outputs of gyroscopes. However,is much more precise thanso we consideras real-value, and treatas actual measuring value. The difference between them is defined as follows:

We suppose all the calculation of Kalman Filter 1 is in i-frame. And then the Kalman Filter model is defined as follows:

① State variables

Choose the RSINS quaternion error and gyro drift as states:

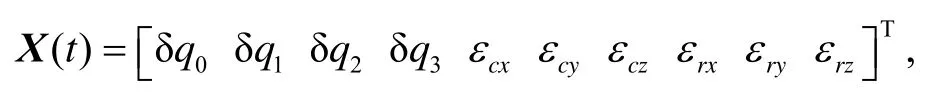
② State equations

1) Attitude quaternion error model:

RSINS transform quaternion update differential equation is:

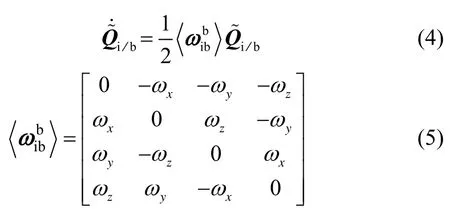
The differential equation of RSINS’s measurement quaternion equations are:

2) The gyroscope drift model:

Eq.(8) shows the relationship between attitude quaternion error and gyroscope’s angle rate. The gyroscope drift consists of two parts: constant drift and markov process. Its model can be given by:

So the state equations can be derived from Eq.(8) and (9):

where,

F1(t)is state translation matrix, G1(t)is observation noise matrix.

③ Measurement equations

where,H1(t)=[I4×404×6],V1(t)is measurement noise.

4.2 Kalman filter 2 is based on federal EKF

Kalman Filter 2 has two functions: one is to estimate the gyroscope drift, accelerometer bias and the integrated system’s errors, the other is to correct RSINS’s outputs. Its fundamental principle is summarized as follows: treat RSINS’ error equations as state equations, and regard the position and heading differences of SCNS and RSINS as measurement, then use Kalman Filter algorithm to fuse this two system’s outputs.

The SCNS/RSINS combined calibration model is summarized as follows: the RSINS and Inertial Measurement Unit’s errors are chose to be state variables, the difference of position and heading between SCNSand RSINS are chose to be measurement, then use Kalman Filter algorithm to estimate all errors, and then improve the RSINS’s accuracy by error compensation.

The combined calibration model of SCNS/RSINS integrated system is as follows:

① State variables

Take X=[δvx,δvy,δvz,δφ,δλ,δh ,α,β,γ,εx,εy,εz,as state variable, （α,β,γ） is platform error angle, (δφ,δλ) is position error, (δvx,δvy,δvz) is velocity error, (εx,εy,εz) is gyroscope constant drift, (Δbx,Δby,Δbz) is accelerometer zero bias.

② State equations

RSINS’s errors equations are used as the state equations in SCNS/RSINS integrated navigation system:

Where: F is the state transition matrix, the component of Fis given by

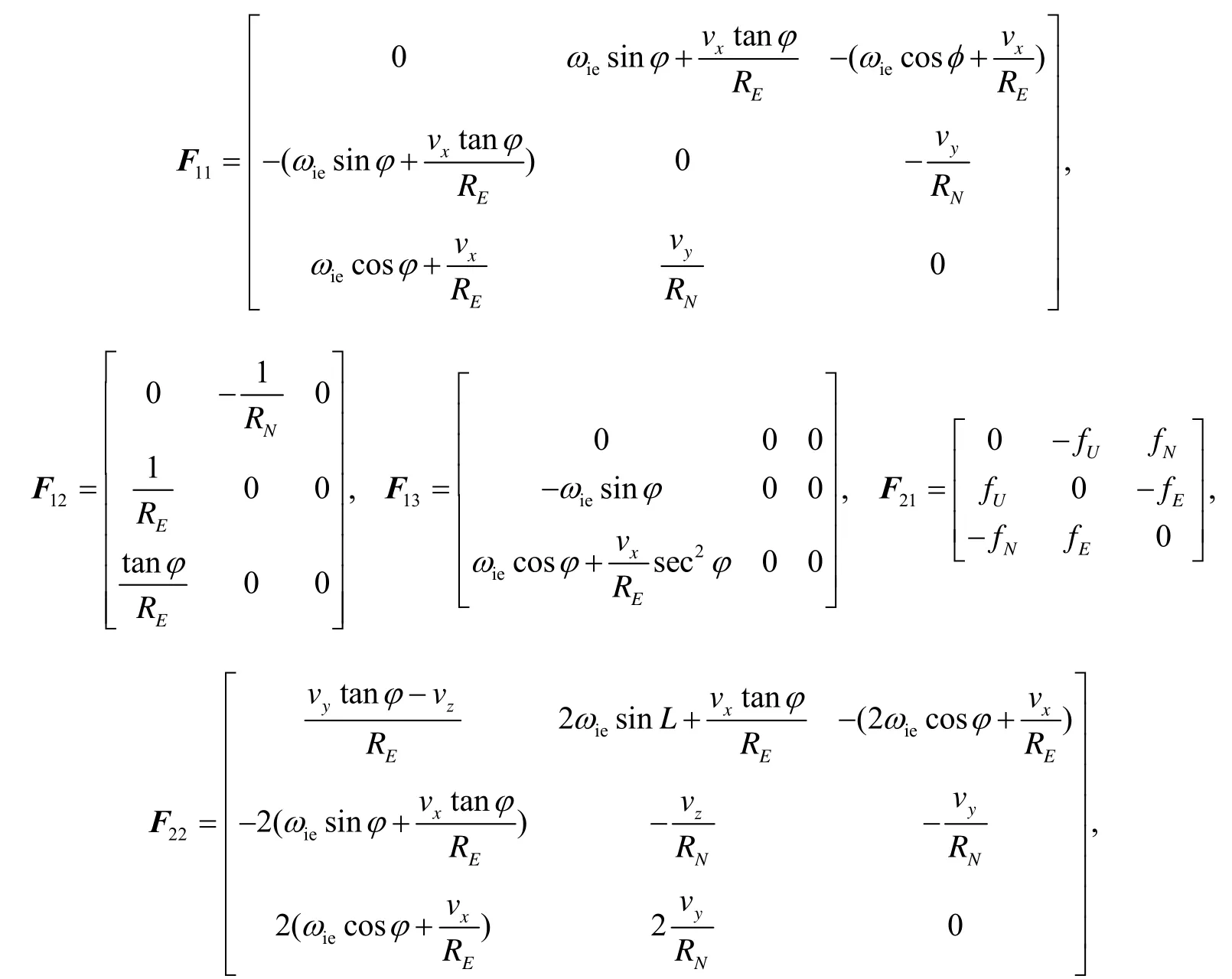
G is the noise distribution matrix,

W=[nεxnεynεzn∇xn∇yn∇z]Tis the process white noise, (nεx,nεy,nεz,n∇x,n∇y,n∇z) is the variance of gyroscope drift and accelerometer zero bias.

③ Measurement equations

We treat the position and heading differences between RSINS and SCNS as measurement, so the system measurement equations are written as follows:

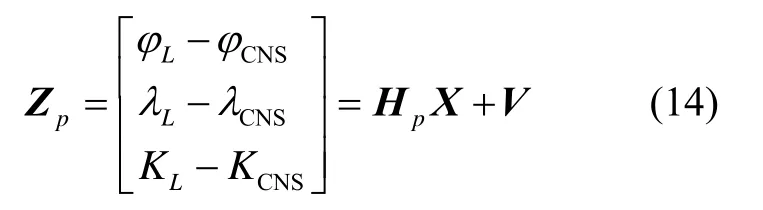
where,(φL,λL) is RSINS’ position, and KLis its’heading, while (φSCNS,λSCNS)is SCNS’ position and KSCNSis its’ heading;is observation matrix, Vis a 3-demensional measurement white noise matrix.

4.3 AIMMF algorithm

AIMMF is a filtering method where, the system state estimate is the proper combination of N estimates computed in accordance with N selected system error models. The various state models can be formed of different dimensions and driven by process noise of different statistics. The AIMMF algorithm performs almost like the exact Bayesian filter, but requires a far lower computational power. This is the reason why an AIMMF algorithm is preferred for practical applications. The algorithm consists of running a filter for each model, a model probability evaluator, and an estimate and covariance combination at the output of the filters. Each filter uses a mixed estimate at the beginning of each cycle, which is determined by the probabilities of switching between models, is the most important feature of AIMMF.

① Model mixing

Model mixing is an initialization of each filter. In this step, the same “current” model sequences are merged to obtain a weighting summation.

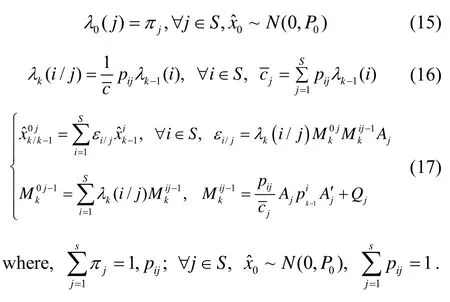
② Parallel filtering

Each filter performs kalman filtering when z(k) is received. For a model mi(k), the outputs are the state estimate , the covariance matrix Pi(k/k), thecovariance matrix Si(k) and the innovation vector υi(k).

③ The likelihood function for the filter with the model is:

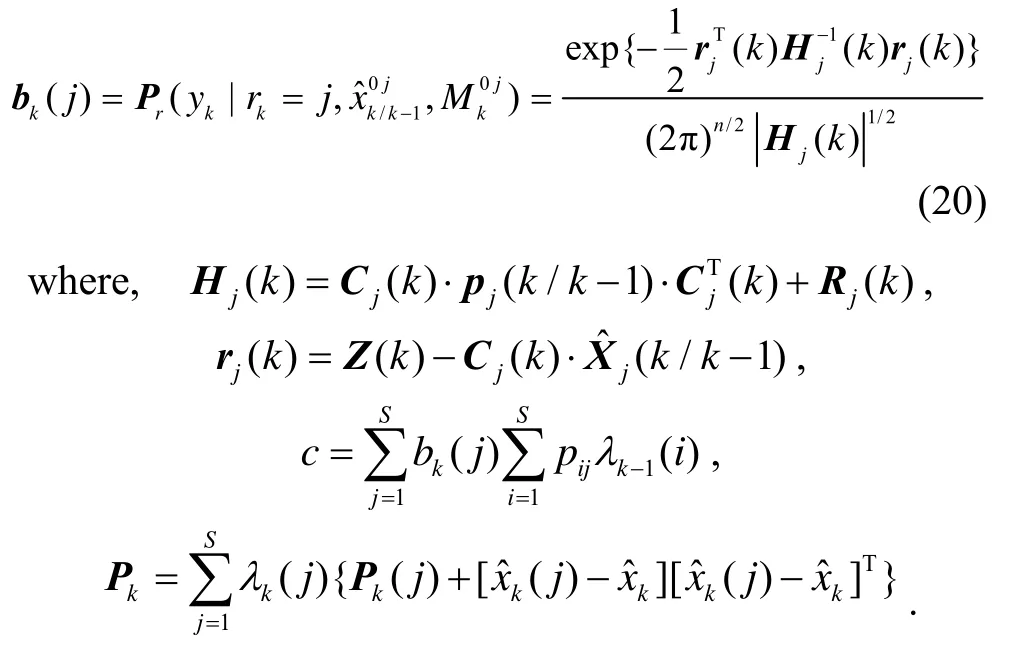
④ Estimation and covariance combination

The model-individual estimates and covariance are combined to an overall state and covariance:

In AIMMF algorithm, in order to detect the change of sensors errors model statistics, assuming two models, and the chosen model transition probability matrix is:

5 Simulations

To verify and estimate the performance of AIMMF algorithm for SCNS/RSINS integrated initial alignment, simulations are performed in this section. Suppose the initial parameters, raw measurement errors of star sensor and inertial sensor are given as follows:

① The initial latitude and longitude: φ0=39.1813, λ0=117.1140;

② The initial velocity components: vx=0, vy=0;

③ The acceleration due to the gravity: g0=9.8014 m/s2;

④ The initial misalignment angles: φx0=-4°, φy0=3°, φz0= -10°;

⑤ The gyro constant drifts of Rotation SINS: εx0= 0.0056 °/h, εy0=-0.0061°/h, εz0=0.0032°/h;

⑥ The gyro random noises of Rotation SINS: εrx= εry= 0.003 °/h, εrz=0.002°/h;

⑦ The accelerometer constant biases of Rotation SINS: ΔAx0= 10×10-5g, ΔAy0=-4×10-5g, ΔAz0=11×10-5g;

⑧ The accelerometer random noises of Rotation SINS: ΔArx=ΔAry=ΔArz=5×10-6g;

⑨ The bias error of Strapdown Celestial Navigation System: ΔSc0=1″;

⑩ The random noise of Strapdown Celestial Navigation System: ΔScr=3″;

⑪ The sample interval of the inertial sensor is 0.025 s,and the update period of Strapdown Celestial Navigation System is 1 s in the simulation.

Fig.6 Simulation of accelerometer bias and azimuth gyro drift based on extended Kalman filter

Fig.7 Simulation of accelerometer bias and azimuth gyro drift based on interacting multiple model filter

Fig.8 Comparison on alignment results of IMMF and EKF in static condition

Under the above simulation conditions, we apply the proposed AIMMF and EKF to estimate the errors of SCNS/RSINS integrated navigation system. Firstly, we assume that the alignment time lasts 30 min and the estimation time of Azimuth Gyro drift lasts 10 hr, then perform the alignment and calibration. We find the AIMMF’s accelerometer bias estimation is almost the same as EKF under static conditions. Through analysis of Figure 6 and Figure 7, we can find the accelerometer bias’s estimation accuracy of AIMMF has no obviousdifference from EKF, while the convergence time only has slight difference, EKF takes almost 7 hr and AIMMF takes about 4 hr to converges to the actual Azimuth Gyro drift, the convergence time of estimating gyro drift of AIMMF’s is 40% shorter than EKF and the estimation accuracy of Azimuth Gyro drift of AIMMF is better than EKF. Similarly, Figure 8 indicates the convergence time of AIMMF horizon attitude error is almost equal to EKF, and the azimuth attitude error converges to the zero line after less than 5 hr in AIMMF while the EKF hasn’t become stabilized yet after about 7 hr.

6 Conclusions

The performance of the parallel filters depends on the measurement system, whose two subsystems can be used. We analyze AIMMF technique and implement the application of AIMMF to the integrated alignment of SCNS/RSINS to enhance its adaption. Simulations are carried out with different parameter settings and platform rotation conditions, and the following conclusions can be drawn:

1) With single sensor, the alignment performance will not be improved by the filtering of the system, with complementary SCNS to RSINS, the alignment performance will be improved greatly through AIMMF algorithm.

2) Under static conditions, the difference is not significant in misalignment angle estimation accuracy between AIMMF and EKF, but the convergence time of the azimuth gyroscope drift can be shortened at least 40% in AIMMF algorithm.

As a whole, a reasonable measurement equation and an optimized error model will provide improvement in estimation accuracy and rapid capacity.

Reference:

[1] Rogers R M. Applied mathematics in integrated navigation systems[M]. 3rd Ed. AIAA: Reston, VA, USA, 2007.

[2] Liu X, Xu X, Liu Y. A method for SINS alignment with large initial misalignment angles based on Kalman filter with parameters resetting[J]. Math. Probl. Eng., 2014, 2014: 346291.

[3] 周凌峰, 赵小明, 赵帅, 等. 基于递推最小二乘估计的CNS/INS组合导航系统初始对准[J]. 中国惯性技术学报, 2015, 23(3): 281-286. Zhou Ling-feng, Zhao Xiao-ming, Zhao Shuai, et al. Initial alignment of CNS/INS integrated navigation system based on recursive least square method[J]. Journal of Chinese Inertial Technology, 2015, 23(3): 281-286.

[4] Ning Xiao-lin, Wang Long-hua, Wu Wei-ren, et al. A celestial assisted INS initialization method for lunar explorers[J]. Sensors, 2011, 11: 6991-7003.

[5] Thein M L, Quinn D A, Folta D C. Celestial navigation: Lunar surface navigation [C]//Proceedings of the 2008 AIAA/AAS Astrodynamics Specialist Congress and Exposition. Honolulu, USA, 2008: 1-19.

[6] Qu Qiang, Liu Jian-ye, Xiong Zhi. Inertial/Celestial attitude integrated algorithm based on additive quaternion[J]. Journal of Chinese Inertial Technology, 2013, 31(2): 397-403.

[7] Fei Yu , Lv Chong-yang, Dong Qian-hui. A novel robust H∞filter based on Krein space theory in the SINS/CNS attitude reference system[J]. Sensors, 2016, 16: 396.

[8] Feng J, Yu F, Zhang P, et al. On initial alignment of large azimuth misalignment for SINS on the static base in Krein space[C]//Proceedings of the IEEE 2012 10th World Congress on Intelligent Control and Automation. Beijing, China, 2012: 1964-1968.

[9] Gao S, Zhong Y, Zhang X, et al. Multi-sensor optimal data fusion for INS/GPS/SAR integrated navigation system[J]. Aerosp. Sci. Technol., 2009, 13: 232-237.

[10] Tseng Chien-Hao, Chang Chih-Wen, Dah-Jing Jwo. Fuzzy adaptive interacting multiple model nonlinear filter for integrated navigation sensor fusion[J]. Sensors, 2011, 11: 2090-2111.

[11] Gao Wei, Zhang Ya, Wang Jian-guo. A strapdown interial navigation system/Beidou/Doppler velocity log integrated navigation algorithm based on a cubature Kalman filter[J]. Sensors, 2014, 14: 1511-1527.

[12] Cho Taehwan, Lee Changho, Choi Sangbang. Multisensor fusion with interacting multiple model filter for improved aircraft position accuracy[J]. Sensors, 2013, 13: 4122-4137.

基于自适应交互多模滤波的SCNS/RSINS紧组合对准方法

周凌峰1,3，董燕琴2，赵汪洋3，赵小明1,3，屈原津3，侯志宁3
（1. 哈尔滨工程大学 自动化学院，哈尔滨 150001；2. 火箭军装备研究院，北京 100092；3. 天津航海仪器研究所，天津 300131）

为了提高船用单轴旋转捷联惯性导航系统（RSINS）初始对准的精度和快速性，针对传统的EKF滤波线性化误差和单传感器精度不高的问题，设计了一种基于自适应交互多模(AIMM)算法的SCNS/RSINS紧组合对准方法。该算法将自适应滤波器与交互多模型相结合，利用了两个合理构建状态模型和量测模型的平行滤波来实现对实际模态的覆盖：滤波1应用姿态四元数算法建立了状态方程的模型，量测量为RSINS与SCNS之间的姿态四元数误差；滤波2的根据SCNS/RSINS的误差特性构建了状态方程模型，量测量为RSINS与SCNS位置和航向误差，然后应用自适应IMM算法将两个平行滤波的估计值进行数据融合。在某种程度上，因状态噪声和量测噪声的不确定性，EKF的性能会被降低，而通过模型转换机制，IMM可用于选择一个合理的模型自动计算器来自适应地调整对准过程中噪声的协方差矩阵，因此该算法可以有效地解决SCNS/RSINS组合导航系统的初始对准问题。仿真结果表明：与EKF算法相比，基于自适应IMM算法的SCNS/RSINS组合对准方法的估计精度和对准快速能力都得到了改善，其中对方位陀螺漂移的估计时间缩短了至少40%。

SCNS/RSINS组合导航系统；扩展卡尔曼滤波；自适应交互多模滤波算法

U666.1

：A

2016-05-21；

：2016-07-07

国家重大科学仪器设备开发专项（2013YQ310799）

周凌峰（1981—），女，博士研究生，主要从事导航、组合导航与系统控制研究。E-mail: zhzhwy@163.com

1005-6734(2016)04-0464-09

10.13695/j.cnki.12-1222/o3.2016.04.009