膨胀环受力历史对应力应变关系的影响*

郭昭亮,范 诚,刘明涛,汤铁钢,刘仓理

(中国工程物理研究院流体物理研究所，四川 绵阳 621999)

膨胀环受力历史对应力应变关系的影响*

郭昭亮,范 诚,刘明涛,汤铁钢,刘仓理

(中国工程物理研究院流体物理研究所，四川 绵阳 621999)

利用两类实验装置开展了无氧铜TU1膨胀环实验研究，发现：电磁膨胀环在加载阶段，样品受体力作用，满足均匀变形的假定；而爆炸膨胀环在加载阶段，样品内壁受面力冲击作用，不满足均匀变形的假定。针对这个差异，发展了一种考虑冲击阶段变形不均匀性的新方法，利用回收样品几何变形，将冲击阶段试样环内轴向塑性应变、径向塑性应变纳入等效塑性应变的计算中，通过修正后的方法更准确地获得了材料的应力应变关系。

固体力学；应力应变关系；高应变率；膨胀环；无氧铜

材料及结构在高应变率下的变形与破坏行为，一直是学术界与工程界关注的焦点。圆环作为准一维的结构，因其简单的受力状态在研究材料动力学性能方面得到许多关注。实现圆环自由膨胀的实验手段主要有爆炸膨胀环实验装置及电磁膨胀环实验装置，这两类装置各有特点[1-2]。膨胀环的理论基础，依赖于径向速度历史的测量，随着激光测速技术的发展，膨胀环技术进一步得到完善[3-4]。H.Zhang等[5-8]、S.A.Morals等[9]利用电磁膨胀环实验技术平台，结合VISAR测速、高速相机等实时观测技术，系统地研究了Al 6061-O膨胀环、柱壳在高应变率下的膨胀断裂及碎裂规律，以及表面镀膜对材料拉伸断裂性能的影响。汤铁钢等[10]改变了传统的两点起爆式爆炸膨胀环，设计了中心线起爆加载下的爆炸膨胀环实验技术，增加了加载的稳定性，使它更好地应用于材料的动态力学性能研究。此外，M.Z.Liang等[11]、郑宇轩等[12]在霍普金森杆上开展了膨胀环实验技术的探索，然而相比于传统的膨胀环加载技术，这些尝试还有待进一步完善。

爆炸膨胀环实验中，试样内壁首先受面力冲击，将依次历经冲击阶段、自由膨胀阶段以及破坏阶段；而电磁膨胀环实验中，样品仅在体力作用下运动。加载阶段的受力历史差异对后期的膨胀断裂行为的影响，一直没有得到足够的重视。目前，关注的重点是自由膨胀阶段的数据[13]，并通过外壁速度历史反演出应力应变关系。虽然在自由膨胀阶段试样环仅受环向拉应力作用，然而材料经历前期冲击阶段的作用后，是否对材料的应力应变关系产生了不可忽略的影响，目前还尚未明确。

本文中，开展相同试样材料及几何结构的无氧铜(TU1)电磁膨胀环、爆炸膨胀环实验研究。发现在两类实验状态下，由于样品前期的受力历史的不同，将会导致采用相同处理方法获取的应力应变关系出现显著的差异。针对这个差异，发展一种考虑冲击阶段的变形不均匀性的新方法，利用回收破片的几何变形，将冲击阶段试样环中轴向塑性应变、径向塑性应变纳入等效塑性应变的计算中，可以获得爆炸膨胀环更真实的应力应变关系。

1 膨胀环受力历史分析

图1 电磁膨胀环截面变形Fig.1 Cross section shape of electromagnetic expanding ring

电磁加载及爆炸加载下的圆环膨胀断裂过程，可分为3个阶段：(1)加载阶段，膨胀环在外力作用下获得动能；(2)自由飞行阶段，爆炸加载下驱动器与环分离，电磁加载下加载电流截断，试样环在环向拉应力σθ作用下减速自由飞行；(3)失稳破坏阶段，当试样环膨胀到一定程度，局域损伤达到阈值，颈缩或裂纹萌生，导致随后的整体失稳破坏。本文中，关注的是材料的应力应变关系，因此只涉及膨胀环膨胀断裂的前两个阶段。

电磁膨胀环实验装置示意图见文献[14]。加载阶段，试样环在体力(电磁力，忽略电流的趋肤效应)作用下加速飞行，满足σr=σz=0的假定(σr为径向应力，σz为轴向应力)；当线圈中电流截断之后，试样环在环向应力σθ作用下减速飞行。由于试样环在加载阶段受体力作用，其横截面形状在不同阶段保持相似性，如图1所示。

自由飞行阶段试样环中，环向应力、环向应变、环向应变率分别为：

(1)

式中：ρ0为材料的初始密度，r0为试样初始外径，r为试样实时外径。

对于电磁加载下的试样环运动，前两个阶段中，均满足εr=εz=-εθ/2的假定。依据Mises屈服准则，在应力主轴坐标系中，等效应力、等效应变可写为：

(2)

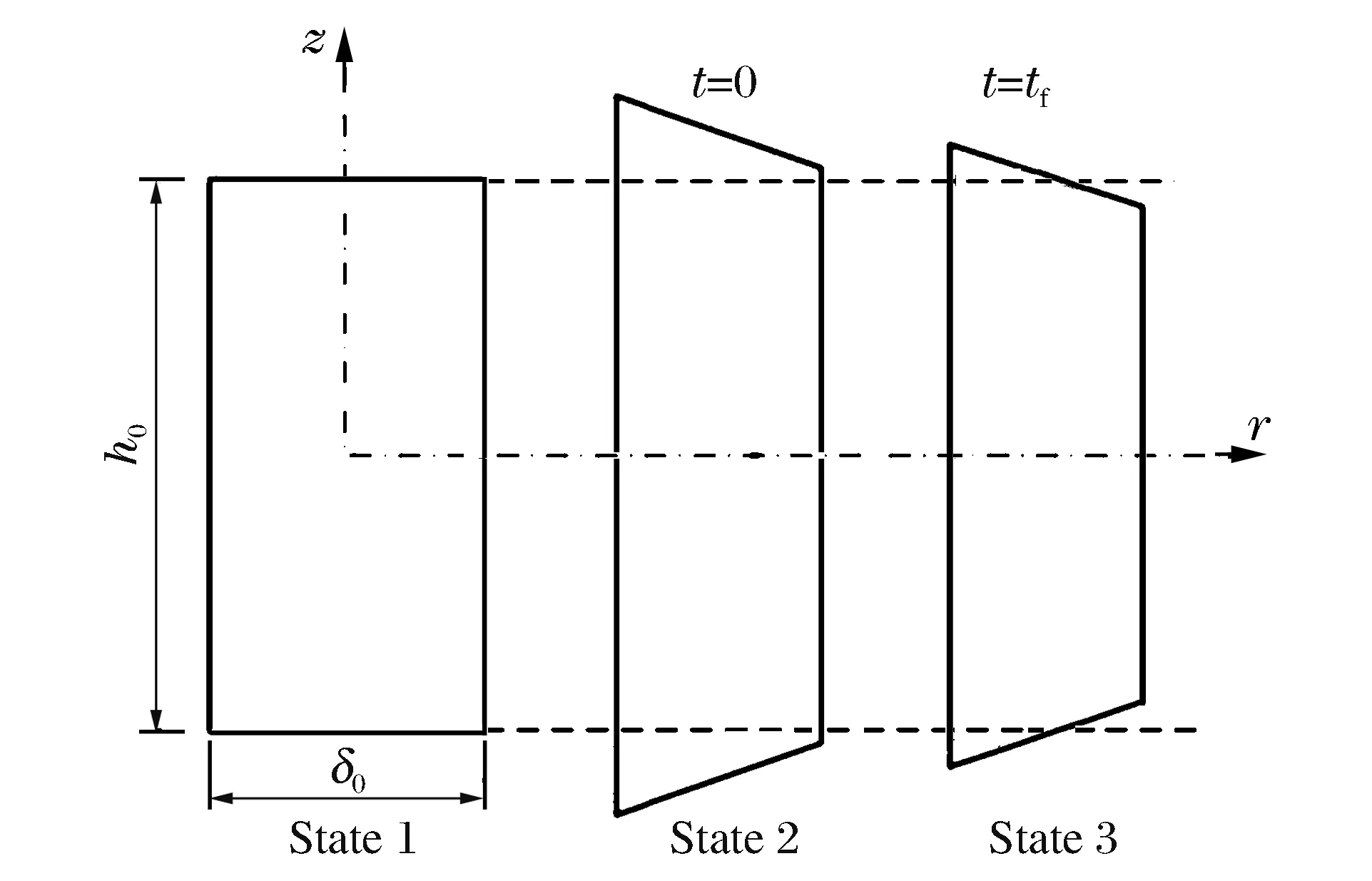
图2 爆炸膨胀环截面变形Fig.2 Cross section shape of explosive expanding ring

自由飞行阶段的膨胀环只存在环向应力，于是有等效应力、等效塑性应变：

σeff=σθ,εeff=εθ

(3)

与电磁膨胀环不同的是，爆炸膨胀环(实验装置见文献[10])在加载阶段，试样环内壁先受面力作用(驱动器冲击)，环向、轴向为复杂应力状态，冲击结束后膨胀环在驱动器加载下由初始状态1变形到状态2，试样径向位移很小，εθ≈0，且εr≠εz，因此εθ、εr、εz之间不存在定量的关联。在自由飞行阶段，膨胀环与驱动器脱开，在环向应力σθ作用下作减速运动，轴向、径向随着膨胀环的膨胀持续缩小，由状态2变形到状态3，如图2所示。

由以上关于膨胀环等效应力、等效塑性应变的推导可看出，爆炸膨胀环与电磁膨胀环的主要差异在于冲击阶段的受力历史。爆炸膨胀环在冲击阶段变形不均匀的原因来自于两个方面：内在原因，在于所选用的材料(无氧铜TU1)自身韧性较好，易发生较大变形；外在原因，在于加载为面冲击加载。在两种因素共同作用下，导致冲击阶段样品受冲击面获得比自由面更大的塑性变形，从而产生了应变的空间不均匀。而在爆炸膨胀环实验中，传统的获取应力应变关系的方法，仅仅考虑自由膨胀阶段的速度历史，忽略了冲击阶段的变形不均匀性影响，依据累积等效塑性应变的原则，这种处理将会低估材料的塑性变形，进而导致材料应力应变关系的不准确。本文中，针对无氧铜TU1环开展爆炸膨胀环、电磁膨胀环实验研究，主要阐述两类实验中不同加载历史对材料应力应变关系获取的影响。

2 实验及结果分析

选用无氧铜TU1作为试样材料，外径r0=21 mm，高度h0=2.02 mm，厚度δ0=1.02 mm。采用流体物理研究所的多普勒探针系统(Doppler pins system, DPS)，获得试样环的径向膨胀速度历史，如图3所示。并且，采用软回收装置获得了加载后的样品，如图4所示。

图3 膨胀环的径向速度Fig.3 Expanding velocities of expanding rings

图4 膨胀环回收样品Fig.4 Shaped rings collected from expanding ring experiments

表1 膨胀环实验数据 Table 1 Experimental data of expanding rings

爆炸膨胀环实验中，冲击阶段沿着径向存在应力波的传播。从图3(b)中可以看出，大约2 μs之后应力趋于平衡，随后进入自由飞行阶段，环向没有应力波传播，只存在拉伸加载，直至局域颈缩出现。颈缩出现之后，样品环中以颈缩点为源出现沿着环向的卸载波传播，颈缩之后的数据已经不再适用于研究材料的本构关系，本文中所讨论的是颈缩之前的变形过程，所以采用自由膨胀阶段的速度，对于冲击阶段只考虑了冲击所带来的预变形。为了获得爆炸膨胀环在膨胀过程中径向与轴向的实时应变εr(t)及εz(t)，我们做了如下近似。

近似1：在冲击阶段结束后，εr(t)及εz(t)达到最大值εr,max(t)及εz,max(t)，并以此时刻作为时间基准点，随后试样进入自由飞行阶段，εr(t)及εz(t)线性减小至终态应变(即回收样品的测量应变)，由于在冲击阶段轴向应变沿厚度方向分布不均，为简化模型，可以取平均值进行估计。于是径向及轴向应变为：

(4)

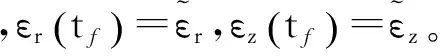
近似2：自由飞行阶段，试件均匀变形，体积不变。轴向塑性应变与径向塑性应变增量满足Δεr=Δεz=-εθ/2，于是有：

(5)

由式(4)～(5)，可得轴向应变、径向应变：

(6)

利用图3中无氧铜TU1膨胀环速度曲线，可拟合出爆炸膨胀环径向应变与轴向应变：

(7)

式中：t的单位为μs。

依据塑性应变增量关系，可得爆炸膨胀环膨胀过程中环向应变、径向应变、轴向应变及等效塑性应变，如图5所示。在无氧铜爆炸膨胀环实验中，等效塑性应变与环向应变之间的关系，不同于式(10)的简单状态，而是需要附加冲击阶段带来的塑性变形。对于电磁膨胀环实验而言，等效塑性应变与环向应变几乎重合。

将冲击阶段对材料变形的影响，纳入等效塑性应变的计算之中，可以获得爆炸膨胀环、电磁膨胀环自由飞行阶段环中的应力应变关系，如图6所示。

利用式(1)，可得自由飞行阶段爆炸膨胀环最大应变率为5 380 s-1，电磁膨胀环最大应变率分别为1 930、2 890、3 900 s-1，其中速度选择自由飞行阶段的最大速度。可以看出，在不考虑冲击阶段影响的时候，利用爆炸膨胀环数据获得的应力应变关系会低估等效塑性应变，与电磁膨胀环所得数据存在较大差异，这个差异影响对材料真实应力应变关系的判读。而利用累积等效塑性应变原则，采用考虑冲击阶段εr与εz影响之后的新方法，获得了更真实的爆炸膨胀环应力应变关系，且与电磁膨胀环所得数据落在同一区域，两者之间可以相互佐证。另外，从图6可以看出，随着应变率的增加，应力出现一定的硬化现象，这与无氧铜的材料动力学特征相符。

图5 爆炸膨胀环的环向应变、径向应变、轴向应变及等效塑性应变Fig.5 Explosive expanding ring’s hoop strain, axial strain, radial strain and effective strain

图6 膨胀环的应力应变关系Fig.6 Relationship between expanding ring’s flow stress and effective plastic strain

3 讨论与结论

电磁膨胀环、爆炸膨胀环两类实验装置在研究材料动态力学性能方面，已经得到较广泛的应用，然而加载历史对其结果的影响并未得到有效的讨论。本文中，针对采用电磁膨胀环、爆炸膨胀环两类实验装置开展的无氧铜膨胀环实验研究，通过理论及实验两方面尝试阐明膨胀环受力历史对应力应变关系的影响。得到以下初步结论。

(1)电磁膨胀环在加载阶段受体力作用，满足均匀变形的假定；爆炸膨胀环在加载阶段内壁受面力冲击作用，不满足均匀变形的假定，这个不同将导致应力应变关系获取方法的差异。

(2)针对爆炸膨胀环的复杂受力历史，发展了一种考虑冲击阶段的变形不均匀性的新方法，通过无氧铜回收样品的几何尺寸分析，将冲击阶段的轴向塑性应变、径向塑性应变纳入到等效塑性应变的计算之中。实验结果表明，考虑冲击阶段膨胀环轴向塑性应变、径向塑性应变后，可以更准确、更真实地得到材料的应力应变关系。

(3)电磁膨胀环实验装置、爆炸膨胀环实验装置，在材料应力应变关系的研究中已经成熟，原理上并不存在本质的差别，针对不同的材料选择合适的加载手段以及分析方法，均可获得合适的本构关系。

(4)研究材料高应变下的本构关系，需要明确样品的受力历史，尤其是对于受面载荷作用的样品，需要对回收样品进行尺寸变化的统计分析，用于获得准确的等效塑性应变；本文中塑性应变获取方法，是一种普适的方法，对于脆性材料与非金属材料同样适用。

感谢张振涛、金山、陈浩玉在实验中的贡献。

[1] 桂毓林.电磁加载下金属膨胀环的动态断裂与碎裂研究[D].绵阳：中国工程物理研究院，2007.

[2] 汤铁钢.一种新型爆炸膨胀环实验技术及其应用[D].绵阳：中国工程物理研究院，2010.

[3] Warners R H, Duffty T A, Karpp R R, et al. An improved technique for determining dynamic material properties using the expanding ring[C]∥Meyers M A, Muri L E. Shock waves and high-strain-rate phonomena in metals. US: Springer, 1981:23-36.

[4] Warnes R H, Karpp R R, Follansbee P S. The freely expanding ring test: A test to determine material strength at high strain rates[J]. Journal of Engineering Materials & Technology, 1985,108(4):583-590.

[5] Zhang H, Ravi-Chandar K. On the dynamics of necking and fragmentation-Ⅰ: Real-time and post-mortem observations in Al 6061-O[J]. International Journal of Fracture, 2006,142(3/4):183-217.

[6] Zhang H, Ravi-Chandar K. On the dynamics of necking and fragmentation-Ⅱ: Effect of material properties, geometrical constraints and absolute size[J]. International Journal of Fracture, 2008,150(1/2):3-36.

[7] Zhang H, Ravi-Chandar K. On the dynamics of localization and fragmentation-Ⅲ: Effect of cladding with a polymer[J]. International Journal of Fracture, 2009,155(2):101-118.

[8] Zhang H, Ravi-Chandar K. On the dynamics of localization and fragmentation-Ⅳ: Expansion of Al 6061-O tubes[J]. International Journal of Fracture, 2010,163(1/2):41-65.

[9] Morals S A, Albrecht A B, Zhang H, et al. On the dynamics of localization and fragmentation-Ⅴ: Response of polymer coated Al 6061-O tubes[J]. International Journal of Fracture, 2011,172(2):161-185..

[10] Tang Tiegang, Ren Guowu, Guo Zhaoliang, et al. An improved technique of expanding metal ring experiment under high explosive loading[J]. Review of Scientific Instruments, 2013,84(4):043908-6.

[11] Liang M Z, Li X Y, Qin J G, et al. Improved expanding ring technique for determining dynamic material properties[J]. Review of Scientific Instruments, 2013,84(6):065114-5.

[12] 郑宇轩,周风华,胡时胜.一种基于SHPB的冲击膨胀环实验技术[J].爆炸与冲击,2014,34(4):483-488. Zheng Yuxuan, Zhou Fenghua, Hu Shisheng. An SHPB based experimental technique for dynamic fragmentations of expanding rings[J]. Explosion and Shock Waves, 2014,34(4):483-488.

[13] 汤铁钢,桂毓林,李庆忠,等.爆炸膨胀环实验数据处理方法讨论[J].爆炸与冲击,2010,30(5):505-510. Tang Tiegang, Gui Yulin, Li Qingzhong, et al. A discussion of data processing techniques for expanding ring tests[J]. Explosion and Shock Waves, 2010,30(5):505-510.

[14] 桂毓林，孙承纬，李强，等.实现金属环动态拉伸的电磁加载技术研究[J].爆炸与冲击,2006,26(6):481-485. Gui Yulin, Sun Chengwei, Li Qiang, et al. Experimental studies on dynamic tension of metal ring by electromagnetic loading[J]. Explosion and Shock Waves, 2006,26(6):481-485.

(责任编辑 丁 峰)

Effect of loading history on stress-strain relationship of expanding ring

Guo Zhaoliang, Fan Cheng, Liu Mingtao, Tang Tiegang, Liu Cangli

(InstituteofFluidPhysics,ChinaAcademyofEngineeringPhysics,Mianyang621999,Sichuan,China)

Electromagnetic driving expanding ring experiment and explosive expanding ring experiment are two important means for obtaining dynamic tensile mechanical properties of materials. In this study, they were carried out to investigate the dynamic behaviors of oxygen-free copper (TU1) expanding rings. The results show that, during the loading stage, samples driven by electromagnetic force satisfy the assumption of the uniform deformation due to the body force whereas it is not the case with the explosive expanding ring because the sample is impacted by the surface force. With respect to this difference, a new method considering the deformation inhomogeneity was established, where the axial plastic strain and radial plastic strain during impact stage was included in the calculation of the equivalent plastic strain. Through the revised method a more accurate stress-strain relationship of TU1 was obtained.

solid mechanics; stress-strain relationship; high strain rate; expanding ring; oxygen-free high-conductivity copper

10.11883/1001-1455(2016)06-0819-06

2015-04-16； < class="emphasis_bold">修回日期：2015-09-14

2015-09-14

国家自然科学基金项目(11172279)

郭昭亮(1984— )，男，助理研究员,glogos@caep.cn。

O347.3 <国标学科代码：1301515 class="emphasis_bold"> 国标学科代码：1301515 文献标志码：A国标学科代码：1301515

A