弹体高速侵彻效率的实验和量纲分析*

宋梅利,李文彬,王晓鸣,冯 君,刘志林

(南京理工大学智能弹药技术国防重点学科实验室，江苏 南京 210094)

弹体高速侵彻效率的实验和量纲分析*

宋梅利,李文彬,王晓鸣,冯 君,刘志林

(南京理工大学智能弹药技术国防重点学科实验室，江苏 南京 210094)

为了研究高速侵彻时弹体撞击速度、材料强度等对质量侵蚀特性和侵彻效率的影响规律，开展了不同材料强度和长径比的弹体高速侵彻半无限厚素混凝土靶实验，弹体撞击速度为880～1 900 m/s，弹头形状为尖卵型(半径口径比为3)，口径为30 mm。由实验发现：弹体撞击速度对侵彻效率的影响呈抛物线分布，最大侵彻效率时的弹体特征撞击速度约1 400 m/s；高速侵彻时弹体的质量侵蚀主要发生在卵形头部，弹身及尾部损伤极少；速度超过特征撞击速度时，弹体侵蚀严重，甚至弯曲变形或解体；弹体强度提高至约2倍时，质量侵蚀率降低约80%。基于实验，利用量纲分析原则建立了量纲一侵彻效率和量纲一弹体撞击速度的函数关系式，可估算出最大侵彻效率对应的弹体撞靶速度，为高速侵彻效应模拟实验提供理论指导。

爆炸力学；侵彻效率；高速侵彻；混凝土靶；质量侵蚀；量纲分析

宋梅利等[1]在动能弹高速侵彻混凝土靶研究中，提出了侵彻效率的概念，它为侵彻深度与弹体撞击速度的比(η=H/v0)，该定义能较直观地反映获得最大侵彻效率时弹体的着靶运动条件。随着撞击速度的提高，弹体的侵蚀效应变得显著，过高的撞击压力使弹体结构破坏，导致弹道弯曲，侵彻深度随着撞击速度的增大反而会减小，侵彻效率存在极大值。

20世纪80年代，就有人关注高速动能对地武器的侵彻效能，R.W.Nelson[2]进行了钢弹头侵彻钢筋混凝土的实验，结果表明，撞击速度大于900 m/s时，弹体发生了严重侵蚀，达到1 200 m/s时，弹体变形严重并破碎，侵彻深度降低，侵彻效率接近峰值。M.J.Forrestal等[3-4]进行了一系列尖卵形弹对混凝土靶的侵彻实验，弹体口径12.7 mm，撞击速度400～1 700 m/s，发现当撞击速度为1 200 m/s时，弹体出现严重侵蚀，侵彻效率最大，速度继续增加后，弹体会断裂或从靶的侧边飞出，侵彻能力和效率降低。R.N.Davis等[5]通过实验发现，随着撞击速度的增大，侵彻体头部变形严重、头部钝化，侵彻深度降低，弹体对靶侵彻性能和侵彻效率降低。Z.C.Mu等[6]和X.W.Chen等[7]也在研究中发现，高速侵彻时由于弹体弯曲、断裂或质量磨损，侵彻深度和侵彻效率均存在极值。以上表明，弹体高速侵彻时存在侵彻效率极大值现象。

由于弹体对混凝土的侵彻是一个复杂的物理过程，影响侵彻效率的因素很多，很难通过单独的数学分析方法得出一个精确的解，利用量纲分析法[8]可以很好地对弹体侵彻效率进行分析，弥补这种不足。虽然对高速侵彻已有很多的研究，但仍有一些空白：撞击速度1 000～2 000 m/s、弹体口径大于25 mm弹体的侵彻实验数据较少，且未充分归纳和分析；对一定的弹靶系统，无法预估获得最大侵彻效率的弹体着靶条件。

本文中，为了获得弹体撞击速度、材料强度、长径比等对侵彻效率及其特征撞击速度的影响规律，开展不同材料强度、不同长径比的弹体侵彻半无限厚素混凝土靶的高速侵彻实验，获得撞击速度880～1 900 m/s时弹体非刚性破坏等高速侵彻典型现象及不同速度下侵彻深度、弹体响应等参数，并根据实验数据拟合得到量纲一侵彻效率和量纲一弹体撞击速度的函数关系式。

1 实 验

图1 实验现场布局图Fig.1 Experiment layout

在原型弹基础上进行了缩比，采用的缩比率为1∶8.33。为达到预期的高发射速度，采用次口径发射技术，图1为弹道炮发射平台的实验现场布局图。用高速摄影测量弹体速度和着靶姿态，同时拍摄弹体飞行和弹靶初始作用过程，采用HG202计时仪和金属网靶测量弹体着靶速度。为了顺利回收弹体，尽量选用厚度大的靶体，且靶体周围用沙袋或废弃靶标围挡。

弹体材料为30CrMnSiNi2A，为分析材料强度对弹体侵蚀效应的影响，选取材料原始状态和经过热处理状态，两种状态对应的材料强度分别为856和1 650 MPa。受火炮发射能力的限制，达到1 900 m/s的着靶速度时，弹体质量应不超过330 g，因此设计弹体长径比分别为3和4，弹头部形状为尖卵形，头部半径口径比为3，弹体实物如图2。图3为次口径发射装置，该装置能够承受膛内火药气体的高过载，保证结构不变形，同时与弹体在膛内合理配合，保证弹体在膛内受力均匀、不漏气、不划伤炮膛等，从而使弹体在炮膛内正常运动并达到理想的速度，出炮口后弹托很快分离且不影响弹体的正常飞行。实验前弹体参数见表1，其中m0为弹芯初始质量，l0为弹芯初始长度，d0为弹芯圆柱部分初始直径，σp为弹体材料抗拉强度，弹体长径比μ=l0/d0。

图2 弹体实物Fig.2 Projectiles

图3 发射装置实物Fig.3 Projectile assembly

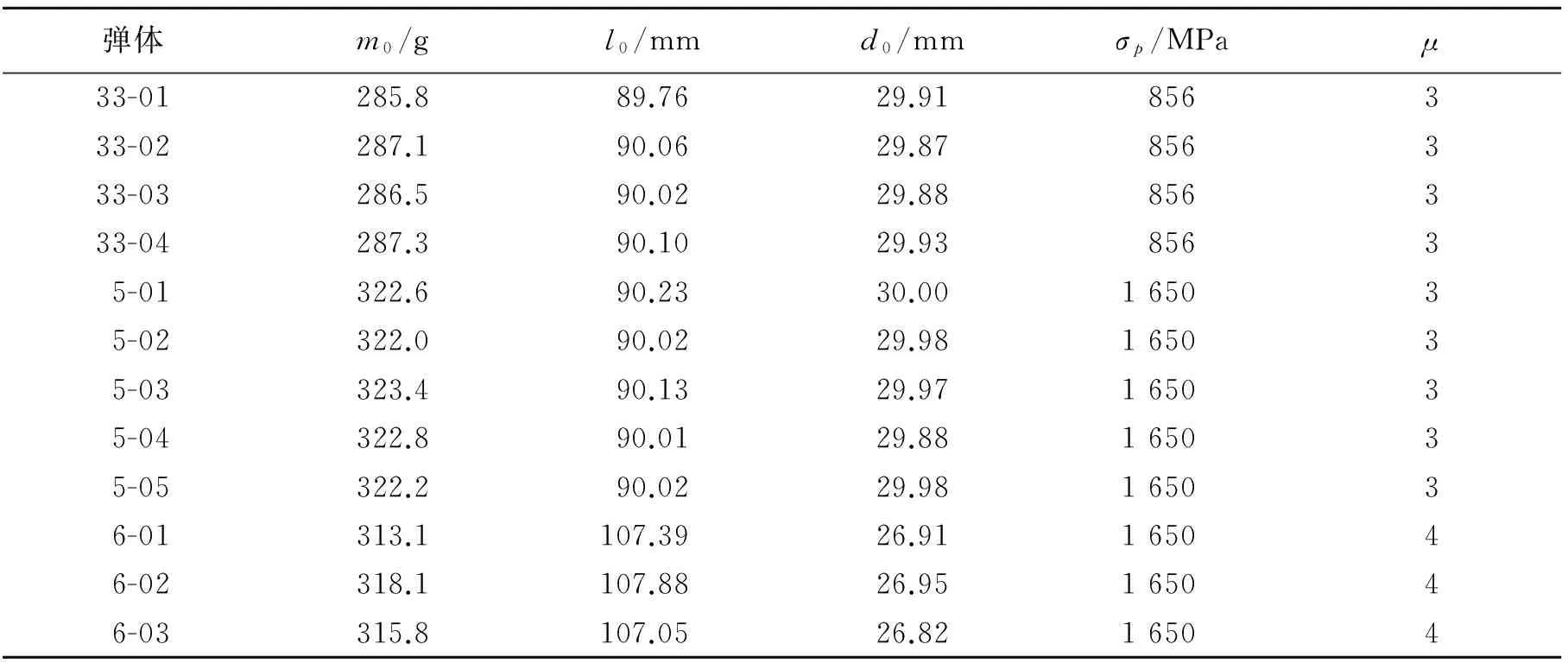
表1 实验前弹体参数Table 1 Parameters of projectiles before experiments

图4 混凝土靶体实物Fig.4 Concrete target

1.1 实验结果

弹体撞击速度范围为880～1 900 m/s，共取得有效数据12组，见表2。其中v0为弹体撞击速度，l为侵彻后弹芯长度，m为弹芯剩余质量，d为侵彻后弹芯圆柱部分直径，Δl/l为弹芯长度缩短率，Δm/m为弹芯质量损失率，α为偏航角，向左为“-”，向右为“+”，β为俯仰角，向下为“-”，向上为“+”，γ为侵彻弹道倾角，H为侵彻深度。

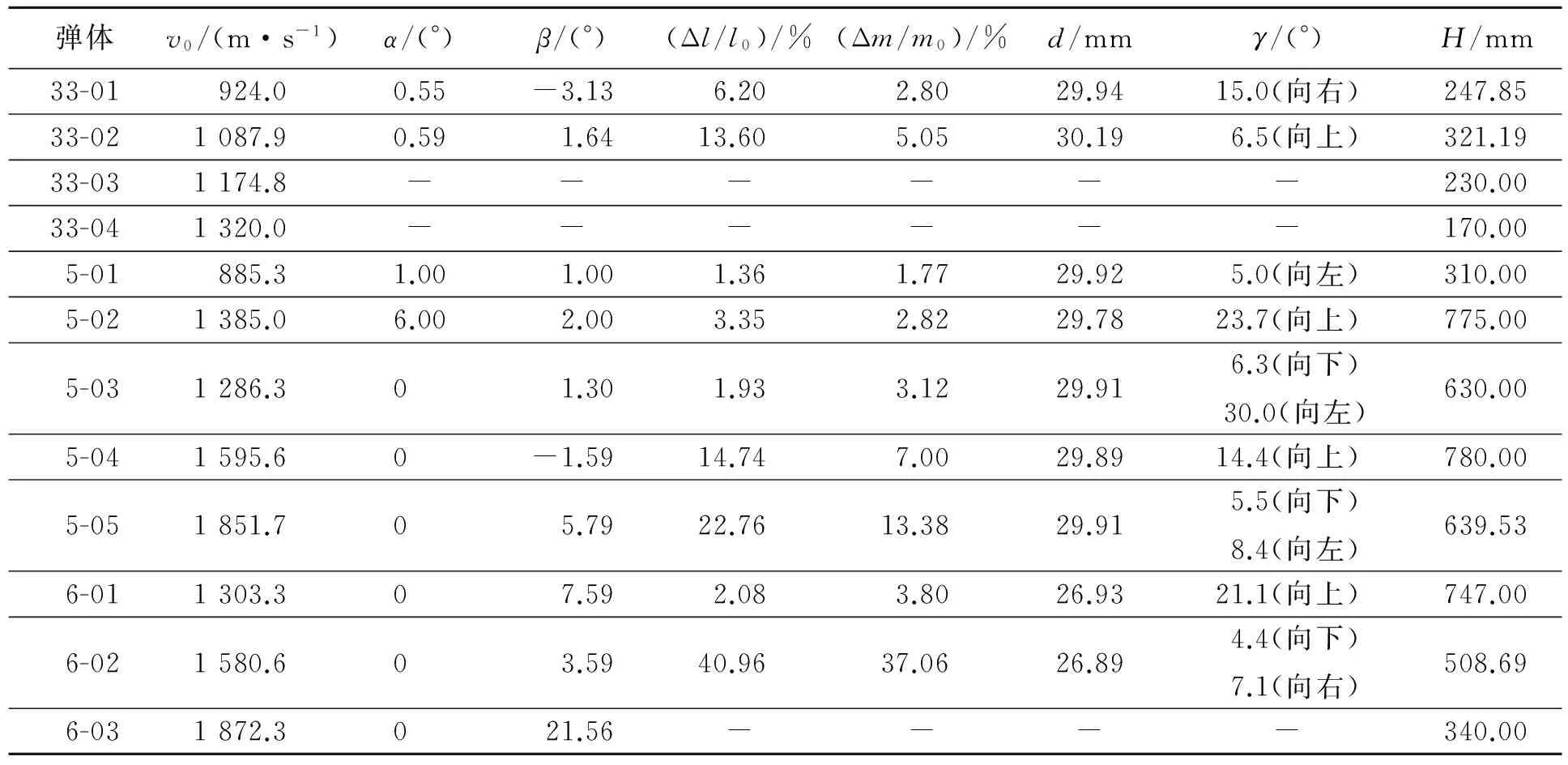
表2 实验后弹靶参数Table 2 Parameters of projectiles and targets after experiments

1.2 靶体破坏情况

图5 靶体破坏图Fig.5 Destroyed target

弹体以不同速度对靶的侵彻深度见表2，典型着靶面破坏情况见图5。可以看出，所有靶体表面在弹着点周围形成漏斗坑，靶板表面产生以弹着点为中心的径向裂纹。大部分靶体中紧随漏斗坑的是圆柱形隧道，隧道孔径大约与弹径相同或比弹径大10%以内，其中3发高速度弹体33-03、33-04、6-03由于撞击压力大，弹体强度不足使它撞击靶时弯曲变形或断裂，导致弹体很快失去侵彻能力，在靶表面只形成漏斗坑，没有形成有效的侵彻。表2数据显示，弹体着靶角α或β大于5°时，弹道倾角均较大，说明弹体运动姿态对弹道稳定性起重要作用；速度高于1 350 m/s时，即使着靶角不大(小于2°)，弹道倾斜也较严重，原因是速度高时，弹靶撞击压力大使弹体塑性变形或热软化，不对称头部侵蚀使弹体受力不均匀而导致弹道偏斜。

图6～7分别为两种强度弹体侵彻深度、侵彻效率随撞击速度的变化曲线，对于相同的弹体结构，当弹体材料强度由856 MPa增加到1 650 MPa时，即弹体强度提高至约2倍时，弹体的侵彻深度增加143%，侵彻效率增大89%，侵彻能力大大提高。图6显示，低强度弹体最大侵彻深度时弹体撞击速度约为1 080 m/s，而高强度弹体的撞击速度约为1 450 m/s。图7显示，低强度弹体最大侵彻效率对应的弹体特征撞击速度vmax约为1 050 m/s，而高强度弹体的vmax约为1 400 m/s。可以看出，随着v0的增大，侵彻效率先增大后减少，当v0接近vmax时，侵彻效率达到极值，此时侵彻深度虽然还未达到最大值，但已接近极值；之后，随着v0的增大，H会有所增加，但增加幅度较小。实验结果表明，对这两种材料强度的弹体，最大侵彻效率对应的vmax分别为1 050和1 400 m/s，v0再提高5%左右时，H达到极值。

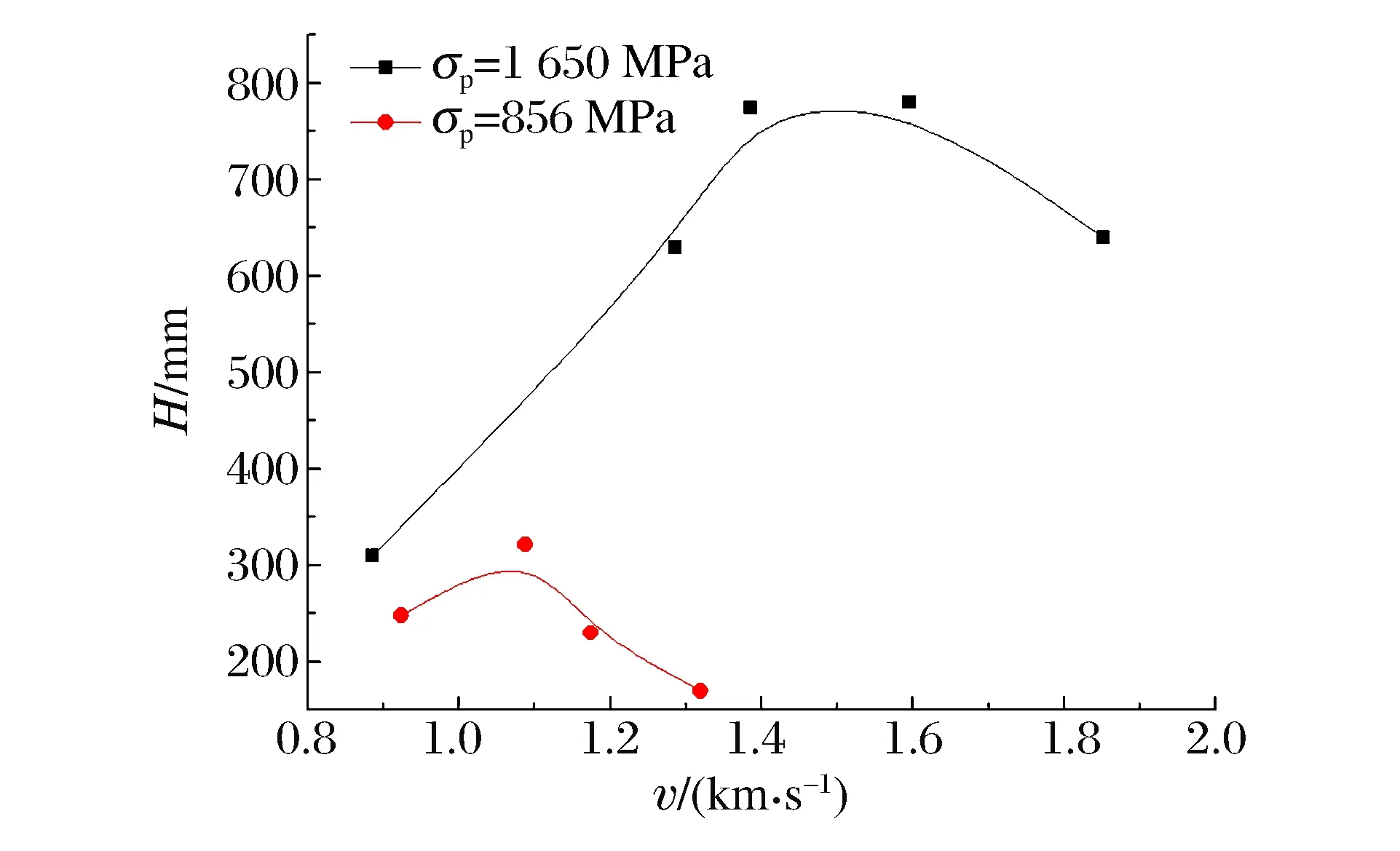
图6 侵彻深度随撞击速度的变化Fig.6 Variation of penetration depth with impact velocity

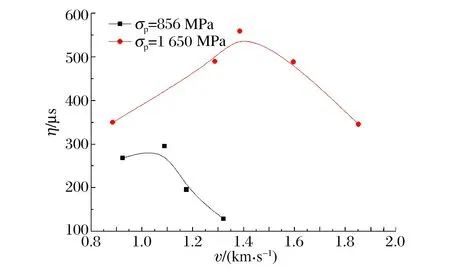
图7 侵彻效率随撞击速度的变化Fig.7 Variation of penetration efficiency with impact velocity

1.3 弹体破坏情况

实验后弹体参数见表2，图8为不同撞击速度的回收弹体。可以看出，随着撞击速度的增大，弹体质量侵蚀严重甚至弯曲断裂。质量侵蚀包括弹头部和圆柱部分的质量损失。表2和图8表明，弹体结构解体前，质量侵蚀主要集中在弹体头部，虽然侵彻过程中弹体圆柱部分会受到靶体的摩擦力，但圆柱部分的长度和直径几乎没有减少。部分弹体直径略有增大，主要原因是，侵彻过程产生的高温使混凝土粉末与弹体金属熔接在一起，而使直径略增。由滑动摩擦引起的弹体圆柱部分的质量损失，远少于由高温和高压流动侵蚀引起的卵形头部质量侵蚀，因此弹体质量侵蚀主要发生在卵形头部。此现象进一步验证了文献[9]的结论。表2还显示，当弹体材料强度从856 MPa提高到1 650 MPa时，即弹体强度提高至约2倍时，质量侵蚀率降低约80%。弹体长径比由3增大到4时，对于相同的弹体撞击高速(大于1 500 m/s)，长径比越大，弹体变形及破坏越严重，侵彻能力越差。

图8 回收弹体Fig.8 Projectiles after experiments

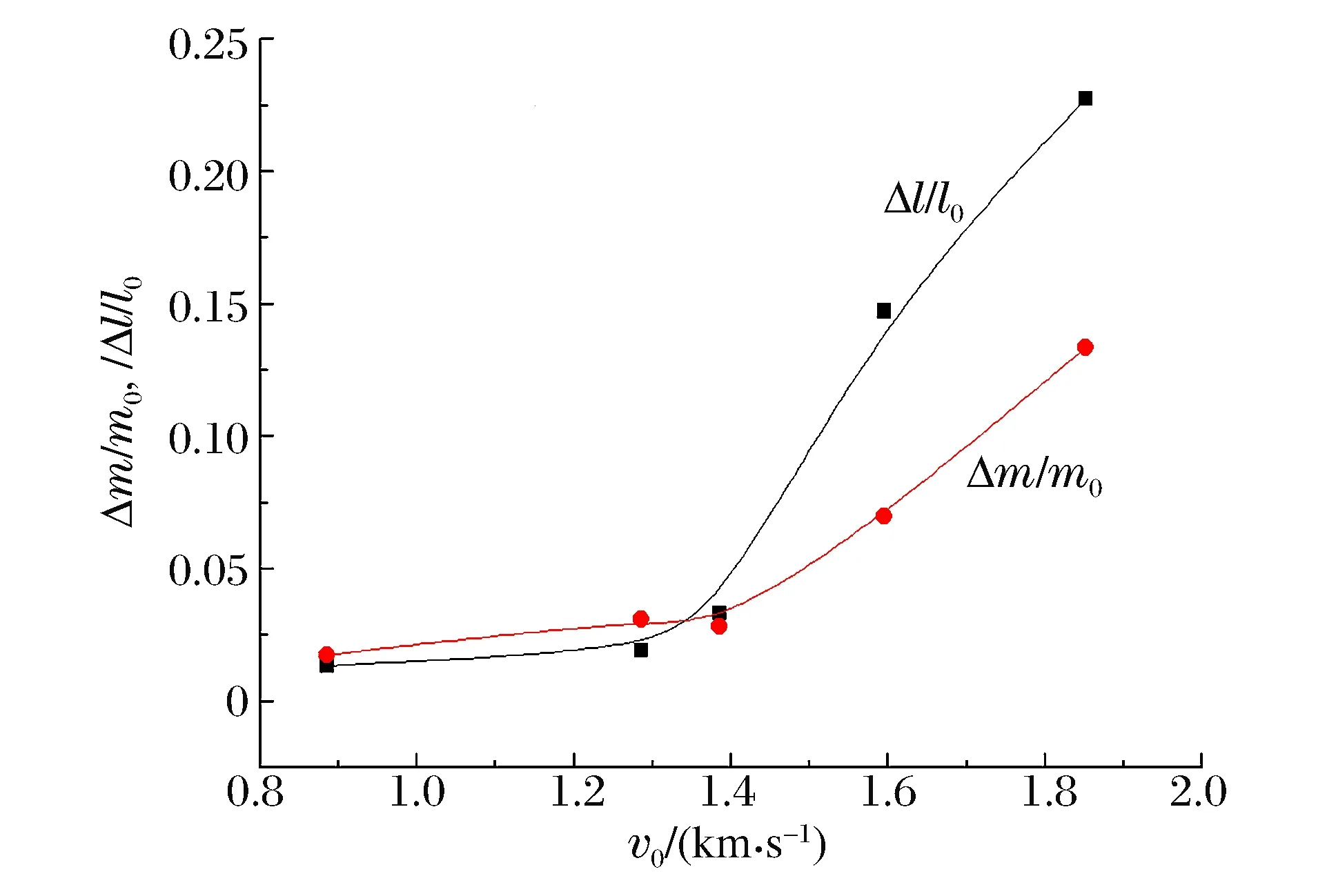
图9 质量损失率和长度缩短率随撞击速度的变化Fig.9 Variation of mass loss and length shortening with impact velocity

图9为弹体质量损失率Δm/m0和长度缩短率Δl/l0随弹体速度的变化规律，速度小于特征撞击速度vmax(约1 400 m/s)时，Δm/m0和Δl/l0随弹体速度的增大缓慢线性增长，质量损失率缓慢增加，且损失率小于5%，侵彻深度和效率随着撞击速度的增大而增加。速度达到vmax后，弹体动能产生的高撞击压力远超于弹体材料强度，高速撞击和强烈摩擦使弹头部软化，头部侵蚀严重，弹体甚至弯曲或断裂，增大了弹体的侵彻阻力，使侵彻深度和效率出现极大值。弹体沿轴向侵彻的过程中，弹头部受到混凝土硬骨料的切削作用，头部材料不断被移走，质量损失严重；同时，弹头部的软化和大塑性变形使弹体长度迅速减少，弹体质量损失也不再按原来的趋势缓慢增加，而是出现一个阶跃。

侵彻后的弹体和靶体显示，随着弹体撞击速度的提高，弹体不对称侵蚀和磨蚀非常严重，混凝土材料的非均匀性和各向异性使弹体的非均匀受力更明显，加之速度较高时弹体着靶姿态不正，导致弹体在靶体中运动偏斜，随着速度的增大侵彻弹道偏转角也随之增大。

2 量纲分析

对一定的弹靶系统，侵彻效率反映了弹体侵彻深度随撞击速度的变化规律。根据理论分析，影响侵彻效率的因素很多，包括弹体参数、靶体参数及弹体运动参数。相互关联的参数可以省略，弹体垂直侵彻混凝土靶的侵彻效率可简化为：

(1)

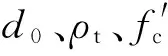
(2)

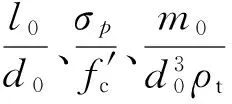
(3)

表2中，低强度弹体和长径比为4的弹体有效实验数据较少，因此利用高强度弹体的5组实验数据，得到量纲一的速度和侵彻效率，见表3。

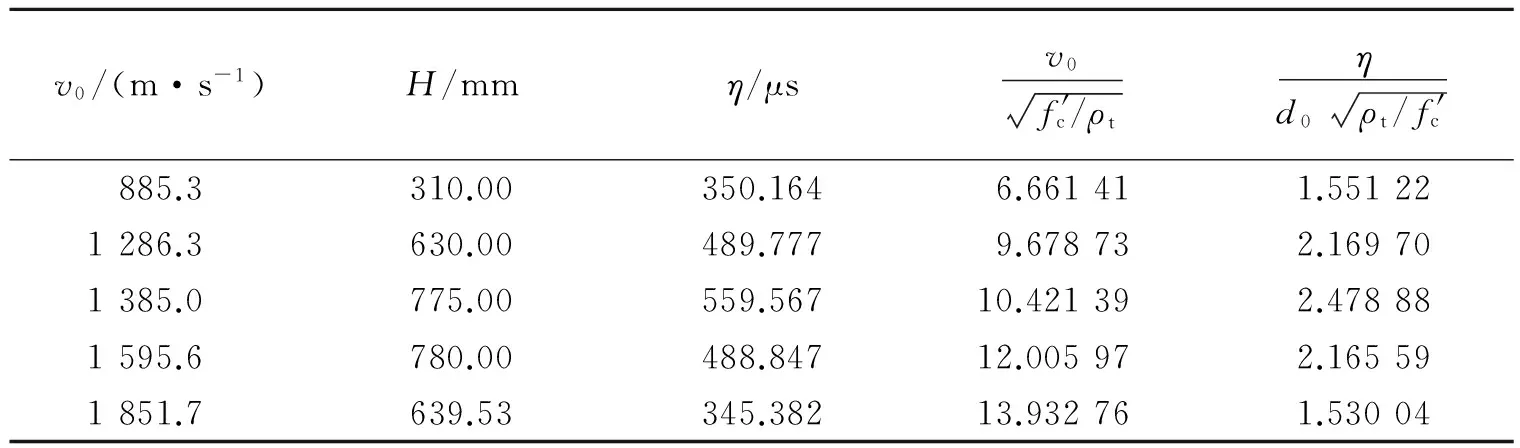
表3 侵彻实验数据Table 3 Penetration experiment data

求解方程，得到高强度弹体量纲一的侵彻效率和弹体撞击速度的具体函数关系式为：

(4)

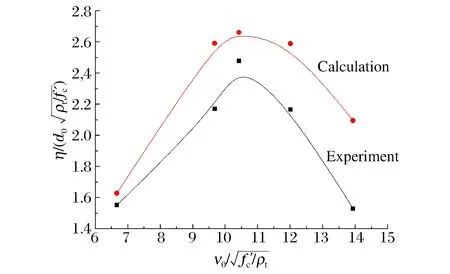
图10 量纲一侵彻效率随量纲一速度的变化Fig.10 Variation of dimensionless penetration efficiency with dimensionless impact velocity

当给定弹体结构、材料及靶体材料时，由式(4)可得到不同弹体撞击速度所对应的侵彻效率，进而预估弹体不同运动条件时的侵彻能力。图10为量纲一侵彻效率随量纲一速度变化曲线的计算与实验结果对比。可以看出，计算的侵彻效率随速度的变化规律与实验数据相符，对于30 mm口径弹体高速侵彻素混凝土靶，当撞击速度为1 371 m/s(量纲一速度为10.316)时，计算侵彻效率达到极值，实验最大侵彻效率对应的速度为1 400 m/s，误差为2%；计算的最大侵彻效率比实验偏大约10%，说明模型计算结果与实验数据较吻合，也就证实了式(4)的有效性。

3 结 论

开展了30 mm口径弹体的高速侵彻实验，取得了撞击速度高达约1 900 m/s的高速侵彻实验结果，得到了撞击速度、弹体强度、弹体长径比等参数对弹体侵蚀和侵彻效率的影响规律，对实验结果进行分析总结，得出以下结论。

(1)侵彻效率随着撞击速度v0的增大先增大后减少，当v0接近vmax时，侵彻效率达到极值，此时侵彻深度虽然还未达到最大值，但已接近极值。这两种材料强度的弹体，最大侵彻效率对应的vmax分别为1 050和1 400 m/s，v0再提高5%左右时，H达到极值。

(2)质量侵蚀主要集中在弹体头部，弹体圆柱部分的长度和直径在侵彻过程中几乎没有减少，当弹体材料强度提高至约2倍时，质量侵蚀率降低约80%。

(3)根据高强度弹体实验数据，得到了量纲一的侵彻效率和弹体撞击速度的函数关系式，能够根据实验的具体弹靶条件，估算最大侵彻效率对应的弹体撞靶速度，为高速侵彻效应模拟实验提供了参考。

本文中的量纲一侵彻效率模型仅考虑了弹体撞击速度的影响，而弹体材料强度、长径比、靶体强度等的影响也较大，今后要结合更多的高速侵彻实验，开展相关的修正与改进工作。

[1] 宋梅利，王晓鸣，赵希芳，等.弹体高速侵彻混凝土靶侵彻效率影响因素分析[J].南京理工大学学报，2014,38(3):390-395. Song Meili, Wang Xiaoming, Zhao Xifang, et al. Influencing factors of penetration efficiency for projectiles’ high-speed penetration into concrete targets[J]. Journal of Nanjing University of Science and Technology, 2014,38(3):390-395.

[2] Nelson R W. Low-yield earth-penetrating nuclear weapons[J]. Science and Global Security, 2002,10(1):1-20.

[3] Forrestal M J, Frew D J, Hanchak S J, et al. Penetration of grout and concrete targets with ogive-nose steel projectiles[J]. International Journal of Impact Engineering, 1996,18(5):465-476.

[4] Forrestal M J, Altman B S, Cargile J D, et al. An empirical equation for penetration depth of ogive-nose projectiles into concrete targets[J]. International Journal of Impact Engineering, 1994,15(4):395-405.

[5] Davis R N, Neely A M, Jones S E. Mass loss and blunting during high-speed penetration[J]. Proceedings of the Institution of Mechanical Engineers: Part C, 2004,218(9):1053-1062.

[6] Mu Z C, Zhang W. An investigation on mass loss of ogival projectiles penetrating concrete targets[J]. Intrnational Journal of Impact Engineering, 2011,38(8):770-778.

[7] Chen X W, Li Q M. Transition from non-deformable projectile penetration to semi-hydrodynamic penetration[J]. Journal of Engineering Mechanics, 2004,130(1):123-127.

[8] 谢多夫.力学中的相似方法与量纲理论[M].沈青,倪锄非,李维新,译.北京：科学出版社,1982.

[9] Chen X W, He L L, Yang S Q. Modeling on mass abrasion of kinetic energy penetrator[J]. European Journal of Mechanics A: Solids, 2010,29(1):7-17.

(责任编辑 丁 峰)

Experiments and dimensional analysis of high-speed projectile penetration efficiency

Song Meili, Li Wenbin, Wang Xiaoming, Feng Jun, Liu Zhilin

(MinisterialKeyLaboratoryofZNDY,NanjingUniversityofScienceandTechnology,Nanjing210094,Jiangsu,China)

This paper carried out high-speed penetration experiments using semi-infinite plain concrete targets with different projectile materials and aspect ratios to investigate the effects of striking velocity and material strength on projectile loss and penetration efficiency. Characterized with caliber-radius-head (CRH) 3.0 and 30-mm diameter, the ogive-nose projectiles were launched at high-speed striking velocities between 880-1 900 m/s to impact the concrete target. The measured experiment data indicates that the penetration efficiency is in parabolic relation with the striking velocity, i.e. the maximum penetration efficiency corresponds to an impact velocity of about 1 400 m/s. The main abrasion occurs around the projectile nose while only negligible erosion is observed at the projectile shank and end cap. When the speed exceeds the characteristic impact velocity, the projectile’s mass loss is so serious that even bending deformation or disintegration occurs. When the projectile strength is nearly doubled, the mass loss is reduced by about 80%. Based on the experimental data, the relationship function of dimensionless penetration efficiency and impact velocity was achieved using dimensional analysis. The dimensionless model obtained in this paper is capable of predicting the corresponding impact speed for the maximum penetration efficiency, thereby providing theoretical guidance for high-speed simulated penetration experiments.

mechanics of explosion; penetration efficiency; high-speed penetration; concrete target; mass erosion; dimensional analysis

10.11883/1001-1455(2016)06-0752-07

2015-04-13； < class="emphasis_bold">修回日期：2016-01-06

2016-01-06

国家自然科学基金项目(51278250)

宋梅利(1975— )，女，博士研究生，副教授，songml75@yahoo.com。

O385 <国标学科代码：1303520 class="emphasis_bold"> 国标学科代码：1303520 文献标志码：A国标学科代码：1303520

A