平面碰撞与强激光加载下金属铝的层裂行为*

翟少栋,李英华,彭建祥,张祖根,叶想平,李雪梅,张 林

(中国工程物理研究院流体物理研究所冲击波物理与爆轰物理重点实验室，四川 绵阳 621999)

平面碰撞与强激光加载下金属铝的层裂行为*

翟少栋,李英华,彭建祥,张祖根,叶想平,李雪梅,张 林

(中国工程物理研究院流体物理研究所冲击波物理与爆轰物理重点实验室，四川 绵阳 621999)

在轻气炮和神光Ⅱ强激光装置上开展了金属铝的层裂实验。针对激光打靶层裂实验中样品自由面速度剖面后期振荡容易丢失问题，改进靶设计，获得很好效果。利用轻气炮加载和强激光加载层裂实验应变率的显著差异，并通过数值模拟，讨论了在建立具有预测能力的理论建模中需要关注的损伤成核、演化与汇合问题中的材料特性与应变率相关特性因素。结果表明，对于我们以前建立的动态损伤与断裂模型，微孔洞成核的平均半径、阈值压力、成核速率相关参数以及微孔洞长大的阈值压力等具有材料特性属性，但微孔洞的表面能以及决定材料发生完全层裂的临界损伤度等具有明显的应变率效应。另外，分析还发现，虽然层裂强度具有明显的应变率效应，但是在样品层裂当地，样品由持续拉伸向收缩转变的临界行为，取决于一个很小的临界损伤，这个临界值很可能是材料常数，与应变率无关。

固体力学；动态损伤与破坏；碰撞；金属铝；层裂；强激光

材料的动态损伤与破坏是冲击波物理领域的一个重要科学问题，在国防和民用领域存在重要应用。几十年以来，尽管人们对材料的动态损伤与破坏开展了大量研究，特别是针对层裂问题[1-8]，但目前对这个问题进行科学预测依然非常困难。为了发展具有预测能力的理论模型，充分认识和理解动态损伤累积过程中的材料特性因素以及应变率相关因素非常重要。过去的研究主要通过平面碰撞层裂实验来进行，平面碰撞的拉伸应变率一般在104～105s-1量级，虽然可以通过调整碰撞速度以及飞片和样品的尺寸，实现一定程度的应变率变化，但变化的范围非常有限。这对于检验和揭示有关因素的材料特性或应变率相关特性，是一种局限。随着强激光技术的发展，利用强激光烧蚀加载相对平面碰撞加载，应变率可以有2个以上的量级差，达106～109s-1量级。因此，研究平面碰撞与强激光加载下材料的层裂行为，对于认识和理解动态损伤有关影响因素的材料特性和应变率相关特性，以及检验理论模型的描述或预测能力，并揭示有关不足，具有重要意义。本文中，在轻气炮以及神光Ⅱ装置上开展金属纯铝的层裂实验，针对激光打靶层裂实验样品自由面速度剖面后期振荡容易丢失问题，改进靶设计，运用张林等[9-10]建立的金属材料的动态损伤与破坏理论模型，对实验进行数值模拟，以此分析微损伤成核、长大以及汇合过程中的材料特性因素和应变率相关因素，并探讨进一步提高该理论模型的预测能力问题。

1 层裂实验

图1是平面碰撞实验装置的示意图。实验由一级轻气炮发射飞片与样品碰撞。飞片与样品均为99.99%的纯铝，飞片厚度3 mm，样品厚度6 mm，飞片与样品的直径大于60 mm，满足一维应变条件要求[11]。飞片击靶速度由刷子电探针测量，样品自由面速度剖面由DPS[12]测量。飞片击靶速度测量结果为0.32 km/s，样品自由面速度测量结果如图3(a)中的绿色虚线所示。

图2是强激光打靶的实验装置。实验在高功率激光物理联合实验室的神光Ⅱ(SGⅡ)装置上进行，由第9路发射一束经束匀化、波长351 nm、脉宽2.95 ns、总能量585 J的强脉冲对靶进行直接烧蚀加载。靶采用4层结构，在烧蚀面是150 μm的CH材料(聚对二甲苯C8H8)，接下来的3层依次为铝、CH和铝，每层厚度均为150m。铝的纯度同样为99.99%。为了提高激光的能量利用率，在烧蚀面还镀了一层100 nm厚的铝膜。这里采用多层靶设计，因为我们发现前人开展的激光直接烧蚀铝靶层裂实验中，样品自由面速度剖面后期的层裂振荡信号比较容易丢失[13-14]。我们认为，可能是层裂片太薄，与其细观不均匀的尺度可比，从而由细观不均匀性引起的复杂波系相互作用导致预期的振荡信号在极短的时间内(可能亚纳秒尺度)弥散消失，甚至可能导致层裂片破碎，无法继续测量。实际上，层裂振荡信号的幅度含有层裂片损伤程度的重要信息，所以我们设计了上述多层靶结构，期望通过对加载波形的整形以及层裂片厚度的提高，获得明显的层裂振荡信号，实际结果令人满意。上述多层靶设计有以下几个优点：第1层CH膜可以降低压缩波和追赶稀疏波的陡度，有利于提高层裂片厚度；第2层CH膜可以抑制压缩波阵面的不平整性，弱化复杂波系相互作用的强度；另外，整个靶厚度增加，追赶稀疏波传播路径变长，可有效展宽稀疏波宽度，更有利于提高层裂片厚度。本次实验中，第9路的聚焦焦斑为2 mm×1.5 mm，为了提高烧蚀面积，采用了离焦烧蚀方案，焦平面调节至烧蚀面前约2 mm。样品自由面速度剖面的测量，采用冲击波物理和爆轰物理重点实验室的双外差测速技术(DLHV)[15]，该技术比DPS有更高的时间分辨能力。实验测量的样品自由面速度剖面如图3(b)中的绿色虚线所示。

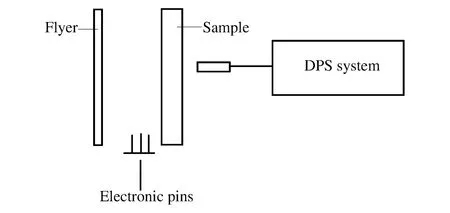
图1 平面碰撞层裂实验装置Fig.1 Setup for plate-impaction experiment

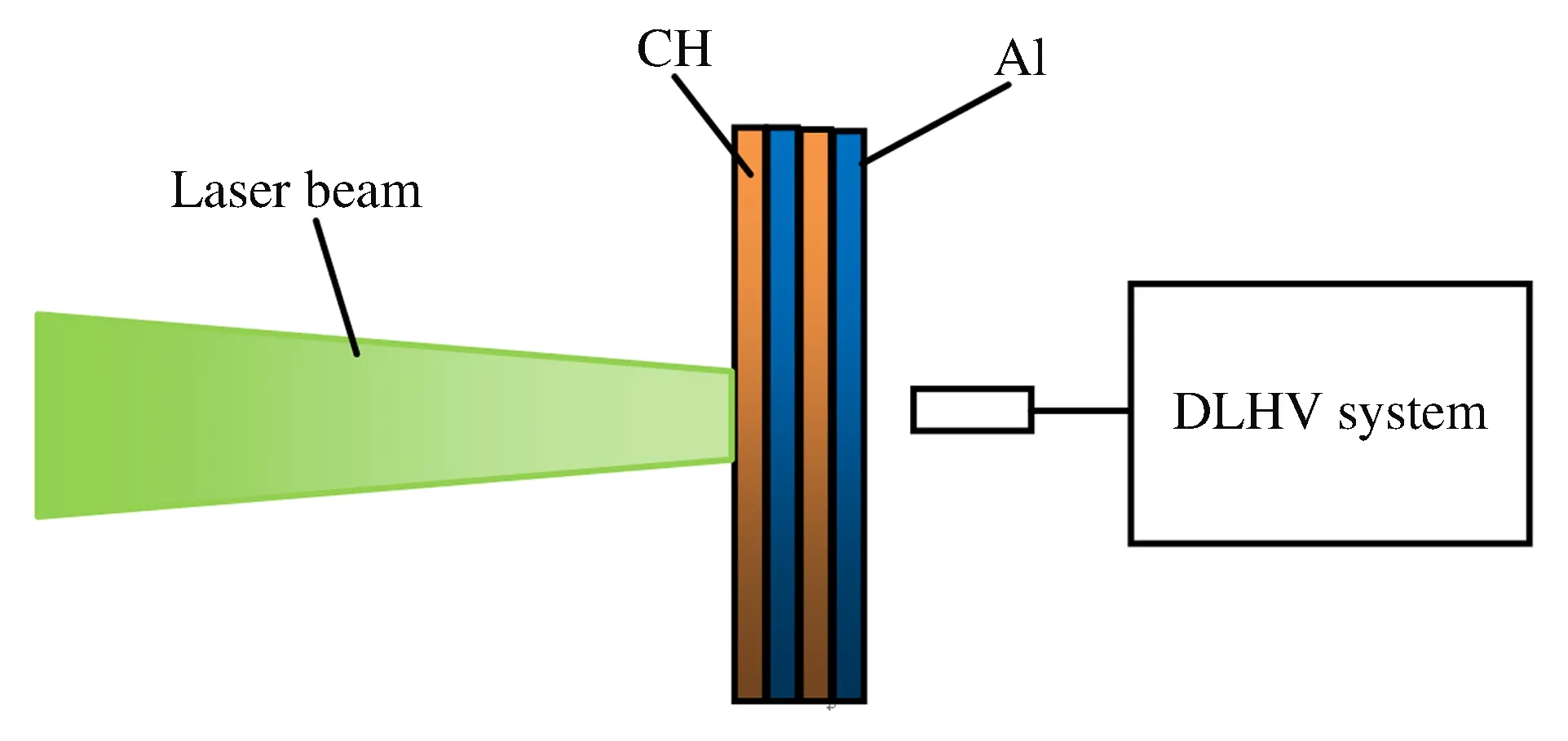
图2 激光打靶层裂实验装置Fig.2 Setup for laser-loaded experiment

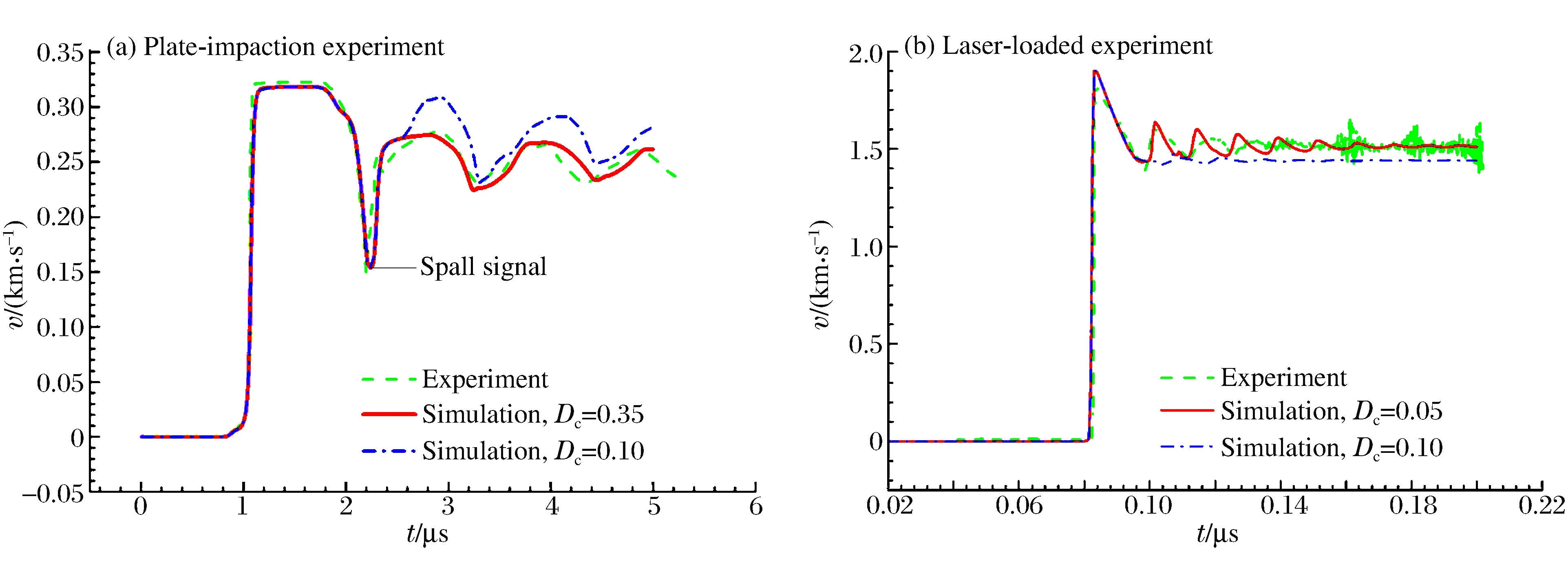
图3 样品自由面速度剖面Fig.3 Free surface velocity profiles

2 数值模拟

金属铝的材料模型采用弹塑性模型，本构关系使用John-Cook经验关系式[16]：

(1)

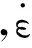
CH材料则采用流体模型。

铝和CH材料的物态方程均使用Grüneisen物态方程，并应用γ/v=γ0/v0为常数的近似[17]：

(2)

(3)

eH=e0+0.5(pH+p0)(v0-v)

(4)

式中：pH和eH为Hugoniot绝热线。ρ0、v0、e0为初始状态的密度、比容以及内能，c0、λ为冲击波速度与波后粒子速度间的线性关系系数。调整零点能，使e0为零。

材料的动态损伤与破坏，采用张林等[9-10]的理论模型。定义损伤内变量D为：

(5)

式中：Vv为孔洞体积，Vt为总的体积。对时间求导，有：

(6)

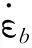
(7)

式中：Rn为孔洞成核的平均半径，ρm为基体密度，N0为与成核速率相关的参数，pm为基体中的压强，p0为成核阈值压强，p1为具有压强量纲的模型参数。

孔洞长大过程中，假定周边基体释放的体积形变能转换为孔洞长大新增的表面能，可推得：

(8)

式中：Cmb为基体的体波声速，Bm为基体的体模量，σ0为微孔洞长大的阈值压强，λD为孔洞的表面能。

损伤对材料的软化，采用J.K.Mackenzie提出的关系式[18]：

(9)

(10)

式中：Gm和Bm分别为损伤后基体的剪模量和体模量，G和B为不含损伤时材料的剪模量和体模量。

模型中，假定当损伤达到某个临界值Dc时，孔洞迅速汇合至贯穿，样品发生完全层裂。

平面碰撞层裂实验的模拟，由自编一维程序包DRSC(dynamic response simulation code)进行；激光烧蚀层裂实验的模拟，先用程序包Multi[19]通过输入实测的激光脉冲波形计算烧蚀面的压力剖面，再将该压力剖面作为输入量输入DRSC，对样品的动态响应行为进行模拟。表1列出了使用的物态方程和本构参数，其中Al的本构参数通过Hopkinson杆实验测定。由于缺乏高温本构数据，这里忽略了冲击压缩引起的温度软化效应(取m=0)，考虑到样品经历的冲击压力远低于其冲击熔化压力，忽略的影响非常有限。Al的物态方程参数取自文献[20]中的Hugoniot数据。CH材料尚无Hugoniot数据，而其实测密度为1.1 g/cm3，因此其Hugoniot参数借用文献[20]中与其密度最接近的ADIPRENE塑料的参数。动态损伤与破坏模型的参数，则由理论对实验的拟合确定，见表2。理论模拟的样品自由面速度剖面，如图3中的红色实线所示，理论与实验比较，两者符合很好。

表1 材料本构参数与物态方程参数Table 1 Parameters of constitutive relation and equation of state

表2 损伤参数Table 2 Parameter values for the dynamic damage and fracture model

3 结果与讨论

模拟表明，平面碰撞实验样品层裂发生于距离样品自由面3.03 mm区域，激光加载实验的则发生于距离样品自由面33 μm区域。图4～5分别给出了两发实验层裂当地的压强、比容以及损伤内变量的演化。为便于讨论，基于模拟结果，按下式估算实验样品层裂当地拉伸过程的平均应变率：

(11)

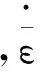
动态损伤与破坏模型中，有7个模型参数，分别是N0、p0、p1、Rn、σ0、λD和Dc。其中N0、p0、p1、Rn、σ0等5个参数具有材料特性属性，为材料常数。两发实验的数值模拟中，这5个参数值不变，两者模拟结果均较高程度与实验符合。说明在105～107s-1应变率范围内，有关这5个参数的模型近似可以接受，具备一定的预测能力，经标定实验确定参数值后可延展使用。

在概念上，参数λD是微孔洞增加单位面积所消耗的能量，具有表面能量纲。但是，该能量由微孔洞长大过程中基体释放的体积形变能提供，而更严格地，基体释放的体积形变能仅一部分转化为微孔洞的表面能，更多部分转化为基体收缩的局域动能和其他形式能，且局域动能最终将被耗散转化为基体的内能。一般地，应变率越高，转化为局域动能所占的比例越大，因此实际上λD是一个有效量，与应变率严重相关。在模型中，参数Dc的物理意义是：当样品某位置处的损伤变量达到该临界值后，样品在该位置的微孔洞在一个可忽略的时间尺度内快速完成汇合，并贯穿使样品发生完全层裂，因此该参数同样严重应变率相关。表2中，激光打靶实验的λD远大于平面碰撞实验的，Dc远小于平面碰撞实验的，与上述理解一致。这个结果表明，提高该模型的预测能力，必须进一步研究λD和Dc与应变率等因素的依赖关系，我们以后将对此开展研究。

前面曾阐述，对于材料的动态损伤与破坏，层裂实验样品自由面速度剖面后期的振荡，其幅度反映了材料的损伤程度，具有重要意义。图3中的蓝色点划线分别为Dc比合适值更小和更大情况下的模拟曲线，说明：Dc偏小时，剖面的振荡幅度将增大；Dc偏大时，振荡幅度会减小，甚至消失。这表明，利用激光烧蚀加载研究材料的层裂时，采取适当措施，增大层裂片厚度，确保该厚度明显大于材料细观结构及加载波形的不均匀尺度，以便测量能够捕获明显的层裂振荡信号，对于层裂研究具有重要价值。

由图4～5，最大负压分别为1.92和2.92 GPa，这说明层裂强度的应变率效应非常明显。值得注意的是，当应力剖面出现回弹时，相对应的D分别为0.000 56和0.000 55，两者高度一致。这揭示，在金属铝的动态损伤与破坏中，样品由持续拉伸向回缩转变的临界行为，取决于一个非常小的临界损伤值，而且这个值可能具有材料属性，是材料常数。考虑到铝的一般性，其他材料可能也存在这个特性。

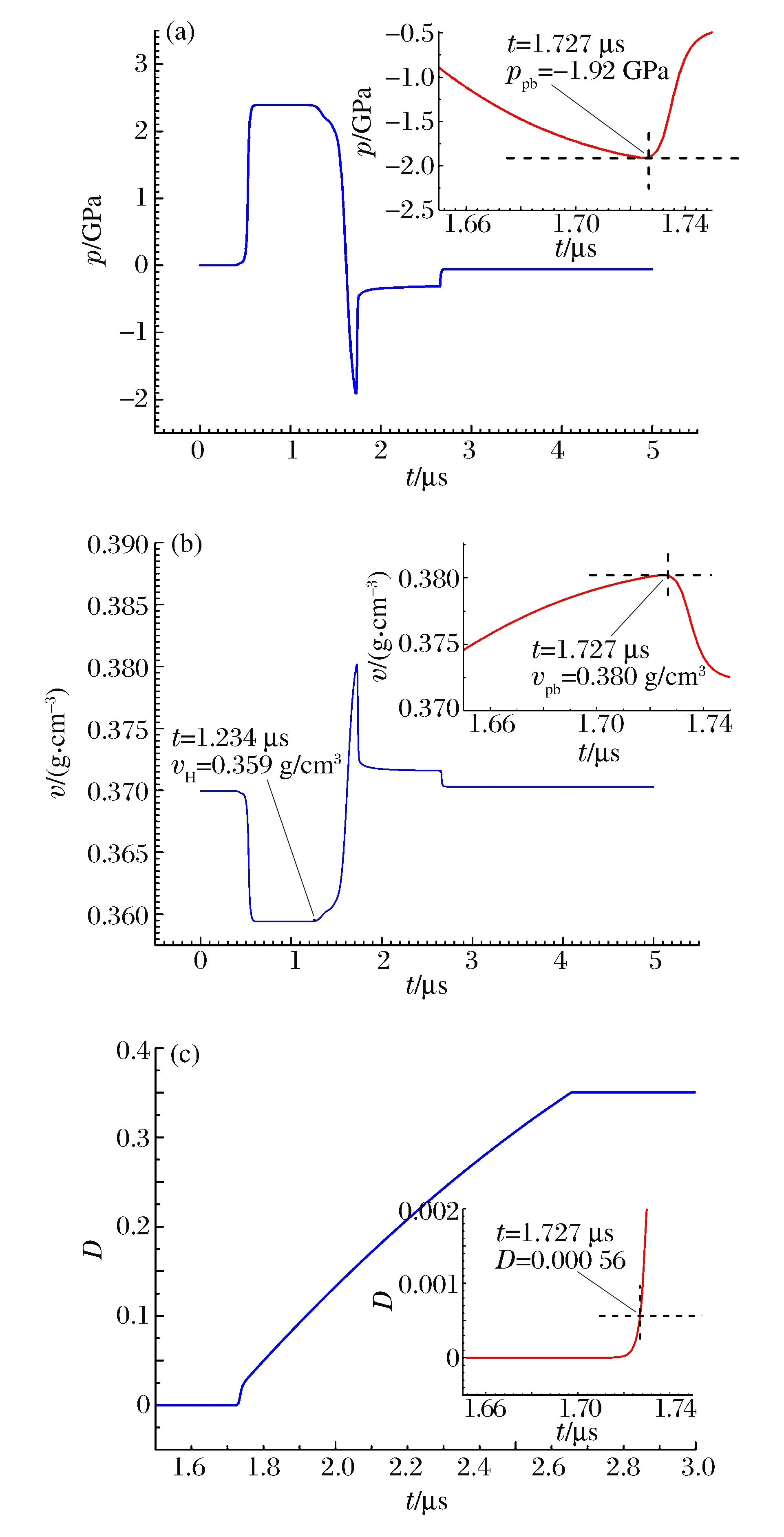
图4 平面碰撞实验样品层裂当地的压强、比容和损伤内变量Fig.4 Pressures, specific volumes and damages at spall position of plate-impact experiment

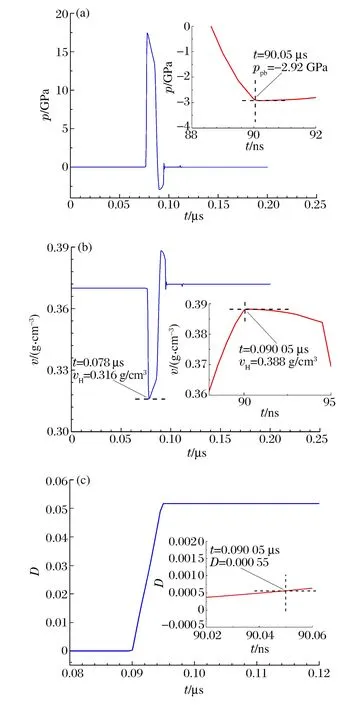
图5 激光打靶实验样品层裂当地的压强、比容和损伤内变量Fig.5 Pressures, specific volumes and damages at spall position of laser-loaded experiment

4 总 结

结合实验与数值模拟研究了金属纯铝在应变率相差两个量级条件下的层裂问题，重点应用张林[9-10]的理论模型，讨论了损伤成核、演化与汇合中的材料特性因素与应变率相关因素。分析表明，微孔洞成核的平均半径、阈值压力、成核速率等相关参数，以及微孔洞长大的阈值压力等具有材料特性参数，可通过标定实验确定后延展使用，但微孔洞的表面能以及决定材料发生完全层裂的临界损伤度等具有明显的应变率效应，要提高模型的预测能力的话，需要对他们开展进一步的研究。分析还说明，在层裂过程中，样品由持续拉伸向回缩转变的临界行为，取决于一个临界损伤值，而且这个临界值具有材料属性，是材料常数。另外，对于利用强激光加载开展层裂实验，实验表明，采取适当措施，增大层裂片厚度，确保该厚度明显大于材料细观结构以及加载波形的不均匀尺度，是非常必要的。

感谢高功率激光物理联合实验室华能、陈明提供的帮助！

[1] Curran D R, Seaman L, Shockey D A. Dynamic failure of solids[J]. Physics Reports, 1987,147(5):253-388.

[2] 白以龙,柯孚久,夏蒙梦.固体中微裂纹系统统计演化的基本描述[J].力学学报,1991,23(3):290-298. Bai Yilong, Ke Fujiu, Xia Mengmeng. Formulation of statistical evolution of microcracks in solids[J]. Chinese Journal of Theoretical and Applied Mechanics, 1991,23(3):290-298.

[3] 黄筑平,杨黎明,潘客麟.材料的动态损伤和失效[J].力学进展,1993,23(4):433-467. Huang Zhuping, Yang Liming, Pan Kelin. Dynamic damage and failure of materials[J]. Advances in Mechanics, 1993,23(4):433-467.

[4] 陈永涛,唐小军,李庆忠,等.纯铁材料的冲击相变与“反常”层裂[J].爆炸与冲击,2009,29(6):638-641. Chen Yongtao, Tang Xiaojun, Li Qingzhong, et al. Phase transition and abnormal spallation in pure iron[J]. Explosion and Shock Waves, 2009,29(6):638-641.

[5] 陈永涛,唐小军,李庆忠.Fe基α相合金的冲击相变及其对层裂行为的影响研究[J].物理学报,2011,60(4):046401. Chen Yongtao, Tang Xiaojun, Li Qingzhong. Phase transition and influence of phase transition on spall in α phase Fe-based alloy[J]. Acta Physica Sinica, 2011,60(4):046401.

[6] 章杰,苏少卿,郑宇,等.改进SPH方法在陶瓷材料层裂数值模拟中的应用[J].爆炸与冲击,2013,33(4):401-407. Zhang Jie, Su Shaoqing, Zheng Yu, et al. Application of modified SPH method to numerical simulation of ceramic spallation[J]. Explosion and Shock Waves, 2013,33(4):401-407.

[7] 彭辉,李平,裴晓阳,等.动态损伤演化的空间不连续性实验研究[J].物理学报,2013,62(22):226201. Peng Hui, Li Ping, Pei Xiaoyang, et al. Experimental study of the spatial discontinuity of dynamic damage evolution[J]. Acta Physica Sinica, 2013,62(22):226201.

[8] 贺红亮.动态拉伸断裂的物理判据研究[J].高压物理学报,2013,27(2):153-161. He Hongliang. Physical criterion of dynamic tensile fracture[J]. Chinese Journal of High Pressure Physics, 2013,27(2):153-161.

[9] 张林.延性材料冲击响应:动态损伤与断裂、结构相变的新模型[D].绵阳：中国工程物理研究院,2005.

[10] Zhang Lin, Cai Lingcang, Li Yinglei, et al. Simplified model for prediction of dynamic damage and fracture of ductile materials[J]. International Journal of Solids & Structures, 2004,41(24):7063-7074.

[11] 张林,李英华,陈大年,等.GJB7368-2011 金属材料层裂强度测量方法[S].2011.

[12] Li Xuemei, Yu Yuying, Li Yinghua, et al. Window corrections of Z-cut quartz at 1 550 nm under elastic, uniaxial compression up to 10 GPa[J]. Journal of Applied Physics, 2011,109(10):103518.

[13] 王永刚,Boustie M,贺红亮,等.强激光辐照下纯铝动力学响应和层裂的数值模拟[J].强激光与粒子束,2005,17(9):1281-1285. Wang Yonggang, Boustie M, He Hongliang, et al. Numerical simulation of damage evolution on mechanical behavior and tensile spallation of pure aluminium under laser shock loading[J]. High Power Laser and Particle Beams, 2005,17(9):1281-1285.

[14] 王永刚,Boustie M,贺红亮,等.强激光辐照下纯铝的力学响应和层裂的实验测量与分析[J].强激光与粒子束,2005,17(7):966-970. Wang Yonggang, Boustie M, He Hongliang, et al. Experimental study on mechanical behavior and tensile spallation of pure aluminum under laser shock loading[J]. High Power Laser and Particle Beams, 2005,17(7):966-970.

[15] 陶天炯,翁继东,王翔.一种双光源外差测速技术[J].光电工程,2011,38(10):39-45. Tao Tianjiong, Weng Jidong, Wang Xiang. A dual laser heterodyne velocimetry[J]. Opto-Electronic Engineering, 2011,38(10):39-45.

[16] Johnson G R, Cook W H. A constitutive model and data for metals subjected to large strain，high strain rates and high temperatures[C]∥Proceedings of Seventh International Symposium on Ballistics. The Netherlands, 1983.

[17] Meyers M A. Dynamic behavior of materials[M]. John Wiley & Sons, 1994.

[18] Mackenzie J K. The elastic constants of a solid containing spherical holes[J]. Proceedings of the Physical Society, 1950,63(1):2-11.

[19] Ramis R, Schmalz R, Meyer-Ter-Vehn J. MULTI: A computer code for one-dimensional multigroup radiation hydrodynamics[J]. Computer Physics Communication, 1998,49(3):475-505.

[20] Marsh S P. LASL shock Hugoniot data[M]. University of California Press, 1980.

(责任编辑 丁 峰)

Spall behavior of pure aluminum under plate-impact and high energy laser shock loadings

Zhai Shaodong, Li Yinghua, Peng Jianxiang, Zhang Zugen,Ye Xiangping, Li Xuemei, Zhang Lin

(NationalKeyLaboratoryofShockWaveandDetonationPhysics,InstituteofFluidPhysics,ChinaAcademyofEngineeringPhysics,Mianyang621999,Sichuan,China)

Spall experiments of pure aluminum were performed on the light-gas gun equipment and SG Ⅱ high energy laser facility. An improved target configuration was applied to address the problem that the residual vibration was often lost in laser-loading spall experiments. By virtue of distinguishing the obvious difference in the strain rate between the two experiments, the material and rate-dependent issues related with the nucleation, growth and coalescence of micro-damage were examined using numerical simulations, which is important for developing predictive theoretical models. Results show that for our previously proposed model the average diameter,the critical pressure, and the nucleation rate parameter for micro-void nucleation can be regarded as material constants and the same is true with the critical pressure for micro-void growth, whereas the specific effective surface energy for micro-void growth and the critical damage for coalescence are typical rate-dependent. Furthermore,our simulations indicate that at the local spall position, although the spall strength has an apparent strain rate effect, the critical behavior of the transformation of the sample from continuous stretch to compression is determined by a critical damage, whose value is very small and is probably a material constant.

solid mechanics; dynamic damage and fracture; impaction; pure aluminum; spall; high energy laser

10.11883/1001-1455(2016)06-0767-07

2015-04-15； < class="emphasis_bold">修回日期：2015-05-07

2015-05-07

国家自然科学基金项目(11272293)；国防基础科学研究计划项目(B1520132001)； 冲击波物理与爆轰物理重点实验室基金项目(9140C670301140C67283)

翟少栋(1986— )，男，硕士研究生;

张 林,zhanglinbox@263.net。

O346.1 <国标学科代码：1301545 class="emphasis_bold"> 国标学科代码：1301545 文献标志码：A国标学科代码：1301545

A