融合关联规则Apriori和Weighted-Slope One 算法的模型研究

牛俊洁，左 羽，崔忠伟

（1.贵州大学计算机科学与技术学院，贵州 贵阳 550025；2.贵州师范学院数学与计算机科学学院，贵州 贵阳 550018）

融合关联规则Apriori和Weighted-Slope One 算法的模型研究

牛俊洁1，左 羽2，崔忠伟2

（1.贵州大学计算机科学与技术学院，贵州 贵阳 550025；2.贵州师范学院数学与计算机科学学院，贵州 贵阳 550018）

针对于Slope One算法不精确不具有解释性的缺点提出了一种融合关联规则Apriori和Weighted-Slope One的算法模型。利用关联挖掘Apriori找出互相关联的物品集大大提高了Slope One算法的推荐精度。融合后的AW-Slope One的算法在 Movielens数据集上的对比实验结果表明，在数据集稀疏以及邻居数目较少的情况下，平均绝对误差（MAE）大大降低。

频繁模式挖掘；关联规则；线性模型；Apriori算法；Weighted-Slope One算法

引言

随着信息资源的超载式增长，用户对个性化服务需求逐步提高，推荐系统在电子商务、社交网络和新闻推荐等领域已成为不可或缺的技术[1]。个性化推荐系统中，协同过滤（Collaborative filtering，CF）是应用最成功、最广泛的技术之一[1]，但他们需要消耗大量的时间去计算用户和物品相似度。为了提高效率及实时性，Lemire等[2]提出了Slope One算法，其核心思想是：线性回归f（x）=x+b。借助大量用户对item的评分，可以得到任意两个item的回归直线。未评分item由已评分item计算出分值，由计算出来分值的排序做最终推荐。它的优点是算法简单，容易实现，可扩展性也不错，但必须基于评分，如果没有评分，需要构造评分。郑丹等[3]提出一种基于Weighted-Slope One的用户聚类推荐算法,使用改进的K-means方法聚类用户后，利用User-CF搜索最近邻居，结合Slope One为目标用户推荐对应的产品。杜茂康等[4]等融合了领近项目的Slope One算法。胡旭等[5]提出了基于项目属性相似和MapReduce并行化的Slope One算法。田松瑞[6]等提出了基于用户相似度加权的Slope One算法。

这些算法都是在提高算法的精度上做出了一定的贡献，但其关联性和可解释性相对较差。由此本文将推荐系统领域最著名“啤酒与尿布”故事中用到的关联规则策略融合到Slope One算法中，进行这样一个提高推荐效率尝试。关联规则的目的在于从一个数据集中找出项之间的关系，也称之为购物蓝分析（Market basket analysis）。本文提出基于关联规则的Apriori与Weighted-Slope One相结合的推荐算法。根据数据分析整理，挖掘与目标项目N个项目相关值的计算，参与预测的项目、预测项目评分数据都得到优化。为了解决在使用Slope One算法计算预测值时被忽视的项目本身的相似性对项目评分的影响较大的问题，本文将提出用项目关联的相关性来代替传统形式中共同评价过项目的用户数量，此方法不仅计算了用户对目标项目的预测值，更增强了推荐的可信度。

1 相关研究

1.1 Slope One算法模型

（1）

运用（1）式可得到b的取值，而对于重新得到的数据点vnew，可以根据公式wnew=b+vnew得到一个较准确的预测值。直观上我们可用wi和vi差值的平均值来代替求偏移b的公式。

利用上面的直观，我们定义itemi相对于itemj的平均偏差：

（2）

其中，我们可用Sj,i（）统计在同一时间对物品i和j的评分的所有用户的集合，另外，Sj,i（）所包含的元素总数则由card（）表示。通过对itemi相对于itemj的平均偏差的定义，我们便可得到用户u对itemj的预测值，而此功能将由P（u）j,i=deνj,i+ui实现。当把所有这种可能的预测平均起来，可以预测出用户u对物品j的评分：

（3）

其中，Rj表示所有用户u已经给予评分且满足条件（i≠j且Sj,i非空）的item集合。对于足够稠密的数据集，我们可以使用近似：

（4）

把上面的预测公式简化为

（5）

缺点：在使用SlopeOne计算itemi相对于itemj的平均偏差devj,l时，忽略了当使用不同的用户平均所得到的devj,i，其计算结果的精确度和预设有一定的偏差。假设有2000个用户同时评分了itemj和k，而只有20个用户同时评分了itemj和l，那么显然获得的devj,k比devj,l更具有说服力。

1.2 Weighted-Slope One算法模型

所以对最终的平均使用加权进行一个修正，这也就是推荐更为合理的Weighted-SlopeOne[1]推荐算法。

（6）

其中

（7）

1.3 频繁模式挖掘Apriori算法

关联分析又被称作关联挖掘，其旨在大量的数据中搜寻项目集合或对象集合之间的关联[10]。而其关联又由频繁项集（frequentitemsets）和关联规则（associationrules）两种形式构成，其中，频繁项集（frequentitemsets）解释为：经常出现在一块儿的物品的集合[11]。而关联规则（associationrules）则被解释为：暗示两种物品之间可能存在很强的关系。被搜寻出的关联可用支持度与可信度来衡量。一个项目所拥有的支持度（support）常被定义为该项集的记录在数据集中所占的比例。而一个项集的置信度（confidence）被定义为n+1项集的支持度/n项集的支持度。

Apriori的算法在各大领域中得到了广泛应用，是一种最典型的挖掘布尔关联规则频繁项集的算法[13]。其算法的核心的是采用了具有层次分明搜索的迭代方法思想：k-项集用于寻找（k+1）-项集。第一步，搜索出1-频繁项集的集合。记作L1。L1集合的作用是搜索出2-频繁项集的集合L2,而L2的作用的搜素出3-频繁项集L3，以此类推，直到k-频繁项集不能找到[13]。举例说明：

在这里可以理解为用户1购买了I1,I2,I5，用户2购买了I2,I4。

核心思想是：连接步和剪枝步。连接步是自连接，原则是保证前k-2项相同，并按照字典顺序连接。剪枝步，任何的非空子集的频繁项集也肯定是屡次出现的。恰恰相反，如果某一个的候选非空子集不是屡次出现，可判定该候选出现的不频繁，将其删除[14]。

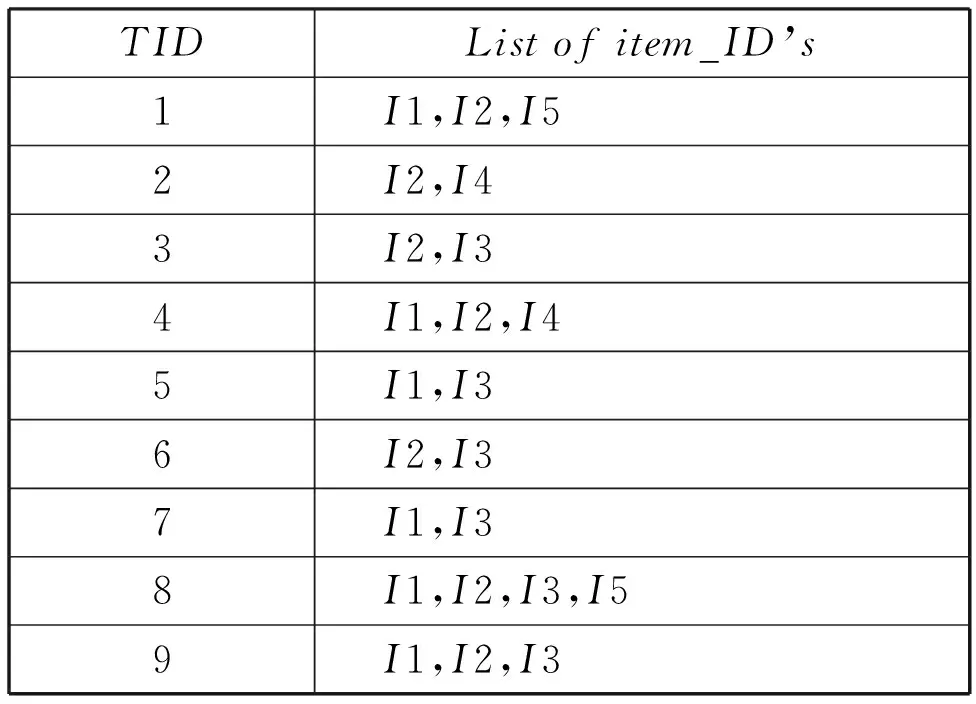
TIDListofitem_ID’s1I1,I2,I52I2,I43I2,I34I1,I2,I45I1,I36I2,I37I1,I38I1,I2,I3,I59I1,I2,I3

图1Apriori算法数据举例

其寻找频繁项集的过程可以用下图来表示：

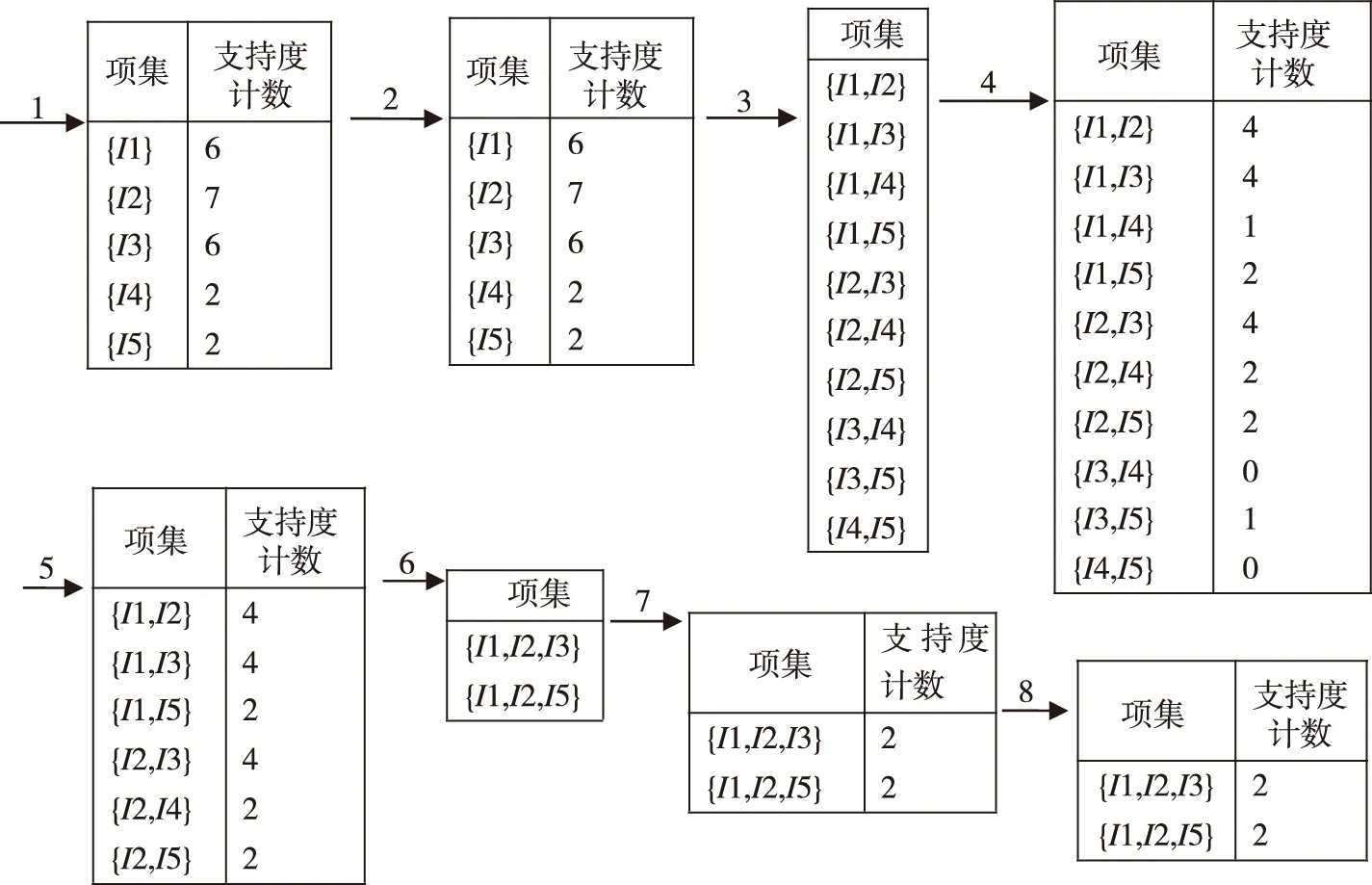
图2 Apriori算法寻找频繁项集的过程

1.扫描D，对每个候选计数得到C1;2.比较候选支持度计数与最小支持度计数，得到L1；3由L1产生候选C2；4.扫描D,对切割候选计数；5.比较候选支持度计数与最小支出度计数得L2；6.由L2产生候选C3；7.扫描D,对每个候选计数得到L3；8.比较候选支持度计数与最小支持度计数。

通过最后的结果我们可以认为，当用户购买物品I1时，很有可能购买物品I2，I3和I5；即物品I1，I2，I3，I5是相关联的。

规则置信度If{I1,I2}then{I3}2/4*100%=50%If{I1,I5}then{I2}2/4*100%=50%

当我们在实际应用中得到相关项之后，我们只需要构建未评分项和其相关项的R（m*n）矩阵，接着使用Weight-SlopeOne算法预测评分即可。

2 算法

2.1 融合关联规则Apriori和Weighted-Slope One算法

在本文提出的算法中，频繁模式挖掘Apriori算法部分，通俗意义就是寻找与目标评分物相近、相关的N个物品。这样就可以缩小计算范围，提高数据可信度，从而达到提高推荐精度的目的。将通过关联规则得到的结果集引入到关联项目置信度为权重的Weighted-SlopeOne算法模型中，计算当前活跃用户对目标项目的打分估计值，最后根据用户对项目评分的预测值高低向用户进行Top-N推荐项目。

2.2 融合关联规则Aprior和Weighted-Slope One算法步骤

关联分析的目标是一个集合的发现和一项规则的发现，即频繁集和关联项集。在Apriori算法中，输入的两个参数依次是最小支持度和数据元素组成的数据集合数。算法的第一个功能是把每一个元素项集列表实现，再对他们进行筛选，把满足要求的留下，不满足的则舍去。随后，把那些不符合条件的集合重新组装起来，形成新的集合。最后，重复上一步所做的操作，并删除不符合最小支持度的集合，一直到所有集合都满足条件。

整个Aprior算法的伪代码如下：

◆当集合中项的个数大于0时

◆构建一个由k个项组成的候选项集的列表（k从1开始）

◆计算候选项集的支持度，删除非频繁项集

◆构建由k+1项组成的候选项集的列表

算法使用python语言完成：

whileTrue:

#循环产生项集大小为1, 2的项集

cur_item_set_size+= 1

ifcur_item_set_size== 1:

#产生初始的候选集

cur_candiate_set=gen_cand_set（data_set, ,cur_item_set_size）

#将候选集分成要满足支持度的集合和不满足支持度的集合，同时记录满足支持度集合对应的支持度分值

saved_item_set,cur_dis_item_set_1,support_data=scan_data_set（data_set,cur_candiate_set,min_support）

else:

#生成该轮候选集

cur_candiate_set=gen_cand_set（data_set,freq_item_set[-1],cur_item_set_size）

#去除候选集中不符合非频繁项集的那些元素

cur_candiate_set,cur_dis_item_set_1 =subtract_item_set（discard_item_set,cur_candiate_set）

#对剩下的候选集，进行遍历数据集，得到保存、丢弃、支持度集合

saved_item_set,cur_dis_item_set_2,support_data=scan_data_set（data_set,cur_candiate_set,min_support）

ifsaved_item_set== :# 如果该轮没有产生任何频繁项集，则下一轮也不会产生新的频繁项集了，退出

break

freq_item_set.append（saved_item_set） #freq_item_set存储每一轮产生的频繁项集

discard_item_set=cur_dis_item_set_1 #discard_item_set存储每一轮产生的要丢弃的项集

discard_item_set.extend（cur_dis_item_set_2）

item_set_support.append（support_data） #item_set_support存储每一轮产生的频繁项集对应的支持度值

3 实验结果与分析

3.1 实验数据集

到grouplens网站（http://www.grouplens.org/node/12）上下载DataSets，在该电影系统中我们使用了将近900多用户为1683的电影评了近100000条的数据集。每个用户看的电影数从1部到20部不等。将下载下来的数据集进行简单处理，保存为u.data，数据格式如图3所示：

电影信息数据集的格式比较复杂，文件名为item.txt这也是一个标签分离的列表，如图4所示：

图3 rating.txt示意图

图4 item.txt的示意图

选第一条记录作为说明:

其中每一个标签所代表的含义分别为：电影id|电影标题|发布日期| |视频IMDbURL|动画|冒险|行动|儿童|喜剧|犯罪|纪录片|戏剧|幻想|黑色|恐怖|音乐|神秘|浪漫|科幻|惊悚|战争|西部

3.2 推荐质量评价指标

对于算法的评估，本文采用了平均绝对误差（MeanAbsoluteTime，MAE）以及平均评估时间（MeanAssessTime，MAT）作为度量标准。

给定一个集合A={p1，p2，D，pE}，并给它赋上新定义“客户评价”，同时定义B={q1，q2，…,qE}）为实际客户评价，则定义MAE是平均绝对偏差，如公式（8）所示：

（8）

3.3 实验过程及结果

实验环境：Python

首先使用Apriori得出频繁项集

图5 利用Apriori算法迭代出频繁项集

再与Weighted-SlopeOne算法结合预测评分并进行Top-N推荐：

图6 结合Weighted-Slope One算法推荐的结果

最后进行算法评估：

图7 各算法的MAT评估折线图

分析实验结果可得：AW-SlopeOne算法相比于W-SlopeOne和SlopeOne算法，平均绝对误差（MeanAbsoluteTime，MAE）数值大大降低；随着数据的增多，MAE的值都在减小。由此得出，本文提出的AW-SlopeOne算法在几乎没有增加评估时间的情况下大大降低了推荐误差率。

4 结束语

本文提出了一种融合关联规则Apriori和Weighted-SlopeOne的算法模型AW-SlopeOne。其策略是首先利用频繁模式挖掘Apriori算法获得一些关联规则，得到频繁项集也就是与未评分项相关的项集构造相关项的轻量级矩阵；再在该轻量级矩阵中使用线性Weighted-SlopeOne算法模型进行评分计算，最后做Top-N推荐。算法评估在Movielens数据集上进行的对比实验显示，MAE平均误差率大大降低。下一步工作可尝试将关联规则Apriori算法替换为FP-Growth探索能否进一步提高推荐精度并降低平均误差率和平均估算时间。

[1]SunH，ZhengZ，ChenJ，etal.PersonalizedWebServiceRecommendationviaNormalRecoveryCollaborativeFiltering[J].IEEETrans.ServiceComputing,2013，6（4）：573-579.

[2]LEMIRED，MACLACHLANA．SlopeOnePredictorsforOnlineRatingBasedCollaborativeFiltering[C]/ /InSIAMDataMining.California:SIAM，2005:21-23.

[3]郑丹，王明扬，陈广胜．基于Weighted-slopeOne的用户聚类推荐算法研究[J]．计算机技术与发展，2016,35（5）:161-165.

[4]杜茂康，刘苗，李韶华等．基于邻近项目的SlopeOne协同过滤算法[J]．重庆邮电大学学报：自然科学版， 2014， 26（3）：421-426．

[5]胡旭，鲁汉榕，陈新,等.基于项目属性相似和MapReduce并行化的SlopeOne算法[J].空军预警学院学报,2015（1）:54-58.

[6]田松瑞.基于用户相似度加权的SlopeOne算法[J].软件，2016，37（4）：57（59.

[7]JIANGTongqiang，LUWei，XIONGHaitao．PersonalizedCollaborativeFilteringBasedOnImprovedSlopeOneAlgorithm[C]/ /2012InternationalConferenceonSystemsandInformatics（ICSAI2012）．Yantai：IEEE， 2012：2312-2315

[8]SUNMingtao,ZHANGHui，SONGShiyu，etal．USO-ANewSlopeOneAlgorithmBasedOnModifiedUserSimilarity[C]/ /2012InternationalConferenceonInformationManagement，InnovationManagementandIndustrialEngineering（ICIII）．Sanya:IEEE，2012：335-340

[9]WANGPu，YEHongwu.APersonalizedRecommendationAlgorithmCombiningSlopeOneSchemeandUserBasedCollaborativeFiltering[C]/ /2009InternationalConferenceonIndustrialandInformationSystems.Haikou：IEEE，2009:152-154.

[10]LopezJ，DahabR.NewPointCompressionAlgorithmsforBinaryCurves[C].InformationTheoryWorkshop,2006.ITW'06PuntadelEste.IEEE，March，2006.

[11]AgrawalR，SrikantR.Fastalgorithmsforminingassociationrules.In：Proc.oftheInt’lConf.onVeryLargeDataBases（VLDB）.Santiago，1994：487-499.

[12]ZakiMJ.Scalablealgorithmsforassociationmining.IEEETrans.onKnowledgeandDataEngineering（TKDE），2000，12（3）:372.

[13]HanJ，PeiJ，YinYW.Miningfrequentpatternswithoutcandidategeneration.In：Proc.oftheACMAnnualConf.onManagementofData（SIGMOD），2000，1（12）.

[14]HanJW，FuYQ.Discoveryofmultiple-levelassociationrulesfromlargedatabases.In：Proc.oftheInt’lConf.onVeryLargeDataBases（VLDB），1995：420-431.

[15]SrikantR，AgrawalR.Mininggeneralizedassociationrules.In：Proc.oftheInt’lConf.onVeryLargeDataBases（VLDB），1995：407-419.

[16]项亮．推荐系统实践[M]．北京:人民邮电出版社，2012．

[17]DietmarJannach,MarkusZanker.推荐系统[M].蒋凡,译.北 京：人民邮电出版社,2013:25-28.

[责任编辑：黄 梅]

Research on integrating association rules Apriori into Weighted- Slope One algorithm

NIU Jun-jie1, ZUO Yu2, CUI Zhong-wei2

（1.College of Computer Science & Information, Guizhou University, Guiyang, Guizhou,550025; 2.School of Mathematics and Computer Science, Guizhou Education University, Guiyang, Guizhou, 550018）

We integrate association rules Apriori into Weighted-Slope One algorithm because the Slope One algorithm is not accurate with explanatory faults .Using association rules Apriori to find related items set has greatly increased recommendation accuracy of the Slope One algorithm.And on Movielens data set of contrast experiment results show that the fusion of AW-Slope One algorithm has greatly reduced the mean absolute time （MAE） even though sparse data sets or the circumstances of less number of neighbors.

Frequent pattern mining; Association rules; Linear model; The Apriori algorithm; Weighted-Slope One algorithm

2016-10-09

2016年贵州省省级重点支持学科“计算机应用技术”（黔学位合字ZDXK[2016]20号）；2016年度贵州省科技平台及人才团队专项资金项目（项目编号：黔科合平台人才[2016]5609）；2016年度省教育厅高校自然科学研究项目（黔教合字[2016]015、黔教合KY字[2016]040）；2015年省级高技术产业示范工程专项（黔发改投资[2015]1588号）。

牛俊洁（1991-），女，山东淄博人，贵州大学2014级在读硕士研究生，研究方向：大数据管理与应用。

TN918；TP309

A

1674-7798（2016）12-0037-06