磁流变减振器的建模与半主动悬架振动控制的研究*

潘公宇，侯观远青，杨 海

(江苏大学汽车与交通工程学院，镇江 212013)

2016115

磁流变减振器的建模与半主动悬架振动控制的研究*

潘公宇，侯观远青，杨 海

(江苏大学汽车与交通工程学院，镇江 212013)

根据磁流变减振器阻尼特性的试验结果，建立了一种将参数化与非参数化建模方法相结合的阻尼力模型。该模型用自适应神经模糊推理系统模拟阻尼力的滞回特性，数值拟合阻尼力随电压和速度而变化的关系。验证结果表明，该模型能很好地逼近试验结果并反映其滞回特性。在此基础上，推导了在理想控制力下所建阻尼力模型的控制电压计算方法，并将该方法应用于汽车的磁流变半主动悬架控制的仿真。结果显示磁流变半主动悬架能较好地提高车辆的平顺性，提出的控制电压计算方法可行有效。

磁流变减振器；建模；半主动悬架；振动控制

前言

磁流变减振器(MRD)是基于磁流变液在磁场作用下流动阻尼可控特性的一种减振装置，具有响应迅速、可调范围大和可控性强等优点。由于磁流变减振器具有强非线性特性，为了充分利用其减振功能，需要能够实时准确地获得理想的控制电压或电流。目前用于磁流变减振器的控制方法主要有Skyhook控制[1]、滑模控制[2]和自适应模糊控制方法等[3-5]，其中Skyhook控制策略只能实现开关控制且会产生自激现象；滑模控制要测量减振器的力；自适应模糊控制计算量大。在控制过程中使用的参数化模型有些拟合效果较差[6-7]，有些非线性较强难以处理[8]；非参数化模型普遍计算量大[9-11]。因此在实际应用中难以获得满意的效果。

本文中在磁流变减振器阻尼特性试验基础上，结合参数化和非参数建模各自的优点提出了一种将参数化与非参数化建模方法相结合的阻尼力模型。用自适应神经模糊推理系统逼近归一化之后的试验数据来描述阻尼力关于活塞杆位移及速度的非线性滞回关系；根据不同工况下的试验结果，拟合出阻尼力关于输入电压和活塞杆速度的关系公式。以该模型为基础研究了实时控制电压的计算方法，并将其应用于2自由度磁流变半主动悬架进行仿真，研究结果表明，本文中所提出的模型是有效的，基于该模型的实时控制电压计算方法是可行的。

1 磁流变减振器阻尼特性建模

1.1 磁流变减振器阻尼特性试验

试验对象为Lord公司的RD-1005型磁流变液减振器。该减振器的工作模式为流动方式，由磁流变液、上下储液腔、活塞组件、励磁线圈、内置补偿气室和导线组成，最大输入电压12V。通过图1所示的激振台驱动减振器缸筒相对于活塞杆做正弦简谐运动，设置激振频率为4Hz，振幅分别为4，10和15mm，输入电压0～7V，间隔1V[11]。试验结果如图2和图3所示，图2中曲线由内到外为电压增大的方向。

图1 磁流变液减振器实际测试图

图2 振幅10mm、频率4Hz时阻尼力-速度曲线

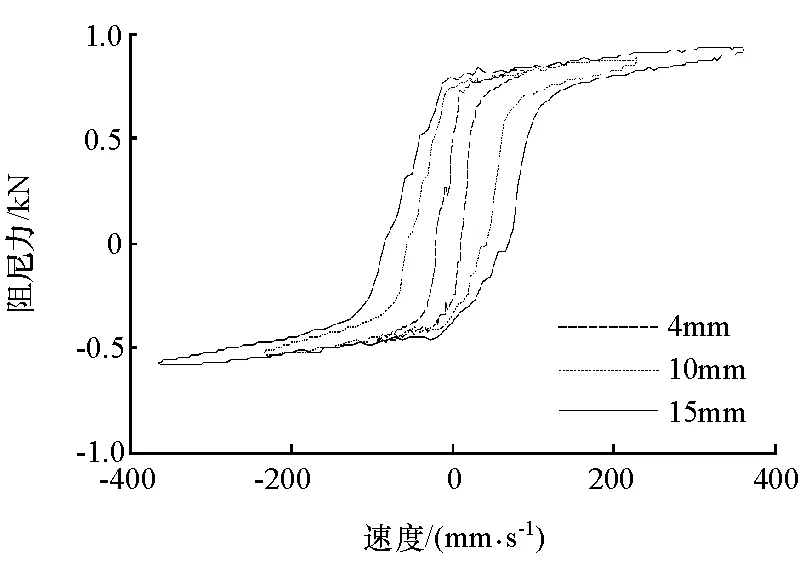
图3 电压2V、频率4Hz时阻尼力-速度曲线

由图2可见，阻尼力随电压的增大而显著增大。这是由于电压增大后线圈产生的磁场强度也变大，液体的剪切应力也因此变大。由图3可见，当输入电压一定时，高速部分的阻尼力呈近似线性变化，只与速度相关，几乎不受振幅变化的影响。阻尼特性曲线在复原行程和压缩行程产生的阻尼力并不关于零点对称，而是整体往上偏移了一定距离，该偏置力是因为减振器内设置有补偿气室造成的。此外，将试验数据去除偏置力影响后进行归一化处理，发现其阻尼特性曲线具有很高的重合度，如图4所示。

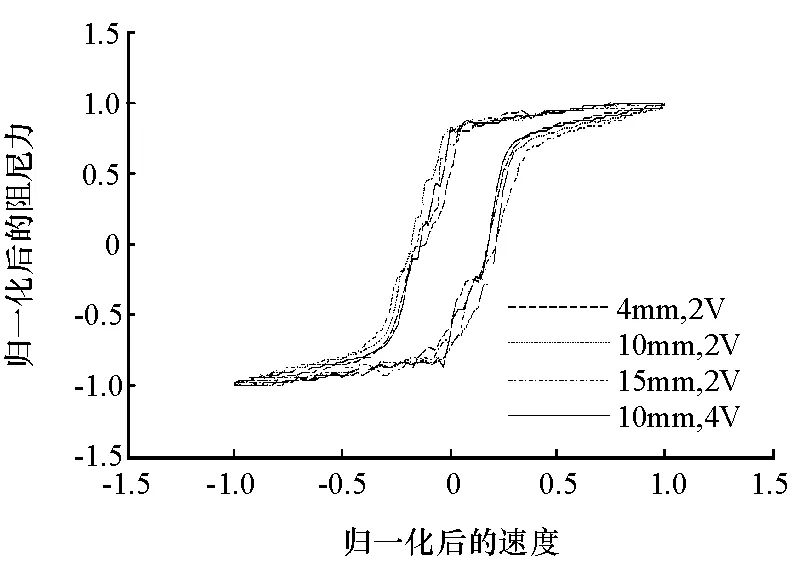
图4 归一化后的阻尼力-速度曲线

1.2 阻尼力模型结构

根据试验结果分析，本文中提出了阻尼力模型结构，如图5所示。该模型主要由两个部分组成。

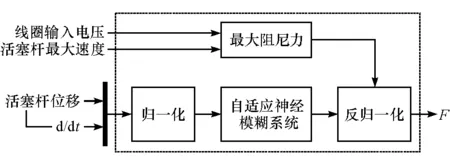
图5 磁流变减振器阻尼力模型结构

(1) 非线性滞回特性描述部分 用自适应神经模糊推理系统逼近归一化之后的试验数据来描述阻尼力的非线性滞回特性。

(2) 最大阻尼力参数拟合部分 根据不同工况下得到的试验数据的最大阻尼力，拟合出减振器最大阻尼力与输入电压和活塞杆最大速度的关系式。此处最大阻尼力是指对应试验工况下阻尼力去除偏置力影响后的最大值。

目前，我国大多数的乡村旅游建设是由政府主导，尤其是在各种扶持政策文件下，得到当地乡镇政府的极大重视，为乡村旅游发展提供了基础保证，但仅靠政府力量并不足够，需要整合行业协会、企业、志愿者、村民等共同形成管理机构，统一规范管理。如借鉴“法兰西最美丽村庄”协会的经营模式，建立严谨的组织结构和管理机制，让本村的干部、提供资助的社团或企业以及部分有经验的并有一定学历的服务行业从业者组成执行代表团，共同参与建设，更多地赋权给对本地区概况极其了解且有一定学历背景的本地村民及有权威性的协会部门或企业，共同参与标准的制订与考核，平衡各相关者的利益，达到利益均衡才是可持续发展的根本动力。

将得到的阻尼力非线性滞回特性逼近结果分别按照最大阻尼力和对应的振幅和最大速度反归一化处理，然后加上阻尼偏置力就可模拟任意输入激励下磁流变液减振器的阻尼力动态特性。

1.3 非线性滞回特性描述

自适应神经模糊推理系统(ANFIS)是一种借用神经网络理论进行模糊系统的参数自整定，充分利用两种理论各自优势的一种自适应网络[12]。ANFIS已被证明能以任意精度逼近连续非线性函数，并用模糊逻辑系统来表达非线性函数。ANFIS的参数学习多采用BP算法或BP算法与最小二乘法结合的混合算法。

将ANFIS设计为双输入单输出系统，以归一化后的位移和速度为系统的输入变量，归一化后的阻尼力为系统的输出变量，隶属度函数均采用三角形隶属度函数，采用输入激励振幅10mm、频率4Hz、输入电压为1～7V时试验数据来进行ANFIS训练。

图6为经过ANFIS训练后的模糊规则曲面图。

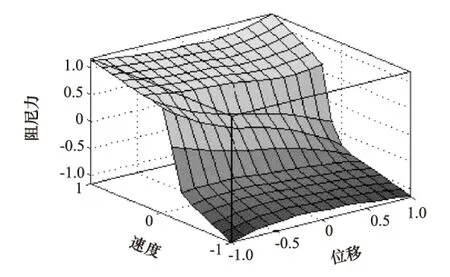
图6 训练后自适应神经模糊系统的控制规则曲面

1.4 最大阻尼力参数拟合

准确地计算减振器在任意激励条件下的最大阻尼力是建立该阻尼力模型重要的一步。参考Bingham力学模型将磁流变减振器的阻尼力看作是由与磁流变液剪切应力相关的库仑阻尼力和与活塞运行速度相关的黏滞阻尼力两部分组成。图7(a)为最大阻尼力与电压的关系，电压越大最大阻尼力随速度的变化幅度也越大，这在阻尼力与速度的关系图上表现为高速部分的斜率随电压的增大而变大；屈服后部分的斜率与电压关系如图7(b)所示；相应的库仑阻尼力与电压的关系如图7(c)所示。

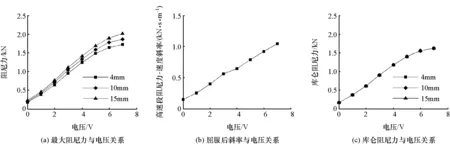
图7 最大阻尼力参数拟合关系曲线

根据以上分析结果，建立最大阻尼力表达式：

Fm= -5.2u3+43.7u2+161.0u+167.5+

(1)

(2)

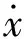
1.5 模型验证

当输入激励振幅为15mm、频率为4Hz、输入电压为0～7V时的模型验证结果如图8和图9所示。由图可见：模型仿真结果能够很好地反映阻尼力的动态特性，虽然有一定误差，特别在速度为0附近的误差要大一些，这些误差一是由于减振器补偿气囊的压力波动和外部扰动而造成的，二是使用试验数据进行自适应神经模糊系统训练也会将试验误差传递至阻尼力模型，但是整体误差控制在较小的范围内。

图8 振幅15mm、频率4Hz时阻尼力-速度曲线

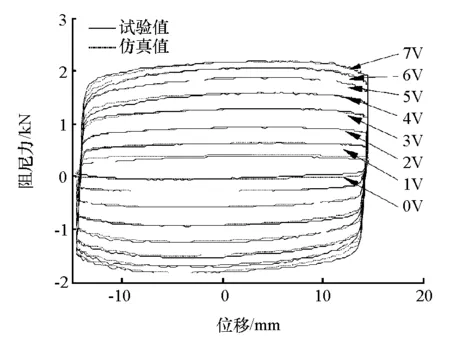
图9 振幅15mm、频率4Hz时阻尼力-位移曲线

验证结果表明，该磁流变液减振器阻尼特性的建模方法是可行的。相比于现有模型，该模型可以避免建模过程出现大量需识别的参数，且不需要大量的试验数据用于训练，大大减少了建模的工作量。由于采用减振器的运动状态作为模型输入，故控制设计更方便，以半主动控制方式调节磁流变液减振器的阻尼力也更容易，从而可更好地发挥磁流变液减振器的减振功能。

2 阻尼控制电压计算方法

在控制系统中使用所建立的阻尼力模型时，将减振器运行时每一时刻的状态看作是由对应的正弦激励产生的，然后确定该时刻状态参数在对应的正弦激励中的位置，再由所需的阻尼力和位置参数计算出在该正弦激励下减振器应该产生的最大阻尼力，最后将最大阻尼力和最大速度代入式(1)求出控制电压。

根据测得的减振器实时运行状态参数(位移、速度和加速度)确定该时刻对应的正弦激励的最大振幅和最大速度，其中最大速度由式(2)计算，最大振幅为

(3)

将测得的位移和速度按最大振幅和最大速度归一化为

(4)

(5)

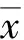
(6)

将计算得到的该时刻对应正弦激励的最大速度和所需最大阻尼力代入式(1)求出控制电压。

3 磁流变半主动悬架控制仿真

2自由度汽车悬架模型包含簧载质量垂向加速度、悬架动挠度和轮胎动载荷这些表征汽车平顺性的主要参数，因此广泛应用于悬架控制策略的研究。将基于所建模型的磁流变减振器控制电压计算方法应用于汽车的磁流变半主动悬架控制系统，通过模糊控制方法来仿真分析悬架的控制效果，验证控制电压计算方法的可行性。

2自由度磁流变半主动悬架的振动方程为

(7)

式中：ms=350kg为簧载质量；mu=41kg为非簧载质量；c=290N·s/m为悬架的机械阻尼；ks=19.5kN/m为悬架的刚度；ku=192kN/m为轮胎的刚度；FMR为磁流变减振器可控阻尼力；q为随机路面输入。

模糊控制器设计为双输入单输出系统，以簧载质量速度和簧载质量与非簧载质量的相对速度作为模糊控制器输入，分别记作v和vr；以理想的悬架控制力作为输出变量，记作u。输入变量采用钟形隶属度函数，设置5个语言变量；输出变量采用三角形隶属度函数，设置7个语言变量；模糊控制规则见表1。模糊逻辑推理方式选择Mamdani方式，解模糊方法采用质心法。

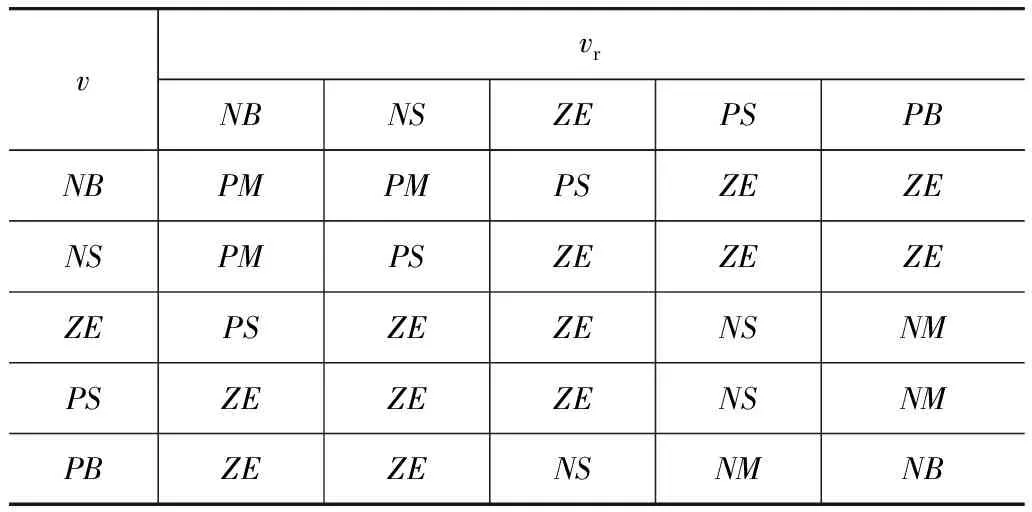
表1 半主动悬架模糊控制规则表

在Matlab/Simulink中建立2自由度磁流变半主动悬架的仿真程序，系统框图如图10所示。将模糊控制器得到的理想控制力导入控制电压计算模块，得到对应的控制电压，然后通过磁流变减振器输出可控的阻尼力。假定车辆以72km/h直线行驶在B级路面上进行仿真，得到在减振器可控阻尼力作用下悬架各性能评价指标的功率谱密度，如图11～图13所示。减振器实际阻尼力与理想控制力对比如图14所示。

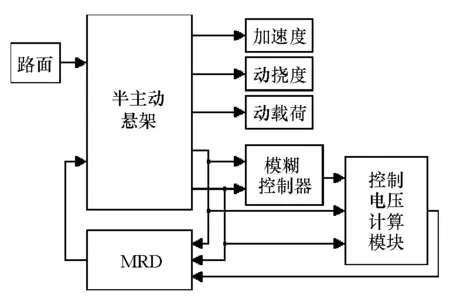
图10 磁流变半主动悬架仿真程序系统框图

图11 簧载质量加速度功率谱密度

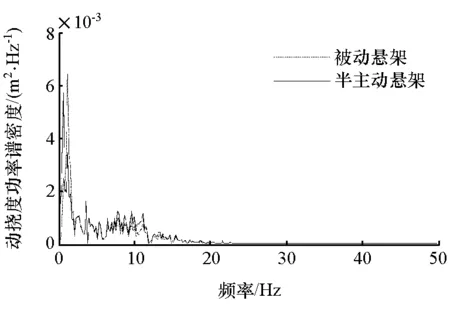
图12 悬架动挠度功率谱密度

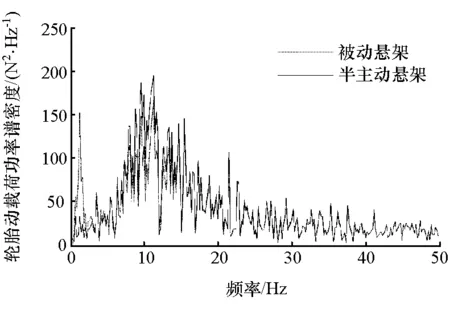
图13 轮胎动载荷功率谱密度

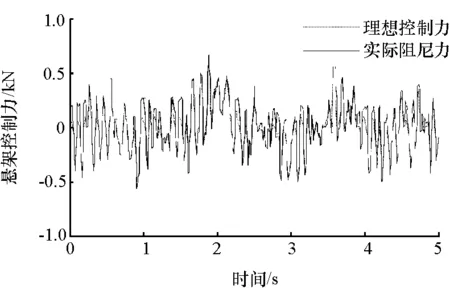
图14 磁流变半主动悬架控制力

悬架性能评价指标的均方根值如表2所示。仿真结果表明，模糊控制的磁流变半主动悬架具有良好的减振性能，特别是在低频阶段；磁流变液减振器的输出阻尼力能够很好地跟随理想的控制力，说明本文中控制电压计算方法是有效的，能够准确地计算出理想阻尼力对应状态下的控制电压。然而在控制力较小时减振器阻尼力与理想控制力间存在误差，这是由于所需的理想控制力小于对应状态下减振器能够输出的最小阻尼力而造成的，整体来看该误差对控制效果影响很小。后续的研究将进行电压实时控制的台架试验与验证。

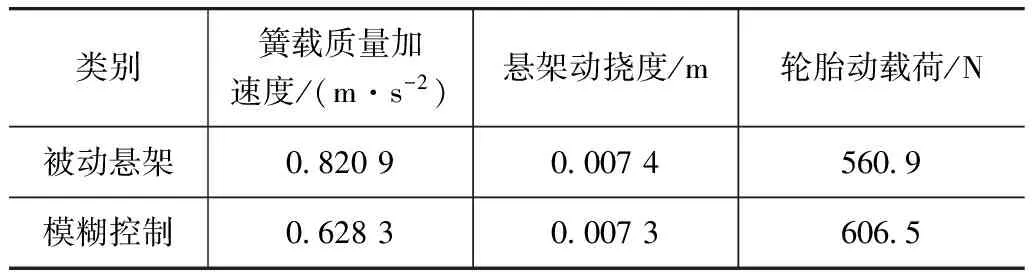
表2 悬架性能评价指标均方根值

4 结论

根据磁流变减振器阻尼特性的试验和分析结果，提出了一种将参数化建模与非参数化建模方法相结合的建模方法，验证结果表明，该方法能很好地模拟磁流变减振器的阻尼特性，且该模型的输入是减振器运动状态参数和电压，因此方便用于实时控制。研究了基于该模型的控制电压计算方法，并将其应用于汽车磁流变半主动悬架的控制仿真，结果表明该控制电压计算方法是有效的，磁流变减振器具有良好的减振性能。

[1] 潘公宇.磁流体阻尼可调减振器[J].机械工程学报,2002,38(7):148-152.

[2] YOKOYAMA M, HEDRICK J K, TOYAMA S. A Model Following Sliding Mode Controller for Semi-active Suspension Systems with MR Dampers[C]. Proceedings of the American Control Conference, Arlington, Virginia,2001:2652-2657.

[3] 李以农,郑玲.基于磁流变减振器的汽车半主动悬架非线性控制方法[J].机械工程学报,2005,41(5):31-37.

[4] 郭大蕾,胡海岩.基于磁流变阻尼器的车辆悬架半主动控制研究——间接自适应控制与实验[J].振动工程学报,2002,15(3):285-289.

[5] 李艳阳,李以农,郑玲,等.基于Takagi-Sugeno模型的磁流变半主动悬架控制[J].系统仿真学报,2013,5(25):1065-1070.

[6] STANWAY R, SPOSTON J L, STEVENS N G. Non-linear Modeling of an Electro-rheological Vibration Damper[J]. Journal of Electrostatics,1987(20):167-184.

[7] 王皖君,应亮,王恩荣.可控磁流变阻尼器滞环模型的比较[J].机械工程学报,2009,45(9):100-108.

[8] SPENCER B F, DYKE S J, SAIN M K, et al. Phenomenological Model for Magnetorheological Dampers[J]. Journal of Engineering Mechanics,1997,123(3):230-238.

[9] SCHULER K C, ROSCHKE P N. Neuro-fuzzy Modeling of a Magnetorheological Damper Using ANFIS[C]. Proceeding of 9th IEEE international Conference on Fuzzy Systems. San Antonio, Texas,2000:122-127.

[10] TRUONG D Q, AHN K K. Identification and Application of Black-box Model for a Self-sensing Damping System Using a Magneto Rheological Fluid Damper[J]. Sensors and Actuators A,2010(161):305-321.

[11] 王戡,郑玲,刘非.基于广义回归神经网络的磁流变减振器模型辨识[J].汽车工程,2013,35(7):619-634.

[12] 杨海.磁流变液减振器建模及磁流变半主动悬架控制研究[D].镇江:江苏大学,2014.

[13] 张泽旭.神经网络控制与Matlab仿真[M].哈尔滨:哈尔滨工业大学出版社,2011.

A Study on the Modeling of Magneto-rheological Damper and theVibration Control of Semi-active Suspension

Pan Gongyu, Houguan Yuanqing & Yang Hai

SchoolofAutomobile&TrafficEngineering,JiangsuUniversity,Zhenjiang212013

A novel damping force model combining parametric model and non-parametric model is proposed based on the test results of magneto-rheological (MR) damping characteristics. The model uses an adaptive neural-fuzzy inference system to simulate the hysteresis characteristics of damping and conducts the numerical fitting on the relationships between damping versus voltage and speed. The results of verification show that the model can well approximate test results and reflect its hysteresis characteristics. On this basis, the calculation method of control voltage in damping model is derived and applied to the simulation on the MR semi-active suspension control of vehicle. The results demonstrate that MR semi-active suspension can better enhance the ride comfort of vehicle and the calculation method proposed of control voltage is feasible and effective.

magneto-rheological damper; modeling; semi-active suspension; vibration control

*国家自然科学基金(51375212)、江苏省汽车工程重点实验室开放基金(QC201304)和江苏省动力机械清洁能源与应用重点实验室开放基金(QK13003)资助。

原稿收到日期为2014年12月24日，修改稿收到日期为2015年7月13日。