一种新型凸轮实验装置设计及分析*

李长勇，巨　刚，袁　亮，刘祖兵，刘小月，王文建

(新疆大学 机械工程学院，乌鲁木齐　830047)



一种新型凸轮实验装置设计及分析*

李长勇，巨刚，袁亮，刘祖兵，刘小月，王文建

(新疆大学 机械工程学院，乌鲁木齐830047)

摘要：为解决传统机械中设计凸轮机构周期长、精确度低、实验研究参数对应关系不直观等客观性问题，设计并制造出了一种新型凸轮实验研究装置。凸轮实验装置在结构设计中使用同步带提高运动精度，线性导轨提高装置的运动稳定性，从而保证了凸轮机构的设计精度。该装置是一种从几何、运动、力学三方面特性来对凸轮研究的实验仪器，采用旋转变换原理和平移变换理论以及运动的合成与分解思想对凸轮轮廓线设计装置及从动件运动规律曲线研究装置进行理论性分析，同时建立了三维有效模型，运用UG运动分析工具箱对两种实验装置进行了实例验证，并且用实际凸轮实验装置在专用实验图纸上设计了凸轮轮廓线，分析了推杆运动规律曲线之间的关系及从动件运动规律曲线的推(回)程、推(回)程运动角、远(近)休止角、冲击点等参数。最后对UG分析和实际凸轮实验装置设计的凸轮及测得数据进行对比，验证得出新型凸轮实验研究装置能够满足要求，具有很高的实用性。

关键词：凸轮实验装置；运动规律曲线；凸轮运动参数

0引言

凸轮机构被广泛应用于我国国防军工、航空航天机械装置领域以及其他轻工业领域中，比如，发动机、纺织、造纸、印刷等行业。随着科技发展，各种复杂类型的凸轮更是大范围得到应用，可随之带来就是复杂凸轮机构的设计问题，如何能短周期内设计出精度更高，稳定性更好的复杂型凸轮？很多学者、研究者一直以来都在努力解决着这个问题。

传统设计凸轮轮廓的方法有作图法和解析法[1-2]，作图法简便、直观、但误差较大、不精确，只适用于低速或不重要场合，不能满足目前凸轮机构高速度和高精度方面要求，现已被解析法取代。解析法虽然作图精确，但是不直观，需要大量时间进行解析计算。 目前，我国研究者、学者研究设计凸轮机构的贡献如：张玉华和辛重镐等[3-4]最新提出适用于各种平面凸轮廓设计的通用方法一相对运动法:基于反转原理的通用模型,利用坐标系和齐次坐标变换技术,由从动件相对凸轮运动的相对速度、相对加速度和从动件的表面法线导出平面凸轮的轮廓方程;罗贤海等[5]采用遗传程序方法对凸轮理论轮廓线进行拟合,对凸轮轮廓进行设计等；在国外许多研究者对凸轮轮廓设计的研究也做了很大贡献，比如：文献[6]用共辘曲面法和等距曲面法用于设计平面凸轮轮廓；文献[7-8]瞬心法(Pofa: methed)、复变量法(complex variable method)求得压力角和曲率半径设计凸轮轮廓等；除此之外还有按最佳加速度设计凸轮廓线、根据残留振动为目标函数设计凸轮轮廓、依照位移的均方根误差为目标函数来控制凸轮轮廓的谐量等方法。

笔者是针对凸轮轮廓设计和从动件运动规律曲线实验综合研究提出来的一种新型设计。能准确地、快速地设计出凸轮轮廓的同时还能对凸轮机构的各运动参数进行研究分析，在理论分析后能在实际制造出的凸轮实验研究装上进行验证，为凸轮研究者提供一种直观地分析和研究凸轮实验的平台，同时对凸轮机构的优化、动态分析提供了实验基础，具有实际的使用价值。

1传动分析

凸轮实验研究装置采用同步带传动，实现整个系统传动速度相等。带与带轮靠啮合传递运动和动力，之间无相对滑动，传动比准确，能充分满足实验装置精度要求及传动需求。如图3所示:

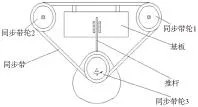
图1　同步带传动机构简图

2三维有效模型分析

2.1建立三维有效模型

运用SolidWorks三维软件建立凸轮实验装置三维模型，如图2、图3所示。

图2凸轮轮廓曲线设计装置是根据已给定的从动件运动规律曲线设计凸轮轮廓曲线；图3从动件规律曲线研究装置是根据给定的凸轮轮廓线研究从动件运动规律曲线，其主要研究的凸轮机构主要参数(推程角、远休止角、回程角、近休止角、推程、冲击点等)。

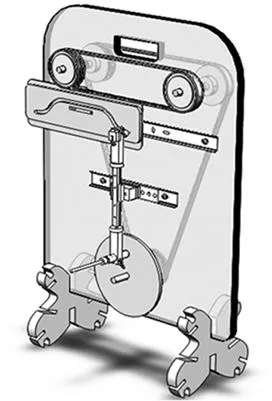
图2　凸轮轮廓曲线设计装置

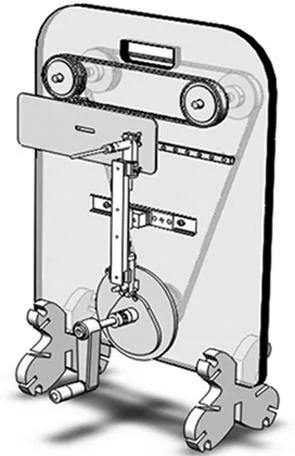
图3　从动件规律曲线研究装置

2.2凸轮轮廓设计简化模型运动特征分析

如图4所示，凸轮实验装置在设计凸轮轮廓时，将从动件运动规律曲线板安装在凸轮实验装置图纸基板上，再将连架杆嵌入从动件运动规律曲线板中，此后通过磁铁将推杆连接于偏心导轨之上(偏置导轨可以调节为对心、偏心)。然后将绘图纸安装在圆形绘图板之上。设计凸轮轮廓时，水平移动从动件运动规律曲线板，驱动推杆以速度为v在竖直方向作直线运动同时带动同步带以ω角速度转动，使圆形绘图板拥有同步带轮的角速度转动，此时记录笔绘制一个周期的两个运动的合成曲线——凸轮理论轮廓线。

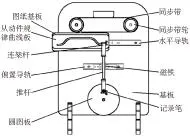
图4　凸轮轮廓设计

为了用理论公式研究凸轮轮廓曲线，将圆图版固定，滚子推杆以角速度-ω转动一定的角度，如图5所示,凸轮机构上建立直角坐标系Oxy,原点O位于凸轮回转中心，当从动件在1位置时，滚子中心B0点为凸轮推程理论廓线起始点，当整个凸轮机构反转β角后，从动件达到2位置，B0点到达B1点，此时从动件位移为S0=BB1。由图6可以看出，从动件B1运动可以看作是由B0反转β后到达基圆B点再沿导路移动位移S0到达B1点，设B0点坐标为(xB0,yB0),B1点坐标为(x,y)，应用旋转变换和平移变换求得B1的坐标为：

(1)

式中，xB0=0,yB0=S=R，sx=S0sinβ,sy=S0cosβ

求得：

(2)

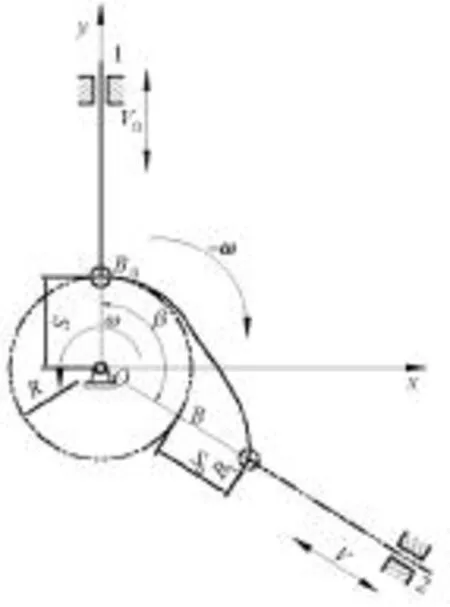
图5　凸轮的理论轮廓线图

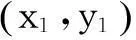
(3)

其中θ为公法线与x轴的夹角，(x,y)为滚子圆心(位于理论廓线上)的坐标。

(4)

对式(2)求导可得：

(5)

综合式(3)、(4)可得：

(6)

将(6)代入到(3)中即可求得凸轮实际廓线方程。以等加速等减速为例子，凸轮实际廓线方程为：

(7)

说明：笔者中的凸轮轮廓研究设计装置就是根据以上(几何分解与合成)原理来设计的，由于针对的凸轮轮廓不同求出来的轮廓线方程复杂程度有所差异，以上理论可以求解等减速等减速、正弦、余弦、高次多项式等凸轮。涉及到版面篇幅问题，不再一一推导。

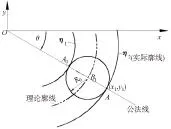
图6　凸轮的实际轮廓线

2.3从动件运动规律曲线研究简化模型运动特征分析

凸轮实验装置在研究从动件运动规律曲线，由给定的等加速等减速凸轮外廓绘制从动件运动规律曲线。如图7所示，手柄带动凸轮绕基圆圆心转动，凸轮推动圆柱滚子推杆在竖直方向上下运动，同时同步带也随着手柄转动，带动方图板水平运动，推杆上的绘图笔在方图板绘制出从动件运动规律曲线。对应关系如下图8所示。

图7　从动件运动规律曲线绘制

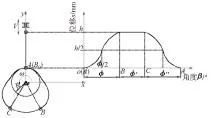
图8　推杆位移变化规律

如图8所示凸轮廓线由AB、BC及CA三部分组成。当滚子推杆与A点接触时，此时推杆处于最低位置。移动运动规律曲线板使同步带带动凸轮沿逆时针反向转动，滚子推杆在凸轮廓线AB段的推动下，将由最低位置A被推到最高位置B,推杆的这一过程即为推程，则相应的凸轮转角∠AOB为推程运动角。当推杆与凸轮廓线的BC段接触时，由于BC段为以凸轮轴心O为圆心的圆弧，所以滚子推杆将处于最高位置而静止不动，这一过程即为远休止，则与之相对应凸轮转角∠BOC为远休止角。同理，当推杆与凸轮廓线的CA段接触时，推杆将由最高位置被推到最低位置,推杆的这一过程即为回程，近休止角为0。

如图9、图10所示描述了等加速等减速运动规律过程，由图可见，其在a、b、c、c′、d、e六点的加速度有突变，不过这一突变为有限值，因而引起的冲击较小为柔性冲击。在绘制滚子推杆的运动表达式的过程中，通过对推杆的运动规律进行分析(即推杆的位移s、速度v和加速度a随角度β变化的规律)，可以判断推杆运动时有无冲击点以及冲击点的位置。

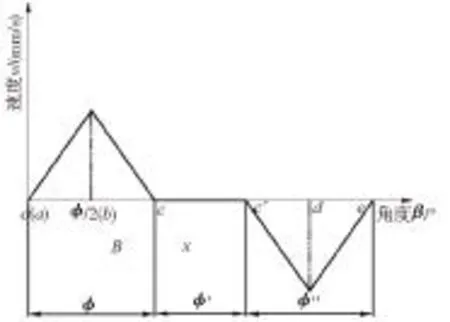
图9　推杆速度变化规律

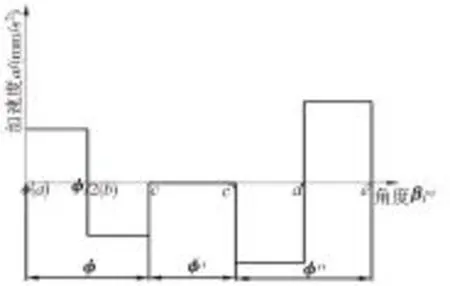
图10　推杆加速度变化规律

3仿真试验与实际测量数据分析

3.1应用UG对凸轮实验装置仿真分析

3.1.1设计凸轮轮廓线

以从动件等速运动规律曲线设计凸轮轮廓为例进行仿真分析。

等速运动规律条件：(推程)h=31mm,(远休止角)Φ′=60°,(推程)Φ=153°，(回程)Φ″=147°(无近休止角)。

仿真分析中，是以运动规律曲线板为恒定驱动，通过连架杆推动推杆上下运动，圆图板随同步带轮转动，推杆上下运动和圆图板的转动合成凸轮外廓，并通过记录笔绘制出图形。如图11所示是推杆位移随时间变化曲线和给定的运动规律曲线完全一致，仿真结果表明运动没有削减。如图12所示是推杆速度随时间变化曲线，1段曲线和3段曲线表明速度相等，2段曲线表明速度为0，再次证明了其为等速运动规律曲线。如图13所示是推杆加速度随时间变化曲线，1段和2段曲线相同，并且刚好处于由推程段向远休止段转换时，远休止段再向回程段转换的时期，加速度发生了突变，也是冲击形成的原因。综合分析表明符合等速运动规律曲线。如图14所示是UG仿真的等速凸轮轮廓线形成的最终结果。图15是由图2凸轮设计实验装置设计的凸轮实际轮廓线。

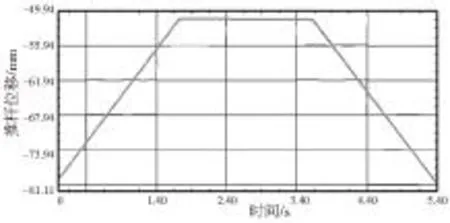
图11　推杆位移随时间变化曲线

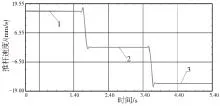
图12　推杆速度随时间变化曲线

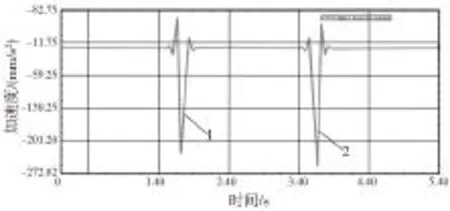
图13　推杆加速度随时间变化曲线图

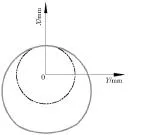
图14　设计等速凸轮轮廓线

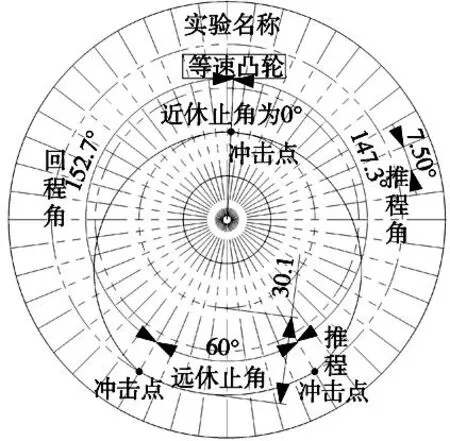
图15　实际中设计出的等速凸轮轮廓线

总结：图15是为该凸轮实验装置设计的专门实验图纸，它由间隔为7.5°的射线和同心的圆构成。在由已知推杆运动规律反向设计凸轮廓线过程中，从极坐标中可以清晰的表示出基圆大小和推(回)程、推(回)程运动角、远(近)休止角、冲击点等凸轮机构主要运动参数。

理论给的条件相比实际中测得推程、推程角、回程角、远休止角的数据误差约为2‰~6‰，符合实验装置设计精度，也充分说明了凸轮轮廓曲线设计装置能进行精确凸轮轮廓设计。

3.1.2从动件运动规律曲线绘制实验

等速运动规律条件：(推程)h=30mm,(远休止角)Φ′=88°,(推程)Φ=136°，(回程)Φ″=136°(无近休止角)。

以等速度等凸轮运动为例进行仿真分析如下图所示:

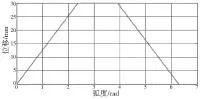
图16　位移随弧度变化曲线

图17　速度随弧度变化曲线

图18　加速度随时间变化曲线

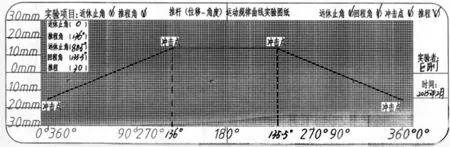
图19　实际中设计出的等速运动规律曲线

UG对凸轮实验装置仿真过程中，以手柄为恒定驱动设置角速度为36°/s匀速转动，设置时间为10s,计算步数为360步，即凸轮每转1°时模型的运转情况。由图16位移随时间变化曲线、图17速度随时间变化曲线、图18加速度随时间变化曲线，图19是由图3运动规律曲线研究实验装置绘制出来的规律曲线。

位移曲线绘制实验纸如图19所示，它由横向和纵向的直线垂直相交构成，每一小格长度为1mm的正方形，构成许多直角坐标系，横坐标每个方格为1.8°。根据凸轮绘制推杆运动规律的曲线时，能够标识出推程、冲击点等参数，并可以分析出速度、加速度随角度的变化规律，方便研究凸轮廓线组成部分与推杆运动规律曲线之间的对应关系。

理论用UG软件仿真分析的数据和运动规律曲线研究实验装置测量出来的数据吻合，验证了凸轮研究实验装置的实用创新性。

4结论

(1)凸轮实验研究装置是一种新型的设计为凸轮机构研究提供了一个崭新的平台。

(2)用SolidWork对凸轮实验装置的两个实验装置进行三维建模，用简化模型对运动特征进行了详细分析。

(3)用UG软件对各个状态进行了仿真实验，并对每个实验结果进行了详细分析，得到的结果和专门的实验专用纸实际测量的结果基本相符合，能够满足精度要求。实验表明，能快捷设计凸轮轮廓曲线和精确绘制从动件运动规律曲线。

[参考文献]

[1] 孙桓,陈作模,葛文杰.机械原理[M].北京:高等教育出版社,2006.

[2] 濮良贵,纪名刚.机械设计[M].8版.北京:高等教育出版社,2006.

[3] 张玉华，须知让，包家汉,等.确定盘行凸轮曲率半径的相对加速法及其应用[J].安徽工业大学学报，2003,20(4):303-307.

[4] 张玉华，辛重镐.设计平面凸轮轮廓的新方法[J].机械工程学报，2004,40(1):33-37.

[5] 罗贤海，翁海珊，张曦.基于遗传程序的凸轮轮廓曲线设计[J].机械设计与制造,2008(10):22-24.

[6] Tsay D M,Wei H M.A general approach to determination of planar and spatial camprofiles[J]. ASME Journal of Mechanical Design, 2006,118(1):256-265.

[7] Fan Y Chen.Mechanies and Design of Cam Mechanisms[M].New York: Pergamon Press Inc,1992.

[8] Shin J H , Lee C M, Kim J S.Shape design of disk cam mechanisms using instant velocity centers[C].IN:Proceeding of 6thinternational symposium on TransPort Phenomena and Dynamics of Rotating Machinery,1996:178-186.

[9] 宋晓华，方坤利.基于UG凸轮机构设计和运动仿真[J].机械研究与应用，2005,18(1):102-103.

[10] Bagci C，Kurnool S．Exact response analysis and dynamic design of cam-follower systems using Laplace transforms[J].ASME Journal of Mechanical Design，1997，119(4):359-369.

[11] 郭磊,褚超美，陈家琪，高次多项式凸轮线性特性参数对汽配机构性能影响的研究[J],内燃机工程,2005,26(1):21-23.

[12] 宋晓华，方坤利.基于UG凸轮机构设计和运动仿真[J].机械研究与应用，2005,18(1):102-103.

(编辑李秀敏)

Design and Analysis of a New Experimental Device of Cam

LI Chang-yong,JU Gang,YUANG Liang,LIU ZU-bing,LIU Xiao-yue,WANG Wen-jian

(School of Mechanical Engineering, Xinjiang University, Urumqi 830047,China)

Abstract：In order to solve the subjective problems in cam design of traditional mechanic such as long period, low precision, non-intuitive corresponding relation in test and research parameter, it designs and produces one kind of new cam test and research equipment. Cam test equipment uses hold-in range to enhance movement precision in the mechanism design, and linear rail to enhance movement stability of equipment, so that it guarantees design precision of cam mechanism of equipment. This equipment is one kind of test equipment of using 3 aspects such as geometry, movement and mechanics to make research on cam, it adopts rotated and converted principle as well as translation theory and synthesis and decomposition of movement to make theoretical analysis on design equipment of cam outline and movement discipline of follower to make test demonstration, at the same time establishes 3-D effective model, using UG movement analysis tool to make test demonstration on 2 kinds of test equipment, and it uses practical cam test equipment to design cam outline in the expert test drawings, makes analysis on relations between curves of putter movement discipline and pull(push)distance, pull(push)distance angle, discipline of follower movement curve, remote(near) angle of repose, impact point etc. Finally, it makes comparison on UG analysis and cam designed by practical test equipment as well as test data, and gets the new cam test and research equipment by demonstration can meet requirement and has high practicability.

Key words：cam experimental device ；curves of putter movement discipline ;cam motion parameters

中图分类号：TH132；TG65

文献标识码：A

作者简介：李长勇(1976—)，男，乌鲁木齐人，新疆大学讲师，博士，研究方向为机器人研究；通讯作者：袁亮(1972—)，男，乌鲁木齐人，新疆大学教授，硕士生导师，博士，研究方向为机械电子、机器人、无人机,(E-mail)123514045@qq.com。

*基金项目：国家自然科学基金资助项目(61262059, 31460248)；新疆优秀青年科技创新人才培养项目(2013721016)；新疆大学博士启动基金、自治区科技支疆项目(201591102)

收稿日期：2015-05-06；修回日期：2015-06-06

文章编号：1001-2265(2016)03-0123-05

DOI:10.13462/j.cnki.mmtamt.2016.03.034