考虑支撑变形的转盘轴承接触载荷分布的计算*

毛范海，张　建，董惠敏，孙振生，王德伦

(1.大连理工大学 机械工程学院，辽宁 大连　116024；2.瓦房店轴承集团有限责任公司，辽宁 瓦房店　116300)



考虑支撑变形的转盘轴承接触载荷分布的计算*

毛范海1，张建1，董惠敏1，孙振生2，王德伦1

(1.大连理工大学 机械工程学院，辽宁 大连116024；2.瓦房店轴承集团有限责任公司，辽宁 瓦房店116300)

摘要：提出一种考虑轴承套圈及其支撑结构弹性变形的大型转盘轴承接触载荷分布的计算方法。利用该方法分析了支撑结构弹性变形、轴承游隙及初始接触角对四点角接触球轴承接触载荷及接触角分布的影响。其结果与采用有限元方法得到的结果基本吻合，且计算效率大大提高。研究成果为定性分析大型转盘轴承的承载能力提供了理论依据。

关键词：转盘轴承；柔性支撑；接触载荷

0引言

大型转盘轴承是起重机械、工程机械、风力发电等领域中的重要部件，这种轴承与普通标准轴承有很大区别—套圈直径一般很大，通常是钢球直径的几十倍，而且转盘轴承可以承受很大的倾覆力矩。在很大的外载荷下，由于支撑结构的柔性导致套圈的变形不可以忽略，而套圈的变形对钢球与沟道之间的接触载荷有很大的影响，所以在设计计算转盘轴承时，需要一种考虑到支撑刚度的更精确并且快速的方法，计算轴承的接触载荷分布，为转盘轴承的设计计算提供参考。

文献[1-2]假设轴承套圈是完全刚性的，只有钢球与沟道接触处有局部的弹性变形，在赫兹点接触理论的基础上，建立了四点角接触球轴承在任意联合外载荷作用下接触载荷分布的5自由度数学模型。文献[3-4]提出了类似的分析模型。使用有限元分析方法，建立轴承的三维有限元模型[5-7]，可以得到较为精确的结果。然而对轴承进行有限元分析，需要建立大量接触对，包括钢球与沟道以及螺栓与轴承套圈的接触。由于钢球与沟道之间的接触区域很小，为了真实反映接触应力梯度，就需要对接触区域划分非常小的网格，造成计算时间长、收敛困难的问题。文献[4]通过理论分析模型得到最大的接触载荷，建立一个钢球与沟道的扇形区域的三维有限元模型，计算接触区表面及接触区以下的应力。文献[7-10]在有限元模型中，使用非线性弹簧或杆单元等效钢球与沟道的接触，大大降低了计算量，但这种等效方法的正确性还有待验证。

本文以单排四点角接触球轴承为例，建立包含支撑结构刚度的轴承静力学分析模型(下文称之为弹性分析模型)，且考虑由于支撑结构刚度分布不均所引起的轴承接触载荷及接触角分布的变化，而且计算效率较高；建立钢球-沟道精确接触有限元模型，对轴承进行有限元分析，验证弹性分析模型的正确性；分析轴承游隙及初始接触角对此类轴承承载能力的影响。

1弹性分析模型静力学建模及求解

1.1模型假设

将轴承内、外套圈等分为n段(n取大于零的整数)，相邻两段之间有一段很小的套圈连接段，如图1所示。为简化模型，做如下假设：

(1)假设套圈的每一段为完全刚性，称之为刚性段，按照刚性套圈假设[1-2,4]，钢球与沟道之间的接触满足赫兹接触理论的适用条件；刚性段只有在沟道与钢球接触的局部位置发生弹性变形，每个刚性段有五个自由度，即三个平动自由度和两个转动自由度；轴承套圈与支撑结构在结合面完全粘合。

(2)轴承套圈在非接触区域的变形都集中在套圈连接段，即每一个套圈连接段可以看作一个具有两节点的三向拉压及两向扭转刚度的弹簧。此弹簧的刚度包含了弹簧位置原套圈的刚度及与套圈连接的支撑结构的刚度。

图1　模型假设

1.2接触变形协调

参考文献[4]的方法，对套圈的某一刚性段进行分析，如图2所示。内、外圈沟道曲率中心记为：Ciu,Cil,Ceu,Cel,下标i及e分别表示内圈和外圈，下标u和l分别代表上沟道和下沟道。全局坐标系原点取在轴承节圆中心，z轴方向为轴向方向。轴承受载前，内外圈刚性段中心Oi及Oe重合，各个沟道曲率中心位置为]span。

图2　套圈刚性段变形协调

在受载后，设内外圈刚性段中心分别发生微小位移δi及δe，则内外圈刚性段中心相对位移为：

δ=δi-δe

(1)

r′=Tr+δr

(2)

其中：

当θ和γ很小时，

(3)

‖CiuCel‖及‖CilCeu‖分别是内圈上沟道曲率中心与外圈下沟道曲率中心之间的距离及内圈下沟道曲率中心与外圈上沟道曲率中心之间的距离，本文简称为沟心距Δ，轴承受载后其大小为：

(4)

将Δiu-el及Δil-eu向径向平面投影得到有效的沟心距‖(Δiu-el)r‖、‖(Δil-eu)r‖。钢球角位置φ处径向平面的单位法向量为：

(5)

则

(6)

其中：S(n)=I-nnT，I为单位矩阵。

在载荷作用前，沟心距：

(7)

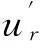
沟心距的变化即为被钢球隔开的内外两个沟道之间的法向趋近量，其大小为：

(8)

如果弹性趋近量δ>0，说明钢球与沟道发生接触，否则没有发生接触。

根据赫兹点接触理论，钢球与沟道之间的接触力Q与两个沟道之间的法向趋近量δ满足关系：

(9)

使用单位向量表示接触力的方向，表示为：

(10)

对于内圈取正号，对于外圈取负号。

1.3平衡方程

如图3，对于外圈每个刚性段，接触力与支反力平衡，并将支反力转化到套圈中心，得到平衡方程[4]：

(11)

图3　受力分析

对外圈结构(轴承外套圈及与其连接的结构)整体进行分析，其自由度包含外圈各刚性段圆心的自由度δer和支撑结构上载荷节点的自由度δep，满足平衡方程：

(12)

在有限元软件ANSYS中建立包含支撑的外圈结构的有限元模型，其中单元类型选择8节点六面体单元solid185，弹性模量及泊松比根据实际情况选取。根据刚度矩阵的定义，计算得到外圈结构的刚度矩阵Ke:

同理得到内圈结构的平衡方程：

(13)

内圈或外圈第k个刚性段的节点力为：

(14)

Fsegm,k、Msegm,k的计算如式(11)。

联立式(12)、(13)、(14)并引入边界条件，得到总体平衡方程：

(15)

1.4模型数值求解

方程(15)为非线性方程组，自由度

Dof=10n+6m

其中，n为套圈分段数，m为载荷节点数。本例中n=16，m=2。

使用Levenberg-Marquardt优化方法求解。这种方法相比Gauss-Newton算法在迭代过程中不需要雅各比矩阵列满秩，所以这种方法应用更广泛。

使用matlab编写求解程序，轴承结构参数、载荷参数、分段数、内、外圈结构刚度矩阵作为输入，各刚性段节点及载荷节点的位移为待求解未知量，初值取为0-1的随机数列。

2有限元模型

2.1网格划分

使用有限元方法分析回转轴承的承载能力，需要建立大量接触对，并且接触区域的网格质量要足够好。为了真实反映钢球与沟道在接触处的曲率半径，需要对其划分很小的单元尺寸，一般单元划分尺寸控制在接触椭圆半轴的0.2倍。为了减少节点数的同时保证较好的网格质量，采用在接触区域重新划分网格的方法，如图4所示。

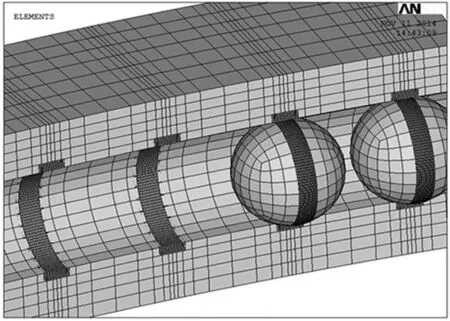
图4　钢球-沟道接触区细化单元

有限元模型中单元类型选择solid185，材料参数见表1。

表1　有限元模型材料参数

2.2边界条件

载荷施加位置如图5所示。塔筒下端面全约束；将轴承内外圈分别与塔筒及机舱固联；约束外圈及钢球绕z轴的周向转动；钢球与沟道之间建立柔性接触，摩擦系数设置为零。

图5　有限元模型边界条件

3算例及结果分析

以4MW风电偏航轴承(见图5)为例，对轴承的接触载荷分布及接触角分布进行研究。轴承的载荷工况、结构参数见表2、表3。

表2　偏航轴承极限载荷工况

表3　轴承结构参数

结合给定算例,分别使用弹性分析模型、有限元模型以及完全刚性套圈模型[4]对轴承接触载荷等进行分析。

为进行对比分析，对三种模型的其他条件做统一处理：

(1)为获得弹性模型中的刚度矩阵而建立的有限元模型，其结构及材料参数同精确接触有限元模型；

(2)弹性分析模型与精确接触有限元模型具有相同的外载荷条件及约束条件；

(3)按照理论力学方法将作用在机舱的外载荷转化到套圈中心，将转化后的载荷作为完全刚性套圈模型的外载荷。

3.1计算结果对比与分析

图6、图7分别为三种模型计算得到的接触载荷及接触角分布。从图中可以看出，使用弹性分析模型和有限元模型得到的结果基本吻合。还可以看出，弹性分析模型载荷分布在刚性段连接处发生突变。引起这种突变的原因是由于相邻两刚性段在连接处发生较大相对位移所致。

使用三种模型计算得到的最大接触力、最大接触角及计算时长列于表4。可以看出，相对于完全刚性套圈模型，弹性分析模型及有限元模型的结果比较保守。

从计算时长来看，弹性分析模型及完全刚性套圈模型的计算效率远高于有限元模型。因此，当对于计算精度要求不高且要进行循环计算时，使用完全刚性套圈模型及本文所建立的弹性分析模型比较合适。

图6　接触载荷分布

图7　接触角分布

计算模型弹性分析模型有限元模型完全刚性套圈模型最大接触力/kN157.0139.8124.6最大接触角/°(初始接触角45°)57.861.553.4计算时长12s32h2.1s

3.2支撑结构变形对接触载荷的影响

力矩载荷作用位置不同，支撑结构及轴承套圈的弹性变形就会发生变化，因此，本文通过改变外载荷My的作用位置分析支撑结构变形对接触载荷的影响，作用位置由图5的节点2位置移至节点1位置，外载荷作用点改变后的结果如图8、图9。可以看出，改变力矩载荷作用位置后，接触力和接触角分布更均匀，这是由于当力矩载荷作用在节点1时，支撑结构变形更均匀所导致。

图8　支撑结构变形对接触载荷分布影响

图9　支撑结构变形对接触角分布影响

改变力矩载荷作用位置后所得到的最大接触力、最大接触角列于表5。可以看出，支撑结构的弹性变形对轴承的接触力及接触角有很大影响，其对接触力影响更为显著。

表5　改变力矩载荷作用位置后的计算结果

3.3轴承游隙及初始接触角对接触载荷的影响

游隙及初始接触角是轴承的重要结构参数。大型四点接触球轴承一般取小游隙或负游隙，以减小冲击振动。初始接触角越大，轴承的轴向承载能力越大，能承受的倾覆力矩就越大，但轴承初始接触角选择过大，会导致轴承受载后钢球与沟道的接触椭圆区域偏至沟道边缘甚至超出沟道圆弧面，出现沟道边缘应力集中现象。

图10、图11分别给出了不同初始接触角下，轴承受载后最大接触力及最大接触角与轴向游隙的关系。可以看出，当游隙在-0.05~0.1mm时，接触力较小且变化较小；但当游隙从-0.05~0.1变化时，接触角急剧增大。综合考虑接触力及接触角因素，此例轴承游隙选取-0.05~0.02mm为优。

图10　不同游隙及初始接触角下的最大接触力

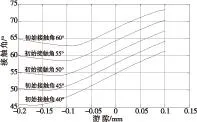
图11　不同游隙及初始接触角下的最大接触角

从图11中还可以看出，当负游隙较大时，初始接触角越大，接触力越大；当游隙绝对值较小时，初始接触角越大，接触力越小。从接触力角度看，在游隙较小的前提下，应该选择较大的初始接触角，但应保证轴承受载后接触角不能过大。

4结论

(1)以四点角接触球轴承为例，建立了包含支撑结构及轴承套圈刚度矩阵的大型转盘轴承静力学模型；建立了精确钢球-沟道接触有限元模型。

(2)采用本文建立的弹性分析模型进行分析可以发现，轴承游隙及初始接触角对轴承受载后的接触力及接触角影响显著；选取绝对值较小的负游隙、较大的初始接触角可提高轴承的承载能力。

(3)采用本文建立的弹性分析模型及有限元模型进行分析得到的结果均表明，大型转盘轴承在较大倾覆力矩作用下，支撑结构及轴承套圈的弹性变形对轴承接触力及接触角分布有显著影响。

(4)由于载荷作用位置直接影响支撑结构的弹性变形，进而影响轴承的接触载荷，因此，在精确计算转盘轴承接触载荷时，需准确确定外载荷的施加位置。

(5)使用本文建立的弹性分析模型所得结果与有限元模型结果基本吻合，且计算效率大大提高，为大型转盘轴承的结构设计提供了理论研究依据。

[1] Zupan S, Prebil I. Carrying angle and carrying capacity of a large single row ball bearing as a function of geometry parameters of the rolling contact and the supporting structure stiffness[J]. Mechanism and Machine Theory,2001, 36: 1087-1103.

[2] Amasorrain J I, Sagartzazu X, Damian J. Load distribution in a four contact-point slewing bearing[J]. Mechanism and Machine Theory,2003, 38: 479-496.

[5] 朱亮，李言. 材料特性对风电轴承耐久性的影响[J]. 西安理工大学学报,2009(04): 460-465.

[6] Olave M, Sagartzazu X, Damian J, et al. Design of Four Contact-Point Slewing Bearing With a New Load Distribution Procedure to Account for Structural Stiffness[J]. Journal of Mechanical Design,2010, 132(2): 021006.

[7] Kania L. Modelling of rollers in calculation of slewing bearing with the use of finite elements[J]. Mechanism and Machine Theory,2006, 41: 1359-1376.

[8] Smolnicki T, Derlukiewicz D, Stanco M. Evaluation of load distribution in the superstructure rotation joint of single-bucket caterpillar excavators[J]. Automation in Construction,2008, 17: 218-223.

[9] Daidié A, Chaib Z, Ghosn A. 3D Simplified Finite Elements Analysis of Load and Contact Angle in a Slewing Ball Bearing[J]. Journal of Mechanical Design,2008, 130(8): 082601.

[10] 尚振国，董惠敏，毛范海，等. 具有塑性变形的转盘轴承有限元分析方法[J]. 农业工程学报,2011，27(12): 52-56.

(编辑李秀敏)

Computational Model for Calculation of Load Distribution of Slewing Bearing Accounting for Structure Stiffness

MAO Fan-hai1,ZHANG Jian1,DONG Hui-min1,SUN Zhen-sheng2,WANG De-lun1

(1.School of Mechanical Engineering,Dalian University of Technology,Dalian Liaoning 116024,China；2.Wafangdian Bearing Co., Ltd.,Wafangdian Liaoning 116300,China)

Abstract：A new computation method is proposed for determining the load distribution in the rolling elements of a large slewing bearing accounting for the flexibility of the bearing ring and its supporting structures. The analysis of the effect of the elasticity of supporting structures, internal clearance and nominal carrying angle on the magnitudes of contact force and actual carrying angle of a four-point contact ball bearing is presented using the method, the results of which have been basically correlated with the results of FE method, and especially the computation efficiency is improved substantially. The above results provide theoretical basis for analyzing qualitatively the static capacity and fatigue lifetime of large slewing bearings.

Key words：slewing bearings; elastic supporting structure; contact force

中图分类号：TH133.3；TG506

文献标识码：A

作者简介：毛范海(1964—)，男，山东宁阳县人，大连理工大学副教授，博士，研究方向为轴承数字化设计，(E-mail)mao_fh@126.com。

*基金项目：辽宁省科技创新重大专项(201303006)

收稿日期：2015-04-29；修回日期：2015-05-20

文章编号：1001-2265(2016)03-0020-05

DOI:10.13462/j.cnki.mmtamt.2016.03.006