基于高斯过程二元分类的刀具切削状态的识别

林景栋，游佳川，黄立沛，刘　欢

(重庆大学 自动化学院，重庆　400044)



基于高斯过程二元分类的刀具切削状态的识别

林景栋，游佳川，黄立沛，刘欢

(重庆大学 自动化学院，重庆400044)

摘要：通过以热室圆盘锯床切削工艺为背景，针对热室圆盘锯床在无法安装测量传感器的情况下需对切削状态进行检测识别的问题进行了研究。通过结合热室圆盘锯床结构特征，选取伺服电机转矩、切削深度和实时切削速度作为状态识别辅助变量，在分析了高斯过程二元分类方法和锯床工艺的基础上设计了一种基于高斯过程分类的切削状态识别器，通过样本数据进行训练后，对热室圆盘锯床的切削状态进行了分类和识别。将识别结果与实际切削状态进行比较，结果表明，高斯过程二元分类的刀具切削状态识别方法能够对热室圆盘锯床工作过程中的切削状态进行有效识别，准确度较高，能够很好的反应热室圆盘锯床切削的实际状态。

关键词：高斯过程；二元分类；切削状态；状态识别

0引言

在热室圆盘锯床的切削工艺中，热室圆盘锯床的主要功能就是在自动化控制系统下对两钢制工件的焊接疤痕通过刀具进行自动打磨切削。在切削过程中，保证切削面的表面光洁度、切割温度和切削精度是热室圆盘锯床切削的一个重要工艺指标，这就要求在切削过程中，控制系统能够根据刀具不同的切削状态实时的更新切削工艺参数。近年来，对刀具切削状态识别的研究虽有了长足的发展[1-6]，然而对于热室圆盘锯床切削工艺而言，由于其切削工件具有较强的放射性且切削环境较为特殊，锯床设备无法安装力传感器、温度传感器、声学传感器等信号采集装置；同时，切削加工伴随着材料和工具的形变及热传导，加工过程具有极强的复杂性和随机性，除此之外，工件的加工过程还存在着加工余量不一致，加工材质不均匀，刀具不断磨损等各种相互耦合和制约的因素，常用的状态识别方法很难适应这样的工况[7]。因此，在实际生产中很难准确的检测识别出当前工况条件下的切削状态，切削工艺参数一般都是加工技术人员凭借经验和参考手册来选取，这就致使加工工艺一致性降低，加工精度下降和加工故障增多。而当加工对象、加工要求、机床条件改变时，仅靠加工人员经验和手册选取工艺参数就更难适应这些变化。因而实现切削过程中切削状态的识别对提高热室圆盘锯床的切削效率、精度、可靠性以及对自动化切削的优化都有着重要意义。

为了解决热室圆盘锯床切削状态的识别问题，本文结合热室圆盘锯床切削工艺和结构特点，从伺服电机反馈信号中抽取切割轴转矩、切削速度、切削深度作为状态识别器的辅助变量，采用高斯过程二元分类方法(GPC)结合进行状态概率预测，大幅提高了切削过程中切削状态识别的准确性，最终实现对热室圆盘锯床切削过程中切削状态的有效识别。

1热室圆盘锯床切削状态识别器

1.1高斯过程二元分类学习模型

高斯过程二元分类模型是建立在高斯过程机器学习基础上的，与高斯过程分类不同的是，高斯过程二元分类模型的主要功能是预测测试数据对应的类别[8-10]。

在高斯过程二元分类模型中，训练数据集可表示为：

D={(xi,yi)|i=1,…,m}

(1)

式中，xi为输入值；yi∈(-1,1)为与之对应的二元分类标志。

通过式可知，高斯过程二元分类模型的主要功能就是预测测试数据x对应的类别y。对于确定的x，其概率密度分布可表示为p(y|x)，满足伯努利分布，设y=1的概率为：

p(y=1|x)=Φ(f(x))

(2)

式中，f(x)称为潜在函数；Φ(·)为标准高斯分布的累计概率密度函数，作用是将潜在函数f(x)的值转换到固定的区间内；在此基础上，进一步选取sigmoid函数Φ(z)=1/(1+e-z)将区间约束的值映射到[0,1]区间。为简化公式表达并方便推导，设fi=f(xi),f=[f1,…,fm]T,X=[x1,…,xm]T。

对于指定的潜在函数，观察值是独立的伯努利分布变量，其似然函数为：

(3)

潜在函数的先验分布为：

p(f|X,θ)=N(0,K)

(4)

式中，K为m×m阶协方差矩阵，Kij=k(xi,xj,θ)，k(·)表示与θ有关的正定协方差函数，θ称为超参数。

高斯过程模型的协方差函数需要满足：对任一点集都能保证产生一个非负正定协方差矩阵。常用的协方差函数为Squared Exponential函数，可表示为：

(5)

式中，超参数θ={σf,l}，最优超参数可通过潜在函数f的极大似然法来估计。

通过不断获得实验观察值，根据贝叶斯规则，潜在函数f的后验分布可表示为：

(6)

1.2高斯过程二元分类预测模型

高斯过程二元分类预测模型主要用于高斯过程分类器的预测过程。由建立的高斯二元分类的学习模型可知，与x*对应的潜在函数值f*的条件概率为：

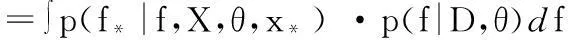
(7)

进一步，y*的预测概率可表示为:

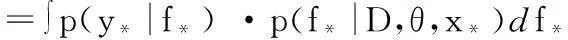
(8)

式中，当y*的预测概率大于0.5时，y*=1，否则y*=-1；由于式(7)和式(8)均无解析解，因此可以采用Laplace’s 与Expectation Propagation 等逼近法获得近似解。设m和A为近似解的均值和方差，则潜在函数f后验分布的近似高斯分布可表示为：

p(f|D,θ)≈q(f|D,θ)=N(m,A)

(9)

同样，f*的后验分布可设为近似的高斯分布，表示为：

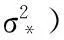
(10)

其中，均值和方差分别表示为：

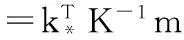
(11)

式中，k*=[k(x1,x2),…,k(xm,x*)]T，表示x*与训练输入X之间的先验协方差矢量。

最后，x*属于第1类的预测概率可表示为：

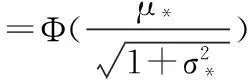
(12)

1.3切削过程辅助变量选取

切削过程中状态的改变，主要是由于切割片自身的磨损造成的。从微观角度来看，随着切削的不断进行，切割片上的切削粒与工件不断摩擦，在完成对工件切削的同时自身也存在着一定磨损，从而导致切削前角变大或者变小[11-12]。因此，在切削速度不改变的情况下，切削力会相应的产生变化。而根据热室圆盘锯床的结构特征，在没有安装额外传感器的情况下，切削力的变化通过传动结构传递反馈，最终反应为伺服电机工作状态的变化。

根据热室圆盘锯床的切削流程，选取切割轴转矩、切削速度、切削深度作为状态识别器的辅助变量。从热室圆盘锯床结构图中可以看出，如图1和图2所示，热室圆盘锯床的切削速度主要是Y轴的进给速度和切割片转动速度的合成；切削深度是X轴上的速度与时间的积分，即切削在X轴上的轴向位移；切割转矩可直接通过伺服驱动器读出。因此，选取的辅助变量可通过伺服驱动器中可读实时参数运算得到。

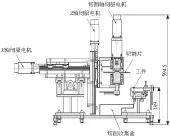
图1　热室圆盘锯床的正视图

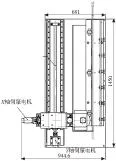
图2　热室圆盘锯床的俯视图

1.4切削过程辅助变量预处理

由于选取的三个辅助变量不在同一量纲，数值各不相同，数量级差别较大，为了不使某个训练样本分量因为过大或过小而使其他的样本分量失去调整意义，需要对训练数据进行归一化处理。通过采用较为常用的Z-Score归一化方法，将所有的辅助变量规范成标准的正态分布，样本数据均转换为无量纲指标测评值，各测评值都处于同一个数量级别上，为后续综合测评分析提供可能。

采用Z-Score归一化方法进行数据处理，用x表示具体辅助变量的样本集合，有：

x=(x1,x2,…,xm)

(13)

式中，xi表示辅助变量的第i个样本值。

建立映射f，有：

(14)

其中，xmean为x的均值；xvar为x的方差，可分别表示为：

xmean=mean(x1,x2,…,xm)

(15)

xvar=var(x1,x2,…,xm)

(16)

根据热室圆盘锯床的工艺流程，针对切割片的磨损情况可将切削状态分为三类，分别为“正常状态”、“正磨损状态”和“负磨损状态”。在正常状态时，切割片的磨损程度较为乐观，可以依据当前切削参数继续进行切削；在正磨损状态时，切割片上面的切削粒大部分切削前角增大，可适当增加切削速度或切削深度的切削，从而提高切削效率；与正磨损状态相反，负磨损状态下切割片上的切削粒的大部分切削前角减小，此时的条件并不利于切削，因此需要相应减小切削速度。

通过上诉分析，选取切割轴转矩、切削速度、切削深度作为判断切削状态的辅助变量，首先通过伺服驱动器采集切削过程中的有效辅助变量，并根据观测到的刀具的实际磨损情况进行切削状态的分类。同时，采用Z-Score归一化方法对采集到的辅助变量进行归一化处理，得到归一化后新的辅助变量值，如表1所示。表1为切削过程中采集到的23组辅助变量样本数据，其中第1~15号样本数据作为训练数据，用以训练高斯过程分类器，第14~23号样本数据作为预测状态的验证数据，用以验证训练后高斯过程分类器的识别效果及准确率。

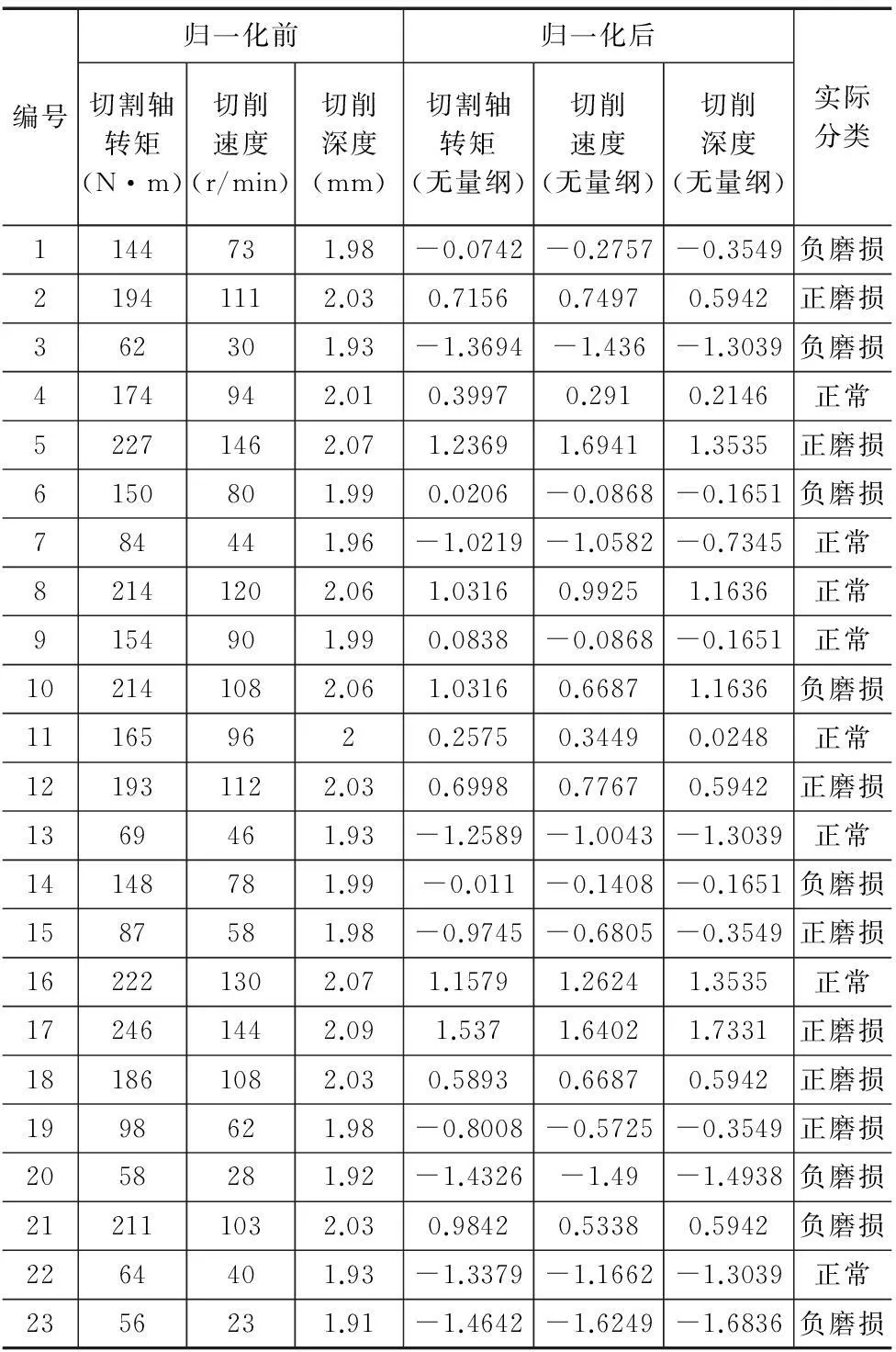
表1　切削过程实时数据样本表

2热室圆盘锯床刀具切削状态识别

根据热室圆盘锯床切削状的实际工艺和需求，在切削过程中通过切削刀具的前角大小将切削状态分为“正常状态”、“正磨损状态”和“负磨损状态”三个状态。而从分类角度来看，三状态的分类方式构成了一个三元分类问题，需要将其分解为三个二元分类问题进行解决。具体的过程如下：首先采用高斯过程二元分类方法分别预测样本数据属于正常状态、正磨损状态、负磨损状态的概率值，然后比较三个概率值，通过比较判断，属于某一状态的概率最大，就认为该样本属于这一状态。

切削状态分类GPC模型的收敛标准为：迭代步数大于等于200步或者在迭代过程中目标值的绝对差值小于1×10-6。通过辅助变量训练样本的训练，采用共轭梯度优化算法求解训练样本的似然函数的极大值，在此过程中寻优高斯过程分类模型的超参数。

按照上述规则，以GPC模型为基础，设计高斯过程分类器。结合热室圆盘锯床切削状的实际工艺和需求，以第1~15号样本数据作为训练数据用以训练高斯过程分类器，分别对辅助变量样本中第14~23号样本数据属于正磨损状态、正常状态、负磨损状态的概率进行预测，预测结果如表2所示。

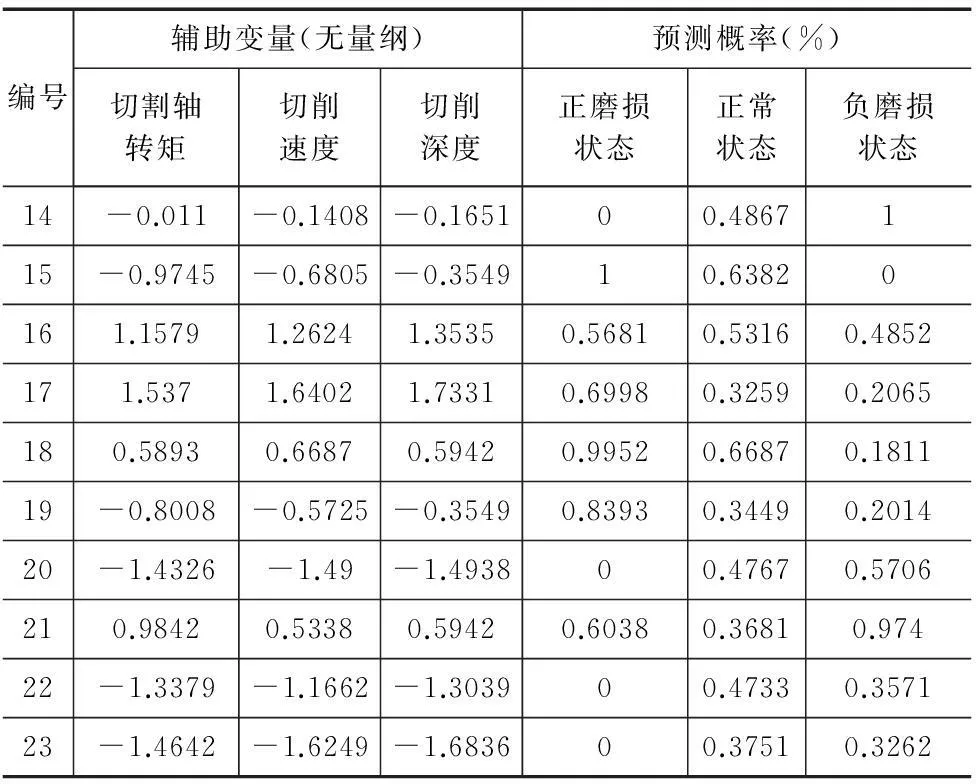
表2　三种状态下的GPC概率值

根据概率最大的原则，测试数据的分类结果如表3所示。

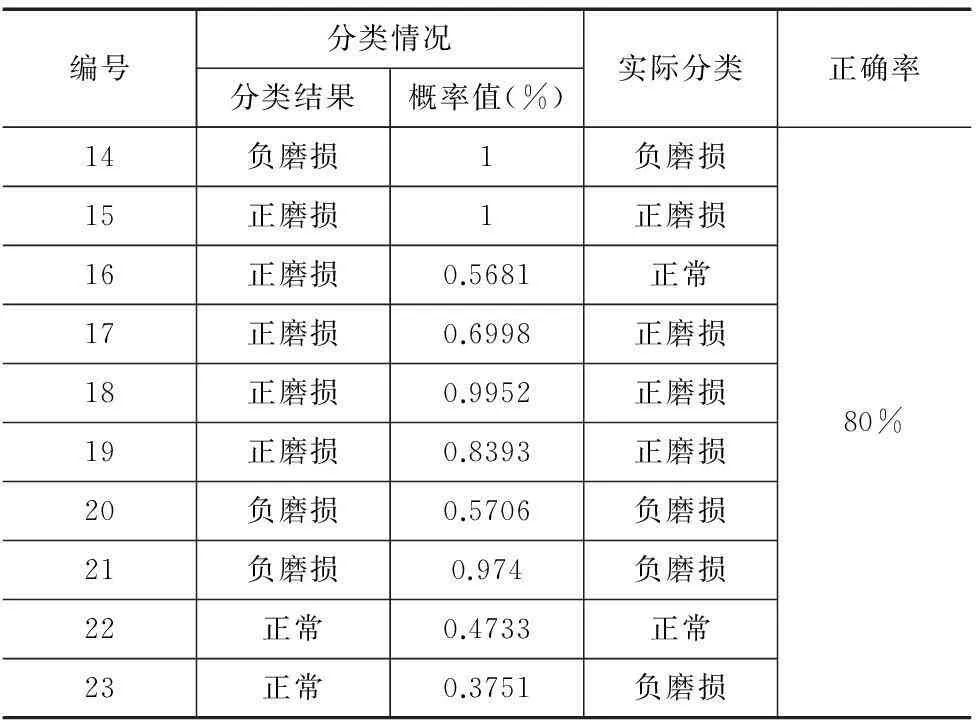
表3　切削状态分类结果表

从表3中可以看出，10组测试数据有8组分类结果与实际分类相吻合，只有第16组和第23组数据的预测切削状态与实际分类不同，正确率达到80%。

因此，针对热室圆盘锯床切削工艺选取切割轴转矩、切削速度、切削深度作为状态识别器的辅助变量，通过归一化方法进行数据处理，采用高斯过程二元分类方法对选取的辅助变量和对应的切削状态进行学习并进行状态概论的预测和识别，将预测得到的识别状态与实际状态进行对比，结果表明，利用高斯过程二元分类方法进行的热室圆盘锯床刀具切削状态的识别具有较高的识别精度和可靠性。

3结论

本文以热室圆盘锯床切削为研究背景，结合热室圆盘锯床切削的特点和工艺，选取了状态识别的辅助变量，建立了高斯过程二元分类学习和预测模型，设计了基于高斯过程二元分类的切削状态识别器，在此基础上，研究了基于高斯过程二元分类的热室圆盘锯床切削状态的识别方法。最后，通过与样本数据进行对比验证，结果表明：

(1)在热室圆盘锯床切削工艺条件下，切割轴转矩、切削速度和切削深度等状态参数可以表征切削过程中切削状态的变化的规律，可以作为判断热室圆盘锯床切削状态的辅助变量。

(2)采用高斯过程二元分类方法建立的切削状态识别器在经过样本数据的学习后，可以准确的预测识别出切削过程中刀具的切削状态。

(3)基于高斯过程二元分类的热室圆盘锯床刀具切削状态的识别方法，对于热室圆盘锯床切削的切削状态识别的正确率较高，能够很好的反应热室圆盘锯床切削过程的真实状态。

(4)本文采用的基于高斯过程二元分类的刀具切削状态预测识别方法具有通用的意义，可适用于其它切削工艺的切削状态识别问题中。

[参考文献]

[1] 孟庆鑫, 郑金兴, 张铭钧. 多传感器数据融合技术在刀具状态监测中的应用[J]. 传感器与微系统,2007，26(4)：90-93.

[2] 文西芹, 李纪明. 切削过程监测用磁弹性扭矩传感器试验研究[J]. 机床与液压,2008，36(6)：101-103.

[3] 李迎. 高速切削工艺参数优化模型研究及发展趋势[J]. 电子机械工程,2010，26(1)：1-9.

[4] 舒服华. 基于小波神经网络的刀具状态监测[J]. 组合机床与自动化加工技术,2006(1): 69-70.

[5] 冯冀宁,刘彬,刁哲军,等. 基于小波神经网络的切削刀具状态监测[J]. 中国机械工程, 2004,15(4):41-44.

[6] 徐春广,王信义,邢济收. 刀具切削状态模糊性及识别方法[J]. 北京理工大学学报,1998,18(2): 46-52.

[7] 叶洪涛,张军,杨金发,等. 航空难加工材料切削加工中的关键应用技术[J]. 航空制造技术,2012(10):44-46.

[8] 魏三喜. 基于高斯过程的多元分类方法[J]. 信息技术,2012,12(6):8-10.

[9] Bazi Y, Melgani F. Gaussian Process Approach to Remote Sensing Image Classification [J]. IEEE transactions on geoscience and remote sensing，January 2010，48(1): 186-197．

[10] Rasmussen C E, Williams C K I. Gaussian Processes for Machine Learning[M].Cambridge: The MIT press, 2006.

[11] 刘战强,吴继华,史振宇,等. 金属切削变形本构方程的研究[J]. 工具技术,2008,42(3):3-9.

[12] 陈志刚,周里群,黄霞春. 基于ANSYS的金属切削过程有限元仿真[J].凿岩机械气动工具，2007(1):46-54.

(编辑李秀敏)第

The Identification of Cutting State of Cutter Based on Gaussian Processes Binary Classification

LIN Jing-dong, YOU Jia-chuan, HUANG Li-pei, LIU Huan

(College of Automation, Chongqing University, Chongqing 400044, China)

Abstract：Based on the background of hot cell circular sawing machine cutting process, in the case of the sensor cannot be installed，this paper studied the cutting state detection and recognition problems during the cutting process. Combined with the structure characteristics of hot cell circular sawing machine, selected the servo motor torque, cutting depth and real-time cutting speed as the auxiliary variables of state recognition, based on the binary classification method of Gauss process, the cutting state recognition based on Gauss process classification is designed, after training with sample data, finally realize the classification and recognition of the cutting state of hot cell circular sawing machine. The identification results are compared with the actual cutting state, and the results show that, the method of cutting state of hot cell circular sawing machine based on Gaussian processes binary classification can effectively and accurately identify the cutting status in the working process of hot cell circular sawing machine, and can response the actual cutting state of hot cell circular sawing machine well.

Key words：gauss process; binary classification; cutting state; state recognition

中图分类号：TH166;TG506

文献标识码：A

作者简介：林景栋(1966—)， 男， 福建宁德人，重庆大学副教授，博士， 研究方向为工业自动化设计、复杂工业流程的优化控制、智能化产品设计，(E-mail)yjc_cqu@163.com。

收稿日期：2016-05-28；修回日期：2015-07-01

文章编号：1001-2265(2016)03-0104-04

DOI:10.13462/j.cnki.mmtamt.2016.03.029