基于尺度效应的超声珩磨磨削力建模及仿真

叶林征，祝锡晶，王建青，郭　策

(中北大学 山西省先进制造重点实验室，太原 030051)



基于尺度效应的超声珩磨磨削力建模及仿真

叶林征，祝锡晶，王建青，郭策

(中北大学 山西省先进制造重点实验室，太原 030051)

摘要：为从微观研究功率超声珩磨机理，考虑了材料的尺度效应，采用基于细观机制的应变梯度塑性理论(MSG)，建立了单油石磨削力模型及比磨削能模型，并对其进行了仿真分析。结果表明：考虑尺度效应时磨削力有所增大。对磨削力影响最大的参数是珩磨深度，珩磨深度低至某一阈值(约1.4μm)后，随着珩磨深度的继续减小，磨削力呈现非线性增大的趋势。当珩磨深度低于4.4μm继续降低时，比磨削能也会非线性增大。因此，材料在微尺度时变得难以切除。

关键词：超声珩磨；尺度效应；磨削力模型；比磨削能

0引言

功率超声珩磨是一种新型的精密加工方法，具有磨削力小、珩磨温度低、加工效率高等优点[1]，广泛应用于汽车和坦克缸体及缸套加工中，具有广阔的应用前景。近年来，科学家们广泛地从实验中观察到微尺度下材料表现出来的尺度效应，即加工材料的非均匀塑性变形的特征长度处于微米级时，材料的行为会显著区别于宏观尺度下的材料。1994年，Fleek等在细铜丝扭转试验中观察到，铜丝直径从170μm减小至12μm，其无量纲扭转硬化几乎增加了两倍[2]。1998年，在A.G.Evans和Stolken的超薄梁弯曲实验中观察到，随着薄梁的厚度减小，梁的弯曲强度明显增加[3]。一系列微压痕实验也表明，随着压入深度减小到微米级，实验金属的硬度有所增加[4-5]。

国内外关于磨削力模型的研究已有不少论述，但对于超声珩磨磨削力模型的介绍却并不多。李力钧将磨削力划分为切削力和摩擦力，建立了磨削力的数学模型[6]。谢桂芝[7]等研究了工程陶瓷磨削过程中发生塑性变形去除和脆性断裂去除的临界条件，分别建立了对应的磨削力模型。刘振[8]等考虑了材料的应变率，建立了超声珩磨磨削力模型。

综上所述，超声珩磨深度降低到微米级，被加工材料会不可避免地表现出尺度效应，但目前还未见其相关研究。本文基于超声珩磨加工机理，应用基于细观机制的应变梯度塑性理论(MSG理论)，考虑材料尺度效应，建立磨削力的模型，并对其进行数值仿真，分析尺度效应对磨削力及比磨削能的影响。

1超声珩磨的加工机理

珩磨中施加的超声有三种振动形式：轴向振动，径向振动，扭转振动[8]。本文选用轴向超声振动，其加工示意如图1所示。

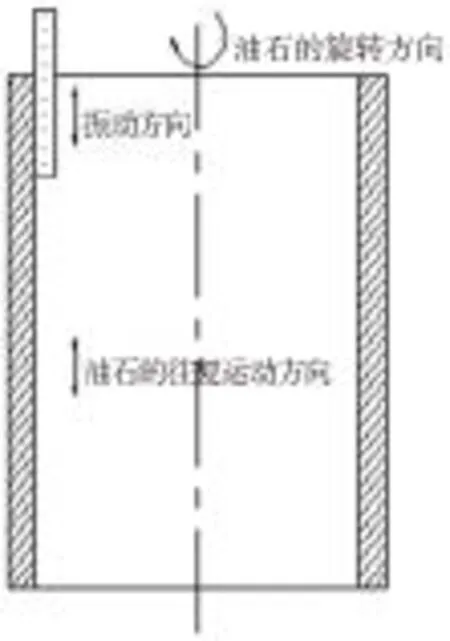
图1　轴向超声珩磨加工示意图

油石做往复及轴向旋转运动的同时，为其施加轴向超声振动，使油石的合成速度附加了正弦波的速度。假设所施加的振动形式为Asin2πft,其中A为施加的轴向振动的振幅，f为振动的频率，则油石的合成速度为：

(1)

式中，vea为油石合成速度，v为油石往复速度，va为油石旋转速度，vf为油石超声振动速度。

2功率超声珩磨尺度效应

超声珩磨的珩磨深度为几微米时，应考虑材料的尺度效应。随珩磨深度降低，被加工材料的硬度、比磨削能(或单位磨削力)出现非线性增大的现象，此即尺度效应。运用基于细观机制的应变梯度塑性理论(MSG理论)，材料的抗剪强度可由位错密度表示：

(2)

式中τ代表抗剪强度；α是一个经验常数；其值在0.2~0.5之间,这里取为0.5；μ为剪切模量；b为Burgers向量长度，对于45钢，b为0.28664nm；ρ是总位错密度；ρs为统计存储位错密度；ρG为几何必需位错密度，与微观尺度下应变梯度η的关系如式(3)所示：

(3)

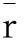
晶体中的拉伸流动应力如式(4)所示：

(4)

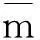
(5)

Nix和Gao发展了一种位错模型来估计圆锥形压头下面的几何必需位错密度，再结合(4)式可以得出压痕硬度和压痕深度之间的关系：

(6)

式中H0为不考虑尺度效应时的压痕硬度，对于45钢，取为1.7052；H为压痕深度为h时的硬度；h*是一个为长度量纲的参数；计算公式如式(7)所示：

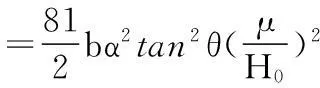
(7)

式中θ为圆锥形压头表面和被压材料表面的夹角。对于标准维氏压头，压头尖端半角为68°，所以θ=22°。

3油石磨削力模型的建立

3.1单颗磨粒磨削力模型的建立

超声珩磨中的磨削力由切削变形力和摩擦力两部分组成，对于单颗磨粒，有：

(8)

式中，g代表单颗磨粒，N代表法向力，T代表切向力，c代表切削变形力，s代表摩擦力。

将油石上的磨粒理想化为维氏压头，有如下关系：

P=ξHR2

(9)

式中，P为施加在单颗磨粒上的载荷，ξ为压头几何因子，对于维氏压头取2，H为材料的硬度，R为压痕尺寸，有R=aptanλ，ap为压入深度，λ为锥头的顶尖半角,为68°。

由于油石上的磨粒不可能与标准的维氏压头完全一样，并且在超声珩磨中存在空切削现象，磨粒不可能始终和工件接触，所以引进一个无量纲的系数η0(0<η0<1)，根据具体加工环境及实验经验，取为0.5，结合式(6)，可得法向切削变形力为：

(10)

根据单颗磨粒的受力分析以及几何条件可以得到切向切削力如式(11)所示：

(11)

对单颗磨粒，由于摩擦引起的磨削力如式(12)所示：

(12)

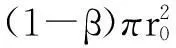
由上述可得单颗磨粒的磨削力模型如式(13)所示：

(13)

3.2单油石磨削力模型

单个油石上的有效磨粒数可估算为：

(14)

式中，b、l分别为油石的宽度和长度，dmean为磨粒的平均直径，p为油石上磨粒参与划擦和切削的百分比，有研究表明，金刚石油石表面真正参与划擦和切削的磨粒数所占的比例为3.84%和0.52%[8]。

将单颗磨粒的磨削力和油石上有效磨粒数相乘，即可得到单个油石的磨削力如式(15)所示：

(15)

3.3比磨削能计算

比磨削能是指去除单位体积材料所消耗的能量，其与切向磨削力关系密切，如式(16)所示：

(16)

Vg是单位时间内单颗磨粒去除材料的体积，由于磨粒附加了超声振动，Vg可由下式大致得到：

(17)

式中，v为未施加超声的磨粒速度，θ为磨粒顶锥半角，ap为珩磨深度，r0为磨粒平顶半径。

4磨削力模型仿真分析

为直观看出尺度效应对超声珩磨磨削力的影响，研究磨削力的变化程度及趋势，应用Matlab对上述建立的磨削力模型进行仿真分析，选用工件材料为45钢，有关油石、功率超声珩磨的仿真参数如表1所示。

表1　功率超声珩磨仿真参数

仿真结果如图2所示，磨削力的变化趋势与相关微切削分析结果趋势一致[10],结合每个图进行定量分析并给出相应的结论。

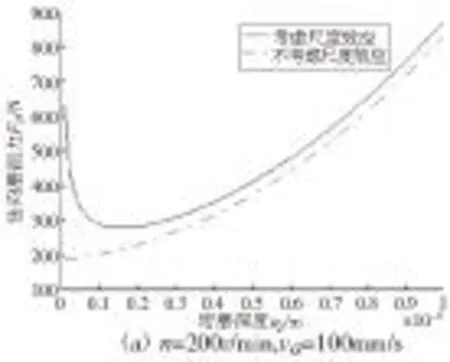
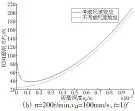
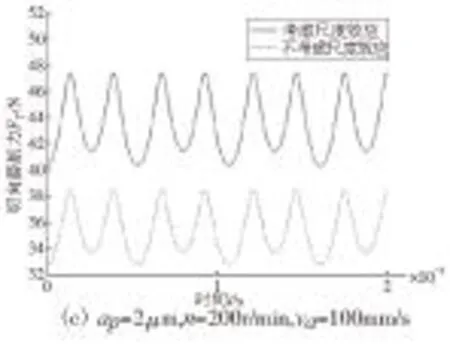
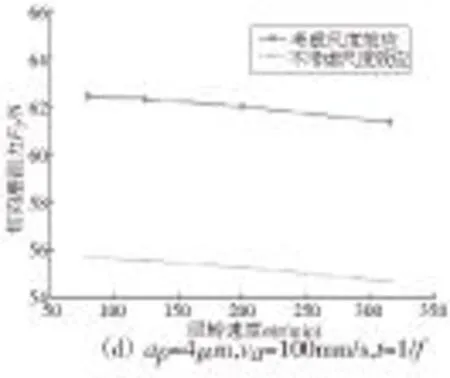
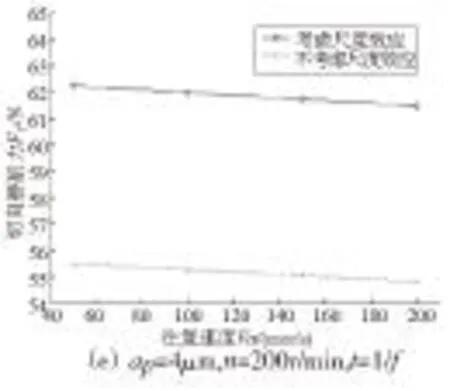
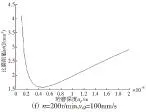
图2　磨削力、比磨削能随参数的变化曲线

附加的超声振动形式为轴向振动，对切向磨削力影响较大，而对法向磨削力影响较小，如图2c所示，切向磨削力会随时间变化而呈现周期性的振动。如图2a、2b、2d、2e所示，影响磨削力大小最主要的参数是珩磨深度，回转速度和往复速度的影响相对较小，受材料尺度效应影响，和不考虑尺度效应相比，法向磨削力和切向磨削力均有所增大。从图2a、2b可以看出，随珩磨深度减小，法向磨削力和切向磨削力呈非线性变化趋势，其规律为先随珩磨深度的减小而减小，当珩磨深度达到某一特定值(约1.4μm)时，磨削力达到最小，若珩磨深度继续减小，磨削力则呈现急剧增大的现象，使材料难以去除。这是由于在微尺度下材料的一些特性发生变化，要全面考虑材料的晶格位错，材料硬度增加，抗剪强度以及拉伸流动应力也有所增大，磨削力增大；当大于这一特定值时，逐步趋向于宏观切削，磨削力随珩磨深度的增加而增大,这也解释了珩磨实验中珩磨深度为1μm时材料无法有效去除[11]的原因。当珩磨深度低至某一值(约4.4μm)继续减小时，比磨削能也出现非线性增大的现象，表现出越小越难切的现象。随着回转速度或往复速度的增加，磨削力有微量的降低，这是由于油石速度的增加会降低动摩擦系数从而降低磨削力。

5结论

(1)当功率超声珩磨的珩磨深度为几微米时，应当考虑材料的尺度效应，这对研究超声珩磨的微观机理是很必要的。

(2)建立的磨削力模型与被加工材料的微观参数有关，如材料Burgers向量长度。

(3)考虑尺度效应时的磨削力明显大于不考虑尺度效应的情况，且珩磨深度低于1.4μm时，随珩磨深度降低，法向磨削力以及切向磨削力均出现非线性的增大，解释了珩磨深度太低时材料无法有效去除的原因。随油石相对速度的增加，磨削力有微量的降低。

(4)当珩磨深度低于4.4μm时，随珩磨深度的降低，比磨削能出现非线性增大，使材料在微尺度时变得难以切除。

[参考文献]

[1] Zhu X J, Wang J Q, Cheng Q, et al. Radial power ultrasonic vibration honing friction analysis[J]. Solid State Phenomena, 2011, 175: 183-186.

[2] 张涛, 刘战强, 许崇海. 基于有限元法的微径铣刀变形分析[J]. 组合机床与自动化加工技术, 2012 (5): 1-5.

[3] 庄茁, 崔一南, 高原, 等. 亚微米尺度晶体反常规塑性行为的离散位错研究进展[J]. 力学进展, 2012, 41(6): 647-667.

[4] Fuguo L, Jinghui L, Bo C, et al. Size Effects at Dwell Stage of Micro-Indentation for Pure Aluminum[J]. Rare Metal Materials and Engineering, 2014, 43(12): 2931-2936.

[5] 魏悦广, 王学峥, 武晓雷, 等. 微压痕尺度效应的理论和实验[J].中国科学(A辑), 2000,30(11):1025-1032.

[6] 江卓达, 何永义. 磨削颤振特性研究进展[J]. 制造技术与机床, 2012 (9):35-42.

[7] 谢桂芝,尚振涛,盛晓敏,等.工程陶瓷高速深磨磨削力模型的研究[J]. 机械工程学报,2011, 47(11): 169-176.

[8] 刘振,祝锡晶,王建青,等.轴向功率超声珩磨力学模型的建立及仿真[J].机械科学与技术, 2014, 33(6)；858-863.

[9] 郭建英.基于不同刀-屑摩擦模型的金属切削过程动力学研究[D]. 太原: 太原理工大学, 2010.

[10] 张涛.微切削加工单位切削力及表面加工质量的尺寸效应研究[D].济南:山东大学,2013.

[11] 祝锡晶.功率超声振动珩磨技术的基础与应用研究[D].南京:南京航空航天大学, 2007.

(编辑李秀敏)

Modeling and Simulation of Grinding Force on Ultrasonic Honing Based on the Scale Effect

YE Lin-zheng, ZHU Xi-jing, WANG Jian-qing, GUO Ce

(Key Laboratory for AMT of Shanxi，North University of China，Taiyuan 030051，China)

Abstract：In order to research the mechanism of power ultrasonic honing from the microcosmic, considering the scale effect of the material, using the strain gradient plasticity theory based on the dislocation mechanism (MSG), establishing a single whetstone grinding force model, the specific grinding energy model, then simulating and analyzing them, simulation results show: the same trend with a series of other micro-cutting researches. The most influential parameter on the grinding force model is honing-depth, when honing-depth reduces to a certain threshold (about 1.4μm), with the honing-depth continuing to decrease, grinding force shows the trend of nonlinear increase. When the honing-depth is less than 4.4μm then decreases, the specific grinding energy also increases nonlinearly. Therefore, the material becomes difficult to removal under the microscale.

Key words：ultrasonic honing; scale effect; grinding force model; specific grinding energy

中图分类号：TH162;TG580.67

文献标识码：A

作者简介：叶林征(1990—)，男，河北廊坊人，中北大学博士研究生，研究方向为功率超声珩磨，(E-mail)lz09020141@163.com；祝锡晶(1969—)，男，山西太原人，中北大学教授，博导，博士，研究领域为精密与特种加工，(E-mail)zxj161501@nuc.edu.cn。

*基金项目：国家自然科学基金资助项目(51275490,50975265)；山西省自然科学基金(2013011024-5)

收稿日期：2015-04-15；修回日期：2015-05-09

文章编号：1001-2265(2016)03-0064-03

DOI:10.13462/j.cnki.mmtamt.2016.03.018