ZC1圆弧圆柱蜗杆传动强度分析*

靳小马,吉卫喜,2

(1.江南大学 机械工程学院，江苏 无锡　214122；2.江苏省食品先进制造装备技术重点实验室, 江苏 无锡　214122)



ZC1圆弧圆柱蜗杆传动强度分析*

靳小马1,吉卫喜1,2

(1.江南大学 机械工程学院，江苏 无锡214122；2.江苏省食品先进制造装备技术重点实验室, 江苏 无锡214122)

摘要：对ZC1蜗杆传动强度进行了研究，基于啮合理论、赫兹理论和ZC1圆弧圆柱蜗杆的强度解析式，并结合有限元建立了蜗杆副的接触模型，将计算得到的应力结果与解析式计算的应力进行对比。解析式算法结果略大于有限元法结果的11.5%~15.5%，验证了有限元法的正确性，可以作为ZC1蜗杆副啮合的强度计算依据。并且研究了蜗杆啮合过程中的齿间载荷分配情况，得出第一对啮合齿的承受主要的扭矩，约占总负荷的60%~72.3%。接触应力沿蜗轮齿长方向的分布形状为U形。

关键词：蜗杆传动；有限元法；强度分析；解析法

0引言

ZC1圆弧圆柱蜗杆具有轮齿弯曲强度高、承受冲击载荷高、诱导法曲率半径较小、齿面接触应力较小、传动效率高的优点[1]。目前，研究ZC1蜗杆传动强度的文献比较少，其承载能力校核主要参考王树人教授编著的《圆弧圆柱蜗杆传动》，但是介绍传动强度的篇幅小，难以满足强度设计所需的参数选择。李秀珍[2]将有限元法与埋丝法测试实验结合起来并得到了令人满意的结果，有一定的借鉴意义。马东[3]基于齿轮空间啮合原理，通过Matlab建立ZN蜗杆的齿面数学模型，并分析了接触线形状的影响因素，为双导程ZN蜗杆的强度、承载能力的计算奠定了基础，但研究对象不是ZC1蜗杆。李宁[4]结合啮合原理、赫兹弹性接触理论，用解析法详细计算一个啮合周期的齿面接触强度，并用有限元法进行验证。Daizhong S[5]和Simon V[6]以计算机为辅助利用数值计算法对三维应力分布进行了研究。张驰[7]应用有限元方法对柔性齿轮进行模态分析,利用Pro/E建立柔轮几何模型，导入ANSYS中定义不同的材料属性研究其振动特性。张振军[8]和张彦钦[9]基于有限元法对轮齿的强度计算进行解析法与数值法结果的对比。张学刚[10]基于渐开线齿轮的成形原理和啮合原理，结合Matlab和Pro/E完成了渐开线圆柱齿轮的精确三维模型，为后续的齿轮强度分析奠定基础。

蜗杆副在啮合的过程中最常见的失效形式以齿面点蚀和齿根磨损最为常见。为保证蜗杆副能够在使用寿命内正常平稳的工作，蜗杆尤其是蜗轮齿面应有一定的接触疲劳强度来抵抗点蚀，同时也应具有一定的齿根弯曲强度来抵抗磨损的破坏。因此，本文对ZC1圆弧圆柱蜗杆进行齿面接触应力与齿根弯曲应力的分析是很有必要的。

本文根据啮合原理、赫兹理论，和适合工程应用的强度计算公式计算得到应力的解析式计算结果。基于非线性接触理论和有限元法，建立了ZC1圆弧圆柱蜗杆传动副的有限元接触模型，将有限元计算结果与解析法进行比较。并且分析了蜗杆传动过程中的齿间载荷分配和应力沿蜗轮齿长方向的分布形状。

1ZC1蜗杆副强度解析法

1.1齿面疲劳点蚀计算

青铜制的蜗轮的强度相对于钢制的蜗杆较低，所以蜗轮是强度计算的主要对象。齿面接触应力的大小，不仅是齿面疲劳点蚀的诱因，也会导致齿面磨损和胶合现象的出现。所以齿面接触应力是蜗杆传动承载能力强弱的主要依据之一。蜗轮的接触应力可用赫兹应力表达，即：

(1)

可将材料弹性系数简化为：

(2)

于是式(1)可简化为：

(3)

式中：μ1,μ2—材料的泊松比；

σH—齿面接触应力；

l—蜗轮齿面的接触线总长；

Fn—作用在蜗轮齿面的法向力；

E1，E2—蜗杆与蜗轮材料的弹性模量；

ρn—垂直于蜗轮齿面的接触线的法面当量曲率半径。

由于在啮合过程中接触线总长l与法面当量曲率半径ρn不断变化，求解困难，在假设赫兹应力沿各条接触线能达到均匀分布的前提下，应用微元法推导计算蜗轮齿面接触应力的计算公式[11]：

求解单位载荷：

(4)

将上式两边对接触线l微元化处理：

(5)

如图1所示。

图1　齿面接触点处的夹角λ

接触线微元dl上的法向力dFn可分解为沿蜗杆轴线方向的切向力dFn1=dFncosλ,λ为作用于接触线微元dl的法向力Fn与蜗杆轴向方向的夹角。

将Fn1转化为蜗轮转矩T2的关系，即：

dT2=dFn1dm2/2=dFncosλdm2/2

(6)

代入式(5)，得：

(7)

将(7)式积分，得：

设x=1~n为一个蜗杆齿距内同时啮合的瞬时接触线的数目，则：

最后通过计算机计算，并进行相应的简化得到的蜗轮齿面接触强度公式为：

(8)

式中：

Zρ—接触系数；Zρ=2.05(dm1/a)-0.34，可查图2得；

a—中心距，mm；

T2—输出转矩，N·m。

图2　圆柱蜗杆传动的接触系数Zρ

1.2抗磨损承载能力计算

蜗轮的轮齿是一种倾斜的弧状曲梁形状，由于轮齿截面形状太过复杂，各个截面上的齿形沿着齿宽的方向是不一样的，但根据工程实际，可知齿根弯曲强度主要和模数m以及齿宽b2这两个主要的参数有关。一般参照普通圆柱蜗轮齿轮作近似计算，验算公式为：

σF=Ft2KA/mb2

(9)

Ft2=2000T2/dm2

(10)

dm2=2a′-d1

(11)

根据式(10)和(11)中的Ft2和a′、d的关系，联立式(9)、(10)、(11)得到更方便计算的弯曲应力解析式：

(12)

式中：σF—齿根弯曲应力；

T2—蜗轮扭矩；

KA—使用系数；

m—蜗杆轴向模数；

b2—蜗轮齿宽；

a′—啮合中心距，约等于中心距a；

d1—蜗杆分度圆直径。

2蜗杆副有限元接触强度计算分析

根据圆弧圆柱蜗杆ZC1的啮合理论，编程计算蜗杆端面齿廓坐标点，利用B样条曲线生成端面齿廓，再利用ANSYS中的apdl语言参数化编程，最后生成蜗杆的三维造型，用相似方法亦可得到与之匹配的蜗轮三维造型。利用ANSYS生成有限元接触模型，体单元为Solid64,使用Targel170和Contal174来定义接触对，蜗杆模型划分成42134个节点和61214个体单元。蜗轮模型划分成32358个节点和53520个体单元，有限元模型的网格划分如图3所示。

图3　有限元模型网格划分

定义载荷与约束：约束蜗轮的内圈的全部自由度，约束蜗杆除绕自身轴线的转动自由度以外的X,Y,Z方向上的移动自由度，在蜗杆两轴端施加均匀切向载荷，形成扭转载荷，总的载荷即为转动载荷T1。

蜗杆副的材料：蜗杆材料为20CrMnTi，弹性模量E1=199GPa，泊松比μ1=0.27，密度为7827Kg/mm3；蜗轮材料为QSn6.5-0.1，弹性模量E2=103GPa,泊松比μ2=0.3，密度为8850kg/mm3。

蜗杆副参数为齿数Z1=6,Z2=41,模数m=20mm，蜗轮变位系数x2=0.375，蜗轮中圆直径dm2=835mm，啮合中心距a′=500mm，蜗杆节圆直径d1=165mm，蜗轮节圆直径d2=820mm，蜗轮齿宽b2=115mm，额定转矩T2=15500N·m。

对蜗杆施加扭矩1500N·m，受载荷最大的1号齿上的接触应力沿接触线呈U分布。将计算的数据通过B样条曲线拟合处理为曲线，如图4所示。

图4　第1号齿上接触应力分布

表1为输入不同扭矩(N·m)分别为200、1000、1500、2240时，各个参与啮合传动的齿所受齿间载荷分配。由表1可以看出，啮入齿即1号齿承受载荷最大；随着载荷不断增大，1号齿承受载荷分配比不断减少，但仍然占了很大的比例，最大齿间载荷分配从72.3%下降到60.2%。

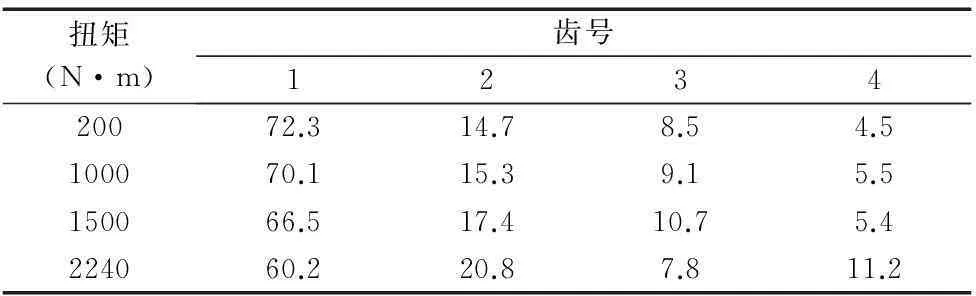
表1　齿间载荷分配表(%)

3有限元法与解析法结果对比

如表2所示，解析式算得的齿面接触应力结果均大于有限元法得到的数值，大约高了11.5%~13.6%。

如表3所示，解析式算得的齿根弯曲应力结果均大于有限元计算的结果约13.8%~15.5%。

由此可见有限元法比解析法略精确，解析法略保守，并不能精确计算ZC1蜗杆副的承载能力，但也有较好的计算精度。

表2　齿面接触应力对比(MPa)

表3　齿根弯曲应力对比(MPa)

4结论

(1)基于赫兹理论，对ZC1蜗轮的齿面接触应力解析式和齿根弯曲应力的公式进行了研究和阐述。

(2)基于有限元法，对ZC1蜗杆副传动的接触应力进行分析，得出第一对啮合齿的承受主要的扭矩，约占总负荷的60%~72.3%，应力大小沿蜗轮齿长方向呈U形分布。这正好与点蚀较易发生在节线靠近齿根的部分，且蜗轮齿面两端较易产生疲劳点蚀的工程实际相符合。

(3)通过有限元法和解析式法的对比，解析式算法结果略大于有限元法结果的11.5%~15.5%，这是因为解析式法只计算节点处的应力大小。这说明：解析式应力计算方法偏于保守，基于有限元法的ZC1蜗杆传动的强度分析是切实可行的，能够为蜗轮蜗杆的承载能力计算和设计制造提供理论依据。

[参考文献]

[1] 王树人.圆弧圆柱蜗杆传动[M].天津:天津大学，1991.

[2] 李秀珍, 鲁宝香. ZC1 蜗杆传动变形的有限元分析[J]. 机械设计与研究, 1999 (2): 52-53.

[3] 马东, 黄筱调, 于春建. 基于 Matlab 的双导程 ZN 蜗杆建模及其接触线特性分析[J]. 组合机床与自动化加工技术, 2014 (2): 57-59.

[4] 李宁, 李威. 渐开线斜齿圆柱齿轮齿面接触强度分析[J]. 机械传动, 2014，38(3): 151-153.

[5] Daizhong S, Datong Q, Zeliang P. Computer-aided design and analysis and experimental investigation of cylindrical involute worm gear drives[C]//Proceeding of the 2004 the Eleventh World Congress in Mechanism and Machine Science. Beijing: China Machine Press. 2004: 732-738.

[6] Simon V. Stress analysis in double enveloping worm gears by finite element method[J]. Journal of Mechanical Design, 1993, 115(1): 179-185.

[7] 张驰, 张琳. 谐波传动中不同材料柔性齿轮的有限元分析[J]. 组合机床与自动化加工技术, 2014(3): 137-139.

[8] 张振军,郑昆,王征,等.基于Pro/e 的齿轮传动疲劳强度有限元分析[J]. 精密制造与自动化, 2014 (1): 14-16.

[9] 张彦钦, 张光辉. 平面二次包络环面蜗杆传动强度计算[J]. 西南交通大学学报, 2011, 46(1): 138-142.

[10] 张学刚, 谢永春. 渐开线圆柱齿轮全参数化精确建模研究[J]. 组合机床与自动化加工技术, 2013 (7): 46-48.

[11] 叶克明, 石风山, 丁淳. 齿轮手册[M]. 北京: 机械工业出版社, 1990.

(编辑李秀敏)

Drive Strength Analysis of ZC1 Circular Cylindrical Worm

JIN Xiao-ma1,JI Wei-xi1,2

(1.School of Mechanical Engineering, Jiangnan University, Wuxi Jiangsu 214122, China;2. Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment and Technology, Wuxi Jiangsu 214122, China)

Abstract：Strength of ZC1 worm drive is studied.Based on meshing theory, hz theory and the intensity of ZC1 circular cylindrical worm, the contact model of worm pair is established combining with the finite element.The calculated stress results compare with analytical calculation of stress.Analytical algorithm results slightly bigger than the finite element method of 11.5%~15.5%.The finite element method is validated the correctness and can be used as the strength calculation basis of ZC1 worm pair meshing.Load distribution among gear teeth has been studied in the process of worm gearing, it is concluded that the first pair of meshing teeth under the main torque, accounts for about 60%~72.3% of total load .The distribution of contact stress along the direction of worm gear teeth shapes for U.

Key words：worm drive;the finite element method;strength analysis;analytical method

中图分类号：TH166;TP132.4

文献标识码：A

作者简介：靳小马(1991—)，男，江苏徐州人，江南大学硕士研究生，研究方向是机械制造及其自动化，(E-mail)jxm2018@126.com；通讯作者：吉卫喜(1961—)，男，江苏姜堰人，江南大学教授，博士，研究方向为先进制造技术、产品数字化设计及制造。

*基金项目：江苏省产学研联合创新资金(BY2014023-30)

收稿日期：2015-05-28；修回日期：2015-07-01

文章编号：1001-2265(2016)03-0055-03

DOI:10.13462/j.cnki.mmtamt.2016.03.015