RV减速器中摆线轮齿形优化修形与参数化设计*

张跃明，耿纪玲，纪姝婷，朱国杨

(北京工业大学 机械工程与应用电子技术学院，北京　100124)



RV减速器中摆线轮齿形优化修形与参数化设计*

张跃明，耿纪玲，纪姝婷，朱国杨

(北京工业大学 机械工程与应用电子技术学院，北京100124)

摘要：为了得到符合实际工作要求的摆线轮齿形，对摆线轮齿形的几种修形方式进行了研究，确定了最佳修形方式为负移距与正等距相组合的修形方式。对多种优化方法进行了分析，选取了两点外插的混合罚函数法来求解，并借助VC++6.0编写绘图程序验证了此种修形方式的合理性。同时利用Pro/E 4.0对摆线轮进行了参数化设计，推导出摆线轮齿廓曲线上的坐标点按齿廓曲线曲率不同分布疏密程度不同的公式，同时借助VC++6.0编制程序计算出摆线轮齿廓曲线上分布的各点的坐标值，为使用数控机床加工摆线轮提供了便利。

关键词：摆线轮 ；优化修形；绘图程序验证；参数化设计

0引言

RV减速器主要由行星架、中心轮、摆线轮等构件组成，它具有很高的的疲劳强度、刚度和寿命，而且回差精度稳定。因此世界上许多国家高精度机器人传动常采用RV减速器。同时由于RV减速器中应用的摆线针轮传动具有体积小、传动比范围大、效率高、工作可靠、噪声低等优点，这种传动方式在很多行业中也得到广泛的应用。

由于实际应用RV减速器时，都必须要对其中的摆线轮的标准齿形进行修形，确定正确可行的修形方式是很重要的一部分。文献[1-2]提出了一种符合共轭条件的修形方式，优化了摆线轮的齿形。课题所确定的摆线轮齿廓优化修形方法是综合考虑多方面的因素之后所得的结果，弥补了以前所用修形方法的不足，同时在优化目标函数求解最佳修形量也采用了一种新的优化方法，求出的修行量更加可靠，再结合VC++6.0工具绘图来验证修形方式的合理性，这种验证手段能够更为客观地检验所用的修形方式是否能够满足RV减速器多方面的要求。此外，本课题充分考虑了摆线轮齿廓曲线在用数控机床对其进行加工过程中由于刀具进给的步长因素产生的误差，由于摆线轮齿廓曲线的曲率是变化的，根据曲率的变化来推导摆线轮齿廓曲线上点的分布规律，并借助VC++6.0编制程序计算摆线轮齿廓曲线上点坐标，这与平均分布点坐标的方法相比，加工精度在理论上提高了许多。

1摆线轮齿形的修形方法的确定

为补偿制造时的尺寸链误差，便于装拆，保证润滑，摆线轮齿和针轮齿之间必须有合理的齿侧间隙Δc和径向间隙Δj，因此实际应用RV减速器时都要对摆线轮的标准齿形进行修形。常见有以下三种修形方式[3]：

(1)移距修形法；

(2)等距修形法；

(3)转角修形法。转角修形磨出的摆线轮与标准针轮的齿根和齿顶部分将存在无间隙接触，故不能单独使用。

合理的摆线轮齿形需满足以下要求[4]:

(1)摆线轮工作部分的齿形与针齿应尽可能地互为共轭齿形，从而使传动比恒定，运动精度高，传动平稳，达到多齿同时啮合的良好状态，增大啮合刚度来减少轮齿因弹性变形引起的回差。

(2)在摆线轮齿根与齿顶附近必须要产生合理的径向间隙，并在齿侧产生合理的齿侧间隙，用来补偿制造误差，保证良好的润滑状态。

(3)磨削工艺应简单，尽可能地减小综合回差，使初始间隙达到最小。

单独采用移距或等距修形不能形成接近共轭齿廓的齿形，转角修形虽然可以形成共轭齿廓，但是由于此方法调整繁琐，磨削效率成倍降低，一般在实际生产中不被采用，因此采用移距与等距组合的修形方法。

正移距与正等距组合修形虽可得接近共轭齿廓的齿形，但是难以满足间隙回差小的要求，此方法若保证了径向间隙，便会增加新的侧隙[5]。在单独采用等距或移距修形时，由于移距修形产生的初始间隙大于等距修形产生的初始间隙，故等距修形的效果要优于移距修形。同时在要求相同的径隙条件下，为保证获得最小的初始间隙，需采用负移距与正等距相组合的修形方法[6]。此方法不仅使摆线轮工作部分的齿形与针轮应最大限度地互为共轭齿形，形成合理的径向间隙和齿侧间隙，且能满足综合回差小的要求。

2摆线轮齿形修形的优化求解

2.1摆线轮齿形优化修形的数学模型

在根据已知的主要参数rp、zp、zc优化确定了针轮中心圆半径rrp和摆线针轮传动的偏心距a后,得出了为补偿制造误差与保证润滑条件所需要的合理的齿侧间隙Δc和径向间隙Δj，用Δc确定与摆线轮工作齿形部分所需的相吻合的转角修形齿形的转角修形量δc。

转角修形摆线轮齿形坐标公式[3]为：

(1)

移距修形与等距修形组合的摆线轮齿形坐标公式[3]为：

(2)

参考确定摆线轮啮合齿形工作范围的方法[7]，初步确定与δ=δc的转角修形齿形相吻合的摆线轮齿形工作部分应在25°~100°之间，并在此区域将φ值等分为m-1等份，建立的目标函数为：

其约束条件为：Δrrp>0，Δrp<0，Δrp+Δrrp=Δj>0。

2.2Matlab优化求解方法

Matlab优化工具箱[8]对初值依赖敏感，常采用fmincon函数优化得到的效果并不佳，如何求解出上述数学模型的最优解是非常关键的一部分，文献对多种优化方法进行了研究，确定了一种更好的求解方法为两点外插的混合罚函数法。混合函数法是通过一系列的罚因子{ci}，求罚函数的极小点来逼近原约束问题的最优点。外点罚函数法是从可行域外部向约束边界逐步靠拢的，内点罚函数法是用可行域内部的点列来逼近最优解。两点外插的混合罚函数法综合了外点罚函数的优点和内罚点函数的优点，初始点可以任意取，可以求出近似最优点，而且比混合罚函数法的求解速度快。

2.3Visual C ++6.0绘图验证

Visual C++6.0由Microsoft开发，是一个基于Windows操作系统的可视化集成开发环。运用Visual C++6.0编写绘出摆线轮齿形程序，并编写摆线轮参数输入初始界面如图1，在设计的人机交互界面[9]灵活地更改摆线轮的参数值，得到不同摆线轮的图形，同时可以输入摆线轮的修形量来绘出修形后的摆线轮齿形，可以在同一个窗口中输出摆线轮未经修形的齿形和摆线轮经过修形之后的齿形，方便比较摆线轮修形前后的变化，容易验证修形后的摆线轮齿形是否合理。

图1　摆线轮参数输入初始界面

3修形实例

一台一齿差RV减速器，针齿中心圆半径r=52.5mm,针齿半径rrp=2.25mm,针轮齿数zp=40，摆线轮齿数zc=39，偏心距a=1mm为算例。

运用上述数学模型和优化求解方法，编写Matlab程序。首先要编写出简化目标函数的程序文件，然后编写优化程序文件，取初始点x0=[-0.1 0.1]，罚因子r0=2，缩小系数c=0.5，自变量向量var=[drp drrp]。经过计算机运算，得出移距修形量为Δrp=-0.368mm，等距修形量为Δrrp=0.569mm。

在Visual C ++6.0中编出摆线轮绘图程序画出摆线轮图形来表明修形的合理性。编出输入上述实例参数后的程序界面如图2所示。在这个程序界面中，还可以输入其它型号的RV减速器的摆线轮参数，这样大大简化了摆线轮的绘图过程。

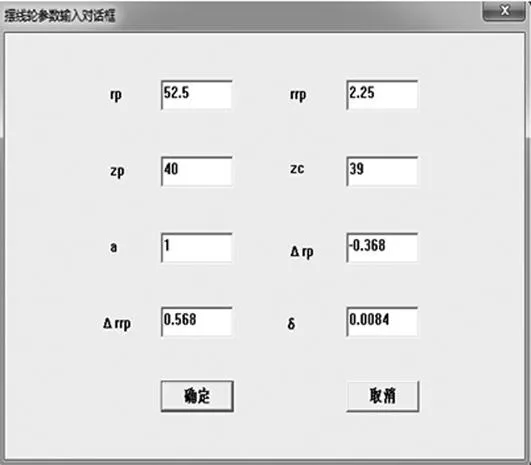
图2　摆线轮参数输入后的程序界面

在摆线轮相关参数全部输入上述程序界面之后，计算机就会在程序窗口中绘出摆线轮未经修形的齿形，摆线轮经过正等距和负移距组合修形之后的齿形以及摆线轮经过转角修行后的齿形如图3。将图3中齿形分为3段，AB为摆线轮轮齿根段，BC为摆线轮轮齿工作段，经过正等距与负移距组合修形后的摆线轮齿形与经过转角修形之后的摆线轮齿形在轮齿工作区BC段基本吻合，形成了合理的侧隙，摆线轮轮齿与针轮轮齿在工作段逼近共轭齿廓，同时在摆线轮齿根与齿顶出产生了合理的径向间隙。本例摆线轮经过修形之后得到了合理的摆线轮齿形。

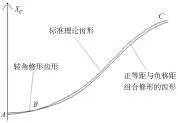
图3　修形所得的摆线轮新齿形

4摆线轮参数化设计

4.1Pro/E 4.0参数化设计的基本原理

由于已经知道摆线轮的等距与移距组合修形后的齿形方程式，便可以方便地利用Pro/E 4.0对摆线轮进行参数化设计。Pro/E 4.0操作简单方便，能快速地根据所给的参数及齿形方程绘出需要的图形，并转化为三维实体模型[10]。

4.2摆线轮参数化设计的主要步骤

(1)设置摆线轮参数。进入Pro/E 4.0零件建模界面后，执行“工具/参数”命令，输入摆线轮的设计参数：针齿中心圆半径rp、针齿半径rrp、偏心距a、针轮齿数zp、摆线轮齿数zc、等距修形量Δrrp、移距修形量Δrp。

(2)创建摆线轮齿形基准曲线。执行“插入/基准曲线”命令，选择“从方程”方式创建基准曲线，接着选取默认的坐标系和笛卡尔坐标系，然后在“方程编辑器”记事本中输入一些参数之间的约束关系式和摆线轮齿形方程在Pro/E 4.0中相应的表达式，如图4所示。最后保存并退出记事本，便可完成摆线轮单齿的齿形曲线的绘制。

图4　摆线轮修形后齿形方程式

图5　摆线轮实体模型

(3)创建摆线轮单个齿。执行“拉伸”命令，选择通过边创建图元，然后从曲线的两端到圆心连成封闭图形，点击确定后即可绘图单个齿的实体模型。

(4)创建完整的摆线轮模型。执行“阵列”命令，绘出摆线轮的所有齿的实体模型，然后执行“去除材料的拉伸”命令绘制出摆线轮上的孔。绘制好的摆线轮模型如图5所示。

4.3摆线轮齿廓曲线上坐标点分布计算

由于摆线轮的齿廓曲线的曲率是变化的，若使用数控机床对其进行加工，数控机床的刀具行程会因步长的限制无法按照实际给定的坐标位置行走，造成加工精度下降甚至无法满足我们高精度的要求，为了弥补这种不足，在考虑曲率的情况下，推导出摆线轮齿廓曲线上坐标点的分布规律与曲率的关系式如下：

(3)

式中：n—摆线轮某段齿廓曲线上分布的坐标点数；φ—转臂相对于某一针齿中心矢径的转角(°)；

摆线轮齿廓曲线的曲率：

摆线轮齿廓曲线的曲率与其上点分布疏密程度关系系数：

(4)

式中：N—摆线轮单个齿齿廓曲线上总点数；

并借助VC++6.0编制了程序方便地计算出齿廓曲线上分布的各点坐标值便于数控系统加工摆线轮，同时绘制了上述实例4中的摆线轮单个齿齿廓曲线图及其上的坐标点分布情况如下图6所示。

利用此程序可以很方便地计算摆线轮齿廓曲线上分布点的坐标并可以清楚地观察出点的分布情况，这为数控机床加工摆线轮提供了理论依据。

图6　摆线轮单齿齿廓曲线

5结论

(1)在多种修形方式中优选了负移距与正等距组合的修形方式，并用VC++6.0编程验证了这种修形方式可以获得合理的摆线轮齿形，提高了绘制各种型号的摆线轮齿形的效率。

(2)分析了优化摆线轮齿形的数学模型，选用了一种更好的新的求解方法：两点外插的混合罚函数法，能够更快速更高效地求解出理想的修形值。

(3)运用Pro/E 4.0对摆线轮进行参数化设计，与传统建模方法相比，提高了建模效率，大大地缩短了设计周期，提高了精度，同时也为对其进行仿真和有限元分析提供了模型基础，推导出摆线轮齿廓曲线上点坐标分布与曲率的关系公式，并编写了计算坐标点的程序，既提高了数控机床加工摆线轮的精度，同时简化了计算坐标的过程。

[参考文献]

[1] 肖君君．RV减速器的动态特性理论分析[D]. 大连：大连交通大学，2008．

[2] 于成国．环板式针摆行星传动非线性动力学研究[D].大连：大连交通大学，2009．

[3] 程乃士.减速器和变速器设计选用手册[M].北京：机械工业出版社，2007.

[4] 李力行．摆线针轮行星传动的齿形修正及受力分析[J]. 大连铁道学院学报，1984(4)：29-39．

[5] 姜涛，孙利民,刘凯.摆线轮齿形的组合修形方式及其优化设计[J].郑州工业大学学报，1999 ，20(3):54-56.

[6] 张世安.摆线针轮行星传动中摆线轮最佳修形量的分析与计算[J].机械科学与技术，2002，21(6):906-908.

[7] 李力行．机器人用高精度RV减速器传动的研究[J].大连铁道学院学报，1999，20(2)：1-10．

[8] 龚纯，王正林.精通MATLAB最优化计算[M].北京：电子工业出版社，2011.

[9] 雷蕾，关天民，施晓春，等. 摆线轮检测的参数化设计及绘图系统研究[J].机械设计与制造，2006(12):81-83.

[10] 曾祥亮，张屹.基于Pro/E的摆线轮参数化设计[J].装备制造技术，2009(8): 58-59.

(编辑李秀敏)

申请优先审稿须知

为振兴我国机械装备制造业，弘扬民族科学文化精神，提升期刊质量，本刊从即日起，凡是符合本刊报道范围且同时受到“国家863计划资助项目”、“国家自然科学基金资助项目”、“国家重点科技攻关资助项目”等国家级基金资助项目的原创论文，可申请优先审稿，一经录用，优先发表，欢迎业内人事、专家、学者踊跃投稿(来稿注明：“优先审稿”字样)。

注：本刊正常审稿时间一般为一个月，优先审稿时间为15-20天。

Modification and Optimization of Parameter Design of Cycloidal Gear of RV Gear

ZHANG Yue-ming，GENG Ji-ling，JI Shu-ting，ZHU Guo-yang

(College of Mechanical Engineering and Applied Electronics Technology,Beijing University of Technology,Beijing 100124,China)

Abstract：In order to meet the requirements of the tooth profile of cycloidal gear, several modificate methods were analyzed, and the selection is equidistant from the combination of a negative shift of the modificae methods of cycloidal gear.A variety of optimizate methods are studied, the method of mixed penalty function points extrapolation. To solve, and using the VC++6.0 to write a drawing program to verify the rationality of the modificae methods. At the same time, using the Pro/E 4 pairs of cycloid gear parametric design, deduced the cycloid tooth profile curve on the coordinate point according to the tooth profile curve of curvature in different distribution density of different formula, and calculated the distribution of the cycloid tooth profile curve of each point on the left and right with the aid of the VC++6.0 program, to provide a theoretical basis for the processing of cycloidal gear.

Key words：optimization of cycloid gear; modification; drawing program verification; parametric design

中图分类号：TH122;TG65

文献标识码：A

作者简介：张跃明(1956—)，男，北京人，北京工业大学副教授，硕士研究生导师，研究方向为RV减速器设计与检测；通讯作者：耿纪玲(1988—)，女，河南信阳市人，北京工业大学硕士研究生，研究方向为RV减速器机构设计，(E-mail)jlgeng@outlook.com。

*基金项目：北京市科技计划项目(D15110400140000)

收稿日期：2015-04-24；修回日期：2015-05-18

文章编号：1001-2265(2016)03-0025-04

DOI:10.13462/j.cnki.mmtamt.2016.03.007