“自动控制原理”课程的工程可视化教学探讨

周 军， 钱惠敏， 任祖华， 孙永辉

(河海大学 能源与电气学院， 江苏 南京 211100)

“自动控制原理”课程的工程可视化教学探讨

周 军， 钱惠敏， 任祖华， 孙永辉

(河海大学 能源与电气学院， 江苏 南京 211100)

本文借助多媒体技术手段，对“自动控制原理”课程的基本概念与数学理论进行可视化教学，培养学生在基本概念形成，数理表达和理论展开以及应用技术融合等方面的能力；促进学生形成理论体系与工程实践融汇贯通的思维；达成在理论教学中培养学生的工程视野和技术素养，使理论与实践教学更好地成为卓越工程师教育培养计划实施的有效途径。

可视化教学；数值仿真；多媒体技术

0 引言

现行国内高等院校的“自动控制原理”课程内容涉及系统论，信息论与控制论中共通的、基础的、围绕工程问题的控制策略探求和实施的理论与技术的知识体系[1～3]。包括系统结构与建模，基本特性(稳定性，瞬态/稳态特性)，及特性解析与综合方法(时域法和频域法)。课程中，大量概念和理论在初创时都有明确的工程技术性，即有基于图形/图像进行表现与理解的本质。然而，随着学科发展，最初的概念与理论被赋予了种种数理解析与数值评价的特征，以致在当前的教学中，概念与理论渐趋抽象，原有图形/图像化的技术表现与理解逐渐淡化甚至消失。与此相伴随的是，概念和理论的数学化讲解占据了课程主导地位，不仅原来工程技术形象逐渐淡化，理论展开与技术实践也渐次分离，技术价值难以从课堂教学中传递给学生。将有关工程技术实践简单地忽视是违背学科发展的，也不被主流学派和先进控制工程技术人员所认同。因此，利用多媒体的图形图像表现技术，构建出既遵从课程数理本质，又形象具体地反映概念和理论的工程技术意义以及实施过程的教学方法，就是自然的考虑[4]。

事实上，“自动控制原理”的众多电子课件都在这方面展开了探索。就笔者所知，目前的课件主要关注于将教师书上的文字型概念与理论表现，通过多媒体转换为屏幕上的电子文字型表现，包括使用图表、算法流程框图等。在这种意义上，多媒体的采用只带来了概念和理论表现的变化，其作用依然是辅助性的。与此相对，如何利用多媒体的表现力优势，将工程问题中的概念提取、基于概念的数学理论展开及其理论结果的工程应用进行全过程的、具象化的关联，做出动态可视化为主导的“自动控制原理”教学课件就是非常值得探讨的了。也就是说，利用仿真软件和多媒体图像图形技术来揭示“自动控制原理”教学内容源于工程，得益于数学支撑与提升，最终回馈应用于工程的知识结构本质，以课程概念与工程技术表现的关联来重构其原有的形象。其作用显然不是辅助性的，而是促使学生自发、自主地在概念形成，控制机理的数理理解，仿真算法及实验技术四者之间建立关联的思维方式，实现理论教学中培养学生的工程师视野和实践能力。为简明起见，“自动控制原理”课程的概念与数理展开的工程意义的可视化教学方案简称为“工程可视化教学”。

1 工程可视化教学示例

本例是围绕行车倒立摆系统(如图1所示)的建模与该模型的平衡控制来完成闭环传递函数零极点与时域响应特性的根轨迹图分析与设计的工程可视化教学。

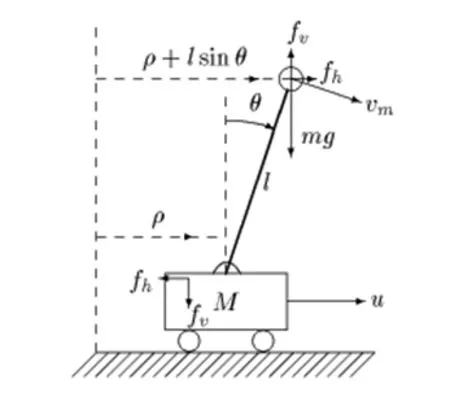
图1 单级行车倒立摆结构

1)系统建模的可视化教学

组织学生接触单级倒立摆平台及其相关测试仪器，教师介绍倒立摆的工程由来与意义；学生观摩基于状态反馈的倒立摆摆杆垂直平衡点控制实验；基于观察向学生提问：系统控制问题的工程特征与目标是什么？其数学表达应该是什么？进而逆溯建模的必要性；在建模教学中，先基于物理定律建立一次理论模型，分析模型基本数学特征，确认模型特征与实验结果的运动学意义的一致性。

建模教学要点。首先，对摆杆顶端质点在铰链为圆心的圆周切线方向上进行受力分析得

(1)

而摆杆关于铰链的运动关系，有

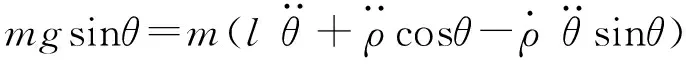
(2)

基于式(1)与式(2)，选择系统状态变量

并考虑以倒立摆的小车推力u作为控制输入量，各状态量均作为测量输出(即反馈量)，则可得到如下非线性微分方程作为对象的原始状态空间模型(一次模型):

(3)

这里x=[x1,x2,x3,x4]T,且

由于式(3)有非线性函数，为此考虑模型简化建立近似模型(或二次模型)。

2)模型简化的实验教学

由学生应用Matlab/Simulink搭建基于一次理论模型的仿真算法，通过数值求解反演倒立摆摆杆平衡点邻域的动态过程，由此判断一次理论模型的有效性和精确性。该环节让学生理解系统仿真是系统建模合理性的检验手段；在课堂教学中讨论简化，变形，变换等将一次模型转换为便于控制设计理论展开的二次模型的技术思想。

模型简化教学要点。在摆杆平衡位置狭小角度内，近似地成立cosθ=1，sinθ=θ，，则式(3)可以在平衡点邻域附近线性化近似为

(4)

归纳起来，分析倒立摆平衡控制问题就可以基于式(4)的线性模型来设定.

3)根轨迹分析

学生借助Matlab /Simulink仿真平台，自主实现出基于位置，速度和摆角，摆角角速度为反馈量的静态控制下倒立摆摆杆垂直平衡控制的仿真实验。先由教师讲解控制器设计思想，给出基于式(4)设计的线性静态反馈控制律，并观察当控制器参数调整时对倒立摆垂直平衡控制效果的影响。

静态增益控制教学要点。基于式(4)引入u=Kx的静态状态反馈，其中反馈增益矩阵为K=[k1k2k3k4]，则闭环特征多项式可以表示为

pc(s)=det(sI4-A-BK)

(5)

若取引入静态状态反馈K后的，期望闭环特征多项式为

(6)

对比被控闭环系统引入K=[k1k2k3k4]的特征多项式，如下参数方程需成立：

(7)

4)平衡控制与控制增益调整的可视化

静态状态反馈K对应的控制作用下的根轨迹图进行分析与观察，可视化地看到当参数增益调整时根轨迹变化和系统动态特性的变化。将状态反馈增益矩阵对应在模型上理解是，利用小车的位置，速度，以及摆杆角度，角速度的反馈形成控制操作u作用到小车上，实现摆杆平衡的控制目标。作为反馈参变量的k1,k2,k3,k4，在仿真实验中是算法系数，在工程实体上可以是放大电路的增益等。

2 结语

本文尝试开展“自动控制原理”课程的工程可视化教学改革，即通过基本概念与数理思想的图形化，静动结合地表现控制工程技术问题与数学概念理论的联系，结合多媒体的交互式教学方法，致力于培养学生的学术理论与工程技术的融会贯通能力，实现创新思维能力和实践动手能力的提高。

[1] 刘文定，谢克明. 自动控制原理[M]，第3版，北京：电子工业出版社，2013.

[2] 周其节，李培豪，高国焱.自动控制原理[M]，第1版，广州：华南理工大学出版社，1989.

[3] K. J. Astrom and R. M. Murray. Feedback Systems: An Introduction for Scientists and Engineers[M], Princeton: Princeton University Press, 2008.

[4] 宫二玲, 孙志强, 沈辉. “自动控制原理”课程中的多元化案例教学[J]. 南京：电气电子教学学报，2015,37(2): 58--60.

Visualization Teaching Approaches for Automatic Control Fundamentals Course

ZHOU Jun, QIAN Hui-min, REN Zu-hua， SUN Yong-hui

(CollegeofEnergyandElectricalEngineering,HohaiUniversity,Nanjing211100,China)

In this paper, visualization techniques are suggested for lecturing concepts and theory of the Automatic Control Fundamentals course. In order to nurture conceptual comprehension, mathematical expansion and application skills for students. visualization is significant in relating their classroom study to engineering practices, which is expected to play a role in acquainting the prominent engineering students with basic engineering experiences and knowledge.

visualization lecturing; numerical simulation；multi-media technique

2015-09-15;

2016-01-14

国家自然科学基金(61573001，61074186)，江苏省自然科学基金(BK20140860)，河海大学教改支撑项目。

周 军(1963-)，男，博士，教授，主要从事控制理论与控制工程的教学和研究，E-mail: jzhouaguar@163.com 钱惠敏(1980-)，女，博士，讲师，主要从事模式识别教学和研究，E-mail: qhmin0316@163.com

G642.0

A

1008-0686(2016)04-0033-03