基于非纠缠直积态的量子密钥分配协议

张德喜

(许昌学院 信息工程学院，河南 许昌 461000)

基于非纠缠直积态的量子密钥分配协议

张德喜

(许昌学院 信息工程学院，河南 许昌 461000)

提出了一个基于非纠缠直积态的量子密钥分配协议.Alice和Bob它们双方通过做局部测量和交换量子位建立起相同的密钥.任何第三者窃取密钥不可能不被发现，所以该协议非常安全.该协议只需要非纠缠直积态，也不需要做复杂的量子操作和集体测量，因此，它非常容易在实际中实现.

量子密码学；量子密钥分配；非纠缠直积态；非局域性

量子密码学是量子物理学在密码学中的应用.它和建立在计算复杂性基础上的经典密码学不同，在量子密码学中，人们利用量子系统的物理性质来保证信息的隐秘性和不可篡改.因此，量子密码协议可以具有无条件的安全性.量子密码学中发展最早和最成熟的是量子密钥分配协议，二十世纪八十年代Bennett和Brassard提出的了第一个量子密钥分配协议[1].随后，人们发展了多种量子密钥分配方案[2-13].当前，量子密钥分配技术已经成功实现了，在距离超过150公里的两个用户之间建立起密钥[14].美国一家公司在2006年已经生产出实用的量子密钥分配器.

文章提出量子密钥分配一种的方法,它利用正交直积量子态.Alice和Bob它们做局部测量和交换量子位建立起共同的密钥.任何第三者窃取密钥不可能不被发现，所以，此协议非常安全.该协议只需要非纠缠直积态，不用纠缠态，不做复杂的量子操作和集体测量，所以此协议在实验室和生产中非常容易实现.

1 基本思想

Bennett等在1999年提出三状态的双量子位系统的直积态也具有某种非局域性[15].

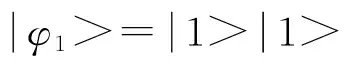
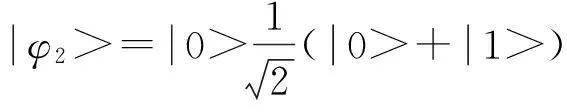
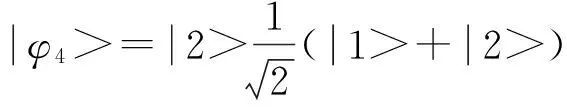
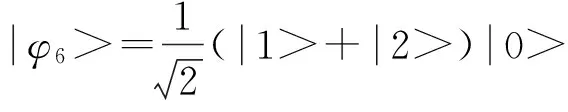
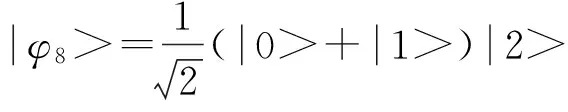
(1)

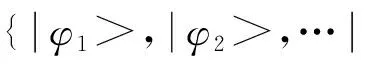
另一方面，Alice按照以下规则发送指令给Bob.

当Bob测量完毕之后，他根据测量结果按照以下规则记录.

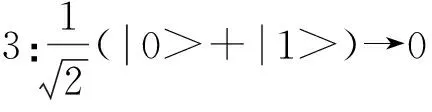
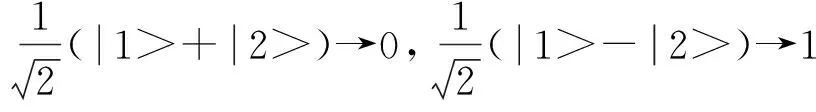
容易看到，Bob得到结果一定和Alice的结果相同，这是Bob和Alice共享的信息，把它作为密钥.后面的内容中，将会证明任何第三者获取密钥都会被Bob和Alice发现.所以，利用前面的方法设计出量子密钥分配协议.

另一方面，Alice发送给Bob的量子位2可能会由于噪声或者攻击者破坏而发生状态改变，这可能会导致双方得不到一致的结果.为了避免这种风险，可以引入检错过程.Alice按照下列规则通知Bob.

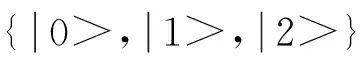
显然，Alice根据双量子位的状态可以准确地预言Bob得到什么测量结果.Bob测量之后，公布自己的测量结果，如果两者一致，说明Bob收到的量子位是正确无误的.

2 基于非纠缠直积态的量子密钥分配协议

量子密钥分配协议具体方法.首先Bob和Alice建立一个它们共享的长度为n的密钥，它们通过两个不同的信道联系，一个是量子信道,另一个是辅助的经典信道.它们可以通过量子信道相互传递量子位，经典信息需要用辅助的经典信道实现它们交换.量子信道是公开的，不同的人都可以监听和控制它；辅助的经典信道是认证的，所有人都可以监听，可是不能控制它.Alice和Bob需要完成以下步骤:

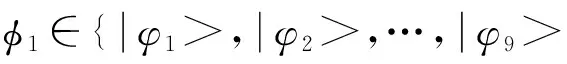
(2)Alice将所有的双量子位系统的量子位2通过量子信道依次发送给Bob.

(4)Alice在余下的双量子位系统中选出n个，然后按照规则2发送指令给Bob，通知Bob测量对应的量子位2.同时，Alice根据双量子位系统的状态序列ψ可以预言Bob的测量结果，并且根据规则3记录下来，最后，她得到一个n位的二进制字符串K1.

(5)Bob按照Alice的指令测量自己手中的量子位2，并且根据规则3记录下来.最后，他也得到一个n位的二进制字符串K2.显然，K1=K2，这就是Bob和Alice共享的密钥.

到此为止，量子密钥具体分配方案已完成.Alice和Bob就可以建立起共同享有的密钥，它们双方就能用这个密钥来具体加密信息.

3 协议的效率和安全性分析

(2)

因此，Alice平均生成一个双量子位系统，贡献密钥的位数为4/9.

另一方面，可以证明，如果它们顺利执行协议完毕，Bob和Alice它们之间就建立共同的密钥，而且没有任何攻击者能够在不被发现的情况下窃取密钥.因此，该协议是非常安全.它们的安全性下面给出具体的证明.

首先，在协议的步骤(5)里，如果没有传输错误和攻击者存在，Alice可以根据双量子位系统的状态序列ψ准确地预知出Bob的测量结果，从而建立双方共享的密钥.而第三者，例如Eve，虽然可以她截获Alice发送给Bob的指令，但是由于Eve不知道状态序列ψ，她无法据此预言Bob的测量结果.因此，她唯一所做的事情只能是仅仅根据Alice的指令来猜测Bob的测量结果.对于每一个双量子位系统，Eve只知道Alice通知Bob选择的测量基，而Bob依据该测量基的测量结果有两种，对应两个码字0或者1，并且两者的概率是相同.所以，Eve恰好猜对的可能性也只有

(3)

最终的密钥有n位，所以Eve恰巧猜对全部密钥的概率为

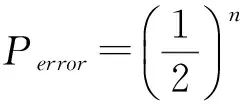
(4)

如果n=100，则:

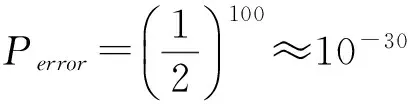
(5)

这是一个非常微小的概率，所以Eve在实际中获得密钥的是不可能.

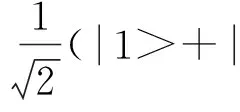
(6)

容易看到，这种情况下，Alice得到的测量结果和Bob推断的结果必定不可能完全一致！详细计算表明，对于每一个双量子位系统来说，两者一致的概率小于1/2.那么，对于t个双量子位系统来说，完全一致的概率，或者说，Eve不被发现的概率为

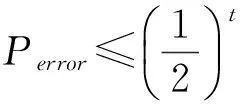
(7)

如果m=1 000，则:

(8)

所以，Eve的存在一定会被Bob和 Alice发现.从而Eve的上述攻击策略注定会失败的.

综上所述，本文的量子密钥分配方案是安全的.

4 结语

上述协议中，协议双方只需要产生和发送处于正交直积态的量子位，然后做简单的定域测量.它既不需要使用纠缠态，也不需要做任何复杂的操作，而且本协议只需要传输量子位序列一次.相对以前的协议具有消耗资源少，可靠性更高的优点.因此，本协议更容易在实践中实现，具有更好的应用价值.

[1] Bennet C H, Brassard G. Quantum cryptography: Public-key distribution and tossing[C].In: Proceedings of IEEE International conference on Computers, Systems and Signal Processing, Bangalore, India, IEEE Press, 1984 : 175.

[2] Ekert A K. Quantum cryptography based on Bell’s theorem[J]. Physical Review Letters, 1991， 67: 661-663.

[3] Nguyen T, Sfaxi M A. Ghernaouti-Hélie S. 802.11i Encryption Key Distribution Using Quantum Cryptography[J]. Journal of Networks,2006, 1(5): 9-20.

[4] Namiki R, Hirano T. Assessment of a quantum phase-gate operation based on nonlinear optics[J]. Physical Review A, 2006, 74(3): 032301.

[5] Qi B, Zhao Y, Ma X F, et al. Quantum key distribution with dual detectors[J]. Physical Review A, 2007, 75(5): 052304.

[6] MatsumotoH R. Multiparty quantum-key-distribution protocol without use of entanglement[J]. Physical Review A， 2007, 76(6): 062316.

[7] Zhao Y, Qi B, Lo H K. Quantum error correction may delay, but also cause, entanglement sudden death[J]. Physical Review A, 2008, 77(5): 052327.

[8] Choi T, Choi M S. Quantum key distribution using quantum Faraday rotators[J]. Journal of Physics: Condensed Matter, 2008, 27: 275242.

[9] Horodecki K, Horodecki M, Horodecki P, et al. Quantum Key Distribution Based on Private States: Unconditional Security Over Untrusted Channels With Zero Quantum Capacity[J]. IEEE Transaction on Information Theory, 2008, 54(6): 2604-2620.

[10] Barrett J, Colbeck R, Kent A. Quantum trade-off coding for bosonic communication[J]. Physical Review A, 2012, 86: 062306.

[11] 赵秋宇，张德喜，李晓宇.利用正交直积态的量子密钥分配协议[J].电子科技大学学报，2008,37(3)：401-403；410.

[12] 张德喜，赵秋宇，李晓宇.利用贝尔测量的高效量子密钥分配协议[J].电子科技大学学报，2006，35(6)：917-919.

[13] ZHANG De-xi,Li xiao-yu.A quantum information hiding scheme using orthogonal product states[J].WSEAS Transactions on computers,2007,6(5):757-762.

[14] Kimura T, Nambu Y. Single-photon interference over 150-km transmission using silica-based integrated-optic interferometers for quantum cryptography[EB/OL]. eprints: quant-ph，2004, 0403104.

[15] Bennett C H, Divicenzo D P , Fuchs C A, et al. Quantum nonlocality without entanglement[J].Physical Review A, 1999, 59: 1070-1091.

[16] Guo G P, Li C F,Shi B S, et al. A novel quantum key distribution scheme with orthogonal product states[J], Physical Review A, 2001, 64: 042301.

责任编辑：赵秋宇

Quantum Key Distribution Protocol based on Untangled Product States

ZHANG De-xi

(SchoolofInformationEngineering,Xuchanguniversity,Xuchang461000,China)

This paper provides a quantum key distribution protocol based on untangled product states. It uses a set two-particle quantum systems in orthogonal product quantum states. The two parties establish the key by exchanging particles and performing the local measurement. No other people can get the key without being found. So the protocol is secure. There are no entangled states and complex quantum operations and collective measurements in the protocol. So it is easier to carry out in practice.

quantum cryptography; quantum key distribution; untangled product states; nonlocality

2015-06-19

基金基目：河南省教育厅自然科学研究项目(2010B520025)

张德喜(1965—),男，河南鲁山人，教授，硕士，研究方向：量子信息.

1671-9824(2016)02-0041-05

TP 309.7

A