基于最小破产概率的最优比例再保险策略
2016-04-14曹玉松
曹玉松
(许昌学院 信息工程学院,河南 许昌 461000)
基于最小破产概率的最优比例再保险策略
曹玉松
(许昌学院 信息工程学院,河南 许昌 461000)
在资本价格服从标准布朗运动的基础上,假定保险公司通过购买比例再保险降低风险,以破产概率最小作为最优衡量标准,构建了相应的Hamilton-Jacobi-Bellman 方程及最优再保险决策模型,通过求解相应的方程,得出了破产概率最小下的最优再保险比例.
布朗运动;Hamilton-Jacobi-Bellman方程;破产概率;比例再保险
再保险是分散风险的一种有效方法,不同目标函数下的最优再保险问题一直是保险研究中的热门问题,这里我们选择破产概率最小作为最优标准.许多学者以效用期望最大化作为最优标准对保险问题进行了大量的研究,Xiao和Yi[1]给出了有限时间内的破产概率的上下界;Young 和 Zhang[2]讨论了基于跳扩散过程的最优投资问题;Promislow和Young[3]讨论了基于比例再保险和投资的破产概率的大小问题;Pergamenshchikov和Zeitouny[4]给出了破产概率的下上界;Azcue和Muler[5]在资本服从Cramer-Lundberg过程的前提下,讨论了最小破产概率问题,其它的结果可以参考Gajek (1979),Daykin (1993), Fleming and Soner (1993)[6-8].与上述文献不同的是本文我们在资本服从布朗运动的前提下,我们采取破产概率最小作为最优衡量标准,通过购买比例再保险来降低风险.基于上述假设我们利用漂移布朗运动和哈密尔顿-雅克比-贝尔曼理论讨论破产概率最小化问题,通过对相应的哈密尔顿-雅克比-贝尔曼方程求解,给出了最优比例再保险决策.论文的安排如下,第一部分,我们建立保费的随机过程,在保费和投资过程服从布朗运动假设下,通过引入再保建立相应的动态模型.本文的主要结论破产概率的最小值以及如何购买比例再保险将在第二部分介绍,第三部分,我们将给出一些相关的说明.
1 模型介绍
根据Promislow and Young (2005),我们通过漂移布朗运动刻画保费过程C如下:
dC(t)=adt-bdW0(t).
(1)
这里,a和b均为正整数,W0(t)为标准布朗运动. 显然,用布朗运动刻画的风险过程是实际情况的一个近似,假设保费以固定的速率c0=(1+θ)a连续支付,这里θ>0为安全系数.设I:I+→I+表示再保险函数,我们假设保险人通过购买比例再保险来降低风险,设Y表示所有的风险,R(Y)表示再保险函数,I(Y)=qY这里q表示再保险的比例.与保费支付给保险公司类似,再保险保费以固定的速率c1=(1+η)aq支付给再保险公司,R(Y)=qY,显然η越大,再保险保费越高,剩余资金越少.
根据(1),剩余过程为
dR(t)=c0dt-dC(t)-c1=(θ-η)adt+b(1-q)dW0(t).
(2)
此外,我们还假设保险人将剩余的资金投到风险市场和无风险市场(银行等)中去以获得最大利润.设S0(t)表示无风险市场的价格过程则:
dS0(t)=r0S0(t)dt,r0>0.
决策α用随机过程0≤q(t)≤1来描述,这里q(t) 表示在t时刻再保险的比例,X(t) 表示将决策α应用到(2)后资金的过程X(t)的动态过程为
dX(t)=[r0X(t)+((θ-ηq(t))a)]dt+b(1-q(t))adW0(t).
(3)
决策α认为是可行的,当满足0≤q(t)≤1. 定义所有的可行决策组成的集合为αs.
2 最小破产概率
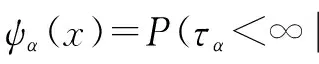
ψ(x)=infα∈αsψα(x).
(4)
我们的目标是得到最小破产概率ψ(x)及其最优的决策q*(t) 使得
ψ(x)=ψq*.
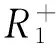
(5)
且边界条件为
ψ(0)=1,ψ(∞)=0.
(6)
下面我们求解带有边界条件(6)的式子(5)的解以及其相应的值函数.
首先我们给出下面引理,该引理在求解式子(5)和(6)中起着重要的作用.
引理1 定义ψ(x)如式子(3). 则:
(7)
相应的最优决策q*=1.

(8)
注意q0(x)<1,若q0(x)≥0 则取q*(x) 等于q0(x), 若q0(x)<0, 令q*(x)=0.
上述讨论过程可得下面两个引理,这两个将在求解方程(5)中用到.
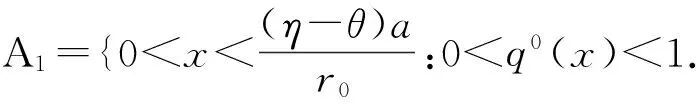
(9)
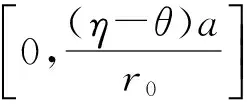
证明 显然,在区间A1上,式子(5)关于变量q的最小值在q0(x) 如式子(8)处取得. 将它们带入到式子(5)可得式(9)的左部.

(10)

由于引理3的证明过程和引理2的证明过程类似,这里我们不再给出其证明过程.
下面我们根据上述两定理求解带有边界条件(6)的式子(5)的解.
设q*(x) 为式子(5)左端取得最小值的决策. 对于q*(x), 这里有两种可能,即 0 若 0 (11) (12) 为了求解带有边界条件(6)的式子(5)的解,引理2 要求式子(12)的q*(x) 在区间(0,1)上, 即 (13) 式子(10)的解为 (14) 这里 (15) 这里常数C2将在随后给出. 根据函数ψ(x)在x=β1处连续,下面我们确定式子(11)中的常数C1和式子(14)中的常数C2.得 (16) (17) 总结上述讨论结果可得如下定理. 定理1 对于边界条件为式子(6)的方程(5)的问题,存在连续可导的函数ψ(x) 及其相应的最优再保险决策如下q*(x): 在资本过程服从布朗运动的前提下,以破产概率最小作为最优衡量标准,通过求解相应的哈密尔顿-雅克比-贝尔曼方程,得出了破产概率最小下的最优再保险比例.然而从保险公司的角度出发,保险人不可能时刻调整自己的决策,但是所得结果在政策改变的任何时刻,都可以作为决策的依据.由于保险公司收取保费后,一般并不需要立刻提供理赔,而是在未来时间,当保险标的发生保险事故后才会理赔,因此保险公司在此期间会将剩余资本投资到风险市场和无风险市场如货币、证券、基金等多个市场开展业务用来增强经济实力,保险在各个市场的资产配置直接影响到公司的收益和风险,如何将资本进行资源分配和利用,如何选择再保险函数的形式,使得风险最小,效用最大,因此基于风险和效用的多目标规划的最优再保险和投资策略是下一步将要讨论的问题. [1] Xiao W, Yi J H. Ruin probabilities for discrete time risk models with stochastic rates for Interest[J]. Statistics and Probability Letters, 2008, 78(6): 707-715. [2] Young H L, Zhang L H, Optimal investment for insurer with jump-diffusion risk process[J]. Insurance Mathematics and Economics, 2005, 37(2):615-634. [3] Young, Promislow D S, Young V R. Minimizing the probability of ruin when claims follow Brownian motion with drift[J].North American Actuarial Journal, 2005, 9(3): 109-128. [4] Pergamenshchikov S, Zeitouny O. Ruin probability in the prensence of risky investments[J]. Stochastic Processes and their Applications, 2006, 116(2): 267-278. [5] Azcue P, Muler N, Optimal investment strategy to minimize the ruin probability of an insurance company under borrowing constraints[J]. Insurance: Mathematics and Economics, 2009,44(1): 26-34. [6] Gajek L, Zagrodny D. Insurer's optimal reinsurance strategies[J]. Insurance: Mathematics and Economics, 2000, 27(3): 105-112. [7] Daykin C D, Pentikainen T, Pesonen M. Practical Risk Theory for Actuaries[M]. London: Chap man&Hall, 1993. [8 ] Fleming H U, Soner H M.Controlled markov processes and viscosity solutions[M]. New York: Springer, 1993. 责任编辑:赵秋宇 Optimal Proportional Reinsurance Strategies Under Minimum Probability of Ruin CAO Yu-song (SchoolofInformationEngineering,XuchangUniversity,Xuchang461000,China) On the basisthat capital price follows standarded Brownian motion, we supposed that a insurance company lowers risk by purchasing proportional reinsurance.The proportion of optimal reinsurance under minimum probability of ruin was gotten by constructing Hamilton-Jacobi-Bellman equation and strategic model of optimal reinsurance under minimum probability of ruin, an optimal measure standard. Brownian motion, Hamilton-Jacobi-Bellman equation, probability of ruin, proportional reinsurance 2015-11-13 河南省科技厅基础与前沿研究计划资助项目(132300410323);河南省高等学校重点科研项目(15A110041);2016许昌市科技局基础与前沿项目 曹玉松(1981—),女,河南濮阳人,副教授,硕士,研究方向:应用概率统计. 1671-9824(2016)02-0028-04 O211.6 A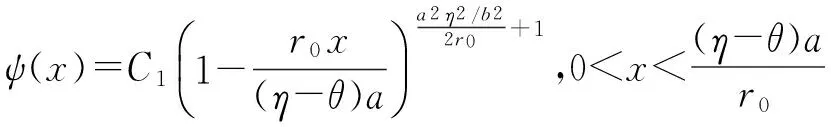


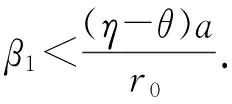
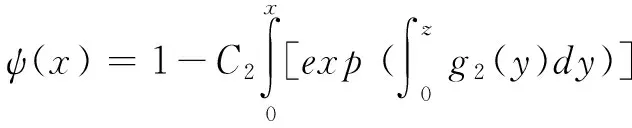
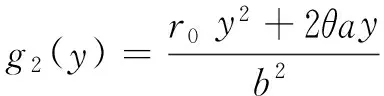

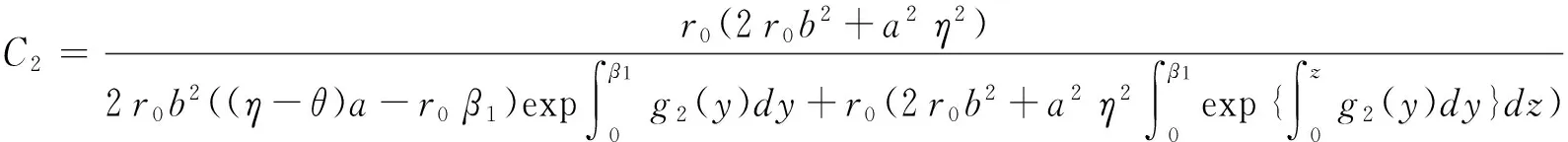
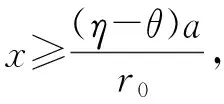

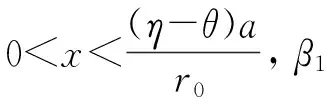
3 结语
