二阶矩阵微分方程通解的按列比较法

吴幼明 ，严意君 ，吴文峰

(1．佛山科学技术学院 数学系，广东 佛山 528000；2．爱荷华威斯莱大学 商业管理系，爱荷华 芒特普莱森特 52641)

二阶矩阵微分方程通解的按列比较法

吴幼明1，严意君1，吴文峰2

(1．佛山科学技术学院 数学系，广东 佛山 528000；2．爱荷华威斯莱大学 商业管理系，爱荷华 芒特普莱森特 52641)

基于矩阵微分方程理论采用按列比较方法，导出了非齐次项为Af″(x)-Bf(x)=t(x)次多项式的一类常系数矩阵微分方程的递推形式通解公式;进行两种特殊情况的讨论，利用算例验证矩阵微分方程通解公式的正确性.

矩阵微分方程；按列比较方法；通解

求矩阵微分方程的通解公式和特解公式[1～5]是微分方程理论的重要内容之一，而对于高阶矩阵微分方程的通解研究，目前研究结果还不够丰富.文献[6]给出了一类三维二阶矩阵微分方程Af″(x)-aAf′(x)-Bf(x)=t(x)的通解公式，但t(x)仅为二次多项式的形式；文献[3～5]分别给出了文献[6]的方程在t(x)为三角函数与指数函数相乘等三种形式的特解公式；文献[7]给出了文献[8]的矩阵微分方程Af″(x)-Bf(x)=t(x)在其t(x)为m次多项式的形式的通解公式.本文在文献[3～8]的基础上，对文献[6]的方程的t(x)改为m次多项式的形式，亦即对文献[7]的矩阵微分方程增加了一阶导数项；采用待定矩阵法和按列比较法，导出了文献[6]的矩阵微分方程在t(x)为m次多项式时的递推形式通解公式，是文献[6]的纵向推广，亦是文献[7]的横向推广，更具一般性.

1 符号

给出矩阵微分方程

(1)

其中fi=fi(x)(i=1，2，3)是关于x的函数，ti(x)(i=1，2，3)是关于x的n次多项式,aij，bij，(i,j=1,2,3)是常数.

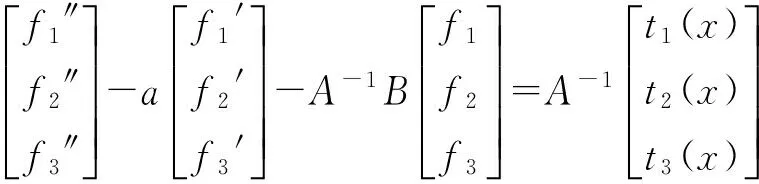
(2)

2 方程的通解

2.1 齐次方程的通解

方程(2)对应的齐次方程为

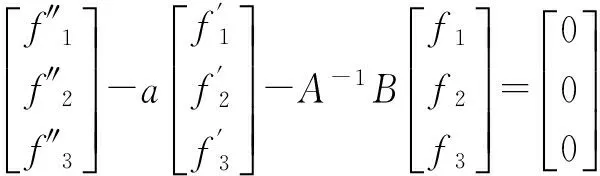
(3)

则方程(3)的通解[6]为

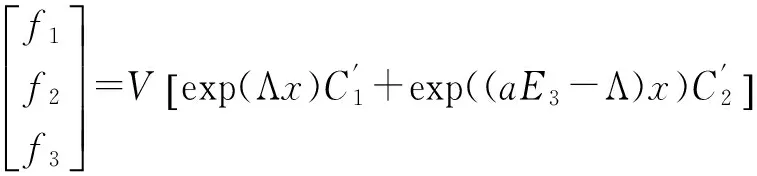
(4)

其中，Λ=diag(λ1,λ3,λ5)；这里

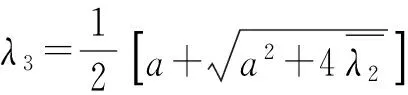
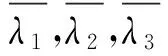
2.2 非齐次方程的通解

给定方程(2)，设

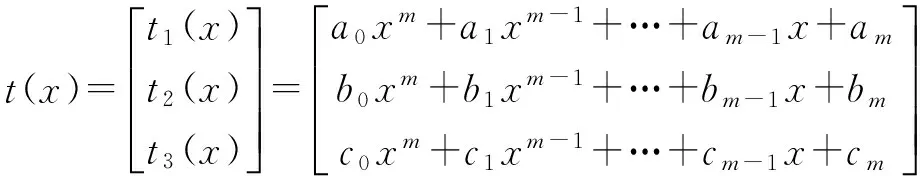
(5)

其中ai,bi,ci(i=0,1,2,…,m)是常数.

根据待定系数法，可设方程(2)的1个特解为

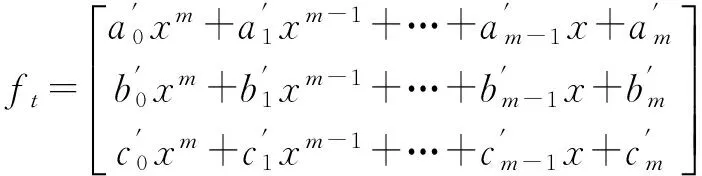
(6)

(7)

比较等式两端x同次幂的系数，得

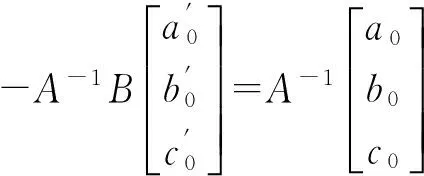
(8)

由式(8)得

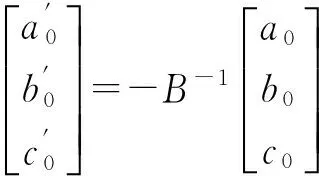
(11)

由式(9)和(11)得

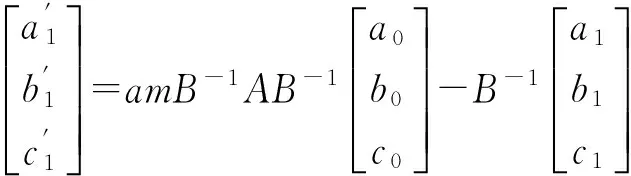
(12)

利用式(11)和(12)的初始数据，由式(10)得递推公式

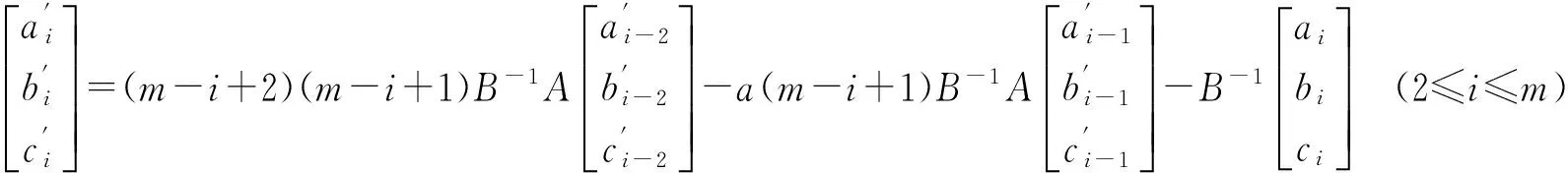
(13)

则方程(2)的一个特解为

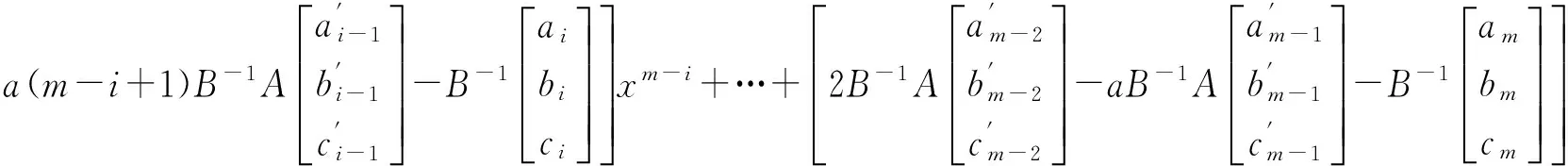
(14)

从而方程(2)的通解为

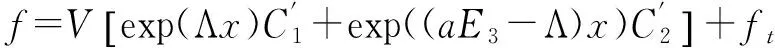
(15)

2.3 特殊情况的讨论

(1)当m=2时，式(14)变为

ft=-B-1t(x)+aB-1AB-1t′(x)-B-1AB-1(E3+a2AB-1)t″(x).

(16)

此结果与文献[6]的结论完全一致，证明本文的通解公式是文献[6]的拓展.

(2)当a=0时，式(14)变为

(17)

此结果与文献[7]的结论完全一致，证明本文的通解公式是文献[7]的推广.

3 算例

用本文方法解下列方程组

(18)

将方程组(18)写成矩阵形式为

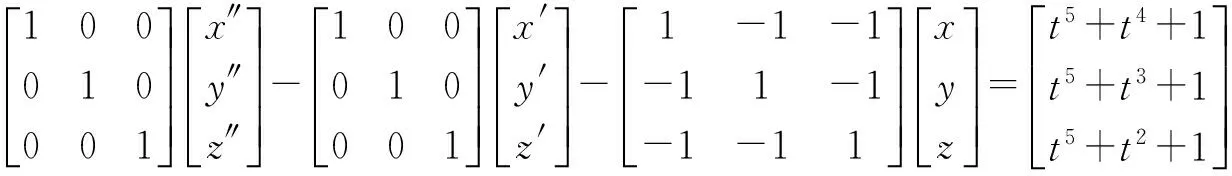
(19)

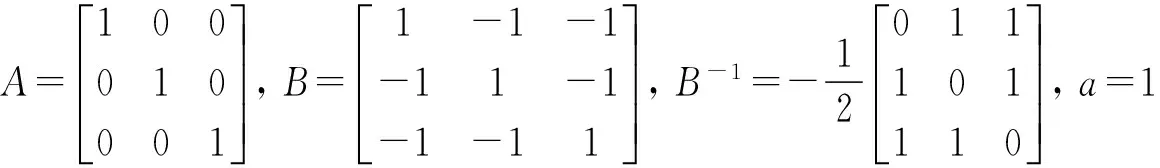
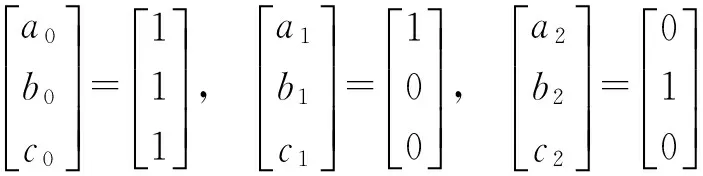
由公式(11)、(12)和(13)得

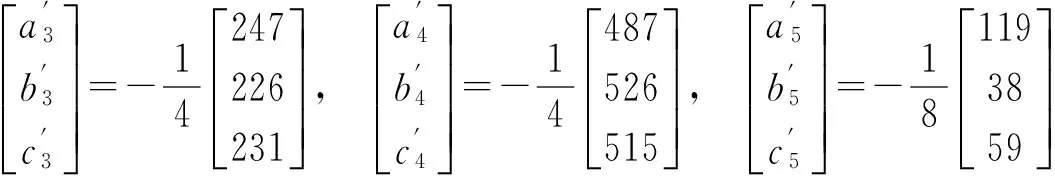
因此，方程组(18)的1个特解为

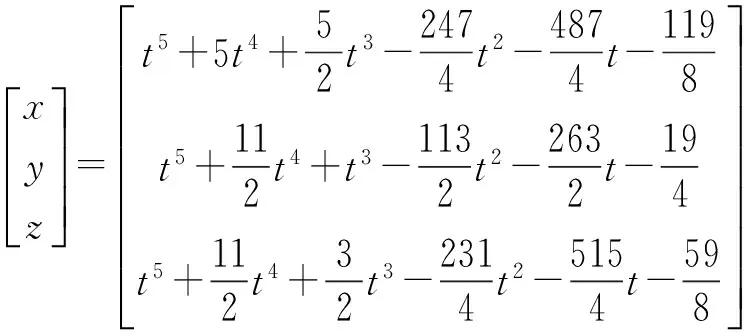
(20)

把特解式(20)代入原方程组式(18)，等式成立.此证明特解式(14)确是方程组(2)的1 个特解.

[1] 化存才.常系数非齐次线性微分方程组特解公式的新推导及其应用[J].云南师范大学学报,2004,24(4)：1-5.

[2] 孙丽强.几种常系数线性非齐次方程组的特解的求法[J].青岛大学师范学院学报, 1997, 14(2)：12-16.

[3] 吴幼明，何佩婷.一类二阶常微分方程组的特解[J].四川理工学院学报,2010, 23(1)：10-13.

[4] 吴幼明，周文苑.一类二阶微分方程组的特解[J].洛阳师范学院学报,2009, 28(2)：1-6.

[5] 吴幼明，周 单.一类二阶常微分方程组的特解[J].佛山科学技术学院学报,2011,29(1)：14-19.

[6] 吴幼明，王向东，岳珠峰.一类二阶微分方程组的通解[J].汕头大学学报,2007,22(3)：15-20.

[7] 吴幼明，陈慧静，陈晓纯，等.微分方程组特解计算的按列比较法[J].佛山科学技术学院学报,2015,33(1)：10-13.

[8] 吴幼明，罗旗帜.一类二阶常系数微分方程组的通解[J].佛山科学技术学院学报,2002,20(2)：10-14.

责任编辑：周 伦

Column Comparison Method for the General Solution of Second-order Matrix Differential Equation

WU You-ming1， YAN Yi-jun1， WU Wen-feng2

(1.DepartmentofMathematics,FoshanScienceandTechnologyUniversity,FoshanGuangdong528000,China; 2.DepartmentofBusinessManagement,IowaWesleyanUniversity,MountPleasant52641,America)

Based on matrix differential equation theory, the column comparison method was adopted to deduce general recursion formula of a type of matrix differential equation with constant coefficients. The non-homogeneous term of the equation isAf″(x)-Bf(x)=t(x) polynomial. Two special cases were discussed in detail and the general formula of matrix differential equation was validated by cases.

matrix differential equation; column comparison method; general solution

2015-10-08

广东省自然科学基金资助项目(S2013010012463)

吴幼明(1962—)，男，广东广州人，副教授，博士，研究方向：应用数学.

1671-9824(2016)02-0024-04

O241.8

A