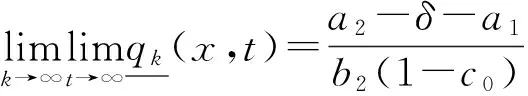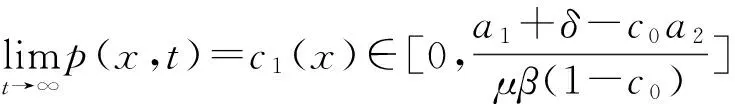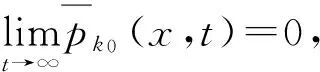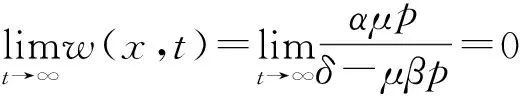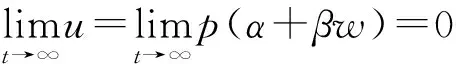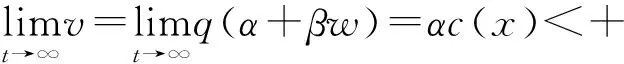一类多种群趋化性模型解的形态研究

陈学勇， 李雪臣

(许昌学院 数学与统计学院，河南 许昌 461000)

一类多种群趋化性模型解的形态研究

陈学勇， 李雪臣

(许昌学院 数学与统计学院，河南 许昌 461000)

研究了一类修正了的多种群Othmer-Stevens趋化性模，利用比较原理、函数变换技巧构造出相应系统的上下解，进而得到了多种群趋化性系统在不同条件下的全局存在、爆破及坍塌现象.

趋化性系统；全局存在；解的爆破；坍塌

趋化性现象是生命系统中普遍存在的重要现象，研究人员不断利用数学建模和试验方法对这一问题进行深入的探讨.自Keller-segel[1]建立了首个经典趋化性数学模型后，由于数学理论上分析的困难及其强大的实际背景使得人们不断对该模型进行修正研究.经典抛物-抛物型趋化性模型得到了充分的研究和发展.当刺激物扩散速度慢时，例如刺激物具有较强黏性的情形，Othmer和Stevens构建了一类Othmer-Steven模型[2].它与经典Keller-Segel模型主要区别在于忽略了化学刺激物的自扩散因素，数学上来看系统变成了抛物-常微组合形式，刺激物扩散项的缺失使得原来处理趋化性模型已有的方式不再适用，特别是高微情形下，非线性和强耦合特性使得系统解的存在和性态结果难以获得.

Sleeman和Levine考虑了一维情形下的模型[3]，他们找到了这一模型的精确解，并且发现在适当条件下解可以全局存在或者在有限时刻爆破.陈学勇，杨茵得到了一类趋化性模型行波解的存在性条件[4].杨茵等讨论了S-L模型在高维下的情形, 并且得到解的全局存在性和爆破的条件[5].

本文中我们讨论如下两个种群并且带有反应项的趋化性模型:

(1)

其中u0(x)>0,v0(x),w0(x)>0∈Cε(Ω)；u表示生物体的浓度或数量；生物体可以是细胞、细菌、昆虫等等；v代表噬菌体的数量、w表示与两种物种有关的化学物质；D1和D2分别代表两个生物种群u,v的扩散系数；Ω是Rn中具有光滑边界∂Ω的有界区域；n表示边界∂Ω的外法向量；Di,ai,bi(i=1,2),μ为非负参量，α,β为正常数；δ>0是化学引诱物的退化率．

趋化性模型是一类强耦合非线性交叉扩散模型，对其研究具有重要的理论和实际意义，本文中利用函数变换技巧、迭代技巧和比较原理得到了关于模型(1)的解的各种性态，巧妙地避开了强耦合交叉扩散带来的分析困难，其结论也印证了生态系统中一些趋化性系统生态变化过程．

方便起见，首先给出一些相关定义．

定义1[5]假设(u(x,t),v(x,t),w(x,t))是模型(1)定义区间[0,T)上的正解， 如果T→+∞, 则称(u(x,t),v(x,t),w(x,t))是模型(1)全局解，否者为局部解.

定义2[5]模型(1)的局部解u(x,t)称为爆破或者坍塌， 如果存在一个有限时刻T>0使得

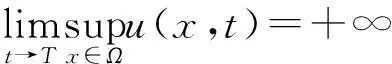
模型(1)的全局解u(x,t)称为最终爆破或者最终坍塌， 如果

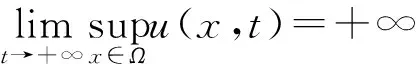
1 函数变换

本节利用函数变换技巧得到系统(1)的等价模型．

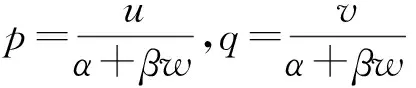
(2)

本文中取D1=D2=1，否则可以利用伸缩变换化成扩散系数为1的情形.

对任意给定的QT上的光滑函数w(x,t)，

(3)

是半线性反映扩散方程的初边值问题，对此问题比较原理是有效的.由抛物型方程理论可知，系统(3)存在唯一的局部解(p(x,t),q(x,t))，它的正则性依赖于初值. 如果p0(x)∈Cε(Ω), 则p(x,t)∈C2+ε,∞(Ω×(0,T)).

为方便起见本文中系统的解指的是满足系统(1)且属于空间C2+ε,∞(Ω×(0,T))的函数，

引理1[1]p(x,t),q(x,t)∈C2+ε,∞(Ω×(0,T))是系统(3)的有界解当且仅当(u(x,t),v(x,t),w(x,t))是系统(1)的有界解，且满足：

我们令

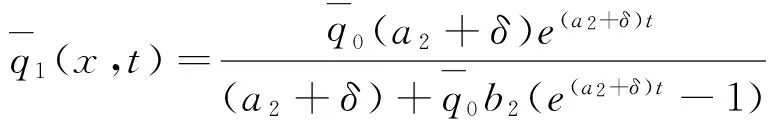
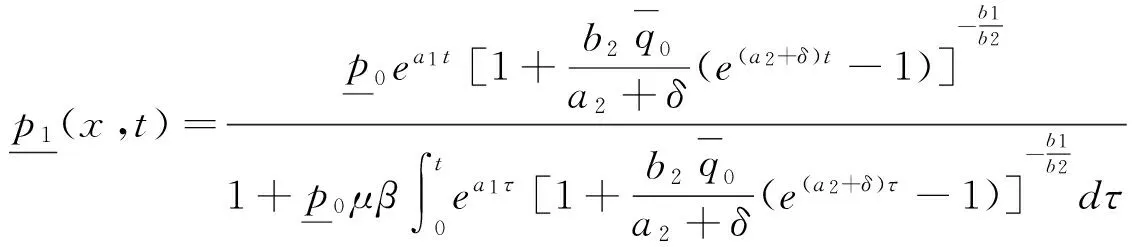
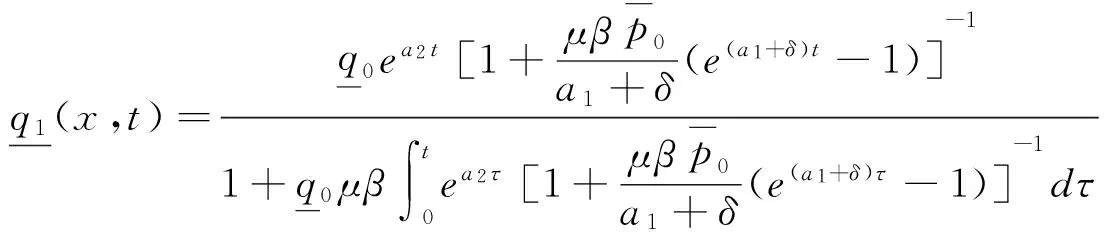
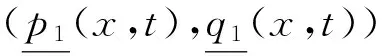
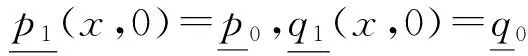
2 解的渐近性态

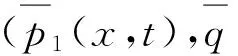
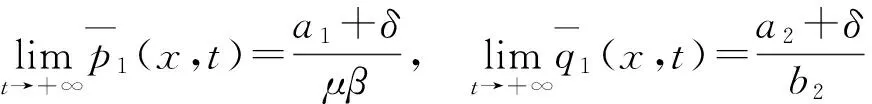
(4)

(5)

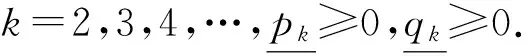
利用比较原理可得如下结论：

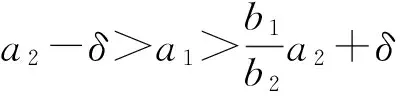
由比较原理，存在

使得

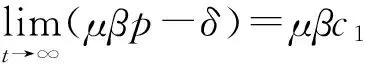
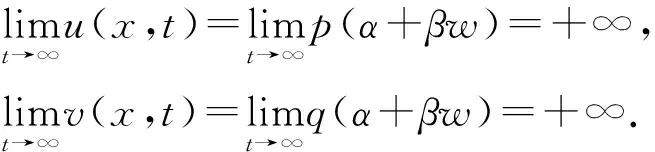
定理1证毕．

注记1 为考察模型的生物意义,u、v、w非负；δ>0表示化学吸引物质w的自我挥发率或损耗率；μ>0表示生物种群u有利于化学物w的增长，例如,生物种群自身分泌的粘液等.

定理2 若参数满足a1>c0(a2+δ),c0≥1,a1≥a2-δ>δ，则系统(1)存在唯一的全局解(u(x,t),v(x,t),w(x,t))，且系统解(u(x,t),v(x,t),w(x,t))最终爆破．

证明 由a1>c0(a2+δ),a1≥a2-δ>δ，可知

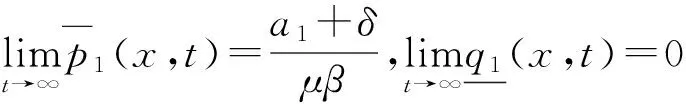
再由a1>δ和w(x,t)的表达式,可以推得

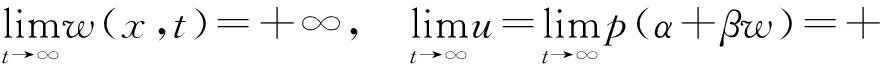
定理2证毕．

定理3 若参数满足a1+δ

(i) 当c0a2-δ

(ii) 当a1+δ-c0a2≤0时，u(x,t),w(x,t)最终坍塌，v(x,t)一致有界．

证明 由a1+δ

又因为c0<1，可知

这意味着w(x,t)一致有界, 进而可知u(x,t),v(x,t)也一致有界.

定理3证毕．

利用定理3中类似的方法可以推得如下结论成立，

定理4 若a1+δ

[1] Keller E F, Segel L A. Initiation of slime mould aggregation viewed as an instability[J]. J Theoret Biol, 1970, 26: 399-415.

[2] Othmer H G, Stevens A. Aggregation, blow-up, and collapse: The ABC’s oftaxis and reinforced random walks[J]. SIAM J Appl Math, 1997, 57: 1044-1081.

[3] Levine H A, Sleeman B D M.Nilsen-Hamilton, Mathematical modeling of the onset of capillary formation initiating angiogenesis[J]. J Math Biol, 2001, 42: 195-238.

[4] 陈学勇，杨 茵.一类趋化性模型行波解的存在性[J].数学学报,2012,55(5):817-828．

[5] Yang Y, Chen H, Liu W A. On existence of global solutions and blow-up to a system of Reaction-Diffusion equations modelling chemotaxis[J]. SIAM J Math Anal, 2001,33:763-785.

[6] Murray J D. Mathematical Biology[M]. Berlin： Springer, 1993.

责任编辑：周 伦

The Behavior of the Solutions to a Multi-group Chemotaxis Model

CHEN Xue-yong, LI Xue-chen

(SchoolofMathematicsandstatistics,XuchangUniversity,Xuchang461000,China)

In this paper, we study a modified multi-group Othmer-Stevens chemotaxis model. By using the methods of comparison principle and function transformation, the sub-supersolution of corresponding system is obtained. Furthermore, we prove the global existence, blow-up and collapse phenomenon of chemotaxis system under different conditions.

chemotaxis system; global existence; blowing up of solution; collapse

2015-12-01

河南省基础与前沿项目(142300410103)； 河南省教育厅基础研究重点项目(15A110042); 许昌市科技局项目(1404003); 许昌学院优秀青年骨干教师资助项目; 许昌学院自然科学重点项目(2015109, 2016078)

陈学勇(1983—)，男，山东泰安人，讲师，博士，研究方向：偏微分方程理论及应用.

1671-9824(2016)02-0009-06

O175.29

A