非线性湿气迁移方程的类Wilson非协调元的超收敛分析

王芬玲，樊明智

(许昌学院 数学与统计学院，河南 许昌 461000)

非线性湿气迁移方程的类Wilson非协调元的超收敛分析

王芬玲，樊明智

(许昌学院 数学与统计学院，河南 许昌 461000)

在半离散格式下研究了非线性湿气迁移方程的类Wilson非协调有限元逼近问题.利用该元的相容误差在能量模意义下可以达到O(h2) 比其插值误差高一阶的特殊性质，并结合协调部分的高精度分析和平均值技巧导出了O(h2)阶的超逼近性，进而运用插值后处理技术得到了超收敛结果.

非线性湿气迁移方程；类Wilson元；超逼近；超收敛

考虑如下的非线性湿气迁移方程[1]

(1)

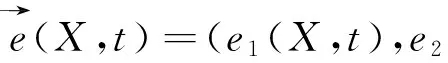
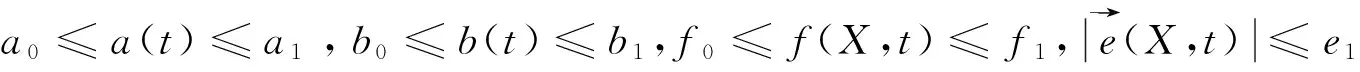
(ii)g(u，X)关于u满足Lipschitz条件.

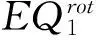
本文将类Wilson非协调元应用于非线性湿气迁移方程，进行了超逼近和超收敛分析.借助于双线性元的高精度分析和类Wilson元的非协调部分与双一次多项式在某种意义下的正交性导出了重要结论(见引理3)，在此基础上，再结合该元的相容误差在能量模意义下可以达到O(h2)阶，利用平均值技巧得到超逼近性.进而，借助于插值后处理技术给出了超收敛结果.

1 类Wilson元构造和重要引理

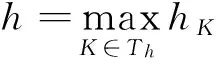
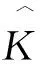
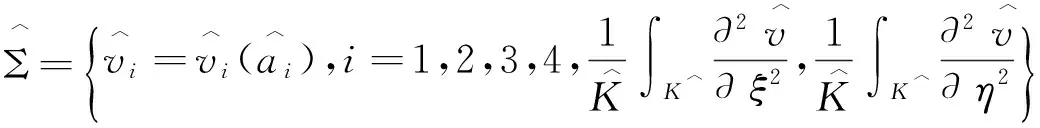
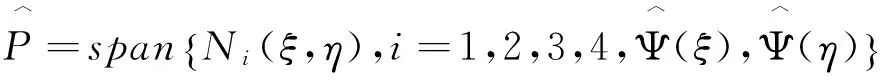
其中

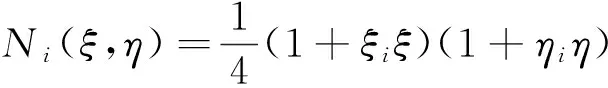
(ξ1,ξ2,ξ3,ξ4)=(-1,1,1,-1),(η1,η2,η3,η4)=(-1,-1,1,1)，

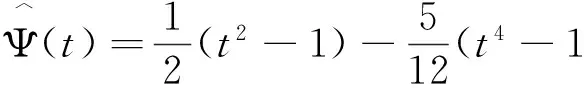
则相应的插值函数为

类Wilson有限元空间可定义为

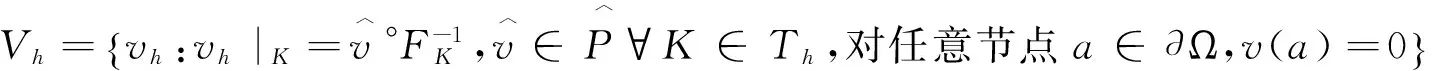
问题(1)的相应变分问题为：

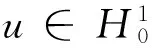
(2)

问题(2)的离散问题为：

求uh∈Vh，使得对任意vh∈Vh满足

(3)

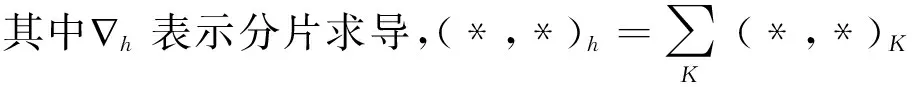
下面给出三个重要的引理.

引理1[8]对任意vh∈Vh，有

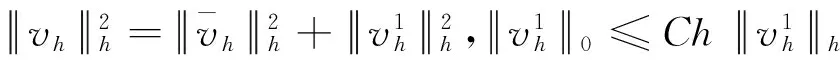
(4)

(5)

其中Q1(K)是双一次多项式空间，C为与h无关的正常数.

引理2[10]令η=u-Ihu，设u∈H3(Ω)，∀vh∈Vh，则有

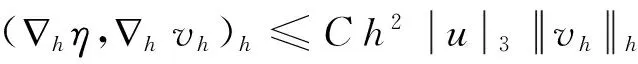
(6)

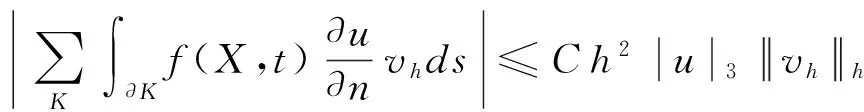
(7)

引理3 设u∈H3(Ω)，∀vh∈Vh，则

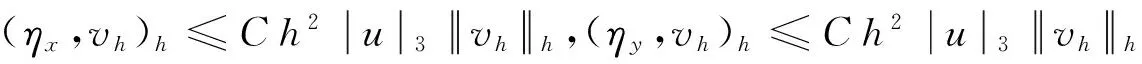
(8)

证明 依据文献[11]有

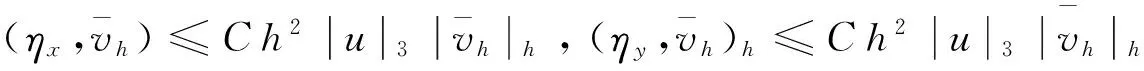
(9)

根据文献[5]得

(10)

由(10)和插值理论得

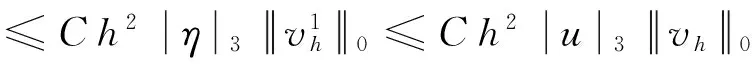
同理有

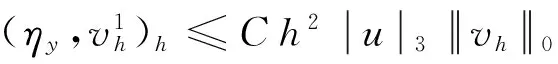
再借助于式(9)，引理3得证.

2 超逼近和超收敛分析`

首先给出超逼近结果.

定理1 设u,uh分别为(2)和(3)的解，u,ut∈H3(Ω)，则

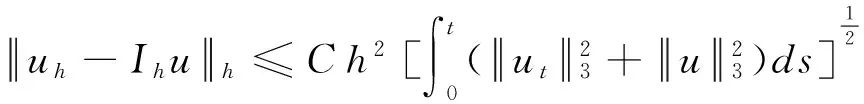
证明 记uh-Ihu=θ，∀vh∈Vh， 由(1)和(3)得

a(t)(hθt,hvh)h+b(t)(θt,vh)h+(f(X,t)hθ,hvh)h

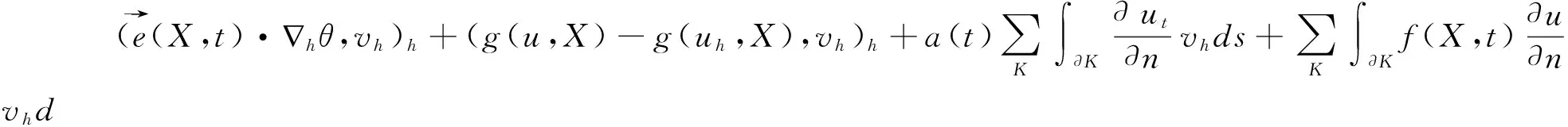
(11)

在(11)中取vh=θt得

(12)

下面对A1～A9逐项进行估计.

根据假设(i)和引理2中的(6)得

由Cauchy-Schwartz不等式和插值理论得

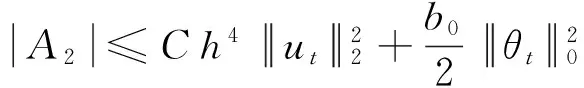
下面的结论在文献[11]中可见

(13)

利用(13)和引理2中的(6)得

根据假设(i)和引理2中的(6)得

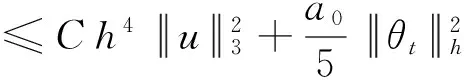
根据(4)得

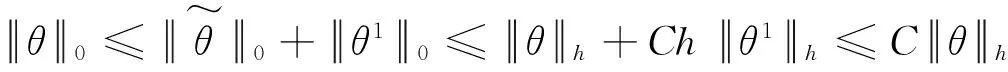
(14)

再借助于(14)和假设条件(ii)得

由假设(i)和插值理论得

根据引理3得

由假设(i)得

(15)

将A1～A9的估计和(15)代入到(12)得

(16)

对(16)的两端从0到t积分，并注意到θ(X,0)=0得

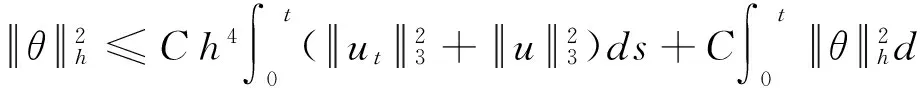
因此，由Gronwall引理得

定理1得证.

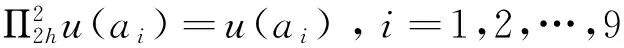
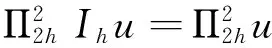
(17)

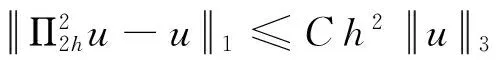
(18)

(19)

定理2 设u,uh分别为(2)和(3)的解，u,ut∈H3(Ω)，则

证明 根据定理1和(17)～(19)得

定理2得证.

[1] 施明德.非线性湿气迁移方程的初边值问题[J].应用数学学报，1990，13(1):31-38.

[2] 陈 宁，李崇新.具Sobolev-Galpern型湿气迁移方程解的渐近性和Blow-up[J].生物数学学报，2002，17(3):305-310.

[3] 涂 慧，刘 超，江成顺.一类二维湿气迁移模型的理论分析及数值模拟[J].信息工程大学学报，2005，6(1):19-22.

[4] 许 超，周家全，张永胜.Sobolev-Galpern型湿气迁移方程各向异性非协调有限元分析[J]. 西北师范大学学报，2011，47(1):34-37.

[5] 裴丽芳，亢金轩，许 超.非线性湿气迁移方程Carey非协调元逼近[J].河南科技大学学报，2011，32(6):81-84.

[6] 江金生,程晓良.二阶问题的一个类Wilson非协调元[J].计算数学,1992,14(3):274-278.

[7] 石东洋,陈绍春.一类改进的Wison任意四边形单元[J].高等学校计算数学学报,1994,16(2):161-167.

[8]ChenSC,ShiDY.Accuracyanalysisforquasi-Wisonelement[J].Acta.Math.Sci.,2000,20(1):44-48.

[9]TaylorRL,BeresfordPJ,WilsonEL.Anonconformelementforstressanalysis[J].IntJNumerMeth.Engrg,1976,10:1211-1219.

[10]ShiDY,WangFL，ZhaoYM.SuperconvergenceanalysisAndextrapolationofquasi-WilsonnonconformingfiniteelementmethodfornonlinearSobolevequations[J].ActaMathematicaeApplicataeSinica,2013,29(2):403-414.

[11] 林 群, 严宁宁.高效有限元构造与分析[M].保定:河北大学出版社,1996.

责任编辑：周 伦

Superconvergence Analysis of Quasi-Wilson Nonconforming Element for Nonlinear Moisture Migration Equation

WANG Fen-ling,FAN Ming-zhi

(SchoolofMathematicsandStatistics，XuchangUniversity，Xuchang461000,China)

Superclose of Quasi-Wilson nonconforming finite element for nonlinear moisture migration equation is discussed under the semi-discrete scheme.By using the special property of the element (the consistency error of which attained O(h2) order in energy model, one order higher than its interpolation error. Combined with high-precision analysis of the conforming part and average value technique), the superclose property of order is derived. Furthermore, the superconvergence result is obtained through the interpolation postprocessing technique.

nonlinear moisture migration equation; Quasi-Wilson element; superclose; superconvergence

2015-11-02

河南省教育厅自然科学基金项目(14A110009)；许昌市科技发展计划项目(1504004)

王芬玲(1968—)，女，河南鄢陵人，教授，硕士，研究方向：有限元方法及其应用.

1671-9824(2016)02-0001-05

O242.21

A