伺服系统速度环参数整定技术的研究*

赵志勇，于　东，王志成,赵鸿博

(1.中国科学院大学，北京　100049；2.中国科学院 沈阳计算技术研究所 高档数控国家工程研究中心，沈阳　110168；3.沈阳高精数控技术有限公司，沈阳　110168)



伺服系统速度环参数整定技术的研究*

赵志勇1，2，于东2，3，王志成2，3,赵鸿博1，2

(1.中国科学院大学，北京100049；2.中国科学院 沈阳计算技术研究所 高档数控国家工程研究中心，沈阳110168；3.沈阳高精数控技术有限公司，沈阳110168)

摘要：为解决伺服系统速度环参数整定这一难题，文中首先提出了一种精确易实现的转动惯量辨识算法;然后根据伺服系统数学模型，利用辨识的转动惯量得到速度环控制器的初步PI参数。考虑到实际系统中不可避免的存在非线性和各种干扰，接着利用遗传算法对计算的PI参数近一步优化,最终得到最优速度控制器参数。理论分析和实验验证了方法的正确性和实用性。

关键词：伺服系统；转动惯量；辨识算法；遗传算法

0引言

永磁同步电动机以其高效率、高功率密度、小转动惯量等优点，在伺服系统中得到广泛的应用[1]。PID算法简单、鲁棒性可靠性高，是伺服系统中应用最广泛的控制方法[2]。伺服系统PID参数的整定是个乏味，耗时的过程且工作环境和对象参数变化后，参数就需要重新校正，因此研究伺服系统PID参数自整定技术具有重要的实践意义。

近些年，一些伺服系统控制器参数自整定技术被提出。文献[3]首先建立伺服系统的数学模型，然后根据经典控制理论将系统整定为最优II型系统，得出整定速度控制器的核心是电机转动惯量的辨识。目前常用的转动惯量辨识方法有加减速法[4-5]，状态观测器法[6-7],模型参考自适应法[8-9]等。其中加减速法原理最简单也最易在伺服系统上实现。文献[4-5]中描述的加减速法一方面忽略了系统摩擦，只能求得转动惯量近似值；另一方面电机要以恒定加速度运动，这在速度环开环条件下很难实现。

文献[3]参数整定方法的正确性是建立在系统精确数学模型的基础上。但实际上为简化分析，必须做一些假设和近似，况且实际控制环境中不可避免的存在非线性、时变和噪声等因素，因此这种方法整定的参数在实际系统中往往差强人意。文献[10]中提出用遗传算法搜索最优PID控制器参数。但是在大范围内盲目搜索不仅造成个体编码长度过长且往往需要迭代很多代。在实现时对数字处理器计算和存储能力要求较高而且寻优的整个过程复杂耗时。

本文提出了一种新的精确的易实施的转动惯量辨识方法并初步整定了PI参数值；然后使用遗传算法对计算的PI值进一步优化；最终得到最优速度环控制器参数。

1伺服系统矢量控制结构

永磁同步电动机的电压，电流，磁通和电磁转矩之间相互耦合，很难分析和控制。为简化电动机模型方便控制，通过矢量变换将三相定子电流分解成互相垂直彼此独立的磁通和励磁电流，然后对其分别调节，实现转矩控制。永磁同步伺服系统矢量控制结构图如图1所示。

图1　伺服系统矢量控制结构图

图中nr,n,θ分别是电机参考转速、实际转速和电机转子位置。伺服系统是复合控制结构，外环是速度环，内环是两个电流环。

电流控制器1调节直轴电流实现电机模型解耦；电流控制器2调节交轴电流以跟随速度调节器输出；速度控制器通过控制交轴电流以控制电机的电磁转矩，从而实现对电机速度的控制。

速度环的控制对象是伺服系统的机械特性，速度控制的参数与电机的机械参数转动惯量有关。但是转动惯量不像电压电流那样可以用仪表直接测量，只能在实验中利用可测的量通过一定的算法辨识出来。

2转动惯量辨识与参数初步整定

2.1转动惯量辨识

加减速法是一种简单易实施的转动惯量离线辨识方法。其主要思想就是让电动机按照某种方式加减速，然后根据电机的机械特性计算出转动惯量。电机的机械特性如下式：

(1)

式中Te，Tl分别是电机电磁转矩和负载转矩，w是电机角速度，B是系统粘滞摩擦系数，J是电机和负载转动惯量和。

在式(1)两边同时乘以电机转速的微分,如式(2)。

(2)

然后两边同时求定积分，得：

(3)

因为加减速的实验往往只需要很短的时间，所以假设在实验期间电机的负载转矩保持恒定。对式求解定积分后得转动惯量的计算公式如下：

J=

(4)

其中t1是实验的开始时间，t2是结束时间；

B和Tl是常数。式(4)的第二部分的值只与实验开始结束时电机的速度有关。因此只要保证t2时刻和t1时刻的转速相等，转动惯量的计算就与Tl和B无关，得转动惯量计算公式如下：

(5)

实验时可以让电机从静止加速到某个速度，然后再让其减速到静止。该过程中既不要求加减速时间相等，也不要求恒定的角加速度。只要记录在此期间的速度和电流信号就可以计算出转动惯量。为方便在数字控制器上实现将式(5)离散化得：

(6)

其中Kt是电磁转矩系数，Iq是交轴电流，Δt是采样周期。

2.2速度环控制器参数初步整定

根据文献[3]电流环可以近似为一个典型的惯性环节。伺服系统速度环控制模型如图2所示。

图2　伺服系统速度环数学模型

图中Ks,Ts是速度控制器的比例系数和积分时间；τ是电流环的时间常数。

系统开环传递函数为：

(7)

(8)

则速度环控制器参数为：

(9)

3速度环控制器参数优化

伺服系统的数学模型是在理想条件下建立的而且在整定PI参数时为方便分析做了一些近似处理，但是实际系统不可避免的存在在非线性、扰动和噪声等因素，因此直接使用式(9)整定参数在实际系统上并不能取得最优的性能，有待进一步优化。

3.1遗传算法基本原理

遗传算法(Genetic Algorithms)是由美国Michigan大学的Holland教授提出的一种模拟自然选择和遗传学机理的并行随机搜索优化方法。遗传算法将参数值编码形成“染色体”，通过遗传中的选择、交叉和变异筛选出适配值高的个体，组成新的群体。这样新的群体既继承了上一带的信息，又优于上一代。通过不断迭代，群体中个体适应度不断提高，直到满足一定的条件。一般遗传算法的流程图如图3所示。

图3　遗传算法流程图

遗传算法具有如下主要优点：①对要寻优的问题形式基本无限制，既可以是显式函数也可以是复杂的系统；②同时适用于单目标和多目标优化；③原理简单，容易在实际系统上实现。考虑到伺服系统结构复杂且要同时求两个参数的最优值，因此选择遗传算法来优化PI参数。

3.2基于遗传算法的PI参数寻优的设计

伺服系统速度环PI参数优化中应用的遗传算法设计包括以下内容：

(1)参数范围和编码方式

利用模型整定的PI参数往往能得到不错的性能，因此可以将搜索范围缩小至按式(9)整定值附近。具体范围可以根据按式(9)整定系统的实际性能而定。

遗传算法中常用的编码方法包括实数编码和二进制编码[11]。二进制编码具有稳定性高、种群多样性大，交叉和变异过程简单容易理解等优点，因此选择二进制编码方式对Kp和Ts进行编码。

解的精度决定了参数编码的位数，精度越高编码位数也就越高，但是计算量就越大。综合考虑控制器的浮点计算能力和控制系统对参数精度的要求，设定求解精度为小数点后3位。为满足这个精度要求，参数编码的二进制位数n要满足式：

2n-1<1000(max-min)<2n

(10)

其中max和min是参数搜索的上下限。

在实际控制系统中需要解码成十进制实数值。因为二进制编码是线性编码，且全0编码对应最小值，全1编码对应最大值，所以解码可以按照公式(11)计算。

(11)

其中b2d()是二进制到十进制转换函数。

(2)初始种群的产生和大小

由于对PI最优参数分布不了解，因此初始种群可以随机生成。比如通过随机函数产生0～1间随机数，输出值落在0～0.5间基因值是0，在0.5～1间基因值是1。

种群越大,其代表性越广泛,最终进化到最优解的可能性越大,但势必造成计算和存储成本的增加。考虑到嵌入式系统的存储和计算能力，选择初始种群个数在10～30之间。

(3)适配函数的选择

适配函数非常重要，往往决定种群中哪些个体被淘汰。适配函数应该和优化问题的目标函数直接相关。对于永磁同步伺服控制系统，目标函数应该能直接反映系统的动态性能。

控制系统常常用误差积分作为系统动态性能综合评价指标[12]。由于实际加工中伺服系统应尽可能快速跟踪速度指令且不能有过大的速度波动，因此采用时间与绝对误差乘积在时间上积分，式(12)，作为优化问题的目标函数。

(12)

其中e(t)是误差信号值，te是一次系统性能测试时间。因为我们是在式(9)整定参数基础上优化，如果测试参数得到的性能还不如初始整定的参数，那么这些个体可以直接抛弃，因此设置te为按式(9)整定的系统的调节时间。

由于系统性能越好目标函数越小，所以遗传算法的适应度函数为：

(13)

(4)选择操作

选择操作采用在遗传算法中最常用的的轮盘赌选择法。在该方法中，各个个体的选择概率和其适应度值成正比例。

假设每个个体的适应度为：

[F(S1),F(S2)...F(Sszie)]

将其按式归一化处理后得每个个体被选中的概率，如式(14)。

(14)

将概率填入轮盘，如图4所示，每次选择时随机转动一下轮盘，当轮盘停止转动时，若指针指向某个个体，则该个体被选中。

很显然具有高适应度的个体更有机会被选中留在下一代，但是由于选择的随机性，选择过程中会丢掉较好的的那些个体，因此设置精英机制，将前代中最优的个体直接选择到下一代中。

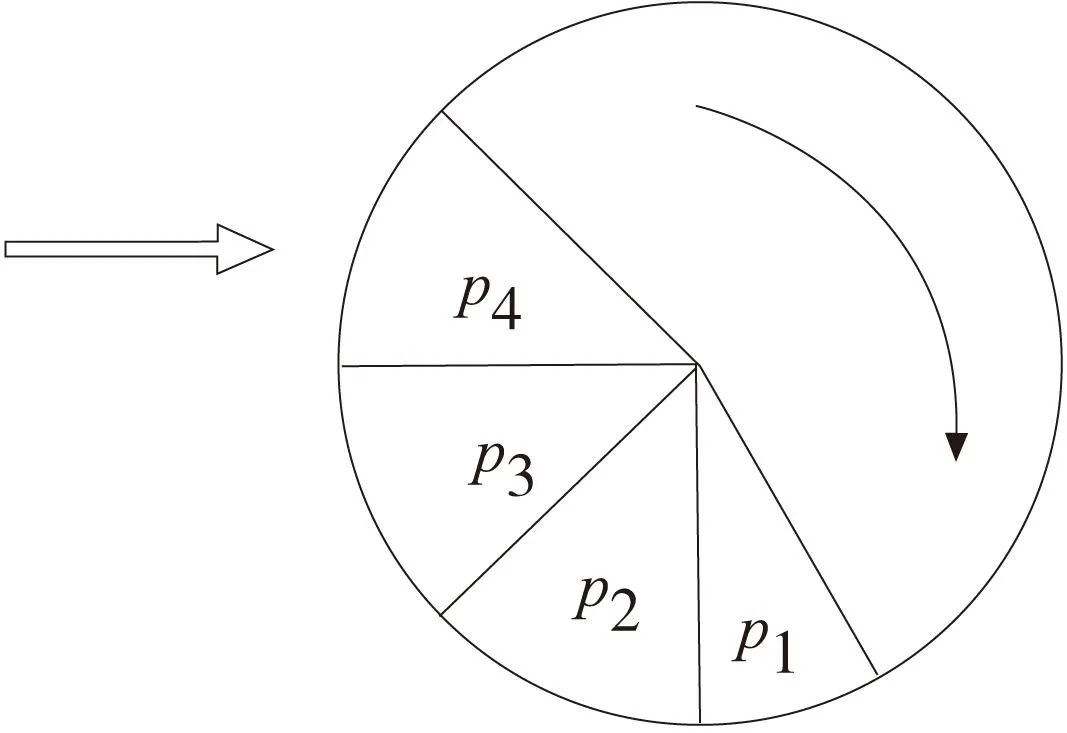
图4　选择轮盘

(5)交叉操作

两个个体的交叉是随机的，交叉概率用Pc表示。Pc过小导致搜索停滞不前;而太大会破坏掉高适配值结构。交叉概率一般在0.25～0.8之间。

二进制编码的染色体交叉过程如图5所示，交叉点的位置可以随机选择。

图5　染色体交叉过程

(6)变异操作

变异操作是模拟遗传过程中基因突变这一小概率事件。为了方便实现，本文采用均匀变异方法，遍历每一个基因判断是否变异。变异概率太大会引起不稳定，变异概率Pm一般为0.001～0.1。

(7)算法终止条件

遗传算法通常的终止条件是最优个体的适应度达到给定的阈值或者迭代次数达到预设的代数。由于无法预测最优系统的性能同时考虑每次迭代的代价，选择迭代的代数为30～50。

综上分析，遗传算法对PI参数寻优流程图如图6所示。

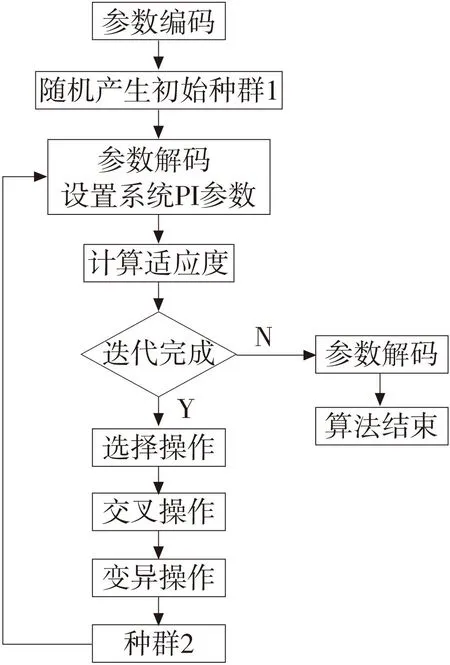
图6　PI参数寻优流程图

4实验与分析

为验证上述转动惯量辨识和寻优算法，以沈阳高精数控有限公司的可重构伺服驱动器为核心，搭建了实际的实验测试平台。实验用永磁交流伺服系统主要性能指标为额定转速为3000r/min;额定转矩为11Nm;电机转动惯量为0.089kgm2。

4.1转动惯量辨识实验

给伺服系统一个速度激励，让电机空载运行一段时间。记录伺服电机从静止加速，然后减速到静止过程中转速和电流信号，如图7、图8所示。

图7　电机交轴电流

图8　电机转速

根据式(6)计算电机的转动惯量为0.0825kgm2,可见辨识算法的正确性和有效性。

4.2参数自整定

在电机带负载情况下，利用上述转动惯量辨识算法初步整定系统PI参数，得系统阶跃响应如图9所示。

图9　初步整定的系统阶跃响应

从图9中可见，系统不仅具有明显的超调，而且收敛到目标值的速度很慢。计算此时系统的ITAE值为0.2073。

选择交叉概率Pc为0.6，变异概率Pm为0.01，让系统迭代40代，每次测试时间为te为50ms,在伺服系统上实现遗传算法。

遗传算法迭代过程中，伺服系统的ITAE值变化如图10所示。由图中可以看出，当系统迭代到30代左右时，系统ITAE值趋于稳定，系统动态性能达到最优。此时系统的ITAE值为0.1056，明显低于初步整定系统的ITAE值。

图10　遗传算法迭代过程

经过优化后的PI参数的系统的阶跃响应如图11所示。

图11　优化后系统阶跃响应

比较图9和图11，优化后系统调节时间明显减小而且具有非常小的超调。

5结论

本文对伺服系统速度环控制器参数整定技术进行了研究。首先提出了一种离线转动惯量辨识方法；然后利用转动惯量初步整定了PI控制器参数；最后利用遗传算法对计算参数近一步优化。理论分析和实验表明：①所提转动惯量辨识算法更加精确实用；②由于利用了初步整定的PI参数值和设置这些值后系统响应信息，遗传算法能更快更准确的找到最优控制器参数。

[参考文献]

[1] 李烨, 严欣严. 永磁同步电动机伺服系统研究现状及应用前景[J]. 微电机, 2001, 34(4): 30-33.

[2] 王伟, 张晶涛, 柴天佑. PID 参数先进整定方法综述[J]. 自动化学报, 2000, 26(3): 347-355.

[3] 仇国庆, 罗宣林, 王平, 等. PMSM 伺服系统的 PID 控制器设计及仿真[J]. 重庆大学学报, 2008, 31(3):259-262.

[4] 杨明,张扬,曹何金生，等. 交流伺服系统控制器参数自整定及优化 [J]. 电机与控制学报, 2010, 14(12):29-34.

[5] 陈鹏展. 交流伺服系统控制参数自整定策略研究[D]. 武汉: 华中科技大学, 2010.

[6] Yang S M, Deng Y J. Observer-based inertial identification for auto-tuning servo motor drives[C]//Industry Applications Conference, 2005. Fourtieth IAS Annual Meeting. Conference Record of the 2005. IEEE, 2005, 2: 968-972.

[7] Awaya I, Kato Y, Miyake I, et al. New motion control with inertia identification function using disturbance observer[C]//Industrial Electronics, Control, Instrumentation, and Automation, 1992. Power Electronics and Motion Control, Proceedings of the 1992 International Conference on. IEEE, 1992: 77-81.

[8] 赵希梅, 郭庆鼎. PMSM 伺服系统的转动惯量辨识和控制器参数优化[J]. 组合机床与自动化加工技术, 2009 (7): 75-77.

[9] 郭宇婕, 黄立培. 交流伺服系统的转动惯量辨识及调节器参数自整定[J]. 清华大学学报: 自然科学版, 2002, 42(9): 1180-1183.

[10] 刘娜, 韩璞. 基于遗传算法的 PID 参数寻优[J]. 计算机仿真, 2002, 19(2): 70-73.

[11] 张晋, 李冬黎. 遗传算法编码机制的比较研究[J]. 中国矿业大学学报, 2002, 31(6): 637-640.

[12] 胡寿松.自动控制原理[M].北京:科学出版社,2007.

(编辑赵蓉)

Research on Parameters Auto-tuning Method of Speed Control Loop for PMSM Servo System

ZHAO Zhi-yong1,2,YU Dong2,3,WANG Zhi-cheng2,3,ZHAO Hong-bo1,2

(1.University of Chinese Academy of Sciences ,Beijing 100049,China;2.National Engineering Research Center For High-End CNC，Shenyang Institute of Computing Technology of Chinese Academy of Sciences, Shenyang 110168,China)

Abstract：To solve the problem of parameters tuning of speed control loop,a novel inertia identification algorithm which is more accurate and easier to implement is proposed.Then the parameters of PI speed controller are tuned preliminary using the identified inertia based on the model of PMSM servo system.Considering non-linearity and disturbance are inevitable in practice,the PI parameters are optimized further utilizing genetic algorithms.Finally,the optimal parameters of speed controller are achieved.The validity and applicability are verified though analysis and experiment.

Key words：servo system;inertia;identification algorithm;genetic algorithms

中图分类号：TH166;TG506

文献标识码：A

作者简介：赵志勇(1991—)，男，河南信阳人，中国科学院大学、中科院沈阳计算技术研究所硕士研究生，研究方向为嵌入式与数控技术，(E-mail)hnsxyzzy@126.com。

*基金项目："高档数控机床与基础制造装备"国家科技重大专项、基于二次开发平台的专用数控系统开发与应用(2013ZX04007-011)

收稿日期：2015-03-18；修回日期：2015-04-09

文章编号：1001-2265(2016)02-0065-05

DOI:10.13462/j.cnki.mmtamt.2016.02.018