摆线针轮行星传动多目标稳健优化设计

迟建华，王承刚，田志涛，李培宏

(1.大连开发区大开产业发展研究中心，辽宁 大连　116600；2.大连运明自动化技术有限公司，辽宁 大连　116600；3.大连机床集团有限责任公司，辽宁 大连　116620)



摆线针轮行星传动多目标稳健优化设计

迟建华1，王承刚2，田志涛2，李培宏3

(1.大连开发区大开产业发展研究中心，辽宁 大连116600；2.大连运明自动化技术有限公司，辽宁 大连116600；3.大连机床集团有限责任公司，辽宁 大连116620)

摘要：采用粒子群优化算法对摆线针轮行星传动进行约束多目标优化设计，求出满足约束条件的Pareto解集。考虑工程实际中误差的客观存在，进行了7因素9水平的均匀试验设计及望目特性的信噪比计算，在此基础上，依据多目标稳健优化设计原理在Pareto解集中选择最稳健的设计做为最终方案。分析了结果方案中目标函数(体积函数和修形误差函数)对各个设计变量的灵敏度，得出了目标函数最为敏感的因素及各因素对目标函数的影响程度用于指导公差的制定和实际加工制造。

关键词：摆线针轮；行星传动；优化设计

0引言

目前，摆线针轮行星传动在国内外都被积极研究发展。文献[1-2]利用普通平面机构的速度瞬心的三心定理，通过针齿上啮合点的位置和坐标变换得到摆线轮的齿廓曲线方程。文献[3]根据曲面单参数的包络方法建立了摆线针轮传动的啮合方程。文献[4]根据微分几何和齿轮啮合原理，由针齿及给定的运动，建立行星轮共轭啮合齿廓的通用方程，并系统分析了摆线针轮啮合传动的特性。文献[5]在对摆线针轮行星传动中摆线轮的修形方式进行分析的基础上，提出了最佳修形齿廓的概念，对采用“负移距+正等距”修形方法获得最佳修形齿廓原理进行了较深入地探讨。有关摆线针轮行星传动单目标优化设计的论文现已多见,虽偶见有双目标优化设计的论文，仍未摆脱传统多目标优化方法的框架。他们的研究成果在不同程度上进一步揭示了摆线针轮行星传动的内在规律，对于提高摆针传动设计质量和加工质量都具有重要的意义。但迄今为止，利用现代优化技术对摆线针轮行星传动进行多目标优化设计的研究尚未见有论文发表。

本文将多目标粒子群优化算法、稳健设计、均匀试验设计及灵敏度分析相结合，通过摆线针轮行星传动算例试图找到一条解决复杂约束、高维且有误差情况下机械传动多目标优化设计的有效途径。

1摆线针轮行星传动的多目标优化设计

1.1多目标粒子群优化技术

摆线针轮行星传动优化设计是同时追求体积最小和修形误差最小的两目标约束优化问题。两目标函数的量纲不同，不能用非现代的加权系数的方法整合成一个目标函数来优化。粒子群优化技术(Particle Swarm Optimization,PSO)在这里得到了成功的应用。文献[6-8]给出了无约束条件下两目标粒子群寻优原则。本文在此基础上，给出了有约束条件下的寻优程序框图如图1所示。该方法是在可行域内先初始化一个粒子群，然后通过优化问题中的各个目标函数来共同指导粒子在可行域内向着各个目标函数不同时增大的方向运行，最终获得非劣最优解集。

图1　寻优程序框图

1.2应用实例

(1)设计原始数据：功率P=30kW，输入转速nH=1500r/min，传动比i=25，摆线轮、针齿销、针齿套、柱销及柱销套均采用轴承钢GCr15，表面硬度60HRC，许用接触应力σHp=1200MPa，针齿销的许用弯曲应力σFp=1200MPa。

(2)选取8个设计变量：

X=[X1,X2,X3,X4,X5,X6,X7,X8]T=

[rp,bc,K1,K2,Δrrp,Δrp,Zp,δ]T

式中：rp—针齿中心圆半径；

bc—摆线轮齿宽；

K1—短幅系数；

K2—针径系数；

Δrrp—正等距修形量；

Δrp—正移距修形量；

Zp—针轮齿数；

δ—转角修形量。

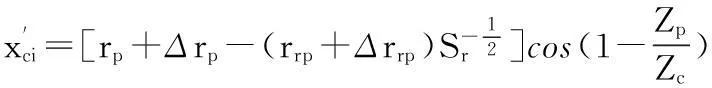
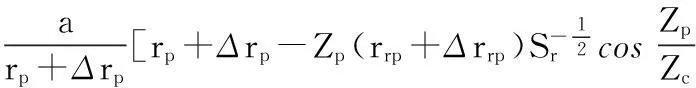
xci—转角修形摆线轮齿形第i个点的坐标

Zc—摆线轮齿数

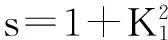
φ—转臂相对于某一针齿中心矢径的转角

a—中心距(偏心距)

(4)确定约束条件：依据文献[9]和工程经验确定齿面接触疲劳强度条件、针齿销抗弯强度条件、刚度条件、限定设计变量的上下界、控制同时啮合有效传力齿数、修形量约束及不产生顶切约束条件。

(5)程序设计：用MATLAB进行程序设计计算，循环100次，结果得到100组可行解及相应的目标函数值。

2稳健设计

采用多目标粒子群优化算法得到非劣解集以后，还必须考虑误差的客观存在，对众多的非劣解采用均匀试验设计计算信噪比，再依据信噪比决策出一组对误差最不敏感的稳健解作为最终方案[10]。

2.1均匀试验设计

均匀试验设计是考虑如何将设计点均匀地散布在试验范围内，使得能用较少的试验点获得最多的信息。

表1　7因素9水平均匀设计表

2.2望目特性的信噪比计算

在实际应用中，望目特性的信噪比按下式计算[10]：

(1)

n—样本点的数量

对于多属性的设计方案，如方案具有[f1(X),f2(X),…fm(X)]m个属性。对m个属性分别求其望目特征的信噪比，得[SN1,SN2,…SNm]，则该方案的信噪比为：

SNA=Min[SN1,SN2,…SNm]

(2)

2.3稳健设计最终方案

信噪比SN*=53.1566

设计变量

X*=[rp,bc,K1,K2,Δrrp,Δrp,Zp,δ]T=

[205.0000,21.4627,0.8049,1.7891,0.4086,0.2083,30.0000,0.0056]T

体积目标函数值：2.8336e+006mm3

结果修形误差目标函数值：0.0105°

3灵敏度分析

式中：m—函数的个数；n—变量的个数。

分别求出目标函数f1(X)和f2(X)在X*处对各设计变量的偏导数：

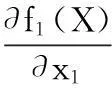
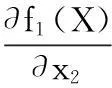
由此可见，总体积目标函数f1(X)随针齿中心圆半径rp和摆线轮齿宽bc单调增加，f1(X)对摆线轮齿宽bc比针齿中心圆半径rp更为敏感。修形误差函数f2(X)对转角修形量δ极为敏感，f2(X)随δ的微小增加而急剧增加。因此，必须严格控制δ的公差，且δ应为负偏差，以使正移距优化组合的齿形曲线与转角修形齿形曲线在工作段上尽量吻合，保证传动的精确性和平稳性。对f2(X)影响次之的因素是短幅系数K1，f2(X)随K1的增加而下降，因此K1应制定正偏差。对f2(X)影响再次之的因素是正移距修形量Δrp，f2(X)随Δrp的增加而单调增加，因此Δrp应制定负偏差。对f2(X)影响最小的因素是针齿中心圆半径rp，其次是针径系数K2。另外还可以看到，f2(X)随正等距修形量Δrrp的增加而单调下降，因此Δrrp应制定正偏差。

4结论

(1)将多目标粒子群优化算法的最优解评估选取原则应用于复杂约束、高维多目标寻优求解中，使得所设计的摆线针轮行星传动即能够总体积最小，又能够修形误差最小，使设计的产品即有较低的经济成本又有较高的加工质量。

(2)从多目标优化结果的非劣解集中选择最终方案时，考虑在生产过程中的误差，首先采用均匀试验设计计算各目标的信噪比，再选择信噪比最大(最稳健)的设计方案作为最终方案。算例验证了采用基于信噪比的多目标决策方法的必要性和有效性。研究还表明，容差越大，非劣解集(备选方案)中真正的可行解越少。因此，为了使设计方案更稳健可靠，可适度取稍大点儿的容差。

(3)通过对摆线针轮行星传动进行灵敏度分析，得到了总体体积和修形误差对各设计变量的敏感程度。对利用灵敏度分析制定公差、指导机械工程实践进行了尝试性工作。

[参考文献]

[1] Shin J H,Kwon S M.On the lobc profile design in a cycloid reducer using instant velocity center[J]. Journal of Mech Theory,2006,41:596-616.

[2] Shin J H,Chang S, Kwon S M,et al.New shape design method of an epicycloidal gear for an epicycloid drive[J].Proceeding of SPIE,2005,6040:60401G1-G6.

[3] Lai T S.Geometric design of roller drive with cylindrical meshing elements[J]. Journal of Mech Theory,2005,40:55-67.

[4] 陈兵奎，房婷婷，李朝阳，等.摆线针轮行星传动共轭啮合理论[J].中国科学E辑：科学技术，2008，38(1)：148-160.

[5] 关天民.摆线针轮行星传动中摆线轮最佳修形量的确定方法[J].中国机械工程，2002，13(10)：811-814.

[6] 魏静萱.解决单目标和多目标优化问题的进化算法[D].西安:西安电子科技大学，2009.

[7] 张敏.约束优化和多目标优化的进化算法研究[D].合肥:中国科学技术大学，2008.

[8] 张利彪，周春光，马铭，等.基于粒子群算法求解多目标优化问题[J].计算机研究与发展，2004，41(7)：1286-1291.

[9] 齿轮手册编委会.齿轮手册[M].北京：机械工业出版社，2005.

[10] 安伟刚.多目标优化方法研究及其工程应用[D].西安:西北工业大学，2005.

[11] 孙志礼，陈良玉.实用机械可靠性设计理论与方法[M].北京：科学出版社，2003.

[12] 张静，张柏林，刘永均.基于灵敏度分析的多学科设计优化解耦方法[J].西南交通大学学报，2007,42(5):563-566.

(编辑赵蓉)

Multi-objective Moderate Optimization in a Cycloid Pin Gear Planetary Drive

CHI Jian-hua1,WANG Cheng-gang2,TIAN Zhi-tao2,LI Pei-hong3

(1.Dalian Development Area Dakai Industrial Development Research Center,Dalian Liaoning 116600,China;Dalian Yunming Auto-Technology Co.，Ltd., Dalian Liaoning 116600,China)

Abstract：We could derive to meet the constraints of the Pareto solution set for cycloid pin gear planetary drive by the particle swarm optimization algorithm for constrained multi-objective optimization. As there is objective error in engineering, on the basis of seven factors, nine levels of uniform design and the look mesh characteristics of SNR calculation,We take the most robust design as the final stage from the Pareto which the multi-objective robust design principle is in. By the analysis of the results of the program in the objective function (volume function and the modification error function) to the sensitivity of the various design variables, it concluded that the most sensitive factors of the objective function and their impact on the objective function which can be used to guide the development of tolerance and the actual processing.

Key words：cycloid pin gear;planetary drive;optimization

中图分类号：TH132.41；TG506

文献标识码：A

作者简介：迟建华(1957—)，男，山东昌邑人，大连开发区大开产业发展研究中心工程师，研究方向为机械设计和工艺，智能制造装备产业区域性发展战略，(E-mail)chijianhua7722@163.com。

收稿日期：2015-12-10

文章编号：1001-2265(2016)02-0033-03

DOI:10.13462/j.cnki.mmtamt.2016.02.010