基于蒙特卡洛法的机器人无碰撞工作空间求解*

付　兵，胡飞飞，陈　琳，潘海鸿

(1.湖北汽车工业学院 机械工程学院 汽车动力传动与电子控制湖北省重点实验室，湖北 十堰　442002；2. 广西大学 机械工程学院 广西制造系统与先进制造技术重点实验室，南宁　530004)



基于蒙特卡洛法的机器人无碰撞工作空间求解*

付兵1，胡飞飞1，陈琳2，潘海鸿2

(1.湖北汽车工业学院 机械工程学院 汽车动力传动与电子控制湖北省重点实验室，湖北 十堰442002；2. 广西大学 机械工程学院 广西制造系统与先进制造技术重点实验室，南宁530004)

摘要：为研究末端执行器对机器人实际工作空间的影响，以及机器人关节之间、末端执行器与机器人关节之间的碰撞对机器人工作空间的影响，文章以6自由度工业机器人为研究对象，研究获取带末端执行器的机器人无碰撞工作空间。提出采用蒙特卡洛法随机生成大量机器人关节转角值，并用这些关节转角值更新机器人虚拟样机的模型位置姿态，然后采取混合包围体层次树碰撞检测算法判断机器人自身关节及末端执行器与机器人关节之间是否发生碰撞来分析机器人的无碰撞工作空间，获取工作空间中的碰撞点，得到机器人的无碰撞工作空间。结果表明本文提出的方法能够有效获取带末端执行器的机器人无碰撞工作空间。

关键词：工业机器人；蒙特卡洛法；工作空间；碰撞检测

0引言

工业机器人广泛应用在装配制造业，尤其在汽车制造行业中，具有广阔的应用前景。机器人工作空间是机器人末端在空间中所达到的位置集合，工作空间的大小代表机器人的活动范围，是机器人的主要性能指标之一，在机器人结构设计[1]、 运动学分析、 轨迹规划及机器人工作站[2]设计中具有重要意义[3-4]。

目前，数值法[5]是获取机器人工作空间最为常用的求解方法，其特点是：不受机器人关节数的限制，是以极值理论和优化方法为基础的，简单且适用于工程问题。Yang X等[6]考虑机器人工作空间中的障碍物对机器人工作空间的影响，提出采用凸超二次曲面包络障碍物和机器人末端执行器，采用内点算法计算机器人与障碍物之间的距离来判断是否发生碰撞从而绘制机器人无碰撞工作空间。田海波等[7]分别采用蒙特卡洛法和定步距角步长法分析机械臂的工作空间，给出机械臂末端的工作空间点云图，证实在分析机械臂的工作空间中，蒙特卡洛法优于定步距角步长法。刘志忠等[8]在机器人工作空间研究分析中，基于蒙特卡洛法获取机器人工作空间的边界点，然后在每个边界点对应的关节变量值的足够小邻域内生成一定数量的新的随机关节变量值，从而得到一些新的工作空间随机点，进而获取更加准确的边界点。李保丰等[9]采用蒙特卡洛法分析三自由度空间机器人的工作空间，得到机器人的工作空间。赵燕江等[10]提出基于Matlab的机器人工作空间求解方法仿真法，利用SimMechanics工具箱，根据机器人的结构进行建模，利用仿真的形式跟踪手臂末端轨迹，并记录其末端点到达的位置坐标，绘制和计算出机器人工作空间。Abdel-Malek K等[11]在研究串联型机械臂的边界曲面时候采用二次曲面获取机器人工作空间，并分析空间中的内、外表面。张鹏程[3]提出采用包络法获取工作空间的包络面方程。

从现有关于机器人工作空间的分析研究中，有学者研究机器人工作空间中的奇异点[12]，有研究除去障碍物的机器人无碰撞工作空间[6]，但目前掌握的文献研究中并没有考虑到：①安装末端执行器对机器人工作空间的影响；②机器人运动中其关节之间以及与末端执行器之间的碰撞问题对机器人工作空间的影响，忽略这两点将导致：①不能获得机器人真正的工作空间；②不能确保机器人自身安全。本文采用蒙特卡洛法和混合包体层次树碰撞检测算法，分析和获取机器人无碰撞的工作空间，这对机器人空间布局优化、末端执行器的设计和选用以及确保机器人安全工作等均有重要意义。

1机器人工作空间计算

1.1机器人正运动学

(1)

(2)

1.2蒙特卡洛法与正运动学

机器人末端参考点可以在机器人坐标系中以机器人关节转角值为变量来表示：

P=(px,py,pz)=fkine(θ1,θ2,…,θN)

(3)

于是，机器人的工作空间可表示为：

(4)

蒙特卡洛法随机生成机器人关节转角值公式如公式(5)所示：

θni=θni,min+(θni,max-θni,min)×tni,tni∈[0,1]

(5)

注：i为机器人关节序号，i=1,2,3,4. . . ；n为随机生成的关节变量组数。

2机器人无碰撞工作空间计算

在机器人各个关节的运动范围中取值时，存在两种碰撞可能：①靠近末端的机器人关节在运动中与靠近底座的关节发生碰撞；②机器人末端执行器在运动中与机器人关节发生碰撞。这两点对机器人在工作空间的运动安全均有影响，实际的机器人安全工作空间应是在排除碰撞点之后工作区间。

为寻找机器人工作空间中的碰撞点，本文借鉴虚拟仿真技术。首先，在三维软件(如Pro/E)建立机器人1：1的三维模型，并将存储格式转换为STL格式(由三角面片组成)；然后编程读取模型文件中三角面片顶点信息，用读取的模型三角面片顶点信息在基于OpenGL建立的虚拟环境中重绘机器人模型以建立机器人虚拟样机；接着，用机器人关节转角值来计算机器人模型当前的位置姿态，并基于混合包围体层次树碰撞检测算法[13]检测该关节转角下模型之间是否发生碰撞，将发生碰撞的机器人关节转角值存储起来；最后，通过机器人正运动学方程将碰撞的关节转角值映射到机器人坐标系中得到取机器人工作空间中的碰撞点坐标。

总体方案流程图如下图1所示，初始化中采用文献[13]的方法建立单个机器人混合包围体层次树。首先，计算机器人各个关节模型以及末端执行器模型的LSS包围体，在LSS包围体的基础上构建AABB包围体作为顶层包围体；然后，在各个关节模型及末端执行器上建立OBB包围体层次树作为中间层，其叶子节点OBB包围体中只包含一个三角面片，并由三角面片组成底层；最后，建立非相邻关节模型碰撞检测对的混合包围体层次遍历树用于检测机器人关节之间的碰撞，建立末端执行器与机器人关节碰撞检测对的混合包围体层次遍历树用于检测末端执行器与机器人关节之间的碰撞。

图1　机器人无碰撞工作空间算法流程图

初始化完成之后采用方程式(5)随机生成机器人关节转角值序列，以该值计算机器人虚拟样机中各个关节模型当前的位置姿态(即三维设计时模型的参考坐标系位置姿态)。如图1中所示，首先根据更新后的模型位置姿态来更新混合包围体层次树中包围体信息；然后在建立的碰撞检测对的混合包围体层次遍历树中进行包围体相交测试，若父节点包围体之间相交则对子节点包围体进行相交测试，直到相交检测到混合包围体层次树底层中三角面片是否相交，若相交则认为该碰撞检测对对应的模型间发生碰撞。如果发生碰撞则将转角值序列存储起来，通过正运动学公式(2)计算得参考点位置坐标值存储到碰撞区域中；不碰撞则通过正运动学公式(2)计算得的参考点位置坐标值存储到机器人工作空间中。重复上述过程直到存储目标坐标点数达到设定点数。对得到的位置坐标点进行绘制得到机器人碰撞区域云图和机器人工作空间云图，机器人工作空间集减去碰撞区域后得到的剩余空间可表示为机器人实际无碰撞工作空间。

3实验及结果分析

工业机器人选用松下TA1400机器人，绘制其三维模型并进行简化，然后基于OpenGL建立机器人TA1400的虚拟样机如图2所示。采用D-H参数坐标法对其进行运动学建模，建模得到机器人D-H参数如表1所示。

图2　TA1400型机器人D-H参数坐标系

Jointθiαiaidi转动范围1θ1-90°1500±170°2θ20°5600-180°-+50°3θ3-90°1300-120-+90°4θ490°0600-180°-+180°5θ5-90°00-90°-+150°6θ60°00-180°-+180°

末端执行器参考坐标系在关节六坐标系中的位置姿态矩阵为:

在基于OpenGL开发的多机器人仿真环境中，采用上述方法求得表示机器人工作空间和碰撞区域的随机点坐标，并进行绘制得到表示机器人工作空间的图3、图4，其中图3为机器人D-H坐标系中关节六坐标系原点P点的云图，图4为机器人末端执行器参考坐标系原点T点的云图；以及表示机器人碰撞区域云图5(末端执行器与机器人关节之间碰撞)、6(机器人关节之间碰撞以及末端执行器与机器人关节之间的碰撞)，图5和图6均为碰撞下T点的云图。图3～图6中四个机器人相对位置是一样的。

由图3、图4可知，安装末端执行器后机器人的工作空间得到扩大，与不安装末端执行器的工作空间形状、体积相比均发生了变化。对应图3、图4中的区域①和②可得原先不能到达的部分点现在可以到达。

由图5得出机器人安装末端执行器后，在其关节转角范围内存在焊枪与机器人关节之间的碰撞区域。由图5和图6云图形状不同且图6中的云图体积大于图5中的云图体积，可得在机器人转角范围内取值时存在机器人自身关节之间的碰撞区域。

由图3、图4与图5、图6对应比较，可以看出机器人的碰撞区域与不碰撞工作空间部分重合。机器人末端工具坐标系存在位置和姿态，本文通过正运动学映射出的点只是工具坐标系的位置，而同一位置不同姿态下，机器人关节组合不同，从而导致相同位置点存在碰撞和不碰撞情形。另外，还可以看出碰撞区域体积小于机器人工作空间体积，那么机器人工作空间集中减去碰撞区域集则可为机器人无碰撞工作空间，该区域内不会发生碰撞。

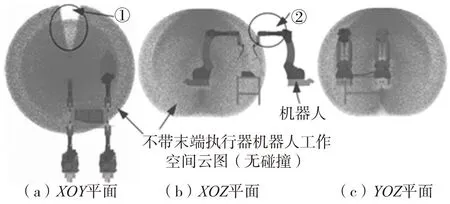
图3　机器人工作空间(P点，50万点)

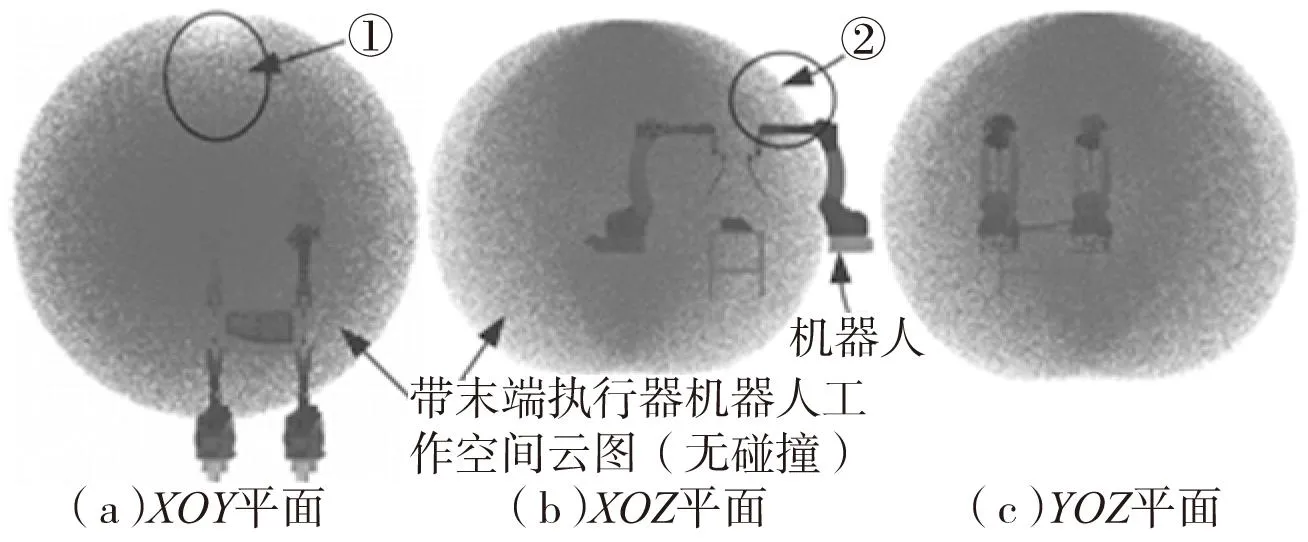
图4　机器人工作空间(T点，50万点)

图5　机器人关节与焊枪的碰撞区域(T点，50万点)

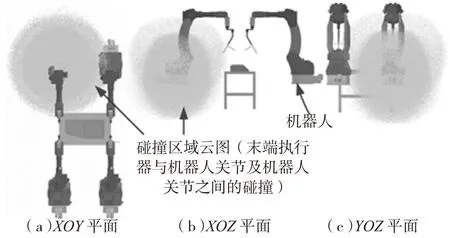
图6　机器人关节之间以及与焊枪的碰撞区域(T点，50万点)

4结论

本文基于蒙特卡洛法和混合包围体碰撞检测算法，采用虚拟现实技术建立机器人碰撞检测模型得到了安装末端执行器后的机器人工作空间中碰撞区域以及无碰撞工作空间，这对机器人结构设计和末端执行器设计、选用以及确保机器人工作安全有重要指导意义，最终可以得到结论如下：

(1)带末端执行器的与不带的机器人工作空间差别较大，末端执行器的选用可以扩大机器人的工作范围。

(2)在机器人关节转角范围内，机器人自身关节之间及末端执行器之间确实存在碰撞区域且与工作空间存在重合部分。基于蒙特卡洛法和混合包围体层次树碰撞检测算法可以有效获取该碰撞区域。机器人工作空间区域减去碰撞区域所得区域即为机器人无碰撞工作空间。

(3)机器人自身关节之间的碰撞区域大于机器人关节与末端执行器之间的碰撞区域，在机器人设计中仅仅限定各个关节的有效转角范围，而不设定各个关节转角范围取值之间的相互约束关系，不能确保机器人运动安全。

[参考文献]

[1] Panda S, Mishra D, Biswal B B. Revolute manipulator workspace optimization: A comparative study[J]. Applied Soft Computing. 2013, 13(2): 899-910.

[2] 王召莉, 陈卫东. 基于关节空间评估的机器人作业单元布局优化[J]. 上海交通大学学报，2009，43(11):1762-1766.

[3] 张鹏程，张铁. 基于包络法六自由度工业机器人工作空间的分析[J].机械设计与制造，2010(10):164-166.

[4] Jin Y, Chen I, Yang G. Workspace evaluation of manipulators through finite-partition of SE(3)[J]. Robotics and Computer-Integrated Manufacturing. 2011, 27(4): 850-859.

[5] Cao Y, Lu K, Li X, et al. Accurate numerical methods for computing 2d and 3d robot workspace[J]. International Journal of Advanced Robotic Systems: INTECH, 2011, 6: 1-13.

[6] Yang X, Wang H, Zhang C, et al. A method for mapping the boundaries of collision-free reachable workspaces[J]. Mechanism and Machine Theory，2010, 45(7): 1024-1033.

[7] 田海波，马宏伟. 井下排爆机器人机械臂运动学及工作空间的分析[J]. 矿山机械，2012，40(9): 105-108.

[8] 刘志忠，柳洪义，罗忠，等. 机器人工作空间求解的蒙特卡洛法改进[J]. 农业机械学报，2013,44(1): 230-235.

[9] 李保丰，孙汉旭，贾庆轩，等. 基于蒙特卡洛法的空间机器人工作空间计算[J]. 航天器工程，2011,20(4): 79-85.

[10] 赵燕江，张永德，姜金刚，等. 基于Matlab的机器人工作空间求解方法[J]. 机械科学与技术，2009,28(12): 1657-1661.

[11] Abdel-Malek K, Yeh H, Othman S. Interior and exterior boundaries to the workspace of mechanical manipulators[J]. Robotics and Computer Integrated Manufacturing, 2000, 16(5): 365-376.

[12] Yang J, Abdel-Malek K, Zhang Y. On the workspace boundary determination of serial manipulators with non-unilateral constraints[J]. Robotics and Computer-Integrated Manufacturing. 2008, 24(1): 60-76.

[13] 陈琳, 付兵, 潘海鸿,等. 一种适用于多机器人的动态包围体层次树碰撞检测算法[J]. 组合机床与自动化加工技术，2014(7):73-76.

(编辑赵蓉)

The Solution of Robot Manipulator’s Collision Free Workspace Based on Monte Carlo Method

FU Bin1, HU Fei-fei1, CHEN Lin2, PAN Hai-hong2

(1.Key Laboratory of Automotive Power Train and Electronics，School of Mechanical Engineering, Hubei University of Automotive Technology, Shiyan Hubei 442002,China;2.Guangxi Key Laboratory of Manufacturing System & Advanced Manufacturing Technology,School of Mechanical Engineering, Guangxi University, Nanning 530004,China)

Abstract：To study the end effector’s influence on actual workspace of the robot manipulator, so at the same time the factors such like the collision between the robot joints, and the collision between end effector and robot joints were take into account to analyze the influence of the robot workspace. This paper makes a research on the collision-free workspace for the robot manipulator with an end effector by using a 6 DOF industrial robot as the object. This paper proposes a method by using the monte carlo method to generate a lot of robot joint angles values randomly, and use those robot joint angles to update the robot virtual prototype’s position and attitude respectively, then use mixed bounding volume hierarchy tree collision detection algorithm to detect the collision among the robot's own joints and the collision between the end effector and robot joints to analyze robot collision-free workspace. In the end, it accesses the collision point in the robot manipulator’s workspace and gets collision-free workspace of the robot manipulator. The results show that the proposed method can effectively get collision-free workspace for the robot manipulator with an end effector.

Key words：industrial robot; monte carlo method; workspace；collision detection

中图分类号：TH166;TG659

文献标识码：A

作者简介：付兵(1987—)，男，湖北广水人，湖北汽车工业学院助理工程师，硕士，研究方向为机器人技术、多机器人协同控制，(E-mail)fubing123456789@126.com；潘海鸿(1966—)，男，南宁人，广西大学教授，博导，博士，研究方向为机器人技术，多机器人协调控制技术，数控，(E-mail)hustphh@163.com。

*基金项目：国家自然科学基金(51065005)；汽车动力传动与电子控制湖北省重点实验室开放基金(ZDK1201408)

收稿日期：2015-09-11;修回日期：2015-10-14

文章编号：1001-2265(2016)02-0016-04

DOI:10.13462/j.cnki.mmtamt.2016.02.005