基于三维高斯束算子解析的方位-反射角道集提取技术研究

蔡杰雄,王华忠,王立歆

(1.同济大学海洋与地球科学学院波现象与反演成像研究组,上海200092;2.中国石油化工股份有限公司石油物探技术研究院,江苏南京211103)



基于三维高斯束算子解析的方位-反射角道集提取技术研究

蔡杰雄1,2,王华忠1,王立歆2

(1.同济大学海洋与地球科学学院波现象与反演成像研究组,上海200092;2.中国石油化工股份有限公司石油物探技术研究院,江苏南京211103)

摘要:通过三维叠前深度偏移提取地下成像点的共方位-反射角(或倾角-方位角)成像道集对于层析速度分析及振幅随角度变化分析(AVA)等至关重要。高斯束叠前深度偏移技术利用相互独立的高斯束描述波传播,并通过相邻高斯束的叠加计算波场,其实现方式解决了多路径问题,且无成像倾角限制。更重要的是,高斯束偏移提供了一种能高精度且方便高效地提取三维共方位-反射角度成像点道集的策略。通过解析求解高斯束算子,计算单个高斯束的波场传播方向矢量,进而通过不同高斯束的传播方向矢量计算得到成像点处的方位-反射角,从而实现三维高斯束叠前深度偏移方位-反射角成像道集的提取。数值计算及实际数据应用结果证明了三维高斯束叠前深度偏移共方位-反射角道集提取技术的有效性。

关键词：方位-反射角道集;高斯束偏移;射线追踪

目前工业界在进行层析速度分析时所输入的成像道集主要是利用Kirchhoff叠前深度偏移技术提取的偏移距域共成像点道集(ODCIGs),但Kirchhoff偏移所利用的偏移距参数是定义在数据面(地表)的炮检点距离而非地下成像点的信息。在复杂构造区,由于忽略了不同偏移距矢量对应不同方位的波传播,且基于单程旅行时的Kirchhoff偏移无法准确描述多路径,从而导致成像质量不佳,成像道集产生假象;而通过计算成像点处的方位-反射角进而提取共方位-反射角成像道集可以避免偏移距域成像道集的这些缺陷。另外,方位-反射角成像道集为AVA分析提供了更可靠的输入。对于射线层析速度分析,方位-反射角道集提供了地下成像点的初始射线追踪方向,使得层析速度分析向地表实施射线追踪的过程相较于偏移距域更加自然和有效。

诸多学者研究了提取地下成像点处的角度域成像道集(ADCIGs)技术[1-18]。角度域成像道集可以通过Kirchhoff叠前深度偏移[15]及高斯束偏移[19-26]等射线类偏移方法获得,也可通过波动方程偏移[10-12,14,18]和逆时偏移[17]等波动类偏移方法获得。但通过波动类偏移方法提取三维地震数据的方位-反射角度道集的计算代价相当大,因此其在工业界中并没有得到大规模的应用。考虑到射线类偏移方法在提取方位-反射角度道集上相对容易和代价较小,我们利用高斯束叠前深度偏移技术提取地下局部方位-反射角道集。

高斯束叠前深度偏移是一种精度较高、灵活高效的偏移技术,可以对陡构造成像,且容易扩展应用于起伏地表和各向异性介质。国内外针对高斯束偏移实用化提取方位-反射角道集的研究较少,GRAY[13]指出高斯束偏移可以提取偏移距域道集,也可以提取角度道集,并与Kirchhoff偏移提取角度道集相对比：高斯束偏移由于计算的走时场相对光滑,使得在求取射线传播方向矢量时更加稳健而更有利于提取三维方位-反射角道集,但并未给出如何定义三维方位-反射角及如何解析地高效提取角度道集。本文中,我们通过解析计算单个有限空间范围内的高斯束旅行时梯度得到波场传播方向矢量,进而通过不同高斯束的传播方向的矢量代数运算得到成像点处的方位-反射角从而提取方位-反射角道集。相比于波动类偏移方法需要复杂的映射变换计算方位-反射角度,高斯束偏移方法解析地求解高斯束函数,实现方式更加方便和高效。同时,由于射线束是一种基于射线理论描述特征波场的波传播方式,既保留了射线的灵活性又兼顾了波传播的精度。射线束局部波传播的特点有利于提取地震数据局部波场特征,这种对特征波场选择性表达的特点使其对山前带低信噪比数据适应能力更强。

1方位-反射角定义

计算地下成像点的方位-反射角的一种有效且高效的方法是分别估算从炮点和检波点出发到达成像点处的波场传播方向。一旦获得两者的传播方向,即可通过向量的代数运算得到方位角和反射角(张角)。对于射线类偏移方法而言,这个过程相对简单和容易,只需通过旅行时场的空间导数分别计算震源射线慢度ps和检波点慢度pr。如图1所示,方位角φ和反射张角θ可以通过如下的向量代数运算得到:

(1)

(2)

其中,psr=ps-pr,x=(1,0,0),y=(0,1,0),z=(0,0,1)。

公式(1)中的反射张角θ定义为反射角α的两倍。公式(2)表示的方位角φ是相对于参考方向单位矢量x而言的。在本文中,我们定义参考方向沿着坐标轴x正方向(图1,从炮点S出发和从检波点G出发到达成像点R处的射线慢度矢量分别表示为ps和pr。通过在成像点附近的局部空间中定义方位角(旋转角)和反射角(张角)),而方位角φ对应的几何意义是局部炮检点方向矢量psr在水平面x-y上的投影沿着x轴逆时针方向的旋转角。这里,我们认为方位角的参考方向固定不变,如本文中的x轴方向(正东方向,当然也可以选择y轴方向,即正北方向为参考方向),该方向不随局部反射平面[ps,pr]的变化而变化。

图1　定义地下成像点的方位-反射角

2方位-反射角道集高斯束偏移

高斯束是波动方程集中于射线附近的高频渐近解。射线中心坐标系中的高斯束波传播类似于球面波传播沿着一个特定的波矢量在局部点进行傍轴近似展开,其数学实质就是沿射线中心坐标系进行傍轴近似方程的波传播。高斯束偏移就是利用高斯束近似描述波传播并利用一定的成像条件进行成像。因此,单个高斯束是高斯束偏移中描述波传播的最小单位。

2.1高斯束算子

利用三维频率域高斯束函数[25-26]在射线中心坐标系中表达波动方程：

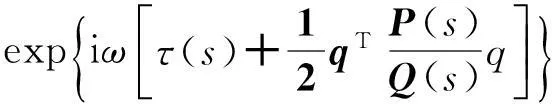
(3)

式中：ω表示圆频率;v(s)和τ(s)分别代表中心射线的速度和旅行时;qT=(q1,q2),其中q1,q2是射线中心坐标系中垂直于中心射线的两个坐标分量;矩阵P(s)和Q(s)是一个2×2的复数矩阵,沿着中心射线通过动力学射线追踪方程求解得到,表征动力学射线追踪参量,如(4)式所示,其决定了高斯束传播的宽度及波前曲率。

(4)

式中:V(s)是一个2×2矩阵,表示速度沿着射线中心坐标q1,q2的二阶偏导,即：

(5)

i,j=1,2

为了求解方程组(4),HILL[26]给出了合适的初始值以保证高斯束传播不存在波场的奇异性区域。

图2是根据公式(3)和公式(4)计算得到的一个常速介质下传播的高斯束。红色射线代表其中心射线,蓝色线圈定了该高斯束传播的有效范围,即下一步求解高斯束波前慢度矢量限定在该有效范围内。

图2　根据公式(3)和公式(4)计算的单个高斯束传播示意图解

2.2高斯束算子解析计算慢度矢量

单个独立的高斯束分两步求得,即通过运动学射线追踪求取中心射线的路径及旅行时,通过动力学射线追踪获取中心射线附近的高频能量分布。利用相互独立的高斯束描述波传播,既保持了射线方法的高效性和灵活性,又考虑了波场的动力学特征。

根据公式(3)所示的高斯束函数,可以解析得到高斯束有效范围内任意一点的旅行时。如图3所示,假设中心射线附近任意一点Q,其对应的中心射线上的点R,则点Q的旅行时可以由点R的旅行时及动力学射线追踪参量表示为：

(6)

其中,

(7)

(8)

k=1,2,3

从(8)式可以发现,因计算方位-反射角度而增加的计算量很小。其中,矩阵M和射线中心坐标q1,q2及其导数分别在高斯束偏移的射线追踪过程中得到,其本身与计算角度道集无直接关系,增加的计算量仅仅是计算慢度矢量((8)式)和计算方位角((1)式)及反射角((2)式)本身。定量分析高斯束偏移与提取三维共方位-反射角成像点道集的效率对比将在理论模型测试中给出。

图3　三维射线中心坐标系

值得注意的是,高斯束函数所描述的光滑旅行时场使得其相较于单程旅行时的Kirchhoff偏移能提供更为稳健的角度域成像道集。在速度模型较简单时，由于无多路径问题,Kirchhoff偏移所计算的旅行时场表现为比较稳定光滑,这时可利用其旅行时场的空间导数计算波场传播的慢度矢量,从而利用相似的方式提取方位-反射角道集;但当速度模型较为复杂时,基于单程旅行时的Kirchhoff偏移所计算的旅行时场常常存在突变点,使得利用其空间导数计算射线的慢度矢量的方式变得困难,进而提取的共方位-反射角成像道集亦不可信。

2.3压制噪声的高斯束偏移

从方法上讲,高斯束偏移主要包括运动学、动力学射线追踪及高斯束波场延拓两个部分。而高斯束偏移将格林函数分解为一系列对计算点有贡献的高斯束,其实现过程就是对计算点有贡献的高斯束的叠加,表达式为：

(9)

(9)式所表示的格林函数代表地下任意一点x′=(x′,y′,z′)的最终波场值是由相邻若干个相互独立的高斯束在该点的积分得到,通过相互叠加的策略可以避免复杂介质引起的波场多波至问题。uGB表示从震源点x=(x,y,z)出发的单个高斯束在目标点x′=(x′,y′,z′)的高斯束波场,即(3)式。

在叠前偏移中,需要分别从炮点及接收点进行射线追踪以求得从炮点出发的下行波和从反射点出发到达检波器的上行波。类似于波动方程偏移,所使用的成像条件是上行波场和下行波场的互相关：

(10)

式中：G(x,xs,ω)与G(x,xr,ω)分别表示从炮点到成像点以及从成像点到检波点的格林函数;“*”代表共轭;Ds(xs,xr,ω)表示基于炮道集输入进行的局部平面波分解,即线性局部τ-p变换,如(11)式,每一个平面波分量对应着下延的一个高斯束。

(11)

式中：f(t,x)代表输入炮道集数据,积分范围x1与x2确定了局部τ-p变换的输入范围;p代表变换后的平面波分量的方向,同时也确定了该平面波分量对应的高斯束初始入射角度。

高斯束偏移利用局部倾斜叠加将原始炮道集数据分解为局部平面波数据,然后对每个局部平面波数据利用其初始入射角所确定的高斯束进行延拓并成像。局部倾斜叠加在得到平面波数据的同时也压制了原始数据的随机噪声,提高了数据信噪比。

进一步考虑对高斯束传播进行“优选”,可以利用相似系数((12)式)在τ-p变换时判断输入数据局部同相轴的相似程度,从而在高斯束延拓成像时区分该平面波数据是“噪声”还是“信号”,仅对“信号”进行高斯束延拓成像可以明显提高高斯束成像的信噪比。

(12)

实际处理时,根据实际数据具体情况可以对相似系数设置一个阈值,只有相似系数大于该阈值的平面波分量才被认为是“信号”而参与高斯束延拓及成像。对原始数据在局部平面波分解时进行相似系数筛选使得高斯束偏移技术相对于其它偏移技术可以明显提高成像信噪比,这一优点在低信噪比数据的成像处理中尤为重要。

3理论模型及实际数据应用

为了验证本文所述的高斯束叠前深度偏移提取方位-反射角成像道集技术的有效性,我们进行了理论模型和实际数据的测试验证。

3.1理论模型测试

首先选择了二维Sigsbee2A数据,以测试该方法在二维情况下提取反射角(无方位角)道集是否正确。从图4可以看出,Sigsbee2A速度模型的特点包括多个薄层、两排点绕射以及盐下陡构造成像,而高斯束叠前深度偏移结果显示出良好的适应性,薄层分辨率较高,绕射点收敛,特别是陡构造成像界面清楚。

从图4可以看出,高斯束偏移在真速度模型下可以提取得到较高质量的角度道集,即使在断层及绕射点处的分辨率依然较高,并且整个成像道集得到很好的拉平,验证了算法的正确性。

前面提到了高斯束偏移输出角度道集所增加的计算量很小,为此,我们在该理论模型上做了测试,对比高斯束偏移仅输出偏移剖面不输出角度道集与输出角度道集的效率对比,所测试的计算机环境(表1)及测试参数完全相同,具体测试结果见表2。

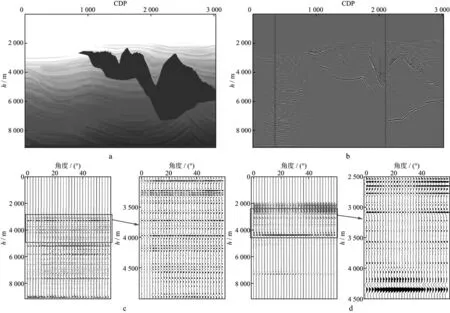
图4　Sigsbee 2A模型高斯束叠前深度偏移剖面及提取的两个CDP位置的角度道集a Sigsbee2A层速度模型; b 高斯束偏移剖面(红线代表将提取角度道集的位置); c CDP400处的角度道集(角度为0～60°,角度间隔2°); d CDP2 100处的角度道集(角度为0～60°,角度间隔2°)

硬件环境①处理器:Intel(R)Xeon(R)X5650②处理器主频:2.66GHz③物理内存:48GB④每个节点CPU数:2个(每个CPU6核)软件环境①操作系统:RedHatEnterpiseLinux4-64Update5②并行计算环境:MPICH1.2.6③编译器:INTELC++、FORTRAN编译器10.0.023Linux版(64位)④配置英特尔MKL9.1(MathKernelLibraryClusterEdition)数据库网络环境1000M,4GB光纤

表2　高斯束偏移仅输出剖面与输出角度道集的效率对比

注：Sigsbee2A模型数据共500炮，数据量909M，共152684道。在完全相同的机器环境条件下分别利用50个节点进行处理。

为了验证三维情况下提取方位-反射角成像道集,我们设计了一个包含两个水平反射层的简单理论模型(图5a),在此模型上正演全方位角数据,其观测系统如图5b所示,炮点位于观测中心。图5c显示了位于模型中心位置成像点的方位-反射角道集，该道集将方位分为8个,间隔45°,而提取的反射张角范围是0～60°,可以看出,从该模型提取的方位-反射角道集按不同方位和反射角准确地排列,验证了本文方法的准确性。

图5　三维全方位观测系统正演数据高斯束偏移提取方位-反射角道集a 三维水平反射界面模型; b 单炮全方位观测系统设计; c高斯束叠前深度偏移提取的方位-反射角道集(方位角分成8个,反射张角范围为0～60°,间隔2°)

3.2实际应用分析

图6展示了一个中国南方实际数据应用高斯束叠前深度偏移提取方位-反射角道集的应用实例。图6a为某条inline线单程波叠前深度偏移剖面;图6b为相同inline线高斯束叠前深度偏移剖面,剖面上的蓝线标出了将提取角度域成像道集的位置;图6c是提取CDP800处的方位一反射角成像道集,将方位角按照45°的间隔分成8个;图6d 是CDP1100处的方位-反射角道集,同样将方位角按照45°的间隔分成8个。对比图6a与图6b可以看出,高斯束偏移剖面的成像精度和成像信噪比较高,整体效果优于波动方程偏移结果,尤其在刻画能量较弱的地质目标体处的背斜界面同相轴更连续,成像效果更明显。这一点验证了前面介绍的高斯束优选偏移技术能够压制噪声的优势。而图6c的不同方位道集所显示出的成像同相轴拉平不一致现象也提示我们在后续研究中要开展方位各向异性研究。

高斯束偏移技术利用束优选来提高低信噪比资料的成像质量,并提取信噪比较高的角度道集,这有利于低信噪比实际资料成像剖面构造及成像道集剩余时差的自动拾取,对后续层析速度反演的实施具有重要意义。并且由于高斯束偏移技术很容易拓展应用到起伏地表偏移[19],因此,在复杂山前带资料成像中将发挥重要作用。但需要说明的是,高斯束偏移的实现仍然是基于高频近似的射线追踪,其所需的速度场一般需要平滑,因此,在诸如高精度的“串珠”型小缝洞成像以及高速体盐丘下边界成像方面,高斯束偏移的成像质量不如基于双程波动方程的逆时偏移。因此,根据高斯束偏移及其提取的角度道集的特点和应用条件来选择相应的实际资料进行应用显得很有必要。

图6　中国南方某实际数据高斯束偏移提取方位-反射角道集a 单程波叠前深度偏移某inline线剖面;b相同inline线高斯束叠前深度偏移剖面;c CDP800处(蓝线所示)的方位-反射角道集(方位角间隔45°,共分为8个,反射张角范围是0～60°); d CDP1100处(蓝线所示)的方位-反射角道集(方位角间隔45°,共分为8个,反射张角范围是0～60°)

4结束语

高斯束偏移的基本特点是沿射线中心坐标系进行傍轴近似方程的波传播。高斯束偏移利用相互独立的高斯束叠加并成像,解决了射线类方法中的多路径问题,因此,高斯束偏移兼具了射线理论和波动理论的优势。高斯束函数可以解析地计算得到波场传播的慢度矢量,从而在高斯束叠前深度偏移中方便地提取方位-反射角成像道集。利用高斯束偏移方法提取方位-反射角道集精度较高、计算稳定且额外增加的计算量较小。该道集可用于角度域的层析速度分析等后续处理。在高斯束传播之前对平面波分解进行数据“优选”可以明显改进成像信噪比。理论模型和实际资料的试算结果证明高斯束深度偏移是一种准确而有效的地震成像方法。

参考文献

[1]ALKHALIFAH T,FOMEL S.Angle gathers in wave-equation imaging for transversely isotropic media[J].Geophysical Prospecting,2011,59(3)：422-431

[2]AUDEBERT F,FROIDEVAUX P,RACOTOARISOA H,et al.Insights into migration in the angle domain[J].Expanded Abstracts of 72ndAnnual Internat SEG Mtg,2002:1188-1191

[3]BIONDI B,TISSERANT T.3D angle-domain common-image gathers for migration velocity analysis[J].Geophysical Prospecting,2004,52(6):575-591

[4]BIONDI B.Angle-domain common-image gathers from anisotropic migration[J].Geophysics,2007,72(2):S81-S91

[5]BRANDSBERG-DAHL S,DE HOOP M V,Ursin B.Focusing in dip and AVA compensation on scattering-angle/azimuth common image gathers[J].Geophysics,2003,68(2):232-254

[6]CHENG J B,WANG T F,WANG C L,et al.Azimuth-preserved local angle-domain prestack time migration in isotropic,vertical transversely isotropic and azimuthally anisotropic media[J].Geophysics,2012,77(1):S15-S27

[7]KOREN Z,RAVVE I,RAGOZA E,et al.Full azimuth angle domain imaging[J].Expanded Abstracts of 78thAnnual Internat SEG Mtg,2008:2221-2225

[8]PRUCHA M,BIONDI B,SYMES W.Angle-domain common image gathers by wave-equation migration[J].Expanded Abstracts of 69thAnnual Internat SEG Mtg,1999:824-827

[9]RICKETT J,SAVA P.Offset and angle-domain common image point gathers for shot-profile migration[J].Geophysics,2002,67(2):883-889

[10]SAVA P,FOMEL S.Angle-domain common image gathers by wavefield continuation methods[J].Geophysics,2003,68(2):1065-1074

[11]SAVA P,FOMEL S.Coordinate-independent angle-gathers for wave equation migration[J].Expanded Abstracts of 75thAnnual Internat SEG Mtg,2005:2052-2055

[12]SAVA P,VLAD I.Wide-azimuth angle gathers for wave-equation migration[J].Geophysics,2011,76(3):S131-S141

[13]GRAY S H.Angle gathers for gaussian beam migration [J].Expanded Abstracts of 69thEAGE Annual Conference,2007:C018

[14]XIE X B,WU R S.Extracting angle domain information from migrated wavefield[J].Expanded Abstracts of 72ndAnnual Internat SEG Mtg,2002:1360-1363

[15]XU S,CHAURIS H,LAMBARÉ G,et al.Common angle image gather:a new strategy for imaging complex media[J].Expanded Abstracts of 68thAnnual Internat SEG Mtg,1998:1538-1541

[16]XU S,CHAURIS H,LAMBARÉ G,et al.Common-angle migration:a strategy for imaging complex media[J].Geophysics,2001,66(3):1877-1894

[17]XU S,ZHANG Y,TANG B.3D common image gathers from reverse time migration[J].Expanded Abstracts of 80thAnnual Internat SEG Mtg,2010:3257-3260

[18]ZHANG Y,XU S,BLEISTEIN N,et al.True-amplitude,angle domain,common-image gathers from one-way wave-equation migrations[J].Geophysics,2007,72(1):S49-S58

[19]蔡杰雄,方伍宝,王华忠,等.高斯束深度偏移的实现与应用研究[J].石油物探,2012,51(5)：119-125

CAI J X,FANG W B,WANG H Z,et al.Realization and application of Gaussian beam depth migration[J].Geophysical Prospecting for Petroleum,2012,51(5):119-125

[20]李振春,岳玉波,郭朝斌,等,高斯波束共角度保幅深度偏移[J].石油地球物理勘探,2010,45(3)：360-365

LI Z C,YUE Y B,GUO C B,et al.Gaussian beam common angle preserved-amplitude migration[J].Oil Geophysical Prospecting,2010,45(3):360-365

[21]ALKHALIFAH T.Gaussian beam depth migration for anisotropic media[J].Geophysics,1995,60(1):1474 -1484

[22]POPOV M M,SEMTCHENOK N M,VERDEL A R,et al.Seismic depth migration with Gaussian beams[J].Expanded Abstracts of 69thEAGE Annual Conference,2007:P173

[23]POPOV M M,SEMTCHENOK N M,VERDEL A R,et al.Reverse time migration with Gaussian beams and velocity analysis applications[J].Expanded Abstracts of 70thEAGE Annual Conference,2008:F048

[24]POPOV M M,SEMTCHENOK N M,POPOV P M,et al.Depth migration by the Gaussian beam summation method[J].Geophysics,2010,75(2):S81-S93

[25]HILL N R.Gaussian beam migration[J].Geophysics,1990,55(11):1416-1428

[26]HILL N R.Prestack Gaussian beam depth migration[J].Geophysics,2001,66(4):1240-1250

(编辑：顾石庆)

Azimuth-opening angle domain common-image gathers from 3D Gaussian beam migration

CAI Jiexiong1,2,WANG Huazhong2,WANG Lixin1

(1.WavePhenomenaandInversionImagingResearchGroup(WPI),SchoolofOcean&EarthScience,TongjiUniversity,Shanghai200092,China; 2.SinopecGeophysicalResearchInstitute,Nanjing211103,China)

Abstract:Common-image gathers indexed by opening angle and azimuth at imaging point in 3D situation are key input for amplitude versus azimuth (AVA) analysis and traveltime velocity tomography.The Gaussian beam depth migration (GBM),propagating a beam along each ray and summing the contributions from all the individual beams to produce the wavefield,can overcome the multipath problem,image steep reflectors and more importantly provide a convenient and efficient strategy to extract azimuth-opening angle domain common-image gathers (ADCIGs) in 3D seismic imaging.We present a method for computing azimuth and opening angle at imaging point to output 3D ADCIGs by computing the Gaussian beams wavefield direction vectors,which are solved analytically from Gaussian beam function.Numerical tests and field data application demonstrate the exaction method of ADCIGs from 3D Gaussian beam depth migration is effective.

Keywords:azimuth-opening angle domain common-image gathers (ADCIGs),Gaussian beam migration,ray tracing

文章编号：1000-1441(2016)01-0076-08

DOI:10.3969/j.issn.1000-1441.2016.01.010

中图分类号：P631

文献标识码：A

基金项目：国家科技重大专项(2011ZX05014-001-002)项目资助。

作者简介：蔡杰雄(1983—),男,博士在读,工程师,主要从事地震波反演与成像方法研究工作。

收稿日期：2015-02-08;改回日期：2015-05-13。

蔡杰雄,王华忠,王立歆.基于三维高斯束算子解析的方位-反射角道集提取技术研究[J].石油物探,2016,55(1):-83

CAI Jiexiong,WANG Huazhong,WANG Lixin.Azimuth-opening angle domain common-image gathers from 3D Gaussian beam migration[J].Geophysical Prospecting for Petroleum,2016,55(1):-83

This research is financially supported by the National Science and Technology Major Project of China (Grant No.2011ZX05014-001-002).