f-x域经验模式分解与多道奇异谱分析相结合去除随机噪声

刘婷婷,陈阳康

(1.中国石油化工股份有限公司上海油气分公司研究院,上海200120;2.德克萨斯大学奥斯汀分校,德克萨斯州奥斯汀TX73301)



f-x域经验模式分解与多道奇异谱分析相结合去除随机噪声

刘婷婷1,陈阳康2

(1.中国石油化工股份有限公司上海油气分公司研究院,上海200120;2.德克萨斯大学奥斯汀分校,德克萨斯州奥斯汀TX73301)

摘要:近年来,经验模式分解法(EMD)因其处理非稳态地震信号的能力和易于实现而备受关注。总结了EMD在地震去噪中的应用情况,提出了一种基于f-x域EMD和多道奇异谱分析(MSSA)相结合的去噪新方法。该方法不同于f-x域EMD分别与f-x域预测滤波、小波阈值、曲波变换等相结合的各种去噪方法,它可以得到比f-x域MSSA更高的信噪比并能预测f-x域EMD中损失掉的线性能量。该方法的实现过程为:首先,对地震剖面应用f-x域EMD,保留所有相对水平的同相轴,这样在噪声剖面中留下很少的倾斜信号和随机噪声,然后在差异剖面中应用f-x域MSSA恢复倾斜信号,最后将水平信号和倾斜信号相加得到去噪剖面。理论测试和实际数据的处理结果验证了该方法的优越性。

关键词:去除随机噪声;经验模式分解法;多道奇异谱分析法;f-x域;恢复倾斜同相轴

非常规能源勘探的快速发展对地震资料叠前和叠后的处理提出了更高的要求。噪声干扰将导致在地震资料处理过程中产生诸多误差,常使得最终的叠加剖面出现构造假象或层位不清晰等异常现象,噪声衰减是将噪声从地震资料中剔除,滤出有效信号,提高资料信噪比。目前存在的随机噪声压制技术主要可以分为4类：第1类是基于有效信号的可预测性,如:CANALES等[1]、赵德斌等[2]、CHEN等[3]、康冶等[4]提出的f-x域预测滤波,Liu等[5]提出的f-x非稳态预测滤波;第2类是基于地震同相轴的统计特征,如:HUO等[6]提出的均值滤波、中值滤波;第3类是基于地震数据的主成分分析法,如:OROPEZA等[7]提出的多道奇异谱分析(MSSA);第4类是GAO等[8]、NEELAMANI等[9]和FOMEL等[10]提出的基于变换域阈值法。

HUANG等[11]提出了一种新的信号处理方法,把信号进行经验模式分解(EMD)后作为Hilbert变换的输入。EMD的本质是使非稳态信号平稳化,也就是说,把一个信号分解为一系列固有模态函数(IMF),每一个IMF的局部频率相对为常数,每一个IMF的频率随着IMF被分解的次序而降低。EMD是分析线性和稳态谱的突破性技术,自适应地将地震数据的非线性和非稳态信号特征分解到不同频段范围中。BEKARA等[12]把f-x域EMD应用于地震数据随机噪声的去除,理论测试和实际应用证明了此方法比f-x预测滤波效果好。近年来,基于EMD与其它方法结合去噪法备受关注[3,13-15]。CHEN等[3]注意到f-x域EMD在处理复杂构造时的问题,提出f-x域EMD预测滤波(EMDPF),这个方法结合了f-x域EMD和f-x预测滤波的优点。集合经验模式分解法(EEMD)是EMD的改进方法,CHEN等[14]把EEMD与小波阈值相结合,得到更好的去噪结果。同样地,DONG等[15]把f-x域EMD与曲波阈值相结合,比单独使用去噪效果更好[14]。由于f-x域EMD对于保留水平同相轴相对于其它方法的无可替代性,越来越多的人提出将f-x域EMD与其它方法相结合来去除噪声[15]。

本文中,我们提出了f-x域EMD和MSSA相结合的去除随机噪声的总体框架,相对于f-x域EMD保留了小的倾斜构造;相对于f-x域MSSA提高了去除噪声后剖面的信噪比。合成地震记录理论测试和实际资料应用结果验证了本文方法的优越性。

1方法原理

1.1经验模式分解法(EMD)

EMD的目的是利用经验方法把一个非稳态信号分解为一系列有限个数的子信号,也就是说经验模态函数IMF可以看作是稳态的。IMF满足两个条件:①在整个数据内,极值和0值的个数相等或者至多差一个;②在任何点,由局部极大值和局部极小值定义的包络的均值为0[11]。

给定s(t),c(t),r(t)和n,它们分别代表原始非稳态信号、分解得到的IMF、余量、IMF的个数,那么EMD的数学原理可以表示为:

(1)

对于一个非稳态信号s(t),通过方程(1),我们可以得到有限个cn(t),n=1,2,…,N。

EMD的一个特殊的属性就是IMF代表原始数据中不同的振荡成分,每一个子信号cn(t)的振荡频率随着IMF被分解的次序逐渐降低。

图1和图2给出了非稳态信号EMD的实例。图1为非稳态信号和相应的瞬时频率。通过瞬时频率可以看出原始信号可以被分为4个部分。在0～6.0s,信号由3个频率成分组成,分别为5,15,33Hz;在6.0～7.8s,信号由2个频率成分组成,分别为10Hz和33Hz;在7.8～9.0s,是一个单一成分的信号,频率是10Hz;在9.0～14.0s,信号由2个频率成分组成,分别为5Hz和15Hz;最后,14.0～15.0s,信号由3个频率成分组成,分别为5,15,34Hz。图2为对该合成信号进行EMD分解得到的各个IMF分量,可以看出,不同频率的信号成分被分解开来,在IMF分量中得以体现,并且和瞬时频率一致,伴有微弱的边界效应。

1.2f-x域EMD

图1　非稳态信号(a)和相应的瞬时频率(b)

图2　EMD分解后各IMF分量a 第1个IMF分量; b 第2个IMF分量; c 第3个IMF分量; d 余量

BEKARA等[12]提出f-x域EMD用来去除随机噪声[13],他们把EMD应用到f-x域数据的每一个频率切片上,去除第1个IMF分量,其主要代表高波数分量即随机噪声。这个方法可以总结为:

(2)

1) 选取时窗,将时窗内的数据通过短时傅里叶变换到f-x域;

2) 对每一个频率,沿空间方向分别对实部和虚部序列进行EMD分解,去除第1个IMF分量;

3) 对处理后的IMF分量叠加后组成复信号,短时傅里叶变换到t-x域;

4) 移动到下一个时窗,重复步骤1)至步骤3)。

图3为对有效信号为水平同相轴的剖面应用f-x域EMD去噪效果。在每一个小图中,上图是20Hz频率切片的实数部分,下图是相应的合成剖面。图3a,图3b和图3c分别为无噪数据、含噪数据和所添加高斯噪声数据。从20Hz数据频率切片可以看到水平同相轴的波数为0。在对含噪数据进行f-x域EMD后,每一个频率切片移除4个IMF分量得到噪声数据和去除噪声后的数据，结果如图3c和图3d所示,可以看到,去除噪声后剖面非常干净,它对应的20Hz频率切片基本为常数,在噪声剖面中,没有相干能量,其频率切片的谱与高斯噪声谱吻合,验证了该方法去除随机噪声的有效性。

当有效信号为倾斜同相轴时,f-x域EMD不再有好的去噪结果(图4)。图4a,图4b,图4c分别为无噪剖面、添加的随机噪声和含噪剖面。从图4a 中的f-x域频率切片可以看出,倾斜同相轴对应的20Hz频率切片为一正弦曲线。我们比较了去除不同IMF分量的效果。图4d,图4e和图4f分别为去除前1,2,3个IMF分量的去噪效果,图4g,图4h和图4i分别为对应的噪声剖面。很明显,去除第1个IMF分量后,有用的倾斜信号大部分已经被损害;在去除前2个IMF分量后,有效能量大部分已经被去除;去除前3个IMF分量后,整个倾斜信号完全被去除。从频率切片曲线中同样可以看出,有效倾斜同相轴对应的正弦曲线大部分也被移除。对于地下复杂构造的信号,一个很大的问题就是f-x域EMD不再有效。

图3　有效信号为水平同相轴的剖面应用f-x域EMD的效果a 无噪数据; b 添加的随机噪声; c添加的高斯噪声数据; d 去除噪声后的剖面; e 差异剖面

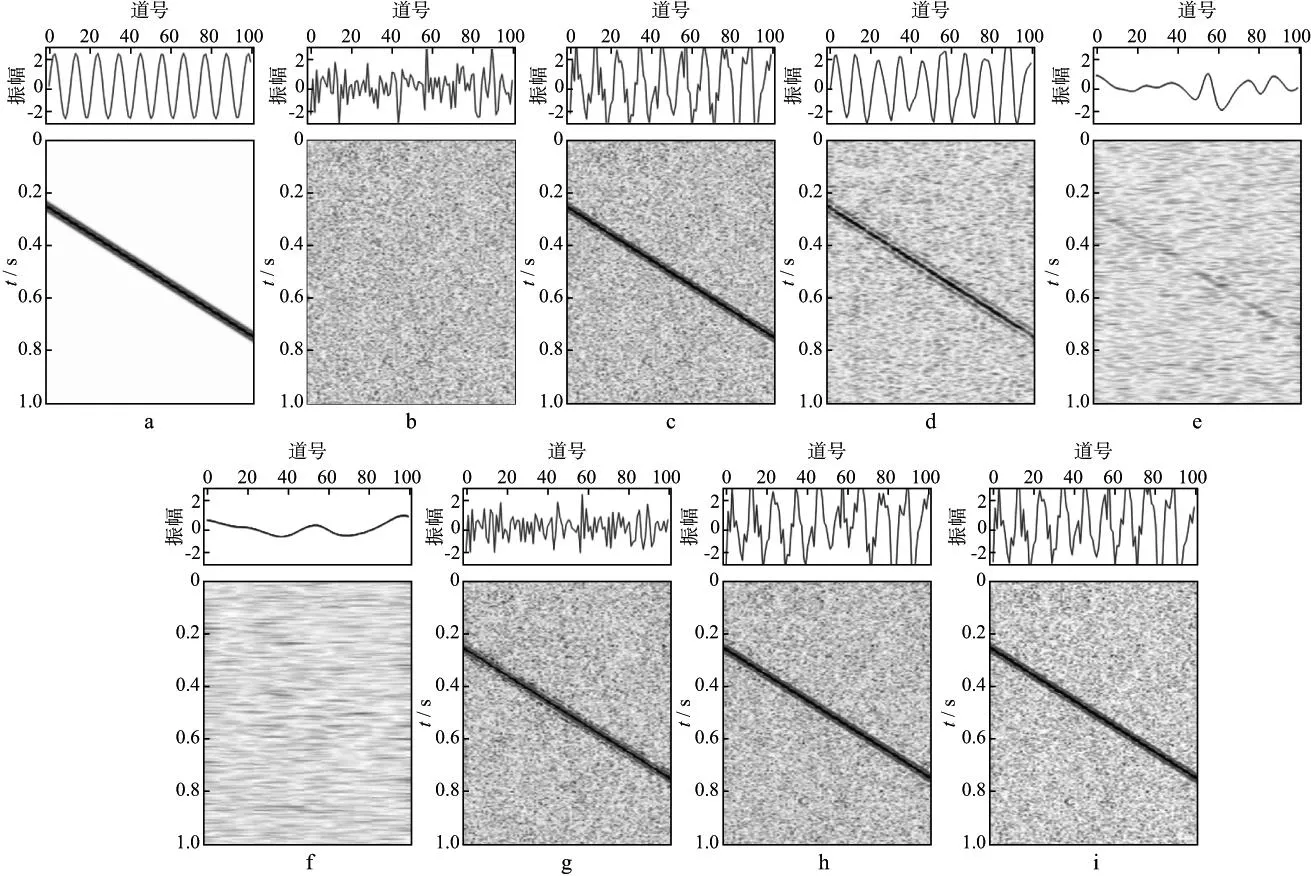
图4　有效信号为倾斜同相轴的剖面应用f-x域EMD的效果a 无噪数据; b 添加的随机噪声; c 含噪数据; d 去除第1个IMF分量的去噪剖面; e 去除前2个IMF分量的去噪剖面; f 去除前3个IMF分量的去噪剖面; g,h,i分别为对应d,e,f的差异剖面

1.3f-x域MSSA

考虑二维地震数据D(m,w),m=1,2,…,M,M为空间方向的道数，对每一个频率切片构造一个Hankel矩阵,有:

(3)

其中,

(4)

(5)

(4)式中,[·]代表整数部分。已经证明,对于无噪数据,若时间剖面有K个独立倾角的平面波,则这个Hankel矩阵的秩为K。加入随机噪声后,矩阵的秩会增加。所以,可以通过降秩来达到去除随机噪声的目的[8]。具体步骤如下：

1) 选取时窗,将时窗内的数据通过短时傅里叶变换到f-x域;

2) 对每一个频率数据,构造Hankel矩阵;

3) 对Hankel矩阵进行SVD分解,如果时窗内有K个同相轴,则保留前K个较大的奇异值,将其它置0,再重构得到低秩Hankel矩阵,对低秩Hankel矩阵反对角线取均值;

4) 移动到下一个时窗,重复步骤1)至步骤3)。

对于一个有少数平面波的含噪合成数据来说(图5),f-x域MSSA尤其有效,因为有效信号可以通过对Hankel矩阵降秩来捕捉到。图5为图4中数据去除噪声后的效果。去除噪声后信号的频谱与原始无噪信号非常接近,而且去除的噪声不包含任何相干信号,证明了f-x域MSSA的有效性。此时Hankel矩阵的秩由3降到了1。

1.4f-x域EMD&MSSA

(6)

(7)

这里,P是一个去噪算子,用来从噪声剖面中估计出损失的倾斜同相轴。最后,我们把水平和估计出的倾斜成分相加得到最终的去噪剖面,即:

(8)

新方法的有效性归功于f-x域EMD在保留水平同相轴方面相对于其它方法的无可替代性。水平同相轴对应的波数是0,有效的水平成分对应EMD分解过程中最后一步得到的趋势余量。在水平成分大部分都被保留下来的基础上,我们转向处理差异剖面中的小部分倾斜成分,对小部分倾斜同相轴来说更容易处理,能增强对随机噪声的衰减。例如,在f-x预测滤波中表现为更小的预测长度[2],在f-x域MSSA中表现为降秩降到更低[7]。这个方法可以用于叠后剖面和叠前共偏移距剖面,因为大部分地震信号是水平的。f-x域EMD损失的倾斜成分可以通过在目标区域应用f-x域MSSA恢复,而无需应用在整个剖面上。本方法的巧妙之处在于没有引入新的噪声。对于双曲共中心点道集,这个方法首先应用f-x域EMD去除足够的噪声,同时远炮检距的倾斜成分也会被去掉,然后在差异剖面中远炮检距的区域,应用f-x域MSSA来恢复有效信号。

图5　图4c所示数据应用f-x域MSSA的效果a 去除噪声后的剖面; b 差异剖面

2理论测试与实际应用

2.1理论数据测试

实例1中的合成剖面包括5条水平和2条倾斜交叉同相轴。测试中,我们使用40Hz雷克子波合成地震记录,采样间隔是2ms。图6为线性理论模型测试结果,从图6中可以看到,所含随机噪声能量非常强。图7为f-x域EMD,f-x域MSSA和本文方法去除噪声后的剖面效果对比。从图7d可以看出,尽管f-x域EMD去除了大部分随机噪声,但是有效倾斜同相轴同时被去除。从图7e可以看出,f-x域MSSA虽然保留了倾斜信号,但噪声去除不明显。比较3种方法的去噪效果可以看到,本文方法在保持有效信号的同时,最大程度地去除了噪声,并且适用于交叉同相轴剖面的去噪。可见,本方法适用于叠后数据的处理,既可以有效保留水平轴,也可以保留细节小构造；并且恢复倾斜信号时,只需对目标区域作处理,节约计算成本。

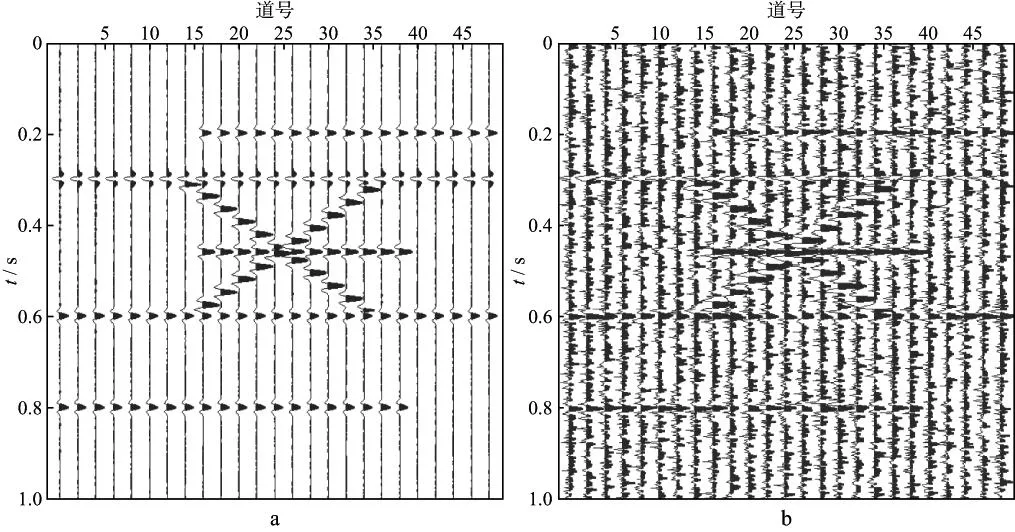
图6　线性理论模型测试结果a 无噪剖面; b 含噪剖面

图7　线性理论模型3种方法去噪效果对比a f-x域EMD; b f-x域MSSA; c 本文方法; d,e,f分别为a,b,c对应的差异剖面

实例2为模拟地震叠前记录,由1个直达波和2个双曲反射波组成。测试中,我们同样使用了40Hz雷克子波合成地震记录,采样间隔为2ms。图8为双曲理论模型测试结果。图9为3种方法的去噪效果对比。对于叠前数据去除随机噪声来说,应该在不损伤其它信号的基础上进行,直达波通常用来拾取浅层速度进行静校正,在西部山区、沙漠地带的常规地震数据处理中尤为重要,同时在微地震中,拾取初至是找到有效信号的关键步骤,通过f-x域EMD与f-x域MSSA相结合,可有效保留倾斜信号。本实例中,3种方法的效果有明显差异。f-x域EMD去噪后剖面更干净,但损失了直达波(图9a,图9d);f-x域MSSA在处理非线性信号时,采用分窗来克服理论中的同相轴线性假设,加之一个窗口内轴过多导致降秩选择的不明确性,造成去噪效果不理想(图9b,图9e)。从图9c和图9f中可以看出,本文方法用f-x域EMD保留了相对平缓的双曲反射波,同时利用f-x域MSSA恢复了少数倾斜同相轴,去噪效果比前两种方法的效果明显要好,虽然对于随机噪声的去除没有太大优势,但是对于有效信号的保留非常有效,适用于叠前地震数据和微地震数据的去噪处理。

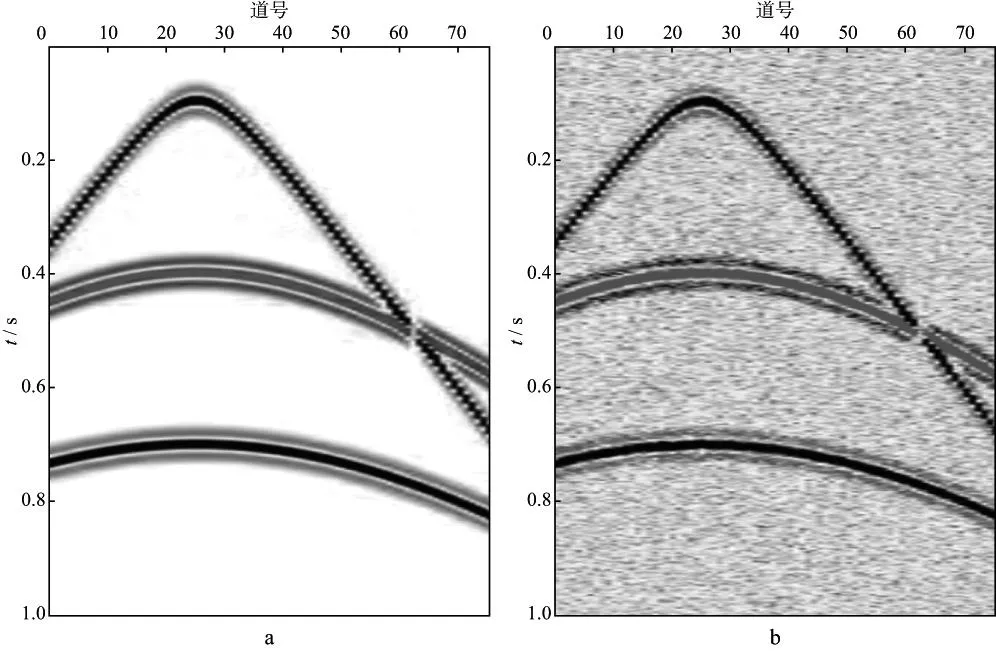
图8　双曲理论模型测试a 无噪剖面; b 含噪剖面

图9　双曲理论模型3种方法去噪效果对比a f-x域EMD; b f-x域MSSA; c 本文方法; d,e,f分别为a,b,c对应的差异剖面

为了量化比较不同方法的去噪效果,我们应用了一种之前被使用过的衡量方法[5],即:

(9)

2.2实际资料应用

图10是一个多分量P波剖面。可以看出,地震剖面中噪声在浅层部分能量尤其强,对随机噪声的去除提出了更高的要求。图11为3种方法的去噪效果。原始数据中大部分信号是水平的,所以f-x域EMD是首选方法,但从图11d可以看出,f-x域EMD会丢失部分细节信息。本文方法和f-x域MSSA看起来没太大区别,但是详细分析方法剖面中A区域发现,本文方法的去噪更干净。从B区域可以看出,本文方法可以更好地保持地震剖面中的细节部分。图12为图11中A区域的放大显示。

图10　原始数据

表1　不同方法去噪后的信噪比

图11　不同方法去噪效果比较a f-x域EMD; b f-x域MSSA; c 本文方法; d,e,f分别为a,b,c对应的差异剖面

图12　f-x域MSSA(a)和本文方法(b)的去噪效果对比(图11中A区域放大显示)

3结束语

我们提出了一种将f-x域EMD和MSSA相结合的去噪方法。本文方法解决了f-x域EMD损失倾斜信号的问题,同时提高了f-x域MSSA的信噪比,此外还解决了在处理非线性、同相轴交叉、构造复杂等情况下严重损害有效信号的问题。本文方法巧妙地利用了EMD对于保持水平信号的无可替代性,同时利用f-x域MSSA来恢复有效倾斜成分。从实例应用效果来看,本文方法可以得到比f-x域MSSA更高的信噪比,同时可以保持f-x域EMD中损失掉的倾斜成分。通过调整参数,本文可同时适合于叠前、叠后数据随机噪声的去除,实际应用潜力大、前景广阔。

参考文献

[1]CANALES L.Random noise reduction[J].Expanded Abstracts of 54thAnnual Internat SEG Mtg,1984:525-527

[2]赵德斌,黄真萍,王春梅.f-x域奇异值分解预测滤波法随机噪声衰减[J].石油物探,1998,37(3):29-33

ZHAO D B,HUANG Z P,WANG C M.Random noise attenuation using predictive filtering inf-xdomain by singular value decomposition[J].Geophysical Prospecting for Petroleum,1998,37(3):29-33

[3]CHEN Y,MA J.Random noise attenuation byf-xemprical mode decomposition prediction filtering[J].Expanded Abstracts of 83rdAnnual Internat SEG Mtg,2013:4340-4346

[4]康冶,于成业,贾卧,等.f-x域去噪方法研究[J].石油地球物理勘探,2003,38(2):136-138

KANG Y,YU C Y,JIA W,et al.Institute of exploration & development[J].Oil Geophysical Prospecting,2003,38(2):136-138

[5]LIU G,CHEN X,DU J,et al.Seismic noise attenuation using nonstationary polynomial fitting[J].Applied Geophysics,2011,8(1):18-26

[6]HUO S,LUO Y,KELAMIS P G.Simultaneous sources separation via multidirectional vector-median filtering[J].Geophysics,2012,77(4):V123-V131

[7]OROPEZAV,SACCHI M.Simultaneous seismic data denoising and reconstruction via multichannel singular spectrum analysis[J].Geophysics,2011,76(3):V25-V32

[8]GAO J,MAO J,CHEN W,et al.On the denoising method of prestack seismic data in wavelet domain[J].Chinese Journal of Geophysics,2006,49(4):1155-1163

[9]NEELAMANI R,BAUMSTEIN A,GILLARD D,et al.Coherent and random noise attenuation using the curvelet transform[J].The Leading Edge,2008,27(2):240-248

[10]FOMEL S,LIU Y.Seislet transform and seislet frame[J].Geophysics,2010,75(3):V25-V38

[11]HUANG N E,SHEN Z,LONG S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Royal Society of London Proceedings,1998,454(1971):903-995

[12]BEKARA M,VAN DER BAAN M.Random and coherent noise attenuation by empirical mode decomposition [J].Geophysics,2009,74(5):V89-V98

[13]王维强,杨国权.基于EMD与ICA的地震信号去噪技术研究[J].石油物探,2012,51(1):19-29

WANG W Q,YANG G Q.Seismic data noise attenuation technology based on EMD and ICA[J].Geophysical Prospecting for Petroleum,2012,51(1):19-29

[14]CHEN W,WANG S,ZHANG Z,et al.Noise reduction based on wavelet threshold filtering and ensemble empirical mode [J].Expanded Abstracts of 82ndAnnual Internat SEG Mtg,2012:1-6

[15]DONG L,LI Z,WANG D.Curvelet threshold denoising joint with empirical mode decomposition[J].Expanded Abstracts of 83rdAnnual Internat SEG Mtg,2013:4412-4416

(编辑:顾石庆)

Random noise attenuation based on EMD and MSSA inf-xdomain

LIU Tingting1,CHEN Yangkang2

(1.ShanghaiOffshoreOil&GasCompany,SINOPEC,Shanghai200120,China;2.UniversityofTexasatAustin,AustinTX73301,USA)

Abstract:In recent years,empirical mode decomposition (EMD) has gotten a lot of public attention due to its capability in processing non-stationary seismic signal and its convenience to implement.In this paper,we summarized the existing applications of EMD in seismic data denoising,and proposed a new approach combining EMD in f-x domain and multi-channel singular spectrum analysis (MSSA) to attenuate random noise.Comparing those approaches combining f-x EMD with other methods such as prediction filtering in f-x domain,wavelet threshold and curvelet transformation,the new approach can obtain higher SNR compared to f-x MSSA and can predict the lost linear energy due to f-x EMD.The workflow of the method is as follows:implementing f-x EMD to the given seismic data at first,all the relative horizontal events can be retained,leaving part of useful dipping signals and some random noises in the difference profile;then f-x MSSA can be used in the difference profile to restore dipping signals;finally resultful profile can be gotlen by horizontal signals plus dipping signals.Two synthetic and a real data examples demonstrate the superiority of the proposed approach.

Keywords:random noise attenuation,empirical mode decomposition (EMD),multi-channel singular spectrum analysis (MSSA),f-x domain,dipping event restoration

文章编号:1000-1441(2016)01-0067-09

DOI:10.3969/j.issn.1000-1441.2016.01.009

中图分类号:P631

文献标识码:A

作者简介:刘婷婷(1989—),硕士,助理工程师,主要研究方向为地震资料处理、反演方法研究。

收稿日期:2015-01-21;改回日期:2015-07-28。

刘婷婷,陈阳康.f-x域经验模式分解与多道奇异谱分析相结合去除随机噪声[J].石油物探,2016,55(1):-75

LIU Tingting,CHEN Yangkang.Random noise attenuation based on EMD and MSSA inf-xdomain[J].Geophysical Prospecting for Petroleum,2016,55(1):-75